小样本不平衡设备数据下的机器学习策略研究

陈 扬，刘勤明，梁耀旭

（上海理工大学 管理学院，上海 200093）

随着我国科技水平的飞速发展，我国对设备的健康寿命预测准确度要求越来越高，很多关键设备一旦在服役期间出现事故很有可能会造成大量人员伤亡或巨大经济损失[1]。因此，及时准确地检查出设备的健康状况问题至关重要。

随着机器学习和深度学习的飞速发展，越来越多的人工智能技术开始普及。其中，机器学习中的代表算法支持向量机(support vector machine,SVM)、神经网络(neural networks,NNs)、随机森林(random forests,RF)和K 邻近值算法被越来越多地运用到实际工业生产中。在机器学习与深度学习算法的实际应用方面，刘文溢等[2]提出了一种基于隐马尔可夫链的设备寿命预测模型，并通过算例验证了该算法在实际工业寿命预测领域的可行性。曹正志等[3]提出卷积神经网络与双向长短期记忆网络相结合预测设备健康数据特征发展趋势，并通过实验证明了该方法的有效性。但是，现阶段越来越多的算法只面向大规模数据，在小样本不平衡数据下很多算法不再适用，因此，发展面向小样本不平衡数据的算法存在必要性[4]。

SMOTE (synthetic minority oversampling technique)算法是目前适用较多的合成少数类过采样技术，它是基于随机过采样算法的一种改进方案。由于随机过采样采取简单复制样本的策略来增加少数类样本，这样容易产生模型过拟合的问题，即使得模型学习到的信息过于特别而不够泛化。SMOTE 算法的基本思想是对少数类样本进行分析，并根据少数类样本人工合成新样本添加到数据集中。SMOTE 算法本身也存在很多问题，首先邻近值的选择难以确定，同时面对异常值以及不平衡数据分布的时候表现并不理想。针对以上问题，Han 等[5]提出了一种Borderline-SMOTE 算法，目前这也是最广为人接受的改进算法。杨赛华等[6]在此基础上提出了一种BN-SMOTE 改进算法，利用最近邻思想构建处于决策边界附近的多数类样本集，再一次确定边界区域难以学习的少数类样本点从而构建一个新的少数类样本集。杨毅等[7]在Han 的研究基础上提出了一种RB-SMOTE 的改进模型，通过合成不平衡率不一的多个新训练样本，组成相应的多个基分类器，再采用投票的方式对测试样本进行分类。Bansal 等[8]提出了SMOTE-M算法规避数据不平衡带来的问题。王超学等[9]提出了一种GA-SMOTE 算法提高SMOTE 面对不平衡数据集的分类性能。以上几种算法均对SMOTE 算法进行不同程度的改进，但是，面对多数类样本中存在的噪声的问题并没有进行有效处理，因此，以上几种改进算法并不能很好地对已有数据进行优化。

在此基础上，面对存在问题的数据，传统KNN 算法也无法处理不平衡数据和噪声问题，因此，不能直接应用于大多数情况下的设备寿命数据处理。同时，当不同种类样本点分布较为紧密时，KNN 算法难以对数据进行有效分类。针对此情况，本文提出了一种ISMOTE 算法(Improvement-SMOTE)，通过改进SMOTE 算法克服了传统SMOTE 算法存在的问题，使得改进后的新增数据不再出现边缘化、存在异常值、分类结果不够泛化等弊端。由于传统KNN 算法无法面向小样本不平衡以及存在异常值的数据，利用ISMOTE 算法改进后的数据刚好可以弥补KNN 算法的不足，使得KNN 算法可以应用在存在小样本不平衡数据的设备寿命预测领域。其次，在实际工业生产中，出现问题的数据有时会和正常设备的数据紧密分布，当不同种类的数据分布较为紧密时，KNN 算法的分类效果并不好。针对此问题，本文提出了一种投票式KNN (Voting-KNN,VKNN)算法。根据测试集数据分布以及数据种类引入PSO(particle swarm optimization)寻求每个设备状态数据分布的中心点，随后通过计算同簇样本点到中心点的欧式距离均值建立分隔阈值，对到中心点距离小于的数据点利用“投票法”判断数据种类，抛弃传统KNN 算法计算k个距离最近样本点从而判断样本种类的法则，规避数据混淆引起的误差。优化后的数据通过改进KNN 算法在准确分析设备健康状态的同时也可以有效预测设备未来健康发展趋势。

1 问题描述

目前机器学习领域越来越多的算法只适用于面向大量有效数据的情况。而面向小样本不平衡数据，误用传统机器学习算法很有可能会导致人们对设备的寿命产生错误预测从而造成巨大的经济损失[10]，因此，在数据不足的情况下可以通过数据增强提高样本质量[11]。面对传统KNN 算法无法处理不平衡和异常数据的情况，本文采用改进SMOTE 算法（ISMOTE）。ISMOTE 算法首先对数据进行新增处理，采用类似k邻近值原理剔除分布较为分散的异常数据，在保持数据特征的前提下人工合成符合条件的数据，解决了传统SMOTE算法新增样本出现新增样本点质量低、容易边界模糊以及新增后数据分布出现异常的问题。最后，通过VKNN 算法对优化数据进行分类，模型如图1 所示。

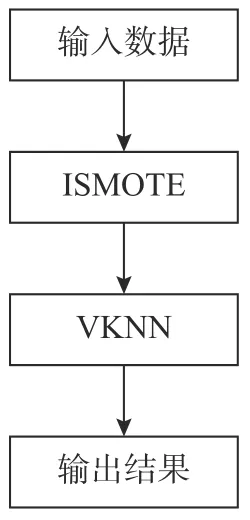
图1 基于ISMOTE-VKNN 模型的设备数据分析流程Fig.1 Equipment data analysis process based on the ISMOTE-VKNN model

2 改进SMOTE 算法

2.1 面向不平衡分类问题的SMOTE 算法

SMOTE 即合成少数类过采样技术[12]，它是基于随机过采样算法的一种改进方案。由于随机过采样采取简单复制样本的策略来增加少数类样本，SMOTE 算法的基本思想是对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中，算法流程如下：

a.对于少数类中每一个样本x，以欧氏距离为标准计算它到少数类样本集中所有样本的距离，得到其k个近邻。

b.根据样本不平衡比例设置一个采样比例以确定采样倍率N，对于每一个少数类样本x，从其k个近邻中随机选择若干个样本，假设选择的近邻为xn。

c.对于每一个随机选出的近邻xn，分别与原样本按照如下的公式构建新的样本。

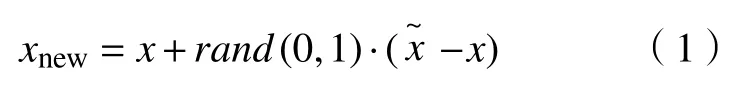
很显然，由于设备会受到运行环境以及状况等一系列条件的影响，从设备中提取的数据可能并不能直接用于SMOTE 算法进行优化。传统SMOTE 算法存在很多局限性，根样本或辅助样本中存在噪声可能会导致新增样本出现质量问题。在特殊情况下新增样本处于多数类与少数类样本的边界区域会导致数据集出现边界模糊的情况，而在此情况下使用传统SMOTE 算法同样会加重原先就存在的问题。因此，本文提出了一种改进SMOTE（ISMOTE）算法，该改进算法可以对以上问题进行规避，从而可以在数据存在问题的情况下对设备健康状况进行评估。

2.2 ISMOTE 算法

面对存在异常值点，也就是噪声的问题。这里的噪声是指出现在多数类样本群中的孤立的少数类样本，在设备数据方面表现为数据看起来正常但是实际上已经因为某些原因无法正常运行的那一类。针对这种情况，本文选择设置噪声比例β对每个少数点进行评估。噪声比例β的表达式为

式中：NMin为k邻近值中少数类样本个数；NMaj为多数类样本个数。

设置噪声标准α，x为 样本集。

若β＞α，按照如下公式构建新样本：

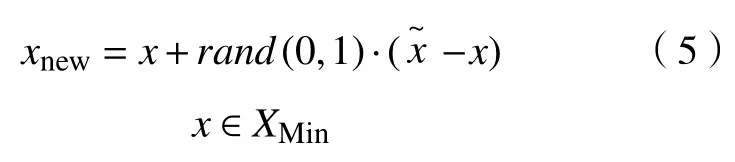
否则删除该样本点。

该改进法则的核心思想为通过噪声比例判断某种类样本集中是否出现一定数量的其他种类样本，如果出现频率低于所设置的阈值，则将那些出现的点视为噪声并删除。此过程是在保留样本分布特征的情况下对数据集进行优化，并不会影响后续步骤。

而当设备数据中正常数据与异常数据过于接近的情况发生的时候，针对传统SMOTE 算法中可能出现的边界模糊的情况，本文通过计算每个少数类样本点与周围最近的多数类样本点的欧式距离，通过与设置的阈值进行比较从而选择性地对部分少数类样本点进行新增样本的处理，欧氏距离的表达式为

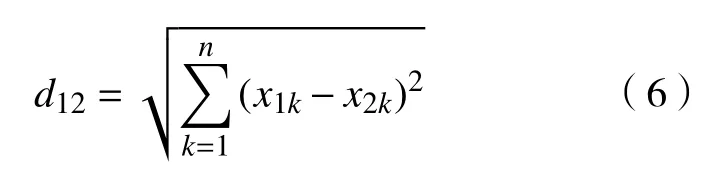
该改进算法不仅仅能处理二维数据，针对以多分类为目标的问题也可以优化多维数据集。

为了防止少数类样本点和多数类样本点在新增过程中分布过于接近，需要设置阈值dmin，这里设样本点计算出的实际距离为d。

设d＜dmin的样本点集为xi，则剩下的样本点集为

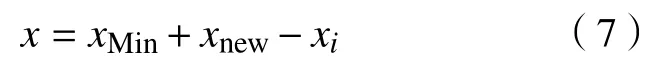
同样地，在特殊情况下多数类样本和少数类样本本身的分布可能就存在问题，即健康的设备数据和不健康的设备数据总是杂糅或是过于稀疏，这也会直接导致优化后的新增数据不够泛化。部分区域过于密集或是过于稀疏都会导致新增样本之后加重本身就存在的问题。一旦在这种情况下强行利用SMOTE 算法进行新增处理可能会导致最后利用机器学习算法分类时候准确性不足。因此，可以采用类似B-SMOTE 算法进行处理。

本文根据Han 提出的Borderline-SMOTE 算法的启发采用如下算法进行处理，这里计算少数类样本与周围同类k邻近值的距离d并通过设置阈值m进行比较。根据比较的结果数量将样本点分为以下几类：

设样本点x∈xMin

a.若对于任意x，都有d＜m，则x=xn

b.若对于任意x，至多50%样本的d＜m，则x=xh，从中随机抽取部分样本点xi进行新增处理，xi∈xh，抽取比例为25%～50%

c.若对于任意x，大于50%样本的d＞m，则x=xu，采用传统SMOTE 算法新增样本。

随后按照以下步骤对不同样本种类的样本点x进行处理:

忽略xn，

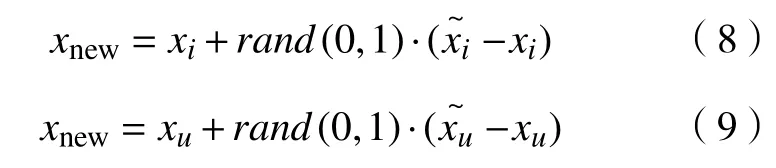
利用此方法可以解决数据本身存在的分布不均匀问题，同时将此方法与上述方法进行结合可以有效地对原本存在诸多问题的数据进行处理，将其变为可以被KNN 算法进行运算的数据。同时，优化后的数据可以规避传统KNN 算法中可能带来的种种问题。

ISMOTE 算法流程如图2 所示。

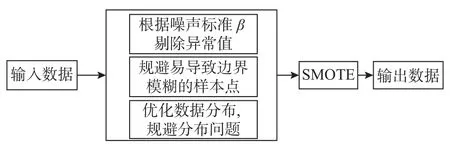
图2 ISMOTE 算法流程图Fig.2 Flow chart of ISMOTE algorithm

该改进算法不仅最大程度保留了样本集的分布特征，同时也在删除噪声、消除边界模糊、优化少数类样本分布方面对数据集进行了一定程度的优化，弥补了传统SMOTE 与B-SMOTE 的不足，使得经过该算法优化处理后的数据能够被目前大部分机器学习算法计算。

3 VKNN 算法

3.1 KNN 算法分析

KNN（K-Nearest Neighbor）法即k最邻近法，最初由 Cover 和Hart 于1968 年提出，是一个理论上比较成熟的方法，也是最简单的机器学习算法之一。该方法的思路非常简单直观：如果一个样本在特征空间中的k个最相似（即特征空间中最邻近）的样本中的大多数属于某一个类别，则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN 算法的核心思想是，如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。KNN 方法在类别决策时，只与极少量的相邻样本有关。

在KNN 算法理论方面，Yadav 等[13]比较了KNN 算法与其他机器学习算法在处理分类问题时的准确度，并从数学角度证明了KNN 算法拥有不错的分类能力。Xu 等[14]将KNN 与超球结构相结合，使得改进后的KNN-MVHM 算法能有效处理不均衡数据，规避了传统KNN 算法的局限性。殷小舟[15]针对支持向量机超平面附近的测试样本分类错误的问题，改进了将支持向量机分类和k近邻分类相结合的方法，形成了一种新的分类器。在分类阶段计算待识别样本和最优分类超平面的距离时，如果距离差大于给定阈值，可直接应用支持向量机分类，否则用最佳距离k近邻分类。李欢等[16]提出了一种有效的k近邻分类文本分类算法，即SPSOKNN 算法，该算法利用粒子群优化方法的随机搜索能力在训练集中随机搜索，在搜索k近邻的过程中，粒子群跳跃式移动，掠过大量不可能成为k近邻的文档向量，并且去除了粒子群进化过程中粒子速度的影响，从而可以更快速地找到测试样本的k个近邻。以上算法都对KNN 算法进行了改进，提高了分类精度以及分类速率，但是却没有解决KNN 算法数据分布重叠导致分类误差较大以及无法面向不平衡数据的问题，因此，上述算法在预测设备健康状态时并不适用。

3.2 VKNN 算法

本文在面向给定数据时，首先利用前文ISMOTE算法对数据本身进行优化，将优化后的数据传递给KNN。优化后的数据刚好规避了传统KNN 算法最大的几个问题，能够更加有效地对数据进行计算。

在传统KNN 算法中，k的取值一直是一个比较困扰的问题。如果k值过低可能会出现过拟合的问题，不能很好地泛化。如果k值过高可能使得模型过于泛化，出现欠拟合的问题[17]。针对此问题，本文不再使用KNN 算法中根据k近邻样本点种类作为分类依据的原则。通过利用粒子群算法寻优速度快的特点首先对训练集样本点进行中心点搜索，随后计算同簇样本点到中心点距离均值作为分隔阈值对样本点进行分隔，最后对分隔后的样本点进行种类“投票”处理并输出分类结果。在粒子群算法中，个体和群体间需要不断交互信息从而寻找最优解。在此过程中，粒子通过式(10)和式(11)不断更新自己的速度Vid和位置Xid。

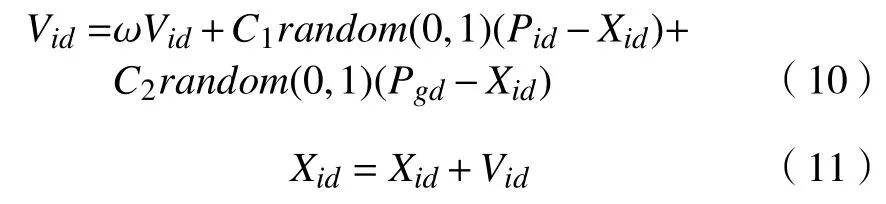
式中：ω为惯性因子；C1与C2为加速常数，一般取2；Pid为第i个变量的个体极值的第d维度；Pgd表示全局最优解的第d维度。

当满足最大迭代次数时迭代停止并输出最优解。

a.样本点集合为

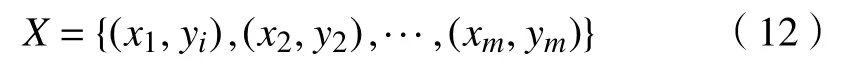
b.建立适应度函数为

搜寻到的样本点xn中心坐标为(xn,yn)。

c.根据欧氏距离式(6)对同簇样本点到该种类样本分布中心进行计算，计算出的距离合集D={d1,d2,···,dm}，根据式(12)计算同簇样本到中心点距离均值

d.若di＜，则纳入隔离样本集Dnew。

e.判断Dnew中多数类样本种类并作为最终输出结果。

相比传统KNN，该算法克服了因为k取值不同而会出现不同分类结果的问题，针对相同数据集VKNN 算法每次分类结果都相同。同时，通过引入粒子群算法可以最大程度提升VKNN 算法的计算效率，避免在寻找同簇样本距离均值过程中花费太多计算时间。在实际生产过程中，尽可能减少计算时间与尽可能提高算法计算效率无疑会给企业生产效率带来巨大提升。

4 基于ISMOTE-VKNN 的算法流程

基于ISMOTE-VKNN 算法流程如下：

a.收集设备状态的数据，将其数据进行预处理后按照2∶1 的比例分为训练集与测试集。

b.根据企业要求确定噪声标准α，计算每个少数类样本的噪声系数β并进行比较，从而选择合适的样本点。

c.设置距离阈值dmin并计算少数类样本距离d进行比较，选择合适的样本点。

d.通过计算k邻近值并判断样本状态选择不同的新增方式。

f.分隔样本点并生成Dnew。

g.进行投票，输出分类结果。

ISMOTE-VKNN 流程图如图3 所示。

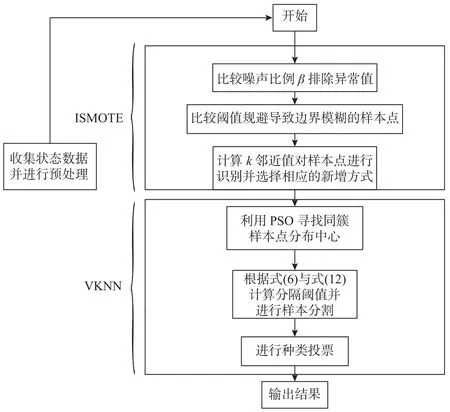
图3 ISMOTE-VKNN 算法分析流程图Fig.3 Flow chart of ISMOTE-VKNN algorithm analysis

5 ISMOTE_VKNN 仿真分析

5.1 数据来源

使用美国卡特彼勒公司液压泵与凌津滩水电站8 号机水导轴承状态数据进行实验，通过该数据以验证SMOTE_KNN 算法的有效性。液压泵与水导机器的故障一般是以轴承振动的方式表现出来，液压泵实验每隔10 min 进行一次约1 min 的设备振动数据收集，随后对收集的数据进行特征提取以达到能够被本文模型处理的要求。水导轴承实验通过记录不同负荷下的轴承横向与纵向振动数据以分析轴承的寿命情况。本文将液压泵前2/3 的数据用于训练，用剩下1/3 的数据进行测试以验证模型的有效性。同时针对水导轴承数据采用同样的方式进行模型验证，具体步骤和前者相同并省略。仿真环境为Anaconda 3.0。

5.2 数据分布

为了表现出ISMOTE_KNN 算法的优越性，本文将初始的多维数据进行拆分处理，即将原本的多维数据分为n个二维数据并挑选其中一组进行验证。使用CH1-1 与CH1-9 振动数据进行模拟。图4 为进行处理后的二维振动数据点位分布。

图4 振动数据点位分布Fig.4 Distribution of vibration data points

从图4 中可以看出，少数类样本中存在孤立于多数类样本中的异常值点。其中，黑色点为振动数据存在异常的点，橙色点为状况健康的点，黑色类为少数类样本，橙色类为多数类样本。该数据无法直接用传统KNN 算法进行处理，如果直接使用SMOTE 算法进行处理会出现上文描述的大量问题，因此，需要使用ISMOTE 对数据进行优化以达到KNN 算法使用的标准。

5.3 ISMOTE 算法

通过应用贝叶斯后验概率[18]计算得出k取4，通过对少数类样本计算噪声比例并设置阈值可以将其中的异常值点找出。这里噪声比例α取0.1。通过对所有少数类样本点计算噪声比例β，得到如表1 所示的结果。

表1 β 与阈值α 的比较结果Tab.1 Comparison results for β and threshold α

很明显存在一个异常值点，该点β值为0，将其剔除。

即使将异常值点剔除，剩余的少数类样本依然存在与多数类样本十分接近的点。因此，将dmin设置为0.5，忽略容易导致边界模糊的点。

利用ISMOTE_KNN 模型设置距离阈值m=0.5，k=4，同时通过计算可得模型中的少数类样本点均为半正常样本，随机性地对符合新增要求的样本点进行新增处理。将数据按照ISMOTE 算法进行处理可得到新增样本数据如图5 所示。

图5 ISMOTE 算法处理后的数据分布Fig.5 Data distribution after ISMOTE algorithm processing

在新增样本点过程中，为了保证ISMOTE 算法不会影响原始数据的特征，提取原始数据与新增数据的异常点拟合寿命曲线如图6 所示。

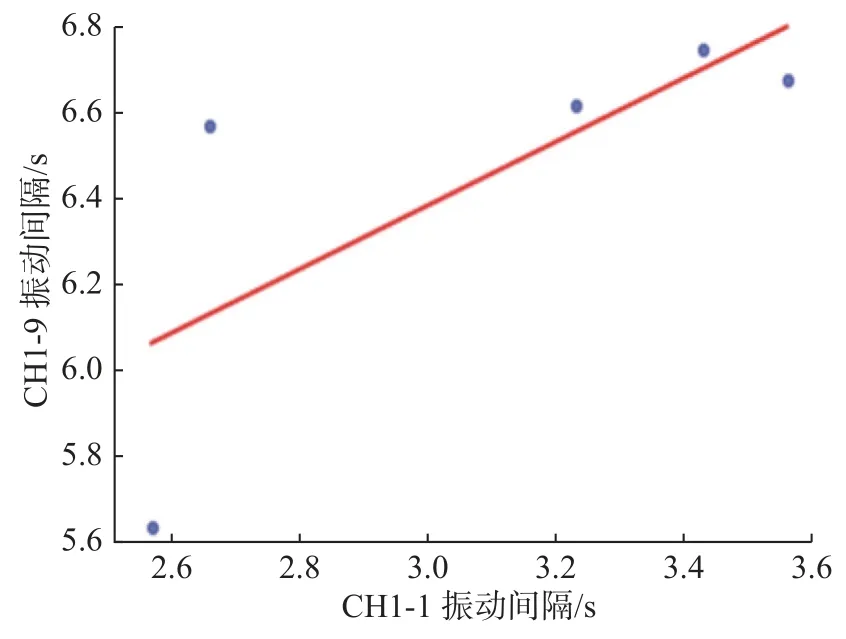
图6 原始异常数据点拟合曲线Fig.6 Fitting curve of original abnormal data points

如图7 所示，在进行ISMOTE 新增处理后的数据几乎不会影响原始数据点的寿命拟合曲线，因此，使用ISMOTE 算法优化数据是有效、可行的。

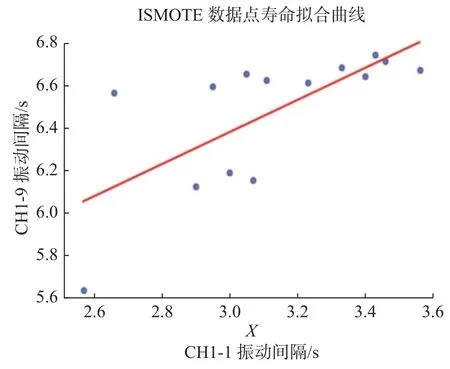
图7 ISMOTE 异常数据点拟合曲线Fig.7 Fitting curve of ISMOTE abnormal data points

5.4 VKNN 算法

在ISMOTE 的基础上引入VKNN 算法。其中，在PSO 算法中，经过实验确定 ωini=0.9，ωend=0.4，C1=C2=1.5，最大迭代次数为100。

最终PSO 输出的同簇样本中心分别为(3.12，6.45)与(2.29，6.16)。根据式(12)计算出=0.373，=0.411。由此对样本点进行分割处理，对处理后的数据种类进行分类并利用“投票”选择最终结果。

用12 组测试数据利用VKNN 算法对设备健康状况处理结果如表2 所示。

表2 ISMOTE_VKNN 设备数据预测结果Tab.2 Prediction results of equipment data based on ISMOTE_VKNN

如果不使用ISMOTE_VKNN 算法，直接进行KNN 算法计算结果如表3 所示。

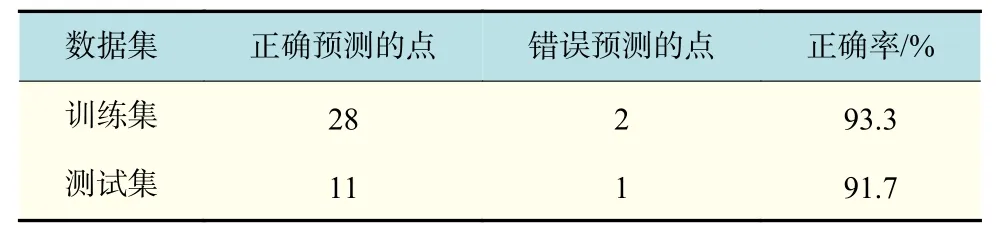
表3 KNN 设备数据预测结果Tab.3 Equipment data prediction results based on VKNN

通过比对可以表明，相比传统KNN 算法，ISMOTE_VKNN 算法拥有更高的准确性，并且2 种算法的耗时在面对小样本数据的时候都很短，在时间上也继承了KNN 算法的快速性。

同时为了保证ISMOTE_KNN 算法的优越性，而利用同样的测试集与训练集，在ISMOTE 优化数据的基础上利用非线性SVM[19-20]以及仅仅对原始数据用非线性SVM 进行分类效果如表4 所示。

表4 SVM 与ISMOTE_SVM 处理结果Tab.4 SVM and ISMOTE_ SVM processing results

由于测试集样本容量较小，所以，ISMOTE 算法的优越性主要体现在了容量相对较大的训练集上。

将以上结果进行整合如表5 所示。

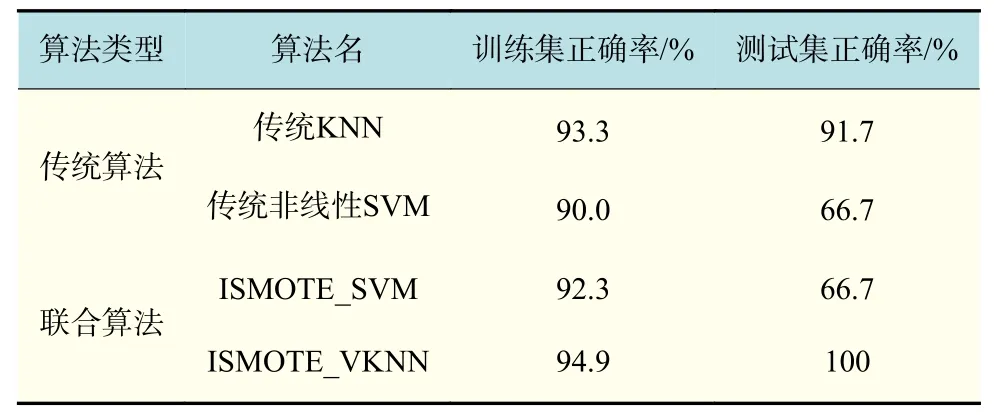
表5 液压泵各算法正确率展示表Tab.5 The correct rate of each algorithm of hydraulic pump

可以看出，在液压泵小样本情况下虽然训练集错误率已经明显降低，但是，由于测试集的错误率偏高，几乎接近直接使用KNN 算法进行计算的错误率，由此可以看出，ISMOTE_KNN 算法在小样本数据处理中的优越性。

利用同样的方式对水导轴承的振动数据进行分析和计算，得到的结果如表6 所示。

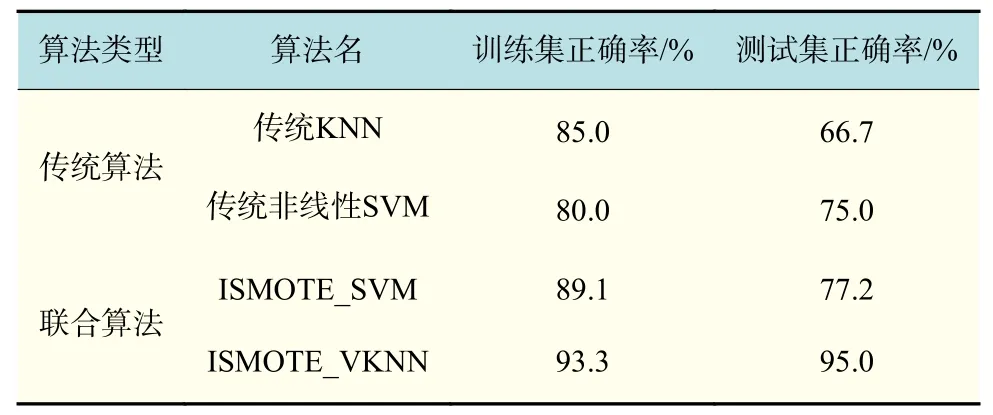
表6 水导轴承各算法正确率展示表Tab.6 Accuracy display table of hydraulic guide bearing

通过国内的水导轴承振动数据分析可知，ISMOTE_KNN 算法在实际应用中相比传统机器学习算法以及其他联合算法拥有更好的分类效果，即便是少数类样本容量不足也能够对其数据进行处理。相比大多数情况下使用的SVM，本文的算法能够更加准确地对液压泵状态进行分析从而淘汰那些状态异常的设备。

5.5 剩余寿命预测

在实际工业中，设备振动方均根值RMS能够体现设备健康状况，因此，本文通过对设备训练集与测试集数据点的RMS数值进行观察，观察结果可作为分析设备健康状况的依据。本文数据点的RMS数据计算结果如图8 所示。

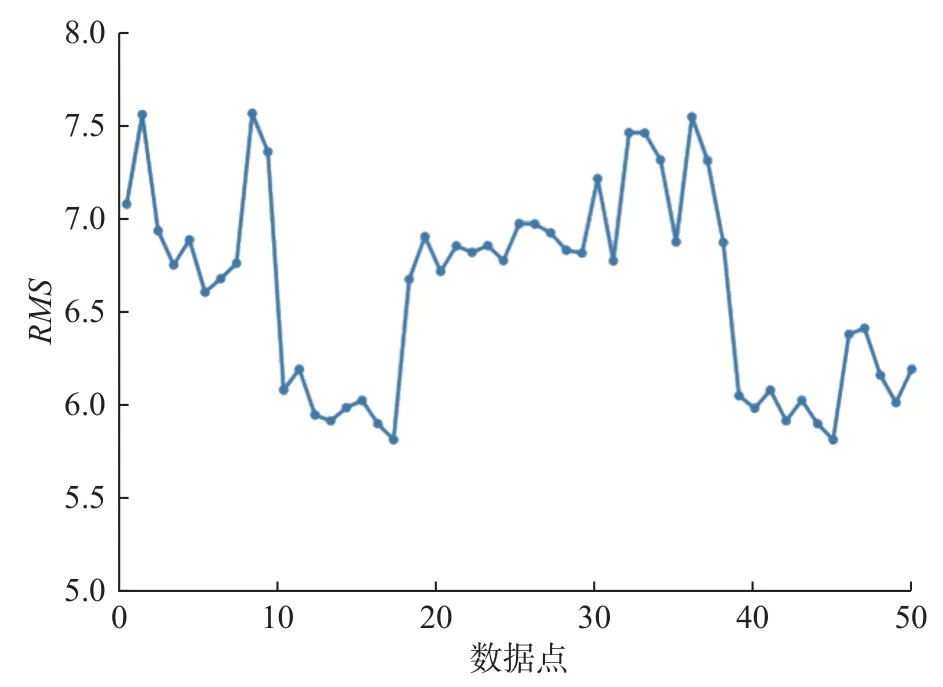
图8 设备数据点RMS 监视数据Fig.8 RMS monitoring data of equipment data points

根据设备的健康状况以及对数据点的分析，当RMS数据区趋于7 及以上的时候设备健康状况将会导致设备无法完成预计的生产目标。因此，本文着重对7 及以上RMS的数据点进行分析和预估并拟合数据线性趋势。其中，设备真实RMS数据值与预测RMS数据对比图如图9 所示。

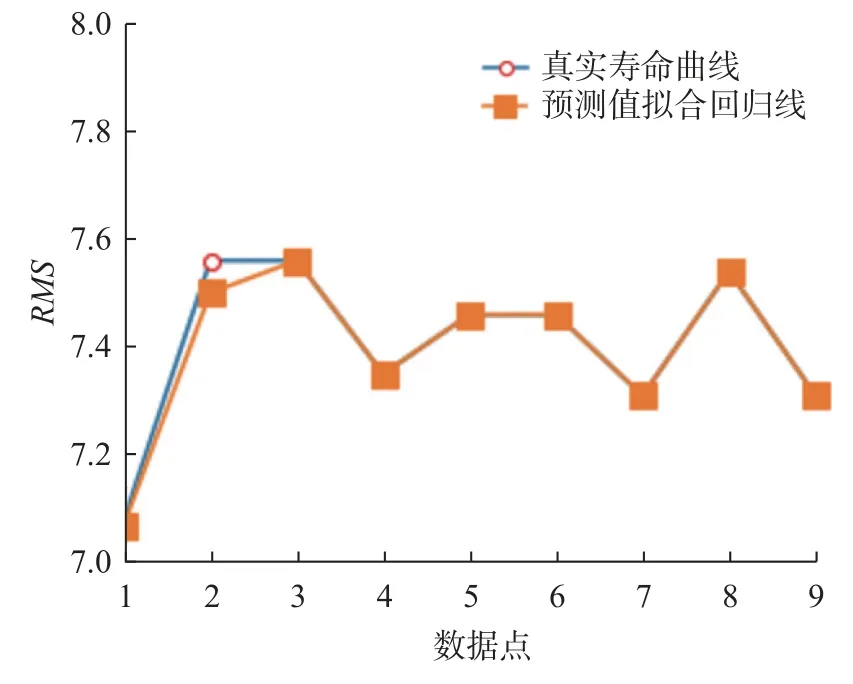
图9 RMS 实际值与测试值比较图Fig.9 Comparisons of RMS actual value and test value

同样地，对轴承的振动数据进行分析并拟合出机器剩余寿命RUL预测曲线如图10 所示。

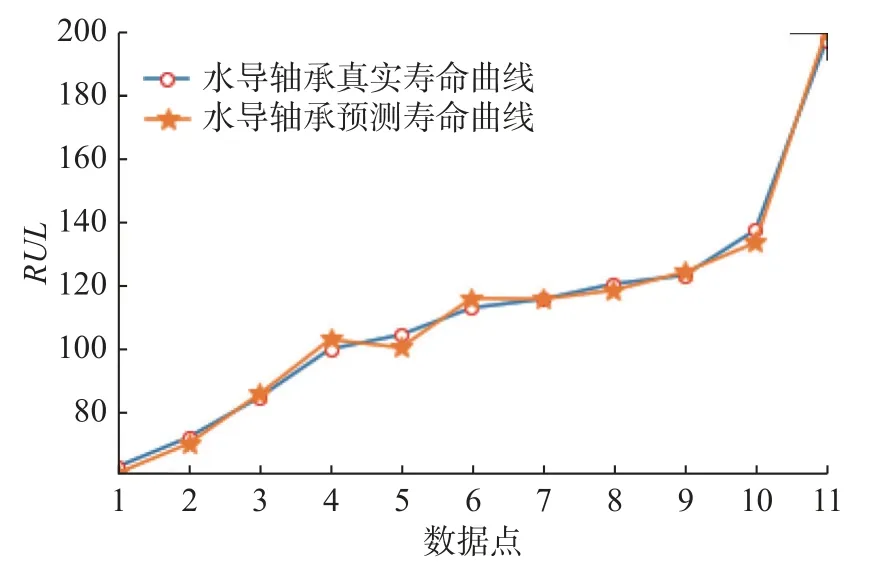
图10 水导轴承RUL 实际值与测试值比较图Fig.10 Comparison between actual RUL value and test value of hydraulic guide bearing

通过观察2 个设备真实RMS数据线性拟合结果与本文算法的预测拟合结果可知，两者具有高度的相似性，因而可以证明本文提出的算法在数据处理中不仅可以保证不会破坏数据的特征，同时也可以准确分析出设备健康状况以及预测设备未来寿命发展趋势，进而可以避免实际工业中因为设备健康问题而造成的经济损失。

6 结束语

通过引入SMOTE 算法弥补KNN 算法存在的局限性，同时针对传统SMOTE 算法的不足进行改进，通过设置噪声比例β消除存在于多数类样本附近的少数类样本噪声，再通过设置阈值dmin忽略那些新增后容易导致边界模糊的少数类样本点，选择性地对部分优秀的样本点进行新增处理，提高了新增样本点的质量，规避了传统SMOTE 算法存在的局限性。最后通过PSO 寻找同簇样本中心，建立分隔阈值对样本点进行裁剪并投票，规避KNN 算法面对交错数据无法准确分类的问题。仿真部分比较了各种算法下液压泵与水导轴承的健康状况分析准确度。算例表明，本文提出的联合算法相比传统机器学习算法具有更高的准确性。在面对大规模数据时，当数据本身呈现出紧密离散型分布特点并且样本分布毫无规律时，本文提出的改进算法由于法则限制会出现较大偏差，在此情况下可以适当抛弃ISMOTE 并需要对后续的机器学习改进算法进行进一步提升。在保持计算精度要求的前提下可以对VKNN 算法进行集成处理输出强学习器Adaboost。为了保证该集成算法的计算速率，后续可以从样本权值与弱学习器权值方面对Adaboost 进行进一步优化以满足计算速率要求。同时为了适应实际工业中多维数据的情况，本文提出的算法在未来改进后应尽可能实现同时对多个因变量进行分析的功能，规避分类讨论的局限性，由此满足实际工业中的各种需求。