基于RBF 神经网络滑模自抗扰的四旋翼飞行器控制

杨立本，汤裕民，李泰国，王 栋

(1.兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070；2.中国航天科技集团第五研究院 510 所，甘肃 兰州 710072)

四旋翼飞行器因其结构简单、机动性能好、易操作，在垂直起降、悬停和低速等方面表现优异，在航拍、物流投递、搜救等方面得到了广泛的应用[1-3]，成为近年来的研究热点.由于四旋翼飞行器非线性、强耦合、欠驱动、易受干扰等特点，所以控制器设计应有较强的抗干扰能力和鲁棒性，给控制器设计带来了挑战.

针对四旋翼飞行器的欠驱动、强耦合特性，目前已有Proportional Integral Derivative（PID）控制、H∞控制、滑模控制、反步控制、自适应控制、鲁棒控制等，但四旋翼飞行器在飞行过程中往往受到内部不确定性和外界未知扰动的影响，基于这些方法的飞行控制系统存在一定的局限性.文献[4-5]提出PID 控制，该方法比较成熟且易于实现，不依赖于对象模型，但是传统PID 控制动态性能差，调节时间长且超调大，参数无法适应系统外部的扰动因素.文献[6-7]设计了滑模控制器，通过仿真实验验证了所设计的控制器优于PID 控制，但没有考虑到系统的建模误差以及外部扰动的影响，且滑模控制抖振现象未进行改进.文献[8-10]提出的自适应控制，自适应控制算法可以补偿被控对象参数带来的变化，实时修改控制参数，但设计复杂，不易于实现.文献[11-12]设计了反步滑模控制器，通过实验证明所设计的控制器在响应速度和控制精度较好，但是反步法的引入加大控制器的运算量.

上述控制算法依赖于控制对象模型的精确性，易受模型精度的影响，对外界抗干扰能力较差，为了有效提高四旋翼飞行器对自身参数不确定和外部环境干扰性等因素的适应能力.本文提出的内外环嵌套控制系统中，外环为位置环，内环为姿态环.其中，外环的子系统为径向基函数（Radial Basis Function，RBF）神经网络滑模控制系统，其运用RBF 神经网络的自适应能力对系统模型中的未知常量和滑模控制器输出误差进行逼近，消除系统建模误差以及改善滑模控制初始时的抖振问题，并通过李雅普诺夫稳定法证明了所设计控制器的稳定性.本文提出基于自抗扰控制为内环的子系统，不依赖于系统精准模型，运用扩张状态观测器对外部扰动进行实时估计并对扰动带来的误差进行补偿，实现四旋翼飞行器的位置控制、姿态控制和飞行轨迹跟踪控制，通过仿真实验验证控制系统的有效性和鲁棒性.

1 四旋翼飞行器建模

四旋翼飞行器由十字支架和4 个带螺旋桨的电机组成，通过改变4 个电机的转速调节螺旋桨转速，4 个电机通过螺旋桨产生向上的推力Fi，各电机转速 ωi不同产生不同的力矩，这些力矩叠加为合力矩，旋转的加速度由4 个电机产生的合力矩决定，影响飞行器的飞行姿态.如图1 所示，1 号、3 号电机顺时针旋转，2 号、4 号电机逆时针旋转，抵消了旋翼之间的反扭力矩.

如图1 所示建立四旋翼飞行器机体坐标系xbybzb和地面坐标系xeyeze，机体坐标系原点Ob选在飞行器的重心上，地面坐标系原点Oe与地面固连.

图1 四旋翼飞行器结构图Fig.1 Structure diagram of Quadrotor aircraft

为了简化动力学模型，对四旋翼飞行器做出如下假设：①飞行器机身是刚体，结构完全对称；②飞行器机身坐标系原点与质量重合；③每个旋翼产生的升力和受到的反扭距都与旋翼的转速平方成正比.

忽略空气阻力，四旋翼飞行器系统的数学模型为：

式中，x、y、z是飞行器的位置变量，θ 为俯仰角，ϕ为滚转角，ψ 为偏航，Ix、Iy、Iz分别为绕机体坐标系的转动惯量，m为飞行器的质量，g为重力加速度，l为旋转子与飞行器质心之间的距离，d1、d2、d3、d4、d5、d6分别为飞行器6 个通道的扰动，输入控制量U1、U2、U3、U4与 电机转速 ωi之间的关系为：

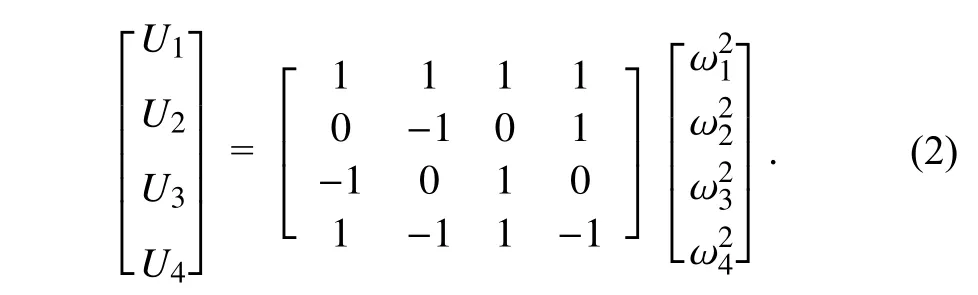
将飞行器分为位置外环和姿态内环，取虚拟控制量：

由（4）式和期望偏航角 ψd可以反解算出U1、期望的俯仰角 θd和滚转角 ϕd的控制输入指令为：

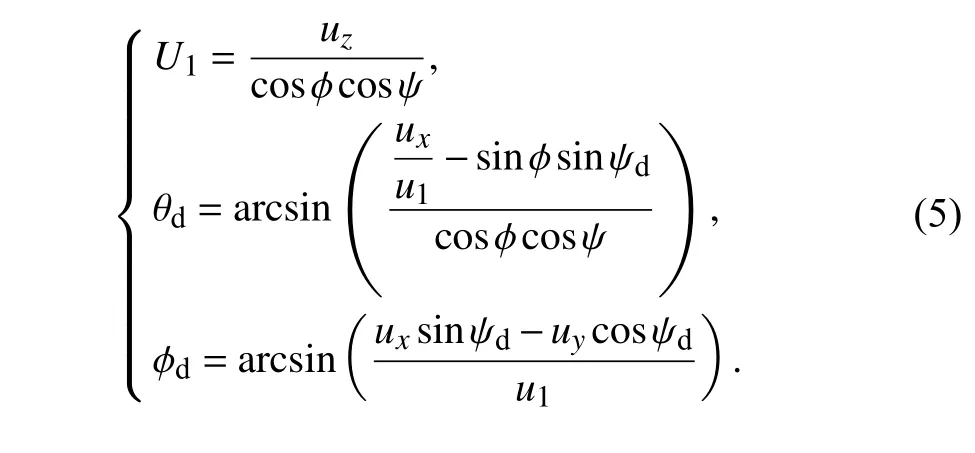
2 四旋翼飞行器控制器设计

四旋翼飞行器是具有4 个控制输入和6 个控制输出的欠驱动系统，控制系统采用串级控制方式，以位置子系统为外环，以姿态子系统为内环，将其分为4 个通道：高度z通道、x-θ 通道、y-ϕ通道和偏航 ψ通道.由于四旋翼飞行器参数不确定性和易受外界干扰，为了实现飞行器能快速平稳地跟踪预定的飞行轨迹，本文提出了以RBF 神经网络滑模控制为外环、自抗扰控制为内环的内外环嵌套的控制策略控制飞行器.控制系统结构框图如图2 所示，xd、yd、zd为期望位置信号，ux、uy为虚拟控制量，u1为 高度控制信号，u2、u3、u4为姿态角控制信号.

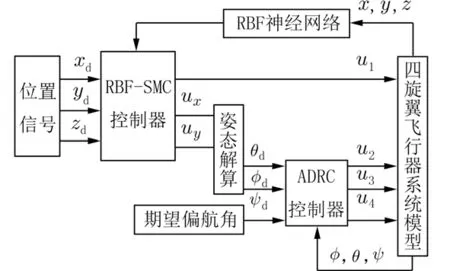
图2 控制系统结构框图Fig.2 Structure diagram of control system

2.1 位置控制器设计滑模控制能使四旋翼飞行器稳定飞行，但在系统初始状态到达滑模面后发生抖振现象，RBF 神经网络的自适应能力对滑模控制器输出误差进行逼近，对滑模切换增益实时调节，减小了滑模控制产生的抖振问题.

2.1.1 滑模控制器设计 滑模控制器能让系统状态随时间变化，使系统稳定在滑模面附近，通过切换函数让系统收敛于滑模面，使得系统按照预定状态轨迹运动,设计所需的滑模面和控制律，能快速响应输入的变换，具有很好的鲁棒性.

四旋翼飞行器实际位置运动轨迹与期望位置运动轨迹产生的误差定义为：

式中，xd、yd、zd为期望位置轨迹，x、y、z为实际轨迹.

根据滑模面定义，设计滑模函数：

因此，当s1⇒0 时，可以推导出，即误差指数速度趋近于0.对s进行求导，可以得出：

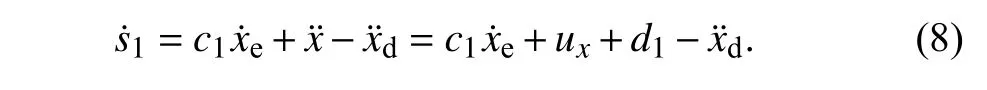
针对动力学模型以及存在扰动，设计滑模趋近律如下式所示：

因此可以设计滑模控制律：

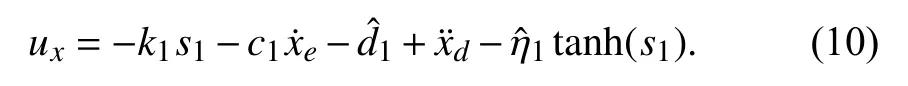
2.1.2 RBF 神经网络滑模控制器设计 RBF 神经网络是单层神经元结构的神经网络，是一种高效前馈神经网络，能在任意精度下适应非线性函数，通过与滑模控制相结合，有效地减小了滑模控制带来的抖振问题.

以x方向为例：设定d1为四旋翼飞行器扰动项，需要对不确定对扰动和不确定项进行逼近.采用RBF 神经网络对d1进行自适应逼近补偿，本文RBF 神经网络采用高斯函数形式，网络算法为：

式中，h(x)为隐含层输出，x为输入，cj为高斯函数中心位置，bj为基宽参数，W为理想权值，ε为神经网络逼近误差且 ε ≤η1.

令：ε ≤η1，其中 η1为未知逼近误差上界，使用自适应控制律进行估计.

2.2 姿态控制器设计四旋翼飞行器的内环为姿态环，x-θ通道、y-ϕ 通道和偏航 ψ通道之间存在耦合特性，自抗扰控制由韩京清教授提出，不依赖于精准对象模型，实时估计系统内部扰动和外部未知扰动并进行补偿，包括跟踪微分器（Tracking Differentiator,TD）、扩张状态观测器（Eetended State Observer,ESO）、非线性误差反馈控制率（Nonlinear States Error Feedback,NLSEF）3 个部分组成[13-15].每个通道用扩张状态观测器对总扰动进行实时估计，并对扰动带来的误差进行补偿，实现飞行器的解耦控制.控制器结构如图3 所示.其中，v0为输入信号，v1为跟踪信号，v2为微分信号，e1、e2为误差和误差的微分，b0为控制输入缩放系数，z1、z2、z3分别为系统3 个状态变量的观测值，u、y分别为系统的输入和输出.

图3 自抗扰控制结构图Fig.3 Structure diagram of active disturbance rejection control

2.2.1 跟踪微分器 跟踪微分器安排过渡过程，对输入信号的噪声起到很好的抑制作用，扩大比例系数和微分系数取值范围，通过快速最优控制综合函数 fhan，避免了数字计算中的高频振颤出现，可以获得优质的微分信号，不仅可以解决超调与快速性矛盾，还可以使误差反馈增益和误差微分反馈增益的选取范围扩大，表达式为：

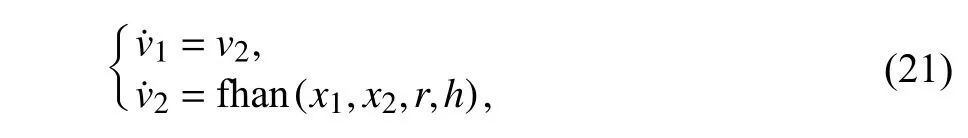
式中，fhan(x1,x2,r,h)为最速综合函数，r为跟踪微分器的快速因子，h为运算步长，r、h参数可调，决定输出信号跟踪速度，r越大过渡过程越短，h越大滤波效果越好.f han(x1,x2,r,h)表达式为：

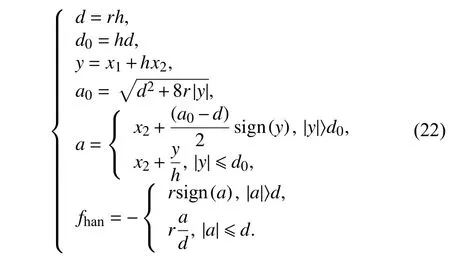
2.2.2 非线性状态误差反馈律 用于产生初始控制量，依据“小误差大增益，大误差小增益”的设计思路，将TD 产生的跟踪信号与ESO 估计出的系统状态进行组合，得到系统当前反馈控制量u0，最终的控制量u由虚拟控制量u0再加上总扰动估计的补偿值来确定，表达式为：

式中，k1和k2影 响系统响应速度，增大k1，系统响应速度越快，增大k2可 以抑制振荡和超调，fal(e,a,δ)为饱和非线性函数.

2.2.3 扩张状态观测器 扩张状态观测器的参数影响扰动估计和补偿，将系统其他回路的耦合影响和系统内部不确定性和外部扰动视为总扰动进行观测补偿，不依赖生成干扰的数学模型，使系统转化为的“积分串联型”系统，表达式为：

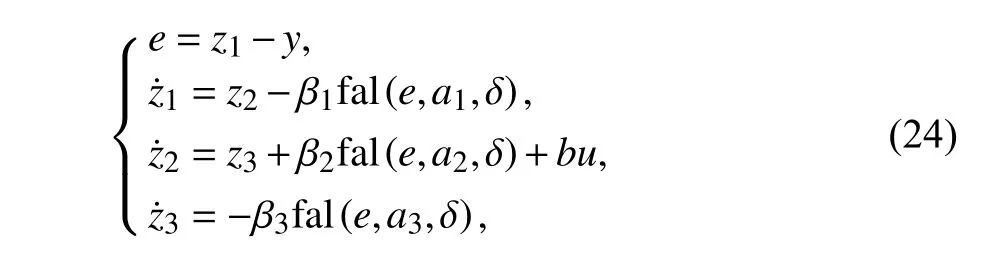
式中，δ、β1、β2、β3为一组待整定参数，u和y为系统输入输出信号，b0为控制输入缩放系数，饱和非线性函数 fal(e,a,δ)为：

3 仿真分析

3.1 仿真参数根据式(1)建立的四旋翼飞行器的数学模型和图2 所示的控制系统框图，为了验证本文提出的控制方法的有效性和控制系统的抗扰动、轨迹跟踪以及鲁棒性，在Matlab/Simulink 中搭建仿真模型进行仿真实验，四旋翼飞行器物理参数如表1 所示.内环ADRC 参数如表2 所示.

表1 四旋翼飞行器物理模型参数Tab.1 Parameters of the quadrotor aircraft physical model

表2 内环ADRC 控制器参数Tab.2 Parameters of the inner ring ADRC controller

3.2 仿真结果分析在不考虑外界干扰的条件下，给定期望位置和期望姿态角，根据所设计的控制器的期望位置和姿态角进行对比，验证所设计控制器的正确性.在考虑干扰信号的条件下，给定期望姿态角，进行姿态角跟踪实验.最后进行飞行轨迹跟踪实验.

图4 为位置轨迹跟踪曲线，xd、yd、zd为位置期望值，与滑模控制位置轨迹、RBF 神经网络滑模控制位置轨迹x、y、z进行对比，仿真初始条件是x=0.5 m、y=0 m、z=2 m，仿真时间30 s，由图4 可以看出，x方向RBF-SMC 在4.5 s 时刻能跟踪上期望轨迹，SMC 出现较大抖振，在8.6 s 时刻才能完全跟踪上期望轨迹，RBF-SMC 比SMC 快4.1 s，y方向RBF-SMC 和SMC 在0.5 s 时刻同时追踪上期望轨迹，z方向SMC 在初始时有明显抖振问题.虽然SMC 也能够较快跟踪上期望信号，但是初始时刻跟踪误差较大.本文所设计的RBF 神经网络滑模控制器能够较好地跟踪期望位置轨迹，有效地改善了滑模控制带来的抖振问题.

图4 位置轨迹跟踪曲线Fig.4 Position trajectory tracking curve

图5 为滑模面收敛和抖振情况，S1、S2 分别为x,y方向滑模面情况，收敛在一个区域范围内，在趋近于0 时，会产生抖振现象，可见滑模面收敛有改善.

图5 滑模面收敛和抖振情况Fig.5 Convergence and chattering of sliding mode surface

神经网络具体作用是逼近外界干扰，并把预估外界干扰给补偿进控制律，在x、y通道内设置的干扰量与神经网络的输出量的比较关系如图6 和图7 所示，两图所示神经网络输出量能很好地补偿对应方向的干扰量.

图6 x 方向干扰与神经网络估计Fig.6 Estimation of x-direction disturbance and neural network

图7 y 方向干扰与神经网络估计Fig.7 Estimation of y-direction disturbance and neural network

图8 为姿态轨迹跟踪曲线，ϕd、θd、ψd分别为滚转、俯仰、偏航姿态的期望值，与实际的滚转角ϕ、俯仰角θ、偏航角 ψ姿态轨迹跟踪进行对比，仿真时间30 s，不考虑干扰时，姿态控制仿真初始条件ϕ=−1.5 rad，θ=1.5 rad，ψ=1 rad，由图可以看出，姿态控制器能很好地跟踪姿态期望值.

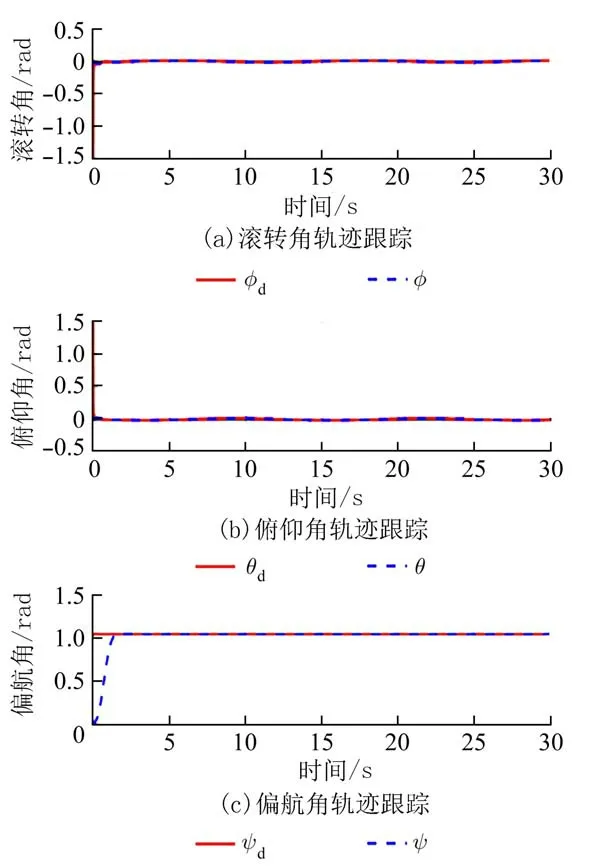
图8 姿态轨迹跟踪曲线Fig.8 Attitude trajectory tracking curve

图9 为给定干扰信号下姿态环的轨迹跟踪，ϕd、θd、ψd为 姿态期望值，ϕ、θ、ψ为干扰信号下的姿态实际值，在俯仰、滚转、偏航3 个通道分别加入白噪声模拟扰动信号：

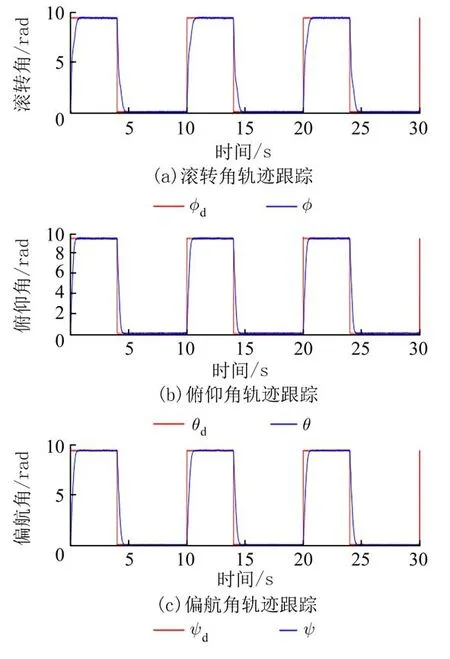
图9 干扰下姿态角轨迹跟踪Fig.9 Attitude angle trajectory tracking under disturbance

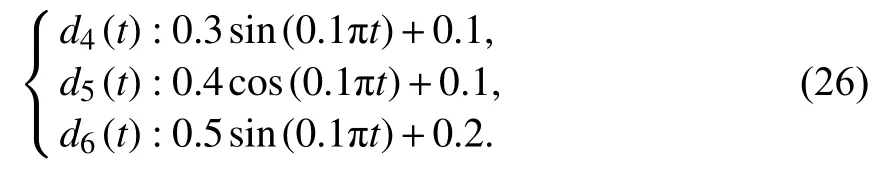
进行扰动信号下姿态角轨迹跟踪实验，在相同的姿态角初始条件下，分别给出了四旋翼飞行器在给定扰动信号d4(t),d5(t),d6(t)影响下俯仰、滚转、偏航3 个通道姿态角的跟踪轨迹，设定值幅值为9.8°的方波，仿真时间为30 s，在扰动信号下，能够较好地使四旋翼飞行器的姿态角跟踪给定值，说明所设计的控制器能有效地抑制干扰，保证闭环系统的稳定性，对具有强耦合性的四旋翼飞行器姿态系统进行有效控制.

图10 为升力U1、滚转角 ϕ、俯仰角θ、偏航角ψ的输出控制率，可以看到升力U1最终达到稳定，而滚转角 ϕ、俯仰角θ、偏航角 ψ的输出控制率在1 s收敛至稳态值，姿态角能很好跟踪给定值.

图10 姿态角输出控制率Fig.10 Attitude angle output control rate

图11 为四旋翼飞行器三维飞行轨迹跟踪，将期望飞行轨迹、RBF 神经网络滑模控制与自抗扰控制（RBF-SMC+ADRC）相结合的飞行轨迹和滑模控制（SMC）飞行轨迹进行比较，假设四旋翼飞行器初始状态保持静止，设置初始位置为(000)T，初始姿态为(000)T.偏航角设定值为60◦，期望轨迹为：

仿真时间为30 s，初始高度为0 m，总高为6 m，从高度2 m 开始追踪.由图11 可知，滑模控制在初始时有明显“抖振”，所设计的RBF 神经网络滑模控制与自抗扰控制相结合的控制策略能够快速地跟上期望的轨迹.在仿真开始时，设计的控制器轨迹跟踪比滑模控制器的轨迹跟踪时间要快10%，超调量明显更小，有效地减小了滑模控制带来的抖振问题，飞行轨迹跟踪实验结果稳定，在全程保持良好的跟踪飞行状态，证明了本文所设计的控制器有效性.

图11 四旋翼飞行器飞行轨迹跟踪Fig.11 Tracking of quadrotor aircraft flight trajectory

4 结束语

本文针对四旋翼飞行器非线性、强耦合、易受外界干扰等特点，提出了RBF 神经网络滑模控制与自抗扰控制相结合的控制策略.采用Lyapunov方法证明闭环系统稳定性，仿真实验表明，所设计的控制器不仅能有效抑制外部扰动，减小了滑模控制产生的抖振问题，能实现四旋翼飞行器姿态稳定跟踪和期望飞行轨迹准确跟踪.今后研究中，将不断改进优化控制方法，将其应用到实际四旋翼飞行器平台，以实现更好的控制效果.