基于神威超算平台的三维方柱绕流大规模并行数值计算与分析
2022-09-21张亚英吴乘胜王建春顾寒锋
张亚英,吴乘胜,王建春,顾寒锋
(1.中国船舶科学研究中心,江苏无锡 214082;2.国家超级计算无锡中心,江苏无锡 214072)
0 引 言
由于“主频墙”、“通信墙”和“功耗墙”等的限制,近年来超级计算机架构正在发生由同构向异构发展的变革。以2020年11月发布的超级计算机TOP500[1]榜单为例,其中约30%采用了加速卡或协处理器,且近十年来登顶的超级计算机均采用异构处理器或异构节点,这种趋势表明异构已经成为超级计算机的发展趋势,并在性能上有显著的优势。
异构与同构的差异在于:同构架构中所有的计算核心都由CPU构成,所有计算核心的逻辑处理能力和数据计算能力都很强,不受计算任务复杂度的影响;缺点是成本高、功耗大。异构与同构相比,计算核心的种类不同,一般包含CPU和协处理器,或者将两种不同功能的计算核心集成在单个芯片上形成异构众核处理器。异构系统通过CPU 调度加速硬件或加速核可以实现深层次的并行,使计算任务划分更加细化。典型的异构模式包括CPU+GPU、CPU+MIC,以及我国第一台全部采用自主技术构建的世界第一的超级计算机——“神威·太湖之光”所采用的SW26010处理器。
异构体系使超级计算机的计算能力大幅度提升,但同时对CFD 高性能计算也是挑战。要实现对计算资源的充分利用,需要从数值算法、数据结构、计算流程等各个层面进行重构和优化。在面向神威超算平台的CFD 并行计算方面,国内不少研究人员开展了研究工作。Ren等[2]将OpenFOAM 移植到“神威·太湖之光”上并进行了优化,优化后主从核协同使用,相较于纯主核应用加速了3.55 倍,单个SW26010 处理器较Intel x86 处理器加速了1.18 倍;对于CFD 的核心计算过程,倪鸿等[3]基于SW26010处理器架构对非结构网格下稀疏下三角方程求解进行了研究,提出了一种基于流水线串行-局部并行思想的通用众核优化方法,实现了单核组3 倍以上的加速效果;刘侃等[4]基于SW26010 处理器设计了针对三对角矩阵求解的并行算法swDCR,通过寄存器通信设计及双缓冲等,相较于主核加速约2.07倍;在CFD 适应性方面,李芳等[5]对CFD 中的隐式算法、多重网格等问题的众核并行难点进行了分析,给出了相应的并行方案,并对OpenCFD、SWLBM 以及AHL3D 等流体力学软件的众核适应性进行了讨论。
总体上看,国内CFD领域尤其是船舶水动力学CFD领域,目前远未实现对国产异构众核超算能力的有效利用。究其原因,除了CFD应用研究长期依赖国外商用软件之外,还包括以下客观因素:
(1)CFD 计算通常具有全局相关性的特点,并行规模的增大带来了并行复杂度与通讯开销的增加,导致并行效率下降;同时水动力学CFD常用的SIMPLE算法的流程相对复杂,增加了细粒度并行优化的难度,众核加速挑战很大;
(2)CFD 软件一般具有数据结构复杂、计算流程复杂和代码量庞大等特点,从程序的移植到优化,都需要大量的重构工作,难度和工作量巨大。
相较于上述对大型程序和局部迭代的移植和测试,本文更具针对性地对求解不可压流动问题的SIMPLE 算法,进行面向国产异构超算平台的并行计算研究。论文基于神威异构超算平台,采用自主开发代码,开展三维非定常不可压流动的大规模并行数值模拟研究。数值计算采用MPI+Athread多级并行方式,并在Athread众核并行中,针对申威众核处理器的特点对SIMPLE算法求解流程进行优化以提升加速效果。首先以三维方柱准定常绕流问题为例开展并行计算测试,包括MPI 并行和MPI+Athread 多级并行,证实多级并行的有效性;随后,针对三维方柱非定常绕流问题进行直接数值模拟,开展网格数量从384 万到2.46 亿的大规模并行计算并对计算结果进行分析,展现神威异构超算平台在非定常不可压缩流动CFD大规模并行计算方面的应用能力。
1 数值模拟并行计算方案
1.1 数值模拟方法简述
本文的主要目的是研究神威异构超算系统对三维不可压粘性流动CFD 核心求解过程的适应性,其积分形式控制方程组如下:
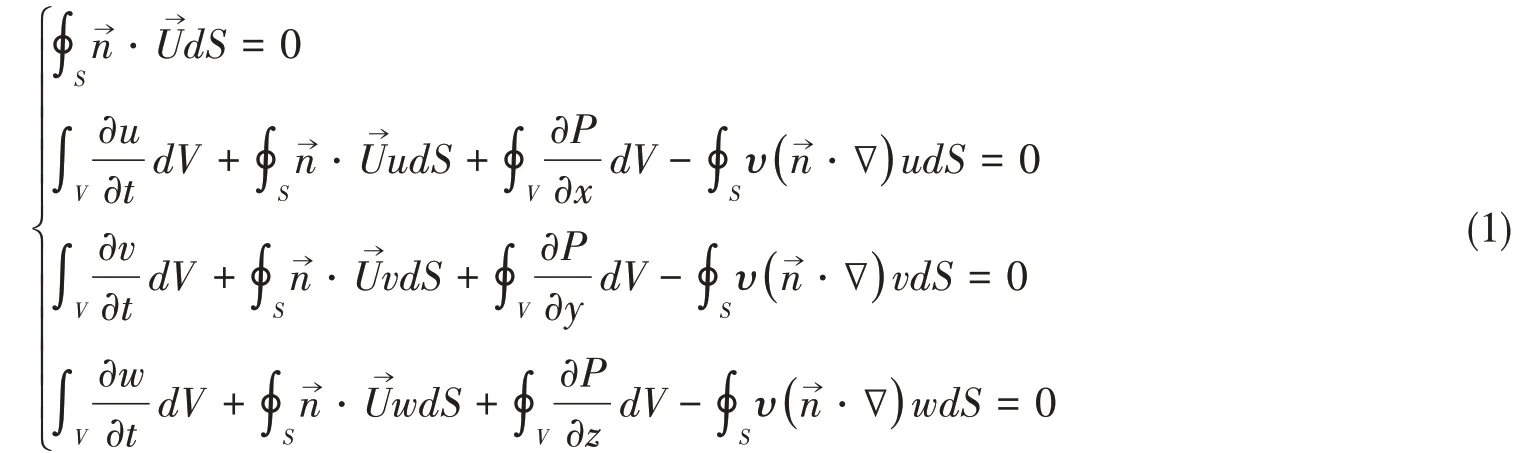
式中,V为控制体体积,S为控制体表面积,U→为速度矢量,其分量形式表示为(u,v,w),υ为流体运动粘性系数,U∞为无穷远处自由流速度。
采用基于交错网格的有限体积法离散控制方程,具体可参阅文献[6];控制方程组的求解采用SIMPLE算法[6]。
1.2 申威众核处理器简介
“神威·太湖之光”超级计算机,采用的是国产申威架构SW26010处理器。处理器本身就包括控制核心和计算核心阵列,相当于把CPU和加速处理器集成到一个芯片上,其内部架构如图1所示。
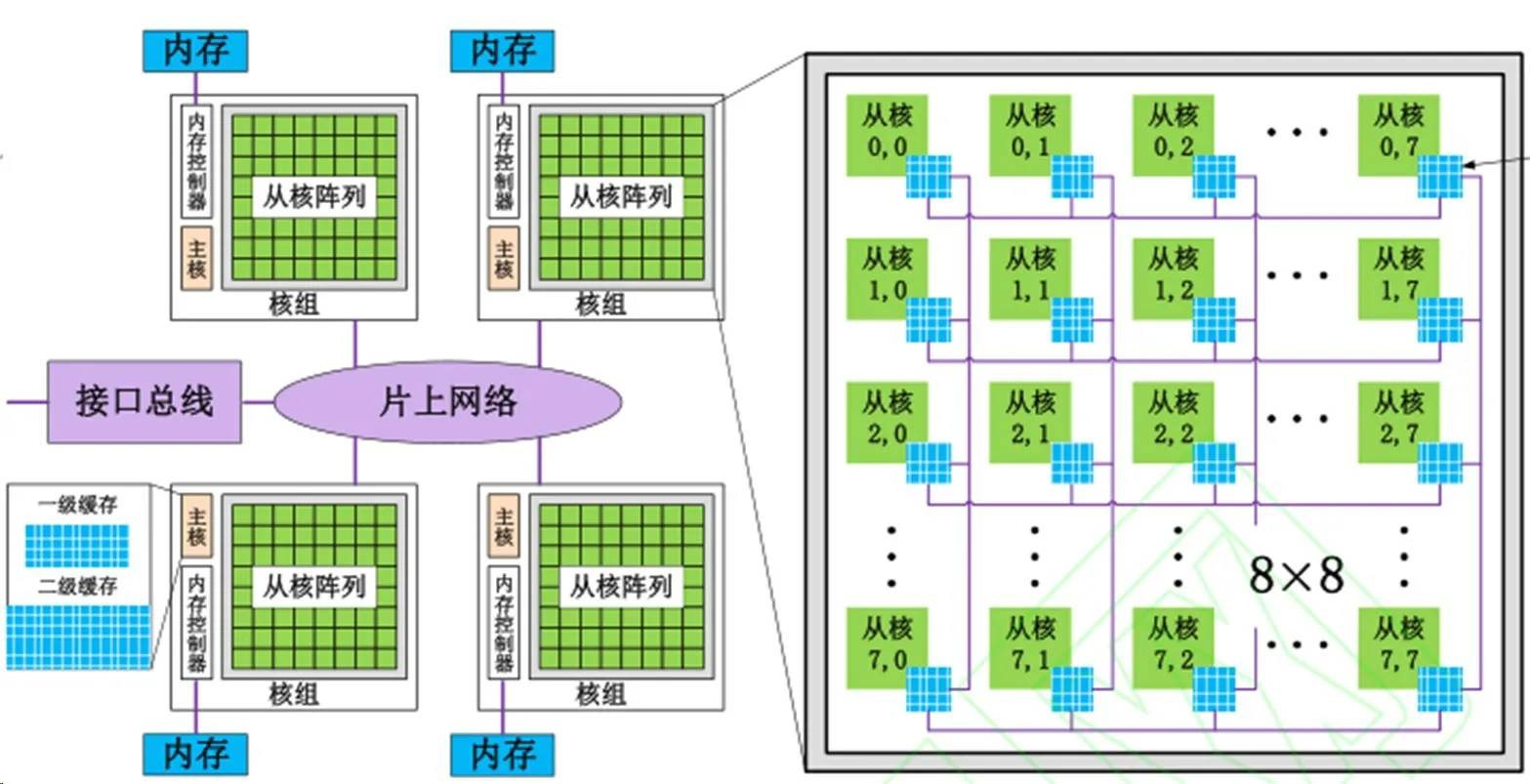
图1 SW26010处理器架构示意图Fig.1 Diagram of SW26010 architecture
SW26010 处理器包含四个核组(CG),各核组之间采用片上网络(NOC)互联,每个核组内包含一个主控制核心(主核,MPE)、1 个从核(CPE)集群(由64 个从核组成)、1 个协议处理单元(PPU)和1 个内存控制器(MC)。核组内采用共享存储架构,内存与主/从核之间可通过MC传输数据。
SW26010处理器的计算能力主要体现在从核上,但从核上的存储空间和带宽较小,使得数据传输往往成为程序运行的瓶颈,这也是并行方案设计中的重点。
1.3 并行计算方案
并行方案采用MPI+Athread的多级并行方式,其中:主核(核组)采用基于区域分解的MPI并行;从核并行则采用神威专用加速线程库Athread,方式为循环分解;SIMPLE 算法的迭代过程采用SOR 算法,并使用红黑排序进行分块,避免数据相关。
由于迭代过程具有全局特性,要保证计算结果的准确性需要实时更新影像区;而实时更新通信代价巨大,通常可以在保证结果精度的前提下适当减少通信次数。在本文中,由于内迭代次数较少,因而采用实时更新的方法保证结果的准确性。由此,在并行方案设计上,主要面临两方面的问题:SIMPLE算法迭代过程中的通信;从核有限内存空间的高效利用。
由于SW26010 处理器每个从核有64 kB的高速存储由程序员自己控制,从核访问这一局部存储空间(LDM)的速度非常快,而从核访问主存则会有很高的延迟(见表1)。所以在从核并行中,通常将主存中的数据以直接内存访问(DMA)的形式将数据传输到LDM空间(如图2所示)。

表1 SW26010处理器从核访存性能Tab.1 CPE performance of SW26010 processor
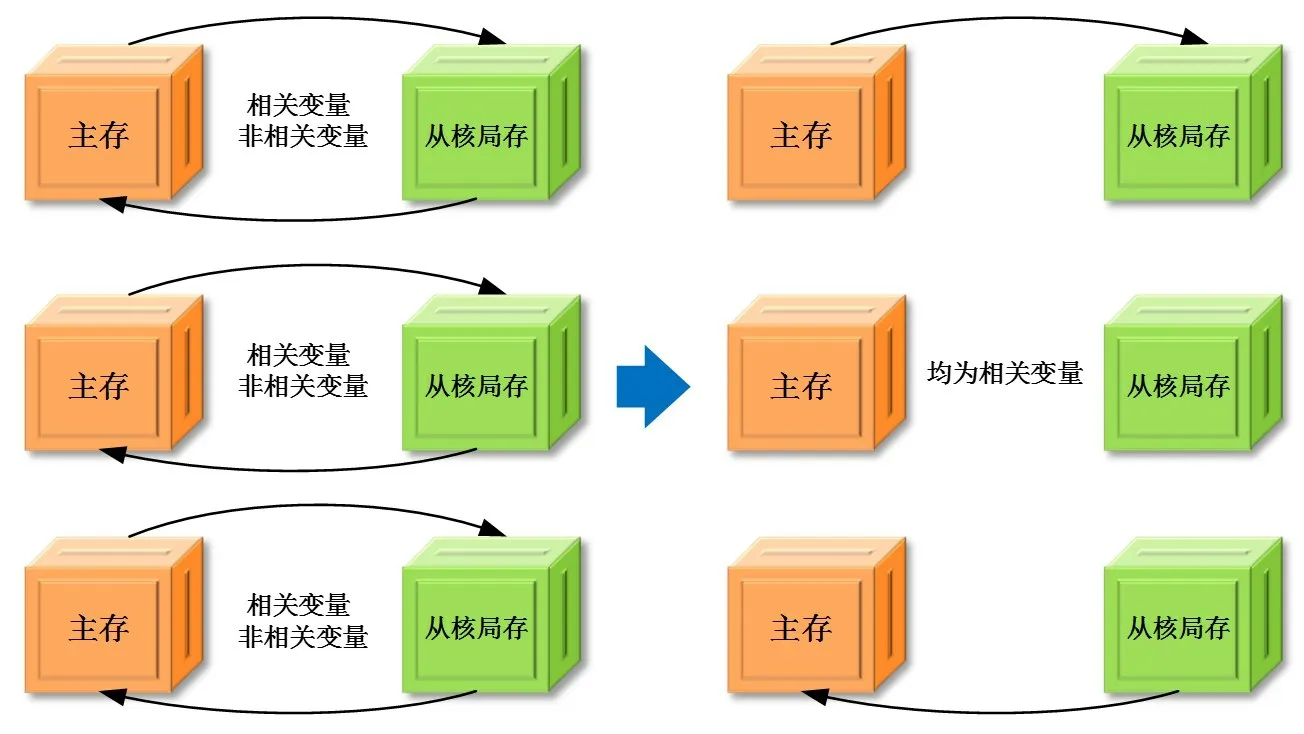
图2 循环融合前后变量有效性及通信变化Fig.2 Change of variable validity and communication before and after loop consolidation
CFD程序中,通常都会使用结构体。由于结构体中一般不可避免地存在“非相关变量”,从而降低从核存储空间的使用效率。如图2 左图所示,一个循环的众核并行,其LDM 空间由相关变量(relevant variables)和非相关变量(irrelevant variables)构成,结构体内“非相关变量”的传输既增加通信负担又占用从核存储空间;此外,过多的小循环也会增加通信频次。这些都会导致众核并行效率的降低。
为提高LDM 空间的使用和众核并行效率,本文采用循环融合的方式,对SIMPLE 算法的求解流程进行了优化,以增加结构体中变量的“有效性”,提高变量的复用度,避免同一变量的重复传输,如图2 右图所示。通过对二维方腔顶盖驱动流的众核并行测试,结果显示优化后的SIMPLE 算法求解流程,众核并行加速比提高了约25%(如图3所示)。
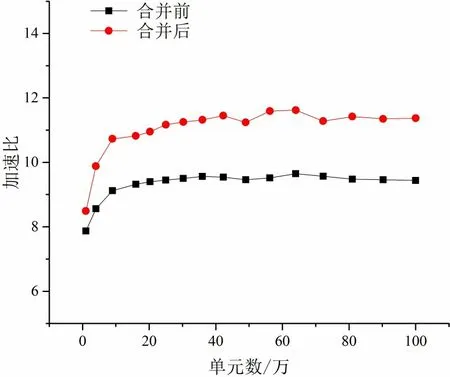
图3 SIMPLE算法计算流程优化前后众核并行加速比Fig.3 Many-core parallel speedup for SIMPLE algorithm before and after loop consolidation
2 并行计算测试
2.1 算例与计算结果
三维不可压流动问题的并行计算,以三维长方型截面柱体绕流为算例模型开展应用测试(如图4所示),表2 中为相关计算及模型参数,其中,h,l,m为柱体尺寸,并取d为特征长度。A,B,C表示计算域尺寸,D表示速度入口到柱体前壁面的距离,U为来流速度。设置Re=10,此时为准定常流动状态,便于对计算结果的准确性进行验证。

表2 三维方柱体绕流多级并行计算测试算例Tab.2 Test case of flow past 3D square cylinder for multilevel parallel computation

图4 三维方柱体绕流算例示意图Fig.4 Test case of flow past 3D square cylinder
图5 为流动状态达到稳定后的流线分布以及x方向速度云图,在中纵截面(y=1.5d)上柱体后方的涡心距离柱体后壁面约0.3d,高度约为0.25d,涡长度约为0.65d,与文献[7]结果一致。

图5 Re=10时三维矩形柱体绕流流线计算结果Fig.5 Computational result of streamline of flow past 3D square cylinder with Re=10
2.2 并行加速效果分析
分别对MPI 和MPI+Athread 的并行加速效果进行测试分析。MPI 并行测试主要分析其并行效率,考察其扩展性。不同网格数量算例下的MPI 并行加速比和并行效率分别见图6 和表3。并行加速比和并行效率计算分析中,由于单核内存无法处理大网格量算例,因而以2进程(2核)作为对比基准。

表3 不同网格数量算例MPI并行效率Tab.3 MPI parallel efficiency for cases with different grid numbers
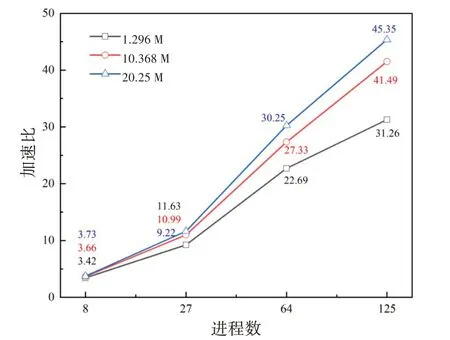
图6 不同网格数量算例MPI并行加速比Fig.6 MPI parallel speedup for cases with different grid numbers
从图表中可以看出:MPI并行加速比和并行效率都随着算例网格数量的增加而提高;相同网格规模下,MPI并行效率随着进程数(核数)增加而降低;对2025 万网格算例,125 进程并行计算加速约45倍(相对于2进程),并行效率约为72.5%。
为了保证计算精度,在SIMPLE 算法迭代过程中,采用了实时通信的方式,一定程度上降低了MPI的并行效果。在实际的CFD 计算中,可以综合考虑计算精度以及通信开销,适当减少通信频次,能够提高MPI并行效率。
在MPI 并行计算测试的基础上,开展了MPI+Athread 多级并行计算测试。不同网格数量算例下的多级并行加速比和众核并行加速比分别见图7和表4。

表4 不同网格数量算例众核并行加速比Tab.4 Many-core parallel speedup for cases with different grid numbers
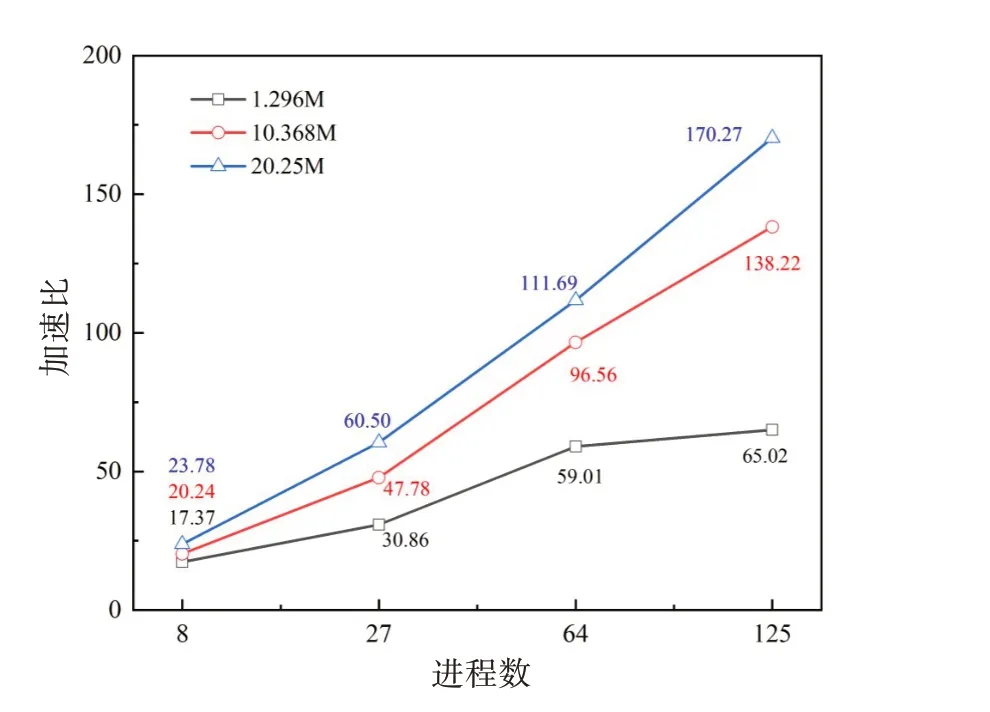
图7 不同网格数量算例MPI+Athread多级并行加速比Fig.7 MPI+Athread parallelspeedup for cases with different grid numbers
从图表中可以看出:MPI+Athread 多级并行和众核并行加速比都随着算例网格数量的增加而提高;对2025万网格算例,125核组(主从核合计8125核)并行计算加速约174 倍(相对于2 主核),众核(从核)并行加速7.9倍。
通过上述算例的测试与分析可见,对于三维不可压流动的非定常数值模拟,无论是MPI并行还是MPI++Athread多级并行,都能够获得相当可观的加速效果,说明了本文的并行计算方案在神威超算平台上的有效性。
3 三维方柱绕流大规模并行数值模拟与分析
鉴于前文中MPI+Athread的多级并行计算使并行加速比获得显著提升,将其用于大规模网格的非定常计算或能够显著提升计算速度。因此,采用直接数值模拟的方法,在神威异构超算平台上开展三维方柱非定常绕流数值模拟,柱体由图4 中长方形截面改为方形截面,截面边长同样为d且为特征长度,计算域扩大至A×B×C=24d×16d×10d。
Sakamoto 和Arie 等[8]研究发现,当方柱高宽比h/d>2 时,尾迹会形成交替脱落的涡即卡门涡街,反之则会形成对称脱落的拱形涡。本文针对h/d=4的情况,开展Re=250三维方柱绕流的CFD模拟,对瞬时流场、涡系结构、时均流场等进行分析,并与相关文献结果进行对比验证。
数值计算中,计算域大小为24d×16d×10d,方柱位于距入口6d处;数值计算采用了三套网格,网格单元数量分别为384万、3072万和24 576万(2.457 6亿);数值计算的网格划分、时间步长、计算资源和计算耗时等相关参数列于表5中。

表5 大规模并行数值模拟相关参数Tab.5 Parameters of massive parallel CFD computation
3.1 网格影响分析
虽然网格单元数量384 万已基本满足Re=250 三维方柱绕流的直接数值模拟要求,本文仍然通过三维倍增细化的方式(见表5),从宏观涡系结构、典型位置的时均速度分布和横向速度时历频谱分析等多个层面,进行数值模拟结果的网格影响分析。
(1)宏观涡系结构
图8 给出了根据Q判据(Q=0.01)得到的Re=250 三维方柱绕流涡系结构,其中图8(a)为384 万网格模拟结果,图8(b)为3072 万网格模拟结果,图8(c)为2.457 6 亿网格模拟结果。从图中可以看出三维方柱非定常绕流的典型特征:方柱与底面结合部前方形成马蹄涡;方柱自由端有大包络面的形成,表征自由端剪切层的分离;在方柱后方尾流区,形成了反对称的卡门涡。从图中同时可以看出,随着网格规模增加(空间分辨率增强),数值模拟获得的涡系结构更为丰富、精细。
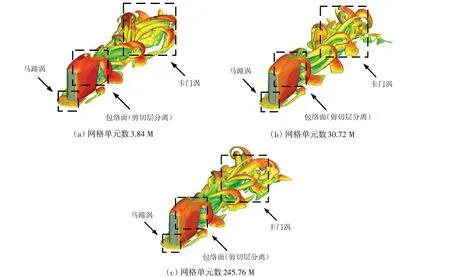
图8 Re=250三维方柱绕流涡系结构模拟结果Fig.8 Vortex system structure of flow past 3D square cylinder with Re=250
(2)时均速度的空间分布
为更好地分析网格空间分辨率对非定常三维方柱绕流时均流场的影响,取计算域中如图9 所示的a、b、c三条直线,分别比较线上的流向、横向、垂向时间平均速度分布。三条线的位置分别是:直线a平行于x轴,位于计算域的中纵截面上,距底面2.0d;直线b平行于y轴,位于距离方柱中心7.0d的垂直截面上,距底面3.5d;直线c则为距离方柱中心7.0d的垂直截面的垂直中心线。
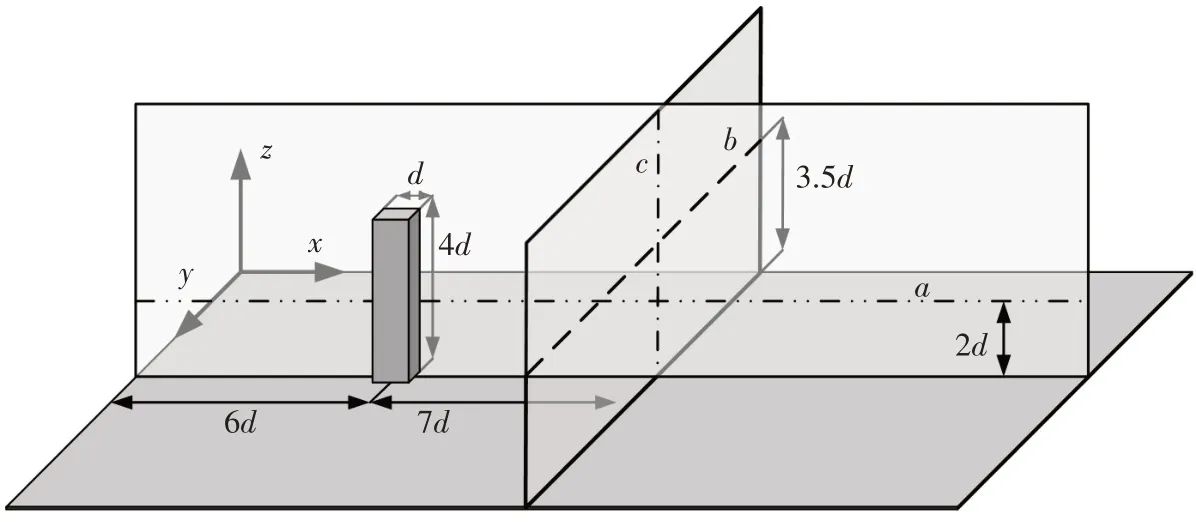
图9 时均速度对比分析位置示意图Fig.9 Locations of time-averaged velocities for caparison
图10~12 分别给出了a、b、c三条线上三套网格的流向、横向、垂向时均速度分布计算结果,图中同时给出了文献[9]的结果。从图中可以看出:对于三套网格,流向、横向和垂向时均速度计算结果均体现出与文献结果相同的空间分布特征;随着网格数量增加,横向和垂向时均速度随空间变化的波动幅度越大;3072 万网格和2.457 6 亿网格的计算结果与文献结果都较为接近,总体上3072万网格的计算结果与文献更为接近。

图10 直线a上流向时均速度计算结果Fig.10 Computational results of time-averaged stream-wise velocity on Line a
由此可见,在满足直接数值模拟要求的前提下,网格数量增加一方面会使数值模拟的宏观涡系结构更为精细,同时对时均速度的空间分布计算结果也有一定的影响。
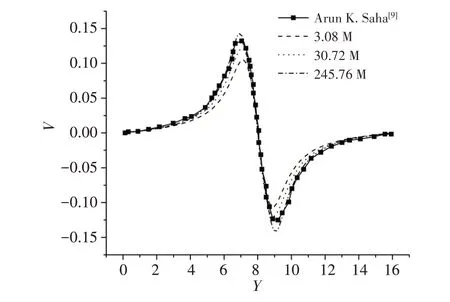
图11 直线b上横向时均速度计算结果Fig.11 Computational results of time-averaged transvers velocity on Line b

图12 直线c上垂向时均速度计算结果Fig.12 Computational results of time-averaged vertical velocity on Line c
(3)横向速度时历频谱分析
前面提到,本文研究的三维方柱绕流工况,尾迹会形成交替脱落的涡即卡门涡街,必然会导致尾迹中横向速度的振荡。为分析网格数量对方柱尾迹卡门涡街这一典型非定常流动特征数值模拟结果的影响,取方柱正后方A、B两个位置(如图13所示),对横向速度时间历程使用快速傅里叶分析(FFT)进行频谱分析和比较。A、B两点至方柱中心的距离分别为8.5d和15.5d,距底面皆为2.0d,都位于涡脱落影响区域内。
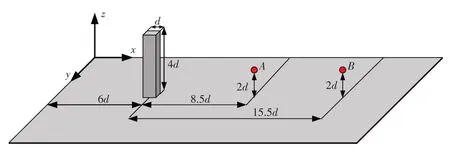
图13 横向速度时历频谱分析位置示意图Fig.13 Locations of time-history of transverse velocities for spectrum analysis
图14 给出了不同网格数量下方柱后A、B两点的横向速度时间历程数值模拟结果及其能量谱分析,其主频与幅值列于表6中。
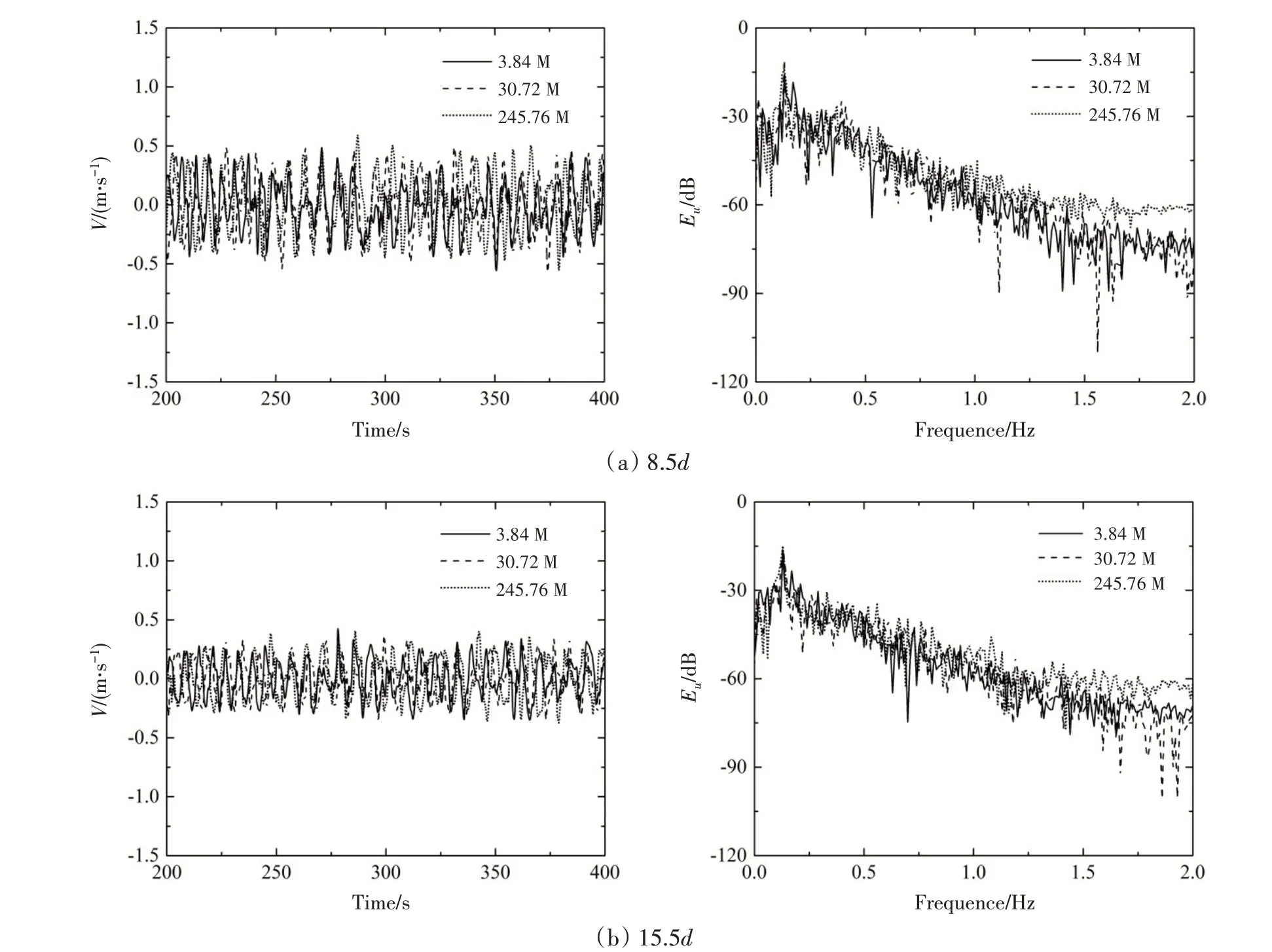
图14 方柱后方不同位置横向速度时历曲线及能量谱分析Fig.14 Time history and spectrum of transverse velocity at different locations behind the cylinder

表6 方柱后不同位置横向速度时历频谱分析结果Tab.6 Spectrum analysis of transverse velocity at different locations behind the cylinder
从图表中可以看出:随着网格数量增加,数值模拟得到的横向速度振荡主频略有增大,且网格数量大于3072 万后基本保持不变;而能量谱主频处峰值则随网格数量增加有所增大,且高频成分明显增强;此外,随着流向距离的增加,能量谱的峰值有所降低,反映了因粘性导致的能量耗散和衰减。
结合前面宏观涡系结构对比分析结果,说明本文使用的三套数量不同的网格,一方面都能够准确地模拟出三维方柱非定常绕流的涡脱现象和过程,另一方面网格数量增加能够更好地捕捉流场细节,特别是非定常流动中的高频成分。
3.2 流场模拟结果分析
综合以上网格数量对数值模拟结果影响的分析,接下来对三维方柱非定常绕流流场进行分析,重点针对3072万网格的数值模拟结果。以下从瞬时流场和时均流场两个方面,对Re=250三维方柱非定常绕流流场的数值模拟结果进行分析。
(1)瞬时流场分析
图15 给出了t=450 s 时刻以流向涡分量表征的涡系结构,与图8 中根据Q判据得到的涡系结构相比,能够更为清晰地看出方柱顶端的梢涡。由于方柱根部涡系结构复杂,在图8 和图15 中都难以观察到底层涡结构,不过在图17 的方柱后壁面流线图中,可以清楚地看到其根部由于底层涡形成的两个对称涡旋。

图15 瞬时x方向涡分量等值面涡系结构Fig.15 Instantaneous vortex system structure for x_vorticy
图16 为t=450 s 时刻计算域中纵截面(y/d=8.0)和水平截面(z/d=1.0)上的流线计算结果。从图中可以看出:水平截面上有明显的非对称涡的形成与脱落,与Sakamoto、Arie 等人的研究结果相符合;中纵截面上,在柱体前方,流动在此处分离,发生上冲和下洗;其中下洗流体在方柱与底面结合处回流,形成马蹄涡;上冲流体经方柱自由端发生分离,部分流体回流,在方柱后形成较大的回流区,延伸至方柱自由端处;同时在底部形成了反方向的回流区,且在回流下游靠近底面部分存在流线分离点即鞍点。
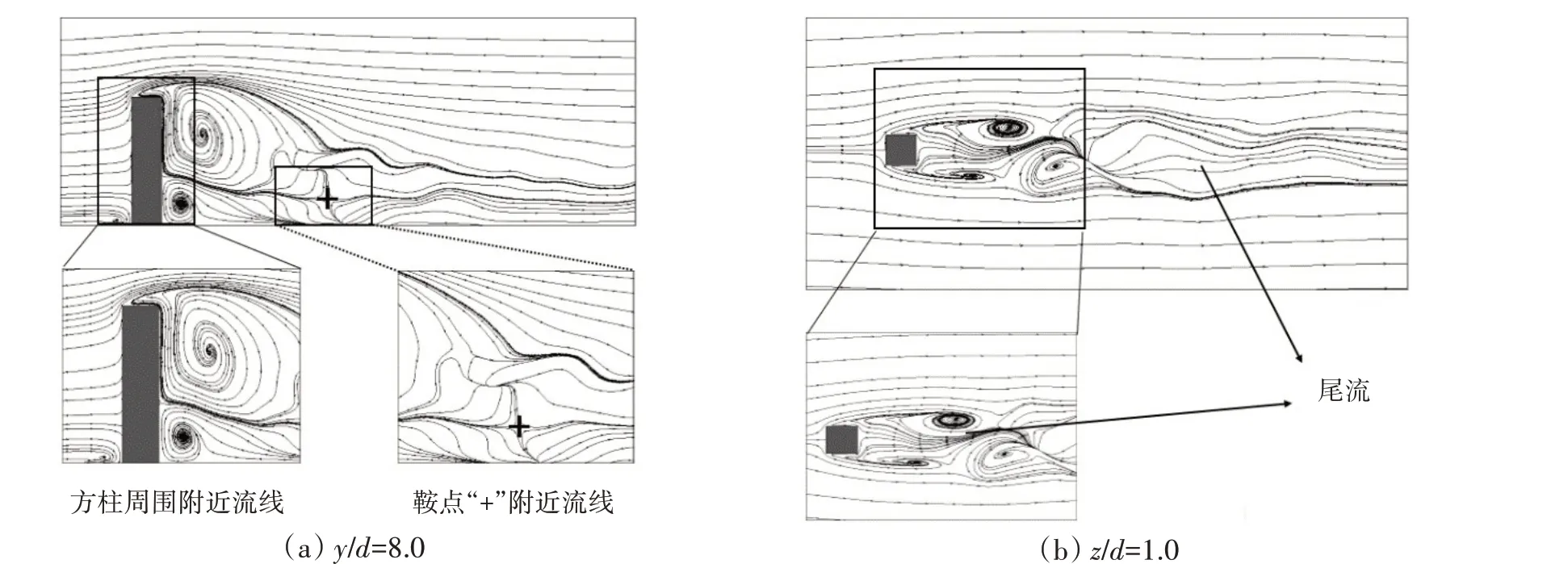
图16 Re=250三维方柱绕流流线计算结果Fig.16 Computational results of streamline of flow past 3D square cylinder with Re=250
图17为方柱前、后及侧壁的极限流线。从图中可以看出:在柱体前壁面有明显的滞流现象,流体在此处流向发生偏转并分离;在后壁面上,流动相较于前壁面更加复杂,可以看到存在一个奇点,流线均从该点发出,结合图16 所示中纵截面上的流线分布,后壁面上下流线的分离则表示方柱和后方形成的两个方向相反的回流区,并根据奇点位置,表明上升流仍然起主要作用,同时在底部可以看到一对底层涡;在侧壁面上有两组流线在此处相遇,且两组流线均存在上下分离现象,向下流动的流线进行汇聚,形成一个点,反映了底层涡的形成;向上流动的流体则汇聚成一条直线。
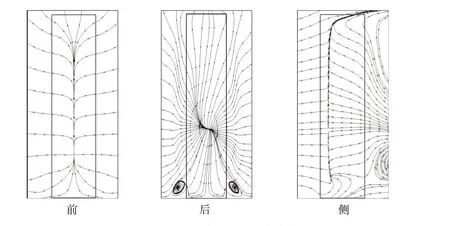
图17 方柱前、后、侧面流线计算结果Fig.17 Computational results of streamline on front,back and side faces of the square cylinder
图18为不同高度水平截面上Q准则涡量等值线,高度从0.2d到4.3d。图18(a)为底部附近截面上的涡量等值线,由于非滑移壁面的存在,底部的涡系结构非常复杂,但是可以明显地观察到柱体前方的马蹄涡;图18(b)中的涡量等值线则呈现出交替式的涡脱,但已不再是标准的卡门涡街分布,这表明自由端已经对中部的涡旋产生了影响;图18(c)-(e)则是方柱上部分以及顶面附近的涡量等值线图,可以看到随着高度向自由端靠近,卡门涡街越来越不明显,但是仍能观察到涡脱现象;同时在顶部附近可以观察到成对的梢涡,并向上倾斜,与图15中所示的梢涡形态相同。

图18 水平截面上Q准则涡量等值线图Fig.18 Q criterion vorticity contour on horizontal section
(2)时均流场分析
相较于瞬时流场的随机性,时均流场能够相对定量地反映流场中的一些典型特征。图19和图20分别给出了中纵截面(y/d=8.0)和水平截面(z/d=1.0)上时均流场的流线分布。
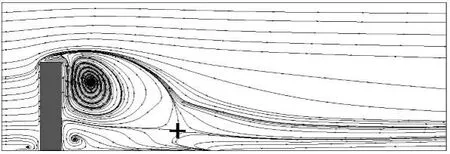
图19 Re=250三维方柱绕流中纵截面时均流线(y/d=8.0)Fig.19 Time-averaged streamline for flow past 3D square cylinder of Re=250 on y/d=8.0
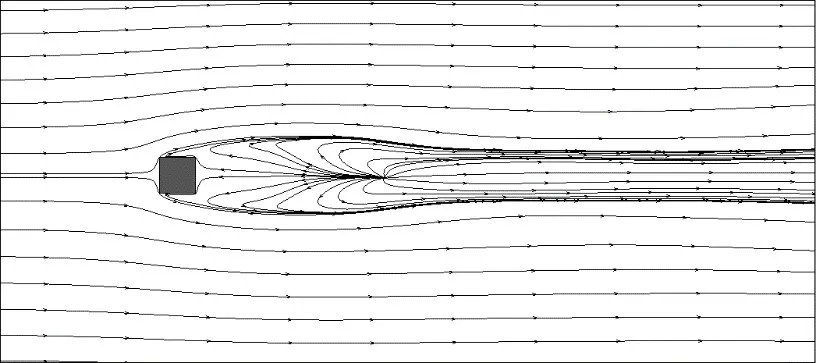
图20 Re=250三维方柱绕流中横截面时均流线(z/d=1.0)Fig.20 Time-averaged streamline for flow past 3D square cylinder of Re=250 on z/d=1.0
表7 则给出了上部回流区和根部回流区特征信息及其与文献结果的对比。由图表可以看出:图19 所示的水平截面上流线分布图中,柱体后方流线均从距离柱体中心约6d的奇点流出,并呈现对称状态,该奇点对应图18中的方柱后上冲和下洗的分离点鞍点“+”,奇点位置以及流线分布与文献[9]相当接近。

表7 方柱后回流区大小及位置信息Tab.7 Size and position of reflux zone behind the square cylinder
4 结 论
本文针对不可压缩流动常用的CFD 求解方法——SIMPLE 算法,开展了MPI+Athread 多级并行计算研究,并基于神威·太湖之光异构超算平台进行了三维方柱绕流的大规模并行数值模拟,最大网格数量达到2.46亿,并行规模达到13.3万核。通过对数值模拟结果的分析,可以得出以下结论:
(1)基于计算域区域分解和子区域内部循环分解的MPI+Athread 多级并行模式,能够使申威超算平台众核处理器的从核发挥较为可观的加速效果,加速比达到7.5~7.9 倍,且网格量越大加速效果越明显;
(2)在三维有限长方柱绕流的直接数值模拟中,采用MPI+Athread 多级并行,网格数量增加到2.46 亿,并行规模扩展到13.3 万核,可以将计算周期缩短至约160 小时,从而大幅度提升了CFD 大规模并行计算的能力;
(3)对于长径比为4、Re=250 的三维方柱非定常绕流,采用网格数量从384 万到2.46 亿进行直接数值模拟,对涡的脱落过程等宏观流动现象的模拟结果没有明显区别,不过网格数量增加能够更好地捕捉流场细节,模拟得到的涡系结构更为精细。
需要说明的是,本文的研究工作还是初步的,无论是MPI并行、众核并行还是MPI+Athread多级并行,都还存在优化和提升的空间;同时,本文的多级并行技术要应用到大型的CFD 计算程序/软件并达到实用化的程度,还有很多的研究和开发工作需要去做。这些也是论文研究团队接下来的重点工作。
