基于离散元法的立式旋耕刀工作参数分析与优化*
2022-09-21扈伟昊杨发展赵国栋林云龙黄珂
扈伟昊,杨发展,赵国栋,林云龙,黄珂
(青岛理工大学机械与汽车工程学院,山东青岛,266520)
0 引言
立式旋耕与传统卧式旋耕相比具有更深的作业深度、更大的作业幅宽和更快的作业速度,其可有效的破碎土壤、混匀前茬、降低犁底层高度、提高土壤蓄水保墒能力,具有耕后地表平整且不打乱耕层结构、一次耕作即可满足土壤播前要求、有利于抢农时等优点[1],这些优点使得立式旋耕在国家提倡保护性作业的背景下应用越来越多。立式旋耕作业过程中,立式旋耕刀的工作参数如前进速度、刀具转速、耕深对自身受力和作业效果有很大影响。
国内学者关于立式旋耕方面的研究多集中于立式旋耕机结构、刀具排列及耕后土壤性状对作物的影响等方面,而对立式旋耕工作参数的研究较少。刘芳建等就立式旋耕机的整机架构和刀片结构参数进行了分析,得到了不产生抗土现象时刀具内折弯角的临界值;张敏等[2]发现旋耕刀72°等分角安装方式与常规90°等分安装方式相比运动轨迹相似,但受到的冲击载荷更小,整机受力更平稳,使用寿命更长;聂胜委等[3]研究了立式旋耕对土壤紧实度的影响,通过试验发现,立式旋耕能降低小麦拔节期、灌浆期10 cm的土壤紧实度,同时立式旋耕处理的小麦连续两年产量增幅都较大,氮肥的农学效率和偏生产力均有显著提升。离散元法(discrete element method, DEM)是一种适用于不连续介质力学行为预测的方法,其最初应用于岩石边坡的运动分析,经过数十年的发展已广泛应用于各个领域[4-6]。国内外学者利用离散元法对农机作业过程进行了广泛的研究[7]。例如,熊平原等[8]用离散元法对卧式旋耕刀作业过程中所受三项阻力及扭矩进行了仿真分析,通过后期土槽试验对比发现,仿真得到的数据与试验得到的数据变化趋势相同;邓佳玉[9]使用EDEM对深松铲作业过程的受力情况进行仿真分析,结果表明仿真值与试验值相差在5%~15%;Ucgul等[10]通过离散元法模拟了板形犁耕作过程中的受力情况,得到了离散元法相较于解析法更加精确的结论;Makange等[11]利用EDEM软件建立了土壤—农具间的交互模型,该模型可以精确的模拟板形犁的切削力,由此可见,众多学者的研究都表明离散元法于农业机械作业过程研究的适用性。
本文旨在利用离散元法研究立式旋耕刀在不同前进速度、刀具转速、耕深条件下,刀具所受阻力、扭矩及其作业功率和其碎土效果;设计正交试验得到立式旋耕作业参数的系列预测模型,并利用所得预测模型综合旋耕机作业功率与碎土率,优化立式旋刀的工作参数。
1 立式旋耕作业模型建立
1.1 立式旋耕刀建模
立式旋耕刀是立式旋耕的作业部件,其结构参数对作业效果及机具整体性能影响很大,本试验采用的旋耕刀其参数的设置如表1所示。
使用SolidWorks2018软件建立立式旋耕刀的三维模型如图1所示,将模型文件保存为.igs格式。

表1 立式旋耕刀的参数设置Tab. 1 Parameter setting of vertical rotary tiller blade
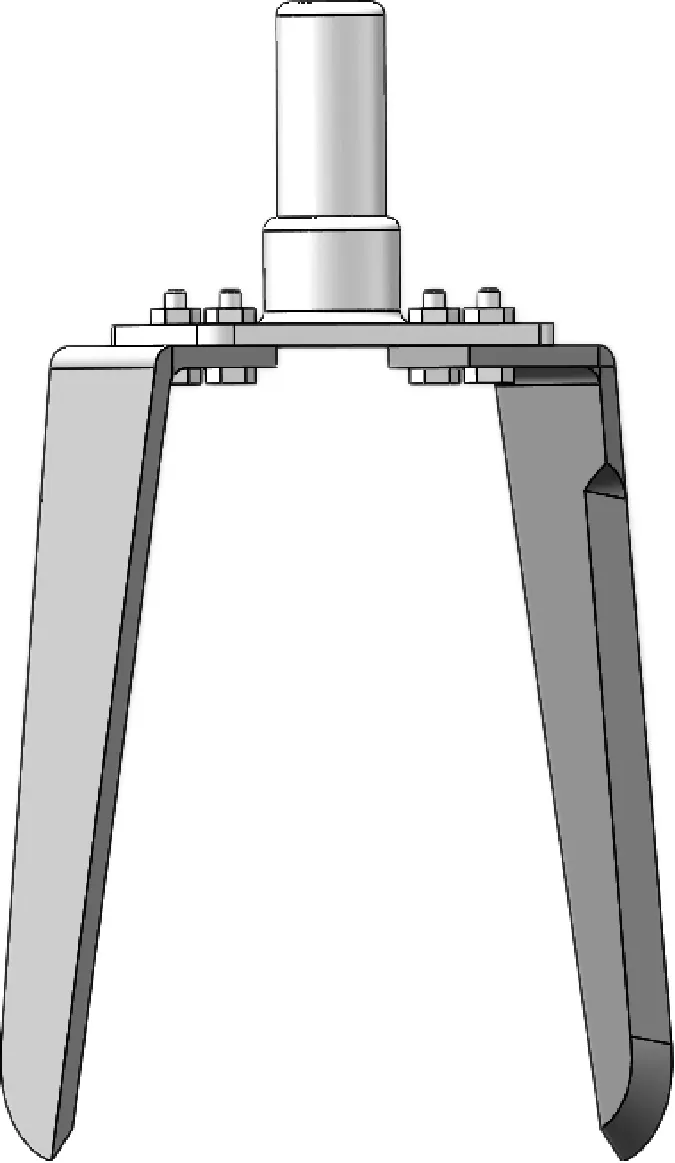
图1 立式旋耕刀的三维模型
1.2 土槽模型建立
1.2.1 土壤颗粒模型的建立
为探究土壤颗粒的性质,于胶东地区农田采集土样,通过电子显微镜观察发现土壤颗粒呈现不规则的球形及三角片状,因此本试验采用图2所示的球体和三球组合颗粒模拟真实土壤颗粒,为减少仿真运算量,将球体颗粒和三球组合颗粒中球体半径放大至5 mm。
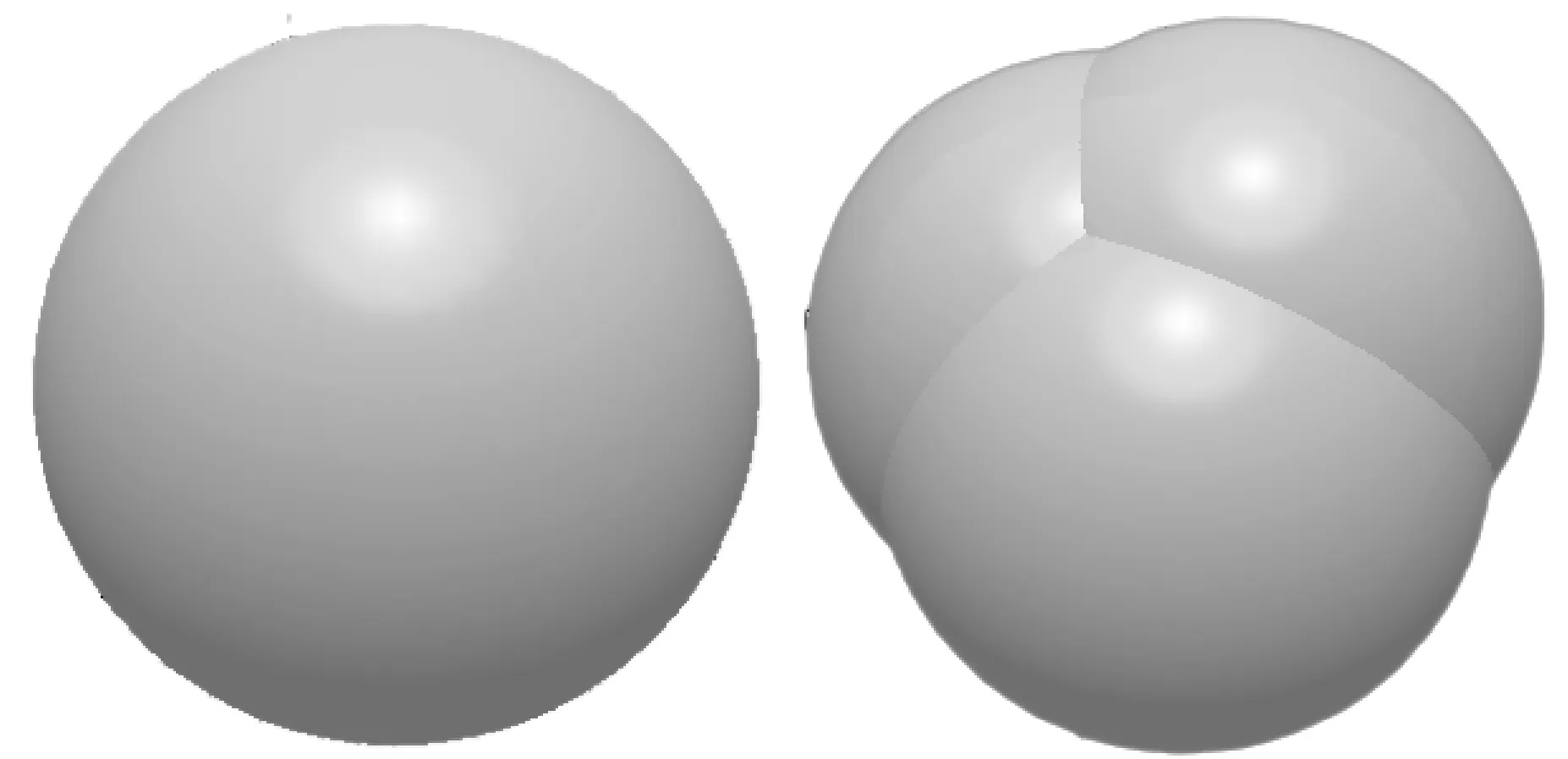
图2 球形颗粒与三球组合颗粒
1.2.2 接触模型的选择
EDEM软件中内置了Hertz-Mindlin(no slip)、Hertz-Mindlin with Bonding、Hertz-Mindlin with JKR等接触模型,其中Hertz-Mindlin with Bonding、Hertz-Mindlin with JKR都可应用于土壤颗粒间的约束[12-13]。通过土壤质地分析试验得到本试验中土壤平均含水率17.94%,宜选用Hertz-Mindlin with Bonding模型模拟土壤颗粒间的粘结[8]。该模型在颗粒之间形成粘结键以承受一定的阻力和阻力矩,粘结键产生之后,颗粒上的法向力Fn、切向力Ft与法向力矩Tn、切向力矩Tt从0随时间步按照式(1)调整。
(1)
式中:δ——时间步长;
vn——颗粒法向速度,m/s;
vt——颗粒切向速度,m/s;
Sn——颗粒法向刚度,N/m;
St——颗粒切向刚度,N/m;
ωn——颗粒法向角速度,rad/s;
ωt——颗粒切向角速度,rad/s;
A——颗粒接触面积,m2;
J——颗粒惯性矩,m4;
RB——颗粒间粘结半径,m。
粘结键所受法向力与切向力达到临界值时断裂,其临界法向、切向应力如式(2)所示。
(2)
式中:Mτ——颗粒间切向力矩;
Fτ——颗粒间切向力;
Mn——颗粒间法向力矩。
1.2.3 参数设置
离散元仿真参数包括材料本征参数、材料接触参数和接触模型参数,其中材料本征参数包括材料泊松比、密度、剪切模量(或杨氏模量);材料接触参数包括恢复系数、静摩擦因数、动摩擦因数;Hertz-Mindlin with Bonding接触模型参数包括法向刚度、切向刚度、临界法向应力、临界切向应力及粘结半径[14-15]。本试验中立式旋耕刀材料选为65 Mn,通过查阅相关文献[16-18],确定离散元仿真的具体参数如表2所示。
在EDEM前处理模块中创建材料及颗粒,并按表2设置好参数后,建立尺寸为2 000 mm×500 mm×400 mm的土槽,土槽中土壤的高度为27 cm,其中由上至下0~16 cm为耕层土壤,16~27 cm为犁底层土壤,土槽模型如图3所示。
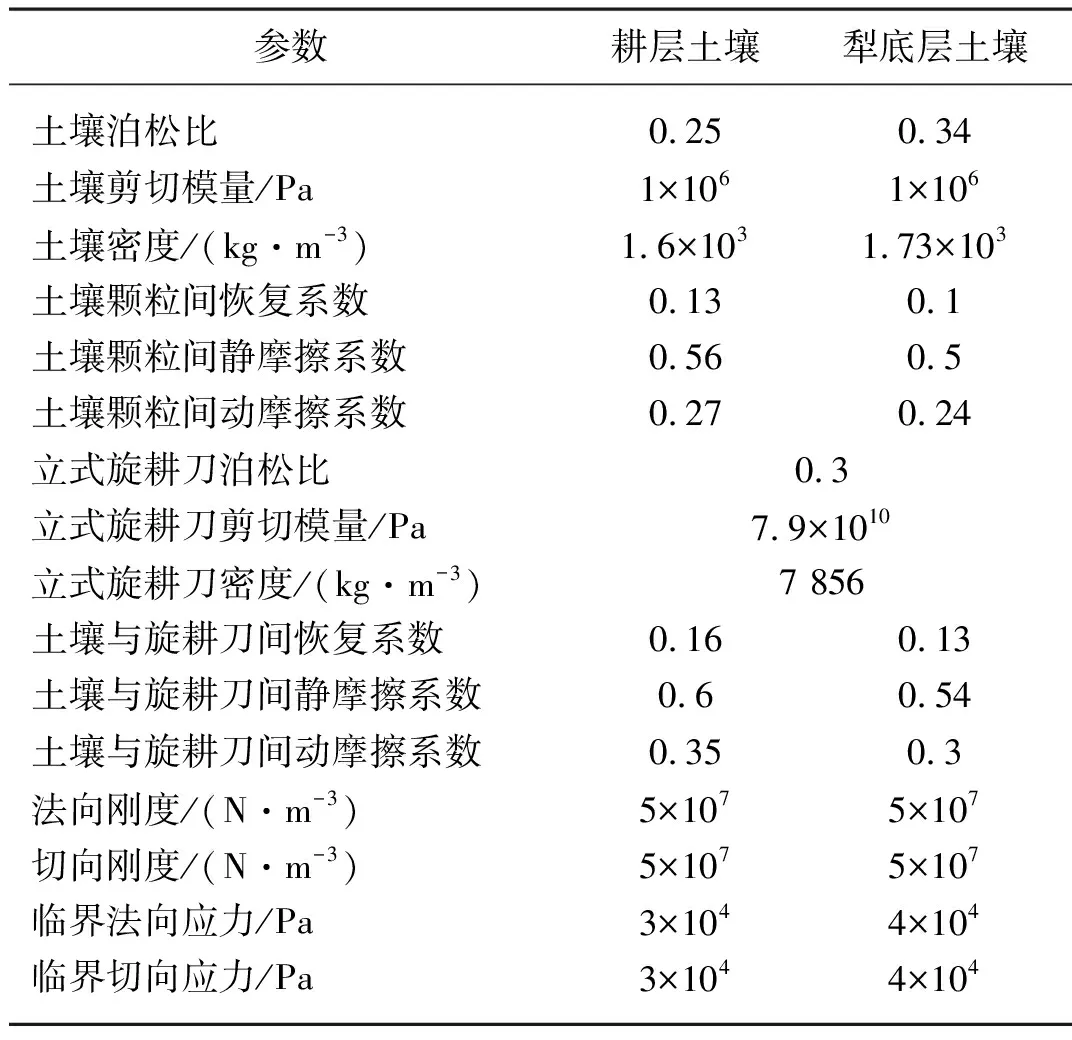
表2 仿真模型参数设置Tab. 2 Simulation model parameter settings

图3 土槽模型
2 旋耕作业仿真分析
2.1 仿真过程
设定立式旋耕刀的前进速度为1.5 m/s,刀具转速300 r/min,耕深25 cm。设定仿真总时长为1.25 s,其中0~0.25 s为刀具入土时间,0.25~1.25 s为旋耕作业时间,仿真过程如图4所示。



(a) 0.00 s (b) 0.25 s (c) 0.50 s



(d) 0.75 s (e) 1.00 s (f) 1.25 s
2.2 旋耕作业阻力分析
定义立式旋耕刀受到阻力的方向,如图5所示,设Fx、Fy、Fz分别为立式旋耕刀所受前进阻力、侧向阻力与垂直阻力,以刀具前进方向为前进阻力Fx的正向,垂直于前进方向向内为侧向阻力Fy的正向,竖直向上为垂直阻力Fz的正向。对0.44~0.66 s立式旋耕刀的阻力进行分析,作旋耕刀所受总阻力与三向阻力值随时间的变化图,如图6所示。
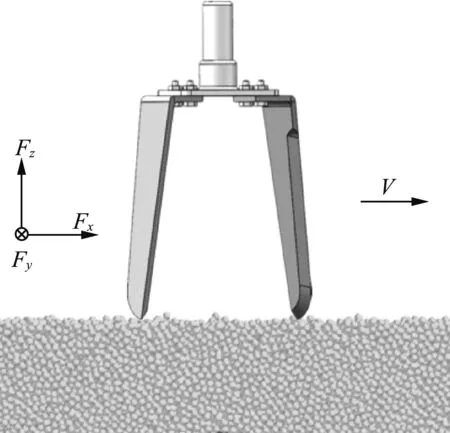
图5 立式旋耕刀三向阻力方向定义
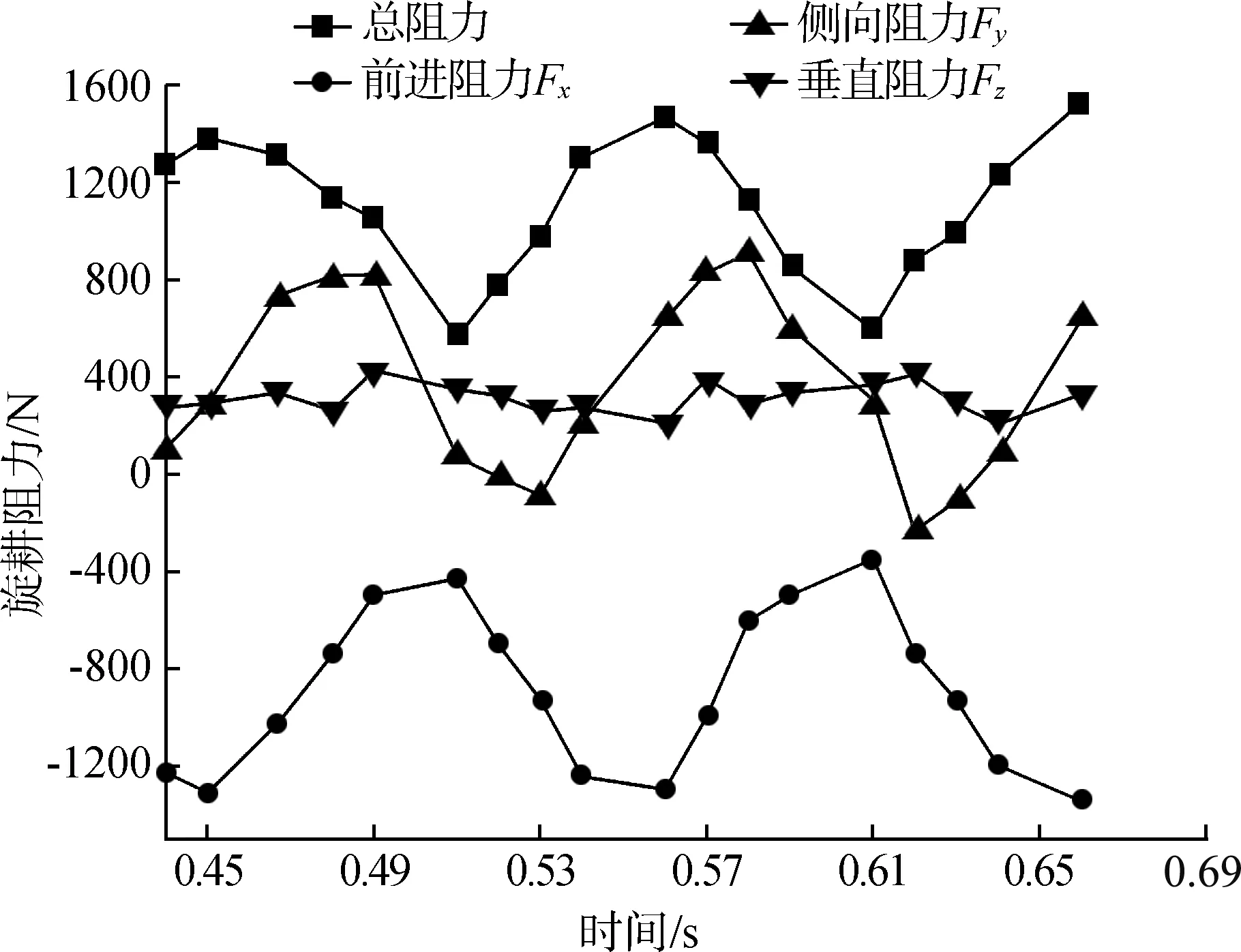
图6 旋耕刀所受阻力随时间的变化
其中0.45~0.65 s为旋耕刀进入作业阶段的第二个转动周期,由图5可知:旋耕刀前进阻力Fx始终为负值,这表明在整个旋耕周期内旋耕刀的前进阻力与前进方向相反;旋耕刀所受前进阻力与总阻力变化趋势相同且同时达到峰值和谷值,这表明旋耕作业过程中前进阻力对总阻力的变化趋势影响较大。侧向阻力Fy与前进阻力Fx的变化趋势相反,前进阻力达到峰值时,侧向阻力在谷值附近,前进阻力达到谷值时,侧向阻力达到峰值附近。旋耕刀垂直阻力Fz则在整个旋耕作业过程中处于相对稳定的状态,并在300 N左右上下浮动。
在一个周期内,旋耕刀总阻力的峰值为1 374.79 N、1 460.10 N分别在0.45 s、0.56 s时刻出现,谷值为557.756 N、587.248 N,在0.51 s、0.61 s时刻出现。旋耕刀总阻力达到峰、谷值时所处位置如图7所示。


(a) 0.45 s (b) 0.56 s


(c) 0.51 s (d) 0.61 s
由图7(a)、图7(b)可知,当旋耕刀总阻力为峰值时,其位于机具8刀具前进方向上的未耕区域,土壤质地坚硬,旋耕刀受到切削土壤、破坏土壤结构与土壤颗粒时的阻力;当旋耕刀总阻力为谷值时,其位于如图7(c)、图7(d)所示的已耕区域内,土壤质地疏松,旋耕刀只受到扰动土壤颗粒的阻力[18-19]。
2.3 旋耕刀所受扭矩分析
旋耕作业中,旋耕刀受到的扭矩是一项重要的工作指标,通过扭矩的变化情况可以判断旋耕刀整体工作的稳定性。本试验中,旋耕刀扭矩随时间的变化情况如图8所示。
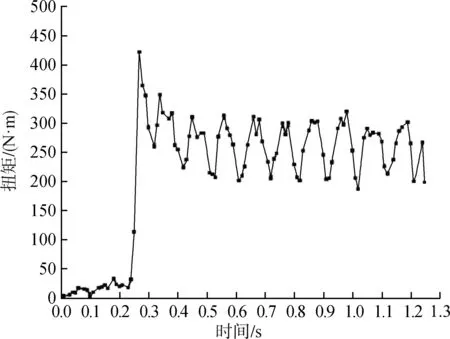
图8 旋耕刀所受扭矩随时间变化情况
从图8可以看出,0~0.25 s,随着刀具入土深度的增加,其所受扭矩在波动中略有上升,0.25 s后扭矩骤升,在0.27 s达到峰值421.86 N·m。旋耕作业稳定后,旋耕刀所受扭矩在约200~310 N·m间波动,其周期与变化趋势与旋耕总阻力相似。
3 正交试验的设置与分析
3.1 试验方案与结果
立式旋耕作业过程中机具的前进速度、刀具转速及耕深影响着刀具自身受力和作业效果,为对上述三个工作参数进行分析优化,以旋耕刀所受阻力、扭矩及作业功率和碎土率为评价指标,使用Design-Expert 12软件设计多因素正交试验,试验的因素水平编码如表3所示。正交试验设计方案及试验结果如表4所示。
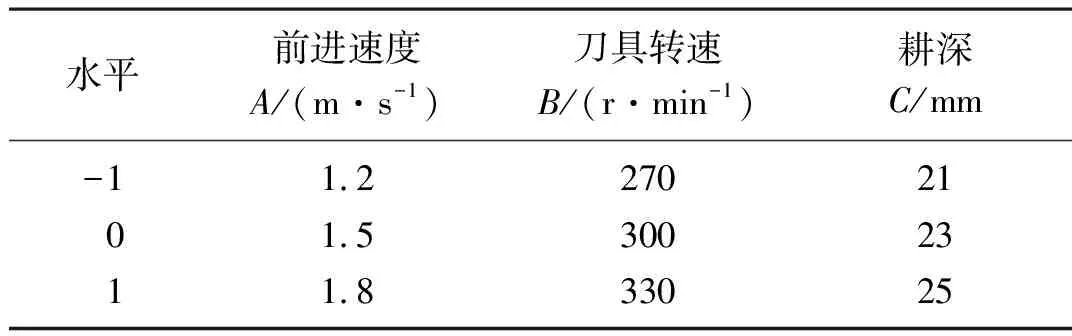
表3 仿真试验因素水平及编码Tab. 3 Factor levels and coding

表4 正交试验结果Tab. 4 Orthogonal test results
表4中,旋耕刀所受阻力、扭矩取立式旋耕刀作业稳定后2个旋转周期的平均值,碎土率取旋耕刀作业相同距离(1.2 m)时Bond键的破碎率,作业功率通过式(3)计算得出。
(3)
式中:P——作业功率,kW;
T——扭矩,N·m;
n——刀具转速,r/min。
3.2 方差分析与回归模型建立
3.2.1 旋耕刀所受阻力的回归模型与方差分析
通过Design-Expert 12数据处分析,得到阻力F的拟合回归方程如式(4)所示。
F=930.62+120.4A-37.84B+135.7C+
32.51AC-49.98C2
(4)
回归模型的方差分析结果如表5所示。
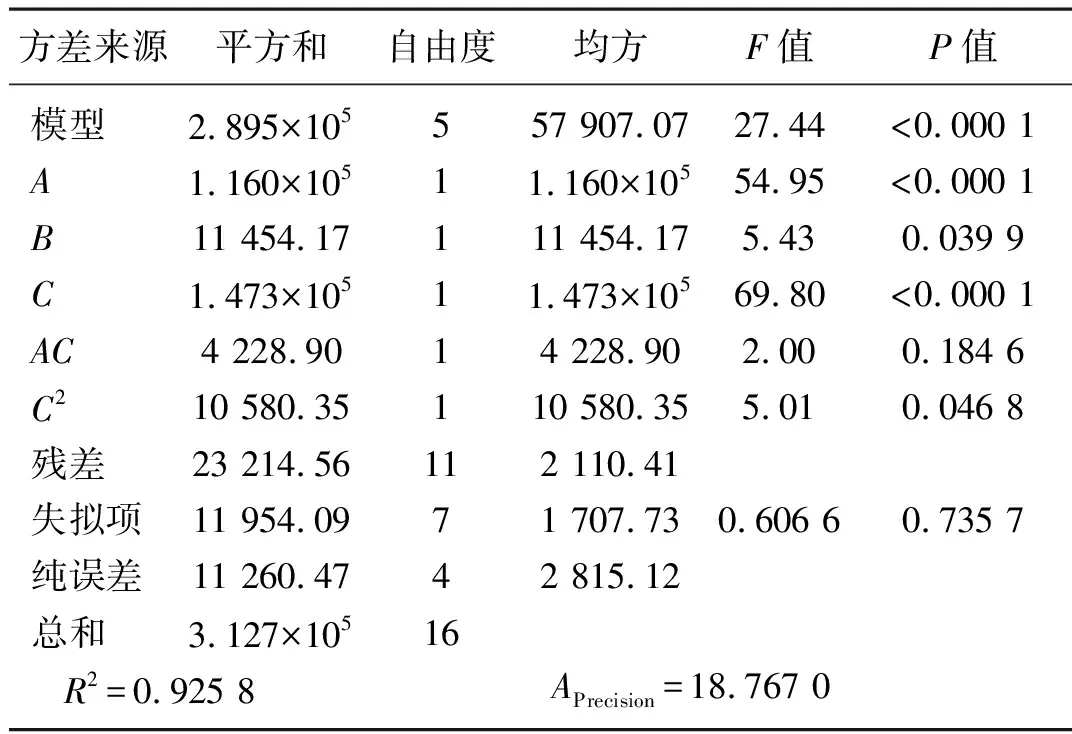
表5 旋耕刀所受阻力回归模型的方差分析Tab. 5 Variance analysis of rotary tillage resistance regression model
从表5可以看出,该回归模型的P值小于0.000 1,表明该模型具有很高的显著性,模型的失拟向P值与F值均大于0.05,拟合精度较高;模型的多元系数R2为0.925 8,表明模型的相关性较好;信噪比APrecision为18.767 0,远大于4,说明该模型具有较高的可信度与准确度,通过各参数P值对比发现,前进速度A与耕深C对阻力的影响最为显著,其次是刀具转速B,二阶耕深C2再次之,前进速度与耕深的交互项AC对阻力的影响最小。
3.2.2 旋耕刀所受扭矩的回归模型与方差分析
通过数据分析,得到旋耕刀所受扭矩T的回归方程如式(5)所示。
T=241.13+24.32A-5.68B+25.42C+
8.36AC-11.29C2
(5)
该回归模型的方差分析结果如表6所示,其P值为0.000 2小于0.05,表明该模型显著性较高;模型的失拟项P值为0.830 4大于0.05,F值为0.452 7亦大于0.05,表明模型失拟性不显著,误差较小,拟合程度高;多元系数R2为0.863 1,说明模型中变量的相关性较好,模型的信噪比APrecision为13.309 5,可靠性较高。通过对参数的P值、F值分析可知,各参数中耕深对扭矩的影响最为显著,其次是前进速度和二阶耕深,而刀具转速、前进速度与耕深的交互项对扭矩的影响均不显著(P>0.1)。

表6 旋耕刀所受扭矩回归模型的方差分析Tab. 6 Variance analysis of rotary torque regression model
3.2.3 作业功率的回归模型与方差分析
通过数据分析,得到作业功率P的多元拟合回归方程如式(6)所示。
P=7.57+0.771 3A+0.566 3B+0.787 5C+
0.217 5AB+0.26AC-0.381 9C2
(6)
该回归模型的方差分析结果如表7所示,该回归模型的P值为0.000 3远小于0.05,表明该模型极为显著;对模型进行失拟项检验,其P值为0.783 2,F值为0.505 1均大于0.5则模型失拟性不显著,拟合程度较高;多元系数R2为0.888 2,信噪比APrecision为12.484 0,表明该回归模型具有较高的精确度与可靠性。通过对各参数的F、P值分析可知,立式旋耕刀的前进速度、刀具转速、耕深对作业功率的影响都极为显著,二阶耕深显著,各交互项则不显著(P>0.1)。
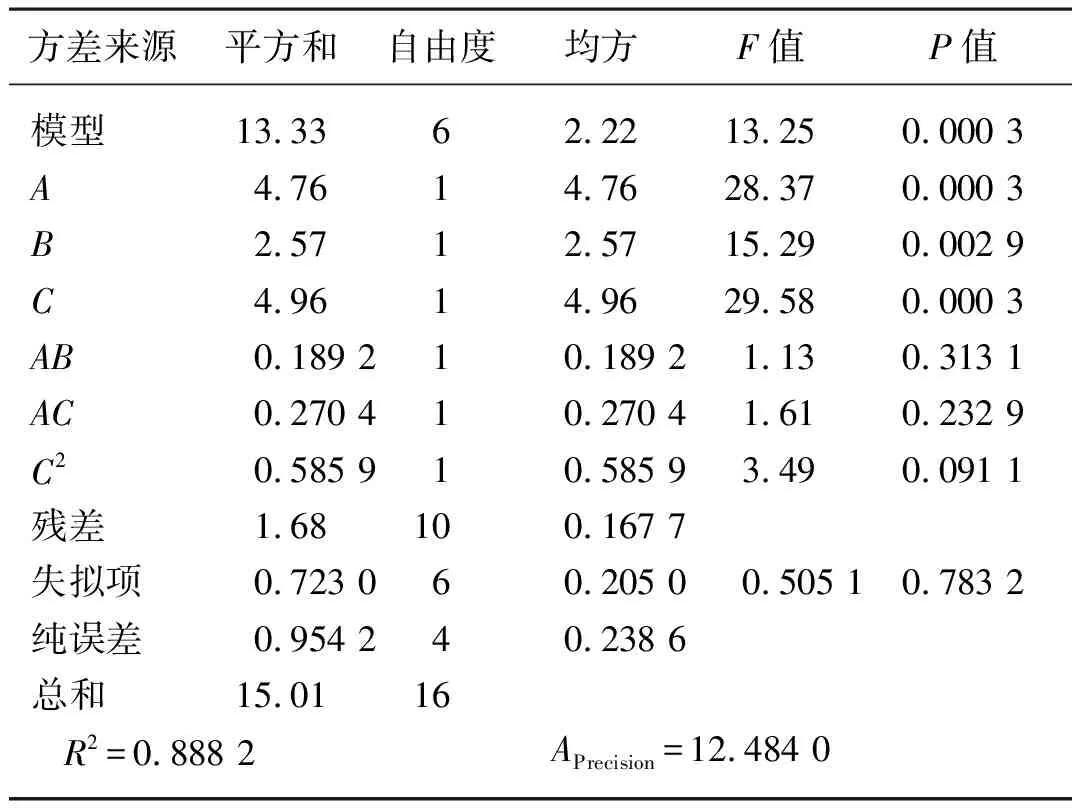
表7 作业功率回归模型的方差分析Tab. 7 Analysis of variance of power regression model
3.2.4 碎土率的回归模型与方差分析
通过数据分析,得到碎土率W的多元拟合回归方程如式(7)所示。
W=67.15-2.21A+1.74B+8.03C+
2.11BC+1.41A2+1.13C2
(7)
回归模型的方差分析如表8所示。
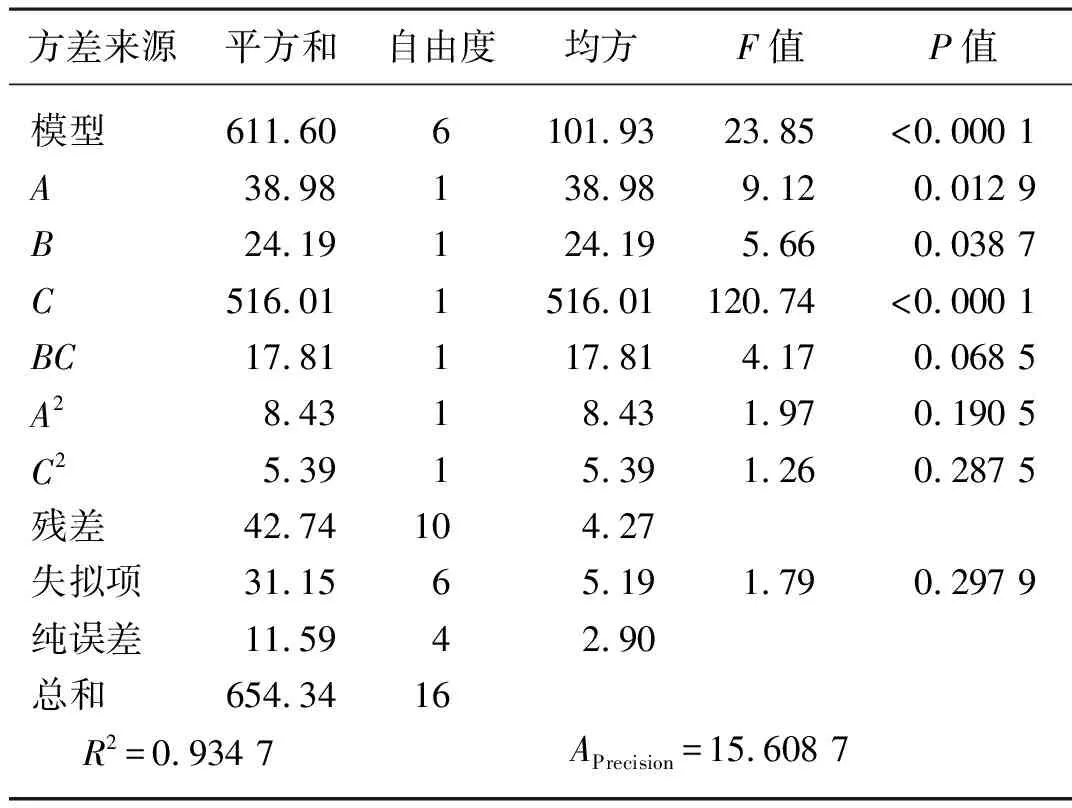
表8 碎土率回归模型的方差分析Tab. 8 Analysis of variance of regression model of broken soil rate
从表8可以看出,该回归模型的P值小于0.000 1,表明该回归模型极为显著;模型的失拟项系数F值与P值皆大于0.05,表明该模型的失拟性不显著,拟合精度较高;模型的多元系数R2为0.934 7,表明模型具有相关性,信噪比APrecision为15.608 7远大于4,表明该模型具有较高的可信度。对参数的P值、F值分析得到各参数对碎土率影响的显著性为耕深>前进速度>刀具转速>转速与耕深的交互项BC>二阶前进速度A2>二阶耕深C2。
3.3 各因素的响应面分析
通过Design-Expert 12软件对数据的处理,得到工作参数对旋耕刀所受阻力、扭矩及作业功率和碎土率影响的响应面图如图9~图12所示。
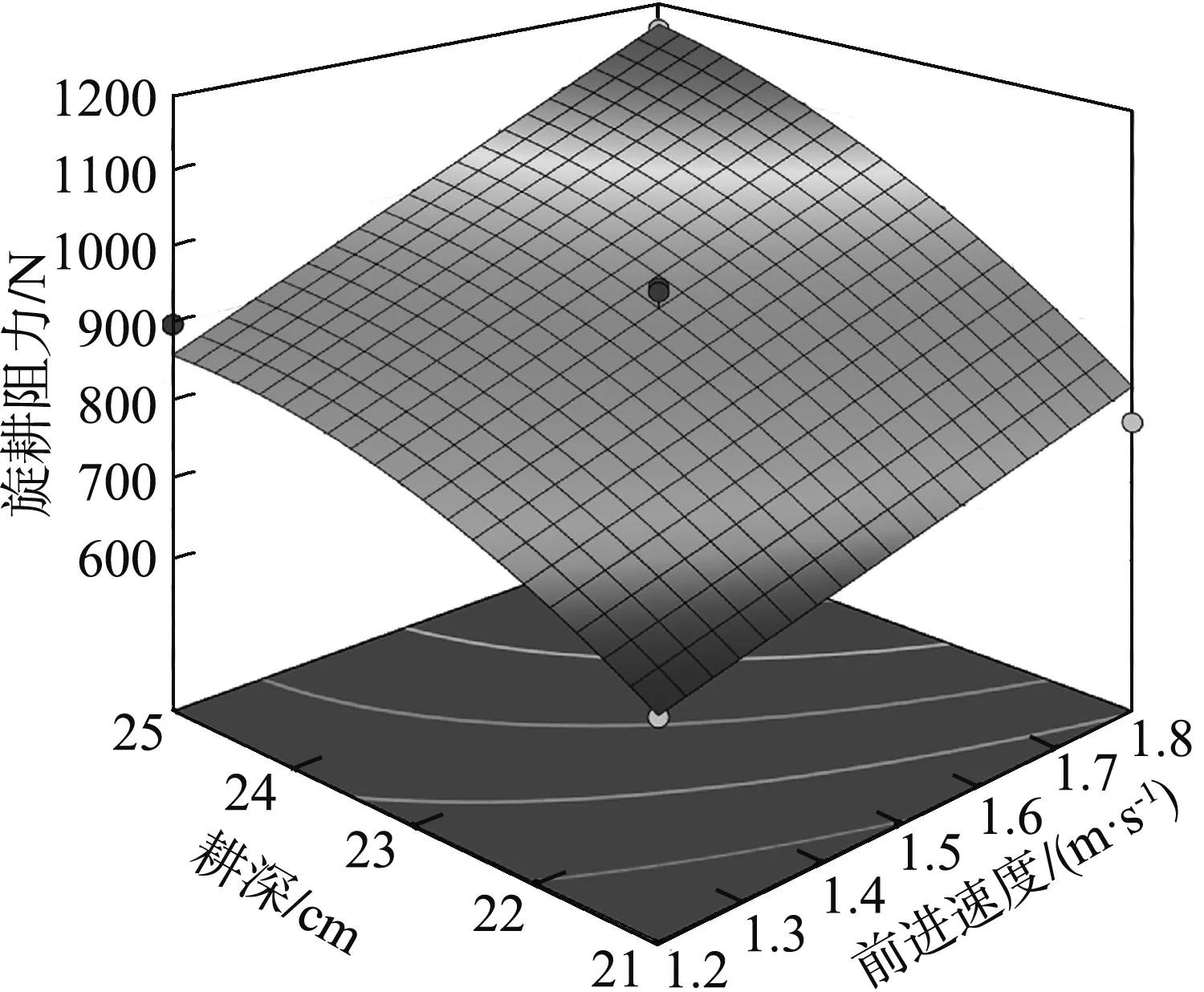
图9 各因素对旋耕刀所受阻力的响应面图
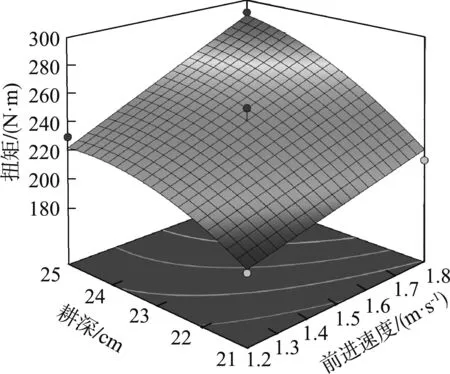
图10 各因素对旋耕刀所受扭矩的响应面图
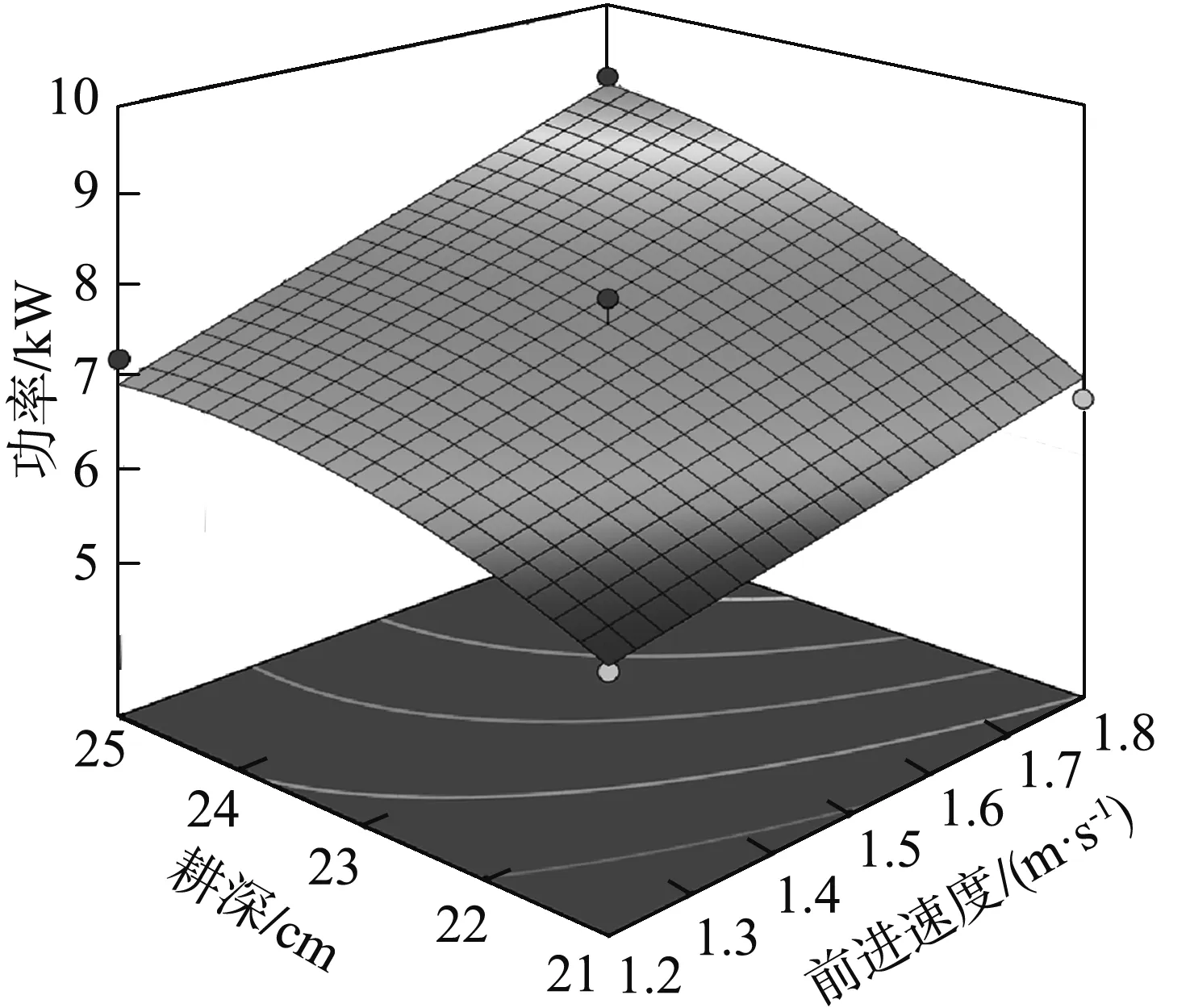
图11 各因素对旋耕刀作业功率的响应面图

图12 各因素对旋耕刀碎土率的响应面图
从图9可知,随着前进速度、耕深的增加以及刀具转速的减小,旋耕刀所受扭矩呈现增加的趋势,在耕深加深的过程中,阻力的增加速率逐渐减小;较浅的耕深与较慢前进速度可得到较小的前进阻力。由图10可知,扭矩随各因素的变化情况与阻力相近。由图11可知,前进速度、刀具转速、耕深与扭矩都呈正相关;较浅的耕深与较小的前进速度可得到较小的作业功率。由图12可知,耕深及刀具转速的增加会带动碎土率的增加,但增加刀具转速对碎土率的提升效果并不明显,而刀具的前进速度与碎土率呈负相关;较深的耕深及较快的刀具转速会带来较高的碎土率。
3.4 参数优化
利用Design-Expert软件的优化模块,通过所得预测模型对立式旋耕刀的作业功率和碎土率进行综合优化,其约束及目标函数如式(8)所示。
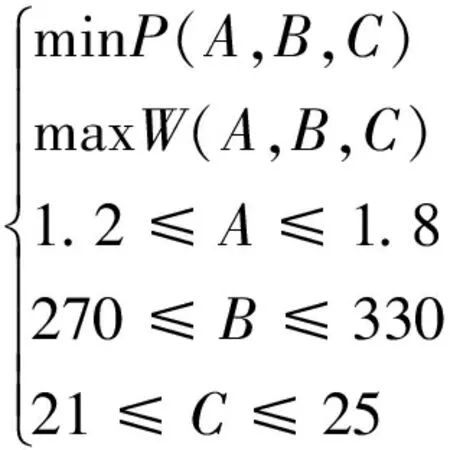
(8)
得到的最佳工作参数:前进速度为1.2 m/s,刀具转速为307.141 r/min,耕深为25 cm,此时模型预测的立式旋耕刀作业功率为7.042 kW,碎土率为80.85%,将上述参数带入仿真试验,得到模型预测值与仿真值的作业功率相对误差为3.97%,碎土率相对误差为3.45%,验证了预测模型的可用性。
4 结论
1) 建立了立式旋耕刀作业过程的离散元模型,通过仿真试验对立式旋耕刀作业过程中各向阻力及扭矩的变化情况进行了简要分析。
2) 通过设计正交试验得到立式旋耕刀所受阻力、扭矩及作业功率、碎土率随旋耕刀前进速度、刀具转速、耕深的变化规律,并建立相应的多元回归预测模型。
3) 利用所得预测模型对立式旋耕作业参数进行优化,得到的结果为:前进速度1.2 m/s,刀具转速307.141 r/min,耕深25 cm,此时立式旋耕刀的作业功率为7.042 kW,碎土率为80.85%,经过仿真验证得到作业功率模型预测值与仿真值的相对误差为3.97%,碎土率相对误差为3.45%,这表明了在一定的误差允许范围内预测模型的可用性。
