MVC850B型立式数控铣床误差分析与补偿试验研究
2022-09-21薛邵文
薛邵文
(1.泸州职业技术学院智能制造与汽车工程学院,四川泸州 646005;2.四川省泸州市智能制造重点实验室,四川泸州 646005)
0 前言
如今的制造业中,随着复杂参数曲面加工精度的要求不断提高,高性能精密三轴联动数控铣床得到广泛应用和迅速发展。加工精度是衡量数控铣床工作性能的重要指标,但是由于铣床在组装、控制及运动过程中受到各种因素的综合影响,其精度严重衰减,对零件的精密加工造成了极大影响,从而影响整个产品的生产质量和效率。因此,通过误差补偿技术来提高数控铣床加工精度的稳定性一直是现代制造领域的一个重要研究方向,很多学者对此深耕多年。郝惠东对数控铣床进行模态分析,根据分析结果构建齿面方程,对数控铣床加工误差进行计算后构建误差修正模型。熊青春等利用机床精度检测数据和零件特征及其工艺参数构建评估指标体系,基于BP神经网络建立了飞机结构件加工误差预测模型,实测结果和模型数据吻合。杨祥等人在华中8型数控系统中,应用HIO-1075温度采集板卡,嵌入热偏置补偿和斜率补偿模块,实时监测温度变化,对机床运动部件的热位移误差进行实时补偿,该模块已批量装机使用,并得到用户认可。于海祥提出一种基于多层感知器(MLP)神经网络的误差补偿方法,试验结果表明,该方法能够对加工误差进行精确补偿,具有有效性和可行性。
本文作者应用Renishaw XL-30激光干涉仪对MVC850B数控铣床的定位误差进行精密检测试验。首先,利用环境参数对比试验,得出空气温度、空气湿度和大气压力对定位误差测量的影响;然后,利用三因素双指标正交试验判断进给速度、加工时间以及测量时的测距各输入变量等单因素影响下反向间隙与螺距累积误差的主次关系;再次,通过单因素对比试验获得反向间隙与螺距累积误差在某个单因素影响下的变化情况及影响定位精度的原因;最后,采用半闭环前馈补偿方式对数控铣床定位误差进行补偿,并进行工件加工验证试验。
1 定位误差测量试验系统
试验研究设备是某学院金工实训车间的MVC850B型三轴立式数控铣床,具体参数如表1所示。

表1 MVC850B数控铣床参数
用英国Renishaw制造的XL-30激光干涉仪对MVC850B数控铣床的定位误差进行精密检测。定位误差测量系统由激光干涉仪、数据采集卡和计算机等组成。数控铣床定位误差测量系统如图1所示。每次测量前,使室内试验温度保持在(20±0.5)℃,并先启动铣床空运行2 h,消除温度变化对铣床误差的影响,使它达到相对平衡状态。为使激光干涉仪激光频率达到稳定状态,需将激光器预热约20 min,尽量减小周围环境的振动和干扰源。

图1 MVC850B数控铣床定位误差测量系统
Renishaw XL-30激光干涉仪主要包括激光器、补偿单元、线性测量光学镜、三脚架等,主要性能参数如表2所示,其误差检测原理如图2所示。激光器发射激光束1经分光镜分解成反射光束2和发射光束3,然后光束2和光束3又分别经反射镜送回分光镜调制,最后把光束4传回激光器中,激光反射器依据光束2和光束3在Renishaw XL-30中产生的明暗干涉条纹数获得反射镜到激光发射器之间的实际距离,并最终传送到计算机中获得误差数据。
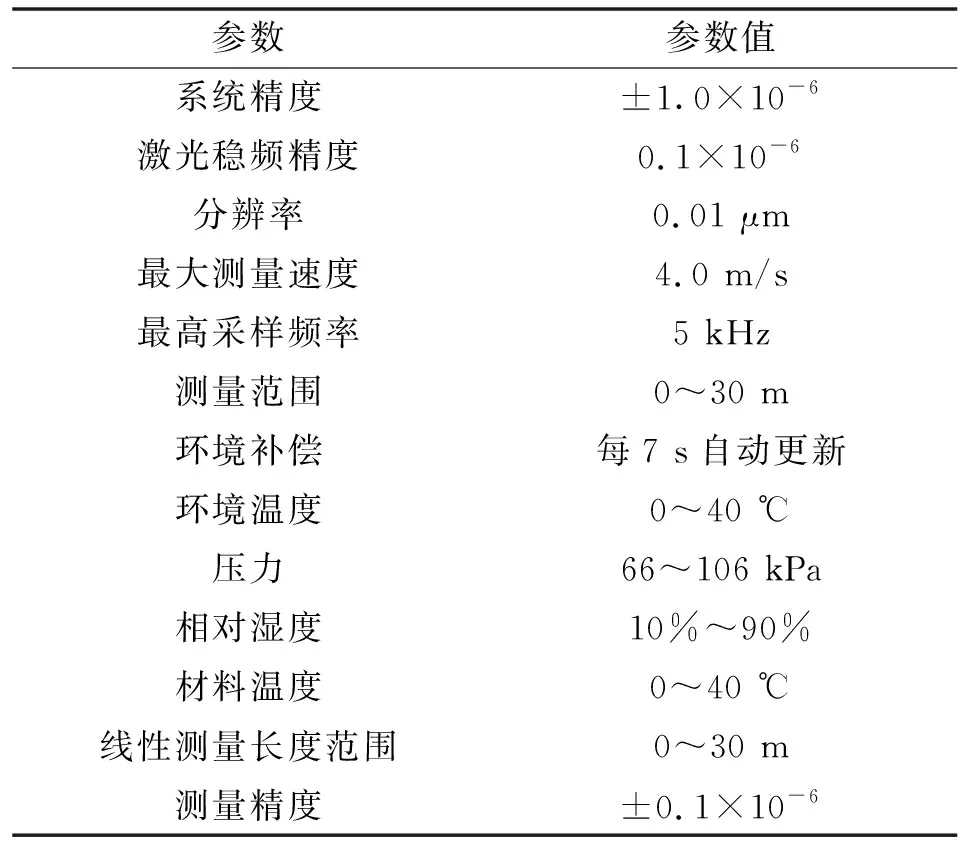
表2 Renishaw XL-30激光干涉仪性能参数

图2 激光干涉仪定位误差检测原理
2 误差测量试验与结果分析
2.1 环境参数对比试验
在铣床定位误差测量中,铣床的安装、激光干涉仪的使用和周围环境的影响都会造成测量结果的不准确。影响激光干涉仪测量精度的主要因素包括:环境误差、仪器精度、安装误差。环境因素主要是指空气温度、大气压力和空气湿度等,这些因素的叠加效果最终引起测量误差。环境因素造成的误差如式(1)所示:
=

(1)
式中:为气温;为气压;为湿度;为被测件温度;为线膨胀系数;=94×10、=028×10、=005×10。
仪器误差主要是由激光干涉仪本身的分辨率等造成,可用式(2)表示:

(2)
式中:δ为激光干涉仪电路部分误差,由于此电路一般精度很高,通常忽略其误差。因此,主要考虑激光波长误差δ。激光波长精度一般在10量级,故通常认为激光干涉仪精度可达0.1×10±1分辨率当量。
激光器和线性测量光学镜安装调试不准确会造成安装误差。当反射镜的运动轴线与测量轴线不重合时会产生阿贝误差;当被测对象的运动轴线与测量轴线不平行时会产生余弦误差;在调试线性测量光学镜时,镜间的距离会引起空气折射率的变化,造成死程误差。
综上所述,激光干涉仪的测量误差可用式(3)表示:

(3)
在实际测量试验中,Renishaw XL-30激光干涉仪的系统精度和分辨率基本能满足测量要求。阿贝误差可以通过减小阿贝臂消除;余弦误差可以通过调整激光器的偏转角消除;死程误差可以通过尽量使镜间距离为0消除。因此,环境因素对误差测量影响最大。
为验证环境因素对误差测量的影响程度,在标准环境和参数修正后实际环境状态下分别对轴、轴的定位误差进行测量。测量时标准环境与实际环境参数如表3所示,测量结果如图3和图4所示。

图3 X轴定位误差对比 图4 Y轴定位误差对比
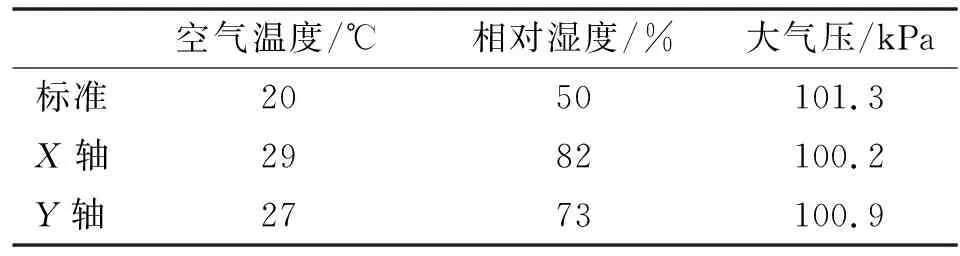
表3 环境参数
在试验过程中,由于两种环境下测量时间相隔较短,从而忽略温度变化和被测件线膨胀对铣床造成的误差。依据Edlen经验公式,由环境因素变化造成的测量误差可用式(4)表示:
=-0926×10-0039×10+
0258×10
(4)
式中:、和分别为空气温度、空气湿度和大气压力相对于标准状态的变化量。
根据式(4)可以计算出轴、轴由环境参数变化引起的理论测量误差、分别为-7.9、-5.8 μm;而通过激光干涉仪直接测量的实际误差测、测分别为-8.7、-5.1 μm,与理论计算值比较吻合,说明参数修正后铣床定位更加准确。
2.2 三因素双指标正交试验
为获得最优方案,分析MIMO系统时通常采用正交试验法。正交试验设计法将输入量称为因素,输出量称为试验指标;所需的试验次数最少且选出的数据点均具备均匀分散、齐整可比的特点,是一种高效、可靠、引出结论价值度高的试验设计方法。试验结果主要由极差分析法分析,如式(5)所示:

(5)
式中:为极差,指第列各个水平下试验结果平均值的最大、最小值之差;为第列因素水平所对应的试验结果和。依据的大小,就可以判断该因素对试验结果的影响程度。本文作者将此方法应用到数控铣床的三因素双指标正交试验中。
通过大量试验研究得出在利用激光干涉仪进行误差测量时,数控铣床加工时的进给速度、时间以及测距对测量结果影响极大。因此,在三因素双指标正交试验中,将进给速度、时间以及测距作为输入变量因素,把螺距累积误差与反向间隙作为输出即试验指标,通过仅改变三因素中一个因素的方法测量MVC850B数控铣床的定位误差,通过统计测量结果,得到两个试验指标极差值如表4所示。

表4 正交试验响应结果极差值 单位:μm
由表4可知:三因素中,相比铣床加工时间,其他两因素对反向间隙的影响权重更大;相反,与其他两因素相比,铣床加工时间对螺距累积误差的影响权重明显更大。
2.3 单因素对比试验
虽然三因素双指标正交试验可以判断3个因素对反向间隙与螺距累积误差影响的主次关系,但不能反映出试验输出结果在某个单因素影响下的变化情况。因此,进行单因素对比试验,定量分析三因素中单个因素对反向间隙与螺距累积误差的影响,结果如图5—图8所示。
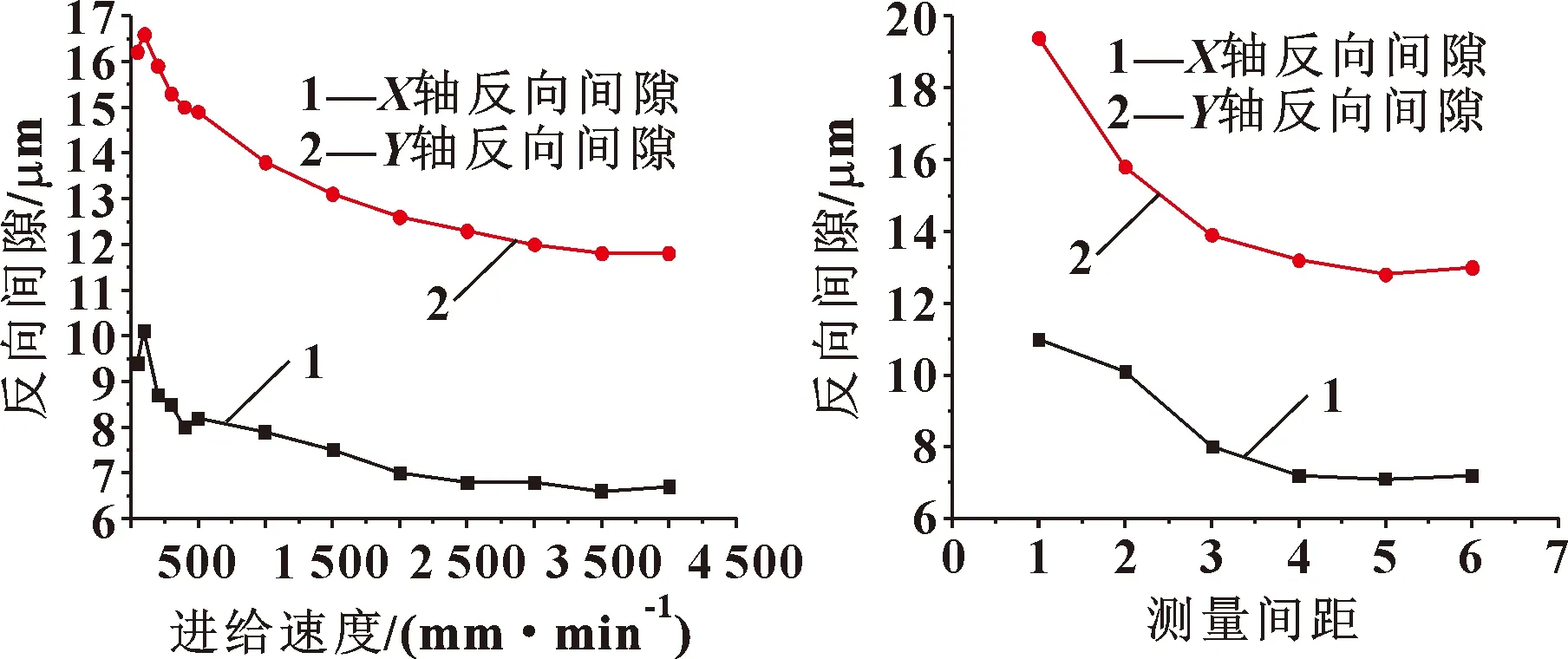
图5 反向间隙随进给速度的变化 图6 反向间隙随测量间距的变化

图7 X轴螺距累积误差随加工时间的变化

图8 Y轴螺距累积误差随加工时间的变化
分析进给速度对反向间隙的影响时,测量间距取50 mm保持不变。由图5可知,两轴反向间隙总体随进给速度的增大呈下降趋势,进给速度大于2 500 mm/min后,反向间隙基本保持不变。
分析测量间距对反向间隙的影响时,取进给速度为2 500 mm/min,为了方便观察及作图,横轴的1~7点分别代表测量间距为1、5、10、20、50、100、150 mm。由图6可知,随着测量间距的增加,两轴反向间隙逐渐减小,当测距达到20 mm时,反向间隙基本保持平稳。
分析两轴对螺距累积误差的影响时,取测量间距为50 mm、进给速度为2 500 mm/min。铣床从1 h运转至13 h,取得定位误差。由图7和图8可知:轴、轴的螺距累积误差的绝对值随着加工时间的增加而变大,而且1~13 h的变化趋势基本一致。这是因为铣床传动部件的线性膨胀系数一般较为固定,铣床温度随着加工时间的持续增加而不断升高,在单位时间内温度变化较均匀,导致铣床螺距误差变化较为一致。因此,当数控铣床加工工件时,不仅需要及时给机床散热而且需选择合适的进给速度和加工路线。
3 数控铣床定位误差补偿
3.1 定位误差补偿策略
根据前面分析可知,反向间隙会影响螺距累积误差和重复定位精度,因此在补偿时采用先进行反向间隙补偿,后采用基于坐标系偏移的方式对数控铣床定位误差进行半闭环前馈补偿的方式来补偿定位误差。
3.2 反向间隙补偿
反向间隙广泛存在于数控铣床传动链的各环节中,当铣床工作台在其运动方向上换向时,由于反向间隙的存在会产生失动现象。因为铣床各位置丝杆磨损和装配不同导致轴上各位置点的反向间隙值也会不同,所以需将丝杆按等间隙值分成几段。
刀具在平面内的理想运动路径为从点到点的粗实线,如图9所示。假设只在轴运动方向上发生改变,而保持轴不变。设为轴方向上点的坐标位置,则为点反向间隙值。因受反向间隙的影响,加工过程中实际路径为→→→′→′→′→′4→。如使反向间隙补偿后刀具沿着→→2→3→4→→运动,就可实现→→→→→理想运动路径。依据图9,当运动直线在方向上的斜率为正时,反向间隙为0;如果斜率为负,则反向间隙为,此时应进行反向间隙误差修正。

图9 反向间隙的补偿路径
误差测量和补偿必须在同一基准点进行。在反向间隙补偿试验中,应首先执行反向超程操作,以消除第一次反向间隙对首次进给运动的影响,然后以100 mm为间距,选取铣床零点作为基准点对数控铣床反向间隙进行测量与补偿。测量与补偿的流程如图10所示。

图10 反向间隙误差测量补偿流程
根据测得的反向间隙值在数控铣床参数设置中输入1851命令进行补偿,得到轴、轴反向间隙补偿前后效果对比如图11、图12所示。

图11 X轴反向间隙补偿前后对比 图12 Y轴反向间隙补偿前后对比
由图11、图12可知:通过反向间隙误差补偿,可使得反向间隙大大减小、定位精度大大提高。
3.3 铣床定位误差补偿
每次开机,铣床都需要返回零点,定位误差除了存在于工件加工范围内,还存在于加工坐标系与铣床坐标系之间。如果两坐标系原点之间的相对距离可以实时更改,使程序指令在新的坐标系运行,就可以精确补偿定位误差。这便是基于坐标系偏移功能的误差补偿原理,如图13所示。

图13 基于坐标系偏移功能的误差补偿原理
原坐标系中工件某定位点的理论位置用表示,实际点用′表示,假设(、、)为和′两点之间的误差。在实际加工时,原点将沿、、轴分别平移、、,得到实际的加工坐标系′-′′′。点用坐标系偏移误差补偿后,将其校正为坐标系′-′′′中的″,而″的坐标仍为(,,)保持不变,该方法可以在数控铣床加工之前实现误差补偿。
3.4 验证试验
为尽可能全面地验证定位误差补偿效果,并结合MVC850B三轴数控铣床的加工特点,验证试验采用试切法,设计出如图14所示的工件加工图;通过比较加工后的工件精度,验证补偿效果。为降低切削力引起的误差,试验工件的材料为铝块。准备2块尺寸为200 mm×200 mm×20 mm的加工工件毛坯,工件1用于未补偿加工试验,工件2用于定位误差补偿后的加工试验。通过4个定位点可以反映出补偿后数控铣床和轴方向上定点运动效果和定位精度;通过测量2条对角线直线度可以反映两轴联动以及直线运动补偿效果;通过测量4条边线各自的直线度可以验证两个轴正反行程位置精度以及直线运动补偿效果。

图14 试切法的零件加工图
此次试验采用10 mm的直柄键槽铣刀,主轴转速为500 r/min,取500 mm/min的加工进给速度加工工件。首先加工4个定位孔(按照I~IV点的顺序),然后再加工1、2两条对角线,最后进行3、4、5、6四条边的加工。得到的未补偿加工工件1如图15(a)所示。
首先,使用数控铣床1851指令补偿反向间隙,并且必须事先将螺距误差补偿值清零,以防止螺距误差补偿和程序补偿重叠增加新的误差。同时,应尽量使两次加工条件一致,减少环境等其他外界因素的影响。然后,使用基于坐标系偏移功能来补偿数控铣床的定位误差。补偿后得到的工件2如图15(b)所示。

图15 2个工件对比
为对比对MVC850B数控铣床的补偿效果,采用美国某公司生产的GLOBAL STATUS575型号的三坐标测量机(以下简称CMM)进行定位点的位置测量以及直线的直线度测量,测量机主要性能参数如表5所示。CMM是一种基于坐标测量的新型高效精密测量仪器,采用的柔性悬挂系统和空气轴承能提高长期稳定性和测量精度;采用伺服电机驱动和高分辨率的光栅使其具有超强抗干扰能力和抗磨损功能;采用经过硬处理的全铝框架,刚性强、质量轻、导热性好;工作台采用质量较大的花岗岩,减少振动并为活动桥的运动提供支撑。

表5 CMM主要性能参数
将图15中的两个工件分别放在CMM花岗岩工作台上进行测量,如图16所示。

图16 加工工件的精度测量
应用CMM自带的测量软件,采用基于特征测量的方法进行数据处理,得到测量结果如表6所示。
从表6可以明显看出:经过数控铣床定位误差补偿后,定点运动、双轴联动效果和正反行程位置精度较补偿前均有很大程度提高。通过大量试验对比和轴重复定位误差以及占总误差的占比得到,相比轴,轴的磨损更加严重,故对轴补偿前后精度进行对比测量,结果如表7所示。可以看出:补偿后轴定位精度大大提高,其中双向定位精度由82.351 μm提高到12.372 μm,提高了84.97%;反向差值由5.236 μm减小到3.127 μm,减小了40.27%。最终通过比较知补偿前、补偿后加工工件的尺寸精度提高了62.5%。

表6 2组工件参数对比 单位:mm
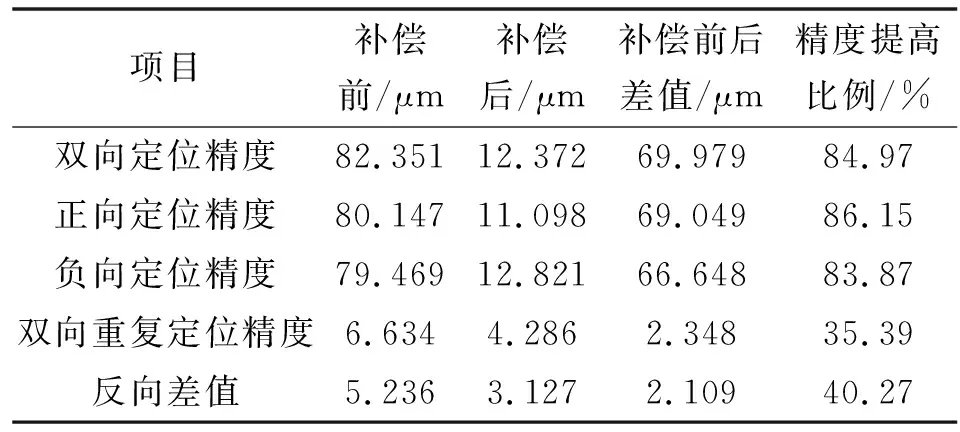
表7 Y轴补偿前后精度对比
综上所述,基于坐标系偏移功能的误差补偿方法可以有效提高工件加工精度,补偿后加工工件的尺寸精度提高了62.5%。该方法可作为定位误差补偿的有效途径之一。
4 结论
(1)铣床定位误差测量受空气温度、空气湿度和大气压力等环境因素影响,其中受空气温度影响远大于其他两个因素,空气湿度对其影响最小可忽略不计。
(2)反向间隙受进给速度和测量间距影响较大,它随着进给速度和测量间距的增大而减小;而螺距累计误差受加工时间影响更大,它随着加工时间的增加而逐渐增大。
(3)数控铣床定位误差补偿试验结果表明,所提出的误差补偿策略可以有效提高工件加工精度,补偿后加工工件的尺寸精度提高了62.5%,可以作为定位误差补偿的有效途径。
