基于整槽偏移对齿槽转矩和铁心损耗的研究

张海，彭武,姜琦

(华东交通大学,载运工具与装备教育部重点实验室，江西南昌 330013)

0 前言

轮毂电机作为电动汽车驱动系统的核心部件之一，其齿槽转矩与铁心损耗会影响电机的性能。永磁电机的齿槽转矩是电枢铁心的齿槽与转子永磁体相互作用而产生的磁阻转矩。齿槽转矩的产生会导致电机的振动和噪声，尤其在轻载和低速情况下表现尤为明显。而铁心损耗过大，会使电机内部温升增加，直接影响电机的运行效率。故本文作者以永磁无刷直流轮毂电机为研究对象，提出一种能够降低齿槽转矩和铁心损耗的方法。

国内外已有专家对抑制齿槽转矩进行了研究。ZHU和HOWE研究了不同设计参数对永磁电机齿槽转矩的影响，但缺少仿真验证或实验验证。ZHU等利用能量法和傅里叶级数分析，推导出齿槽转矩的一般解析表达式。YANG等将改进的区域消去法、有限元法和解析法相结合，对永磁电机的极弧系数进行优化，使永磁电机的齿槽转矩最小。ISLAM等研究了永磁同步电动机的槽极组合和磁体形状对转矩波形幅值和谐波含量的影响。DUTTA等研究了分段式内永磁电机的齿槽转矩减小问题，但缺少实验验证。ZHU等对永磁无刷电机齿槽转矩的叠加计算方法进行了评价，但未对低次谐波进行分析。LATEB等提出了一种减小永磁电机齿槽转矩的方法，但未对优化结果进行定量计算。LUKANISZYN等提出了一种用离散斜交角的表面贴装磁铁来减小永磁电机齿槽转矩的方法，但缺少理论公式推导。KIM等提出一种考虑极弧比和凸极参数的永磁电机转子设计方法来降低齿槽转矩，但缺少实验验证。JIANG等在有限元分析软件flux2D中建立并计算了表示不同槽极特性的模型，但缺乏实验数据支持。杜晓彬等利用傅里叶分解对齿槽转矩进行分析，但并未进行实验分析。杨玉波等提出了磁极偏移角度对原有齿槽转矩谐波以及新引入的低次谐波都有较好的削弱作用，能较好地减小齿槽转矩。杨玉波等通过改变相邻两槽的槽口宽度来减小齿槽转矩，并利用有限元法进行了验证。王晓远和贾旭利用响应曲面法研究槽口偏移角度和槽口宽2个因素之间的数学模型，并得出最优解组合，但未考虑低次谐波的影响。

国内外研究轮毂电机铁心损耗的学者较少。张辉等人通过JMAG-Express参数化模块，证明电机铁心的材料及其厚度影响电机的铁损，但缺少实验验证。MATERU和KRISHNAN推导了铁心不同部位磁通频率的一般表达式，采用傅里叶分析方法将磁通波形分解为其组成的正弦分量，再结合铁心材料的损耗特性来估计相应的损耗分量。HAYASHI和MILLER提出了一种计算铁心损耗时考虑磁通波形的新方法，并给出了磁路各部分磁通之间的矩阵方程关系，但未进行仿真实验。宋泽等人提出一种基于正交分解和损耗分离的改进无取向硅钢叠片旋转铁心损耗模型，其计算精度得到较大提高。RAULIN等将铁心损耗模型分为涡流损耗和磁滞损耗两部分，并将损耗作为磁通密度导数的函数进行建模，并预测了铁心损耗随时间的变化，但缺少实验验证。

基于以上文献中的分析结果，本文作者提出一种基于整槽偏移的方法来削弱齿槽转矩和铁心损耗。建立轮毂电机的物理模型，在原模型的基础上分别给出各个偏角的物理模型，并在Maxwell软件中进行仿真，分析得到的齿槽转矩和铁心损耗结果，验证模型的正确性。

1 齿槽转矩分析

对于永磁电机，齿槽转矩的解析表达式为

(1)

式中：为槽数；2为极数；为铁心长度；对于外转子结构，和分别为定子外半径和转子轭内半径；对于内转子结构，和分别为转子轭外半径和定子内半径；为使2为整数的整数。

文中所使用的模型为某型电动汽车轮毂电机，为永磁无刷直流电机，轮毂电机各参数如表1所示。根据表1,可在AutoCAD软件中画出轮毂电机二维CAD模型如图1所示。因为本文作者研究的是整槽偏移对轮毂电机性能的影响，所以在AutoCAD软件中对原始模型进行修改，对整槽进行偏角处理，偏角范围为0～8°，并将处理好的CAD模型导入Maxwell软件中;对9个模型添加材料、激励和边界条件等等，Maxwell偏角模型如图2所示。

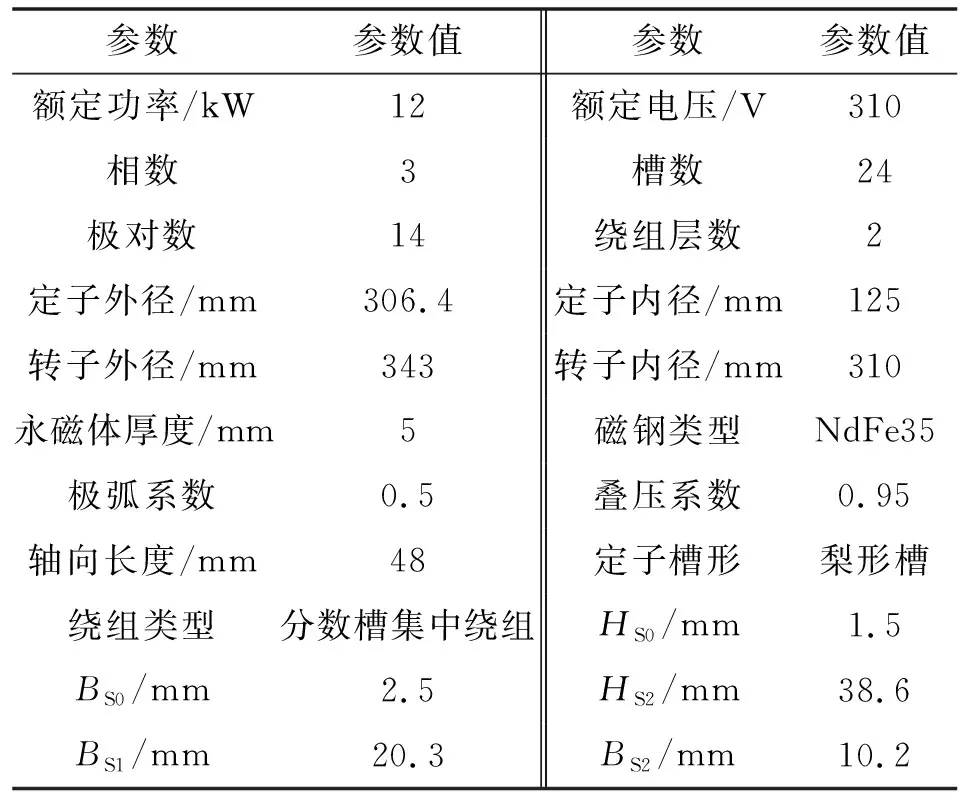
表1 轮毂电机具体参数

图1 轮毂电机二维CAD模型

图2 Maxwell偏角模型

对图2中的偏角模型进行有限元仿真，可得出各个偏角模型的齿槽转矩波形。图3所示为各个偏角齿槽转矩的汇总，由于中间曲线分布过密，为方便观看，将中间部分放大，如图4所示。图5所示为各个偏角时的齿槽转矩最大值。

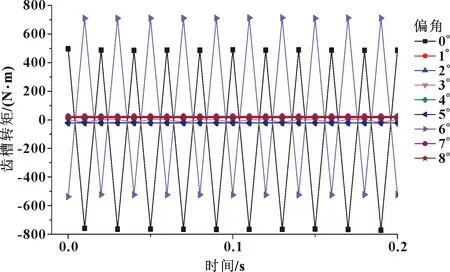
图3 齿槽转矩汇总

图4 齿槽转矩汇总曲线中间部分放大图

图5 齿槽转矩最大值

由图3—图5可知:随着整槽偏角增大，齿槽转矩先减小后增加再减小;0°偏角的原始模型的齿槽转矩最大，0°以后齿槽转矩有显著降低;1°～5°之间的走势是个平缓的折线，齿槽转矩并没有明显的增大或减小，而当偏角为6°时，齿槽转矩突然增大，又达到一个高峰，但数值低于偏角为0°时的齿槽转矩;在6°以后，其齿槽转矩明显降低;在偏角为8°时，齿槽转矩达到最小，最小值为14.664 4 N·m。通过上述分析可知，通过整槽偏移角,可明显降低齿槽转矩，但其削弱作用没有明显的规律性，随着偏角度数的增大，其削弱作用时而大时而小。

2 铁心损耗分析

产生铁心损耗的原因比较复杂，永磁电机铁耗受到很多因素的影响，如永磁电机磁场频率、硅钢片材料特性和加工制造工艺等。目前，应用最广的铁耗分析模型是BERTOTTI等提出的铁心损耗分离模型，其具体表示如下：

=++

(2)

式中：为永磁电机铁心损耗；为永磁电机磁滞损耗；为永磁电机经典涡流损耗；为永磁电机附加损耗。

对图2所示的偏角模型进行有限元仿真，可得出各个偏角模型的铁心损耗曲线如图6所示。由于下部曲线分布过密，为方便观看，将下部分曲线放大，如图7所示。铁心损耗最大值如图8所示。

图6 铁心损耗汇总

图7 铁心损耗汇总曲线下部分放大图

图8 铁心损耗最大值

由图6—图8可知:随着整槽偏角的增大，铁心损耗先减小后增加再减小;0°偏角的原始模型的铁心损耗最大，0°以后铁心损耗有显著降低;1°～5°之间的走势是个平缓的折线，铁心损耗并没有明显的增大或减小;当偏角为6°时，铁心损耗突然增大，又达到一个峰值，但数值低于偏角为0°时的铁心损耗；在6°以后，铁心损耗明显降低；在偏角为4°时，铁心损耗最小，为79.090 6 W。通过上述分析可知，整槽偏移对降低铁心损耗有明显作用，但其削弱作用没有明显的规律性，随着偏角的增大，其削弱作用时而大时而小。

3 模型的有限元验证

通过对比图5和图8，可以发现齿槽转矩最大值和铁心损耗最大值的走势一致，且齿槽转矩和铁心损耗的最小值都出现在整槽偏角为3°附近，因此以偏角为3°时的轮毂电机模型作为验证模型。图9所示为轮毂电机整槽偏角为3°时不同时刻的磁力线分布。

图9 轮毂电机整槽偏角为3°时不同时刻的磁力线分布

由图9可知：随着外转子位置和时间的变化，轮毂电机的磁力线沿周向变化；从局部看，外转子磁力线从永磁体的一端连接到另一端，磁力线之间的距离是均匀的；每个永磁体是磁力线的起点和终点；内定子磁力线的密度不均匀，这与定子内部的磁场强度有关；在内部定子的槽中，几乎没有磁力线通过。无论是0、0.1、0.2 s还是0.3 s时刻，轮毂电机的内部均未出现较严重的漏磁情况，基本符合轮毂电机磁力线的分布情况。

图10所示为轮毂电机整槽偏角为3°时，不同时刻的磁密分布。可知：磁通密度的最大值约为2.38 T，该值出现在气隙附近的部分内定子齿端部；外转子与永磁体侧向间隙之间的磁通密度分布较均匀，其中外转子的磁通密度在径向方向，离气隙越远，磁通密度越小；气隙的磁通密度幅值略低于永磁体中的磁通密度幅值，分布也较为均匀；内定子的磁通密度主要集中在内定子槽内，部分槽与槽之间的磁通密度分布是均匀变化的；随着外转子所处的时刻、角度的不同，磁通密度云的分布在圆周方向上发生了变化，但在径向上基本保持不变。

图10 轮毂电机整槽偏角为3°时不同时刻的磁通密度分布

轮毂电机中的定子绕组形成了闭合电路，电流激励为0，此时只有永磁体励磁作用，线圈绕组在外转子上的永磁体的作用下会产生相应的旋转磁场，形成一定的感应电动势。图11所示为轮毂电机整槽偏角为3°时的感应电动势曲线，可知：轮毂电机的感应电动势波形呈正弦函数分布；绕组3相比绕组1、2更快地进入空载稳定状态；其感应电动势的最大幅值约为225 V，相比于轮毂电机的额定电压幅值310 V，其比值在合理的取值范围内，说明轮毂电机设计合理。

图11 轮毂电机整槽偏角为3°时的感应电动势波形曲线(瞬态场)

由图12可知，绕组磁链周期约150 ms，最大幅值约为2.25 Wb，并且呈正弦周期性变化;与感应电动势波形曲线不同的是，绕组1最先达到空载稳定状态。

图12 轮毂电机整槽偏角为3°时的绕组磁链曲线(瞬态场)

4 谐波分析

由前文的模型有限元验证可知，在偏角为3°时，其模型满足设计要求，故采用偏角为3°时的模型,利用傅里叶分解得到各次谐波幅值分布，并与未偏角时的模型的谐波幅值分布进行对比,结果如图13所示。可知:整槽偏移3°后，齿槽转矩中一次谐波被显著削弱,且其他低次数的谐波幅值没有明显增长。可见，采用所提整槽偏移方法在降低齿槽转矩一次谐波的同时,没有引进新的低次谐波。

图13 谐波对比

5 结论

本文作者采用整槽偏移的方法对电动汽车轮毂电机的齿槽转矩和铁心损耗进行定量分析，分别对0°～8°偏角时的轮毂电机模型进行有限元分析并得出相应的结论。通过分析，选定以整槽偏移角为3°时的轮毂电机模型为对象进行分析，结果表明：其齿槽转矩和铁心损耗均可取到最优值，且齿槽转矩降低幅度约为98%、铁心损耗降低幅度约为65%、一次谐波降低幅度约为96%。