基于MTMD的大跨人行悬索桥减振措施研究

张彦玲， 程 艺， 王泽涵， 王昂洋

(1.石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室，河北 石家庄 050043;2.石家庄铁道大学 土木工程学院，河北 石家庄 050043；3.国网河北省电力有限公司 沧州市供电分公司，河北 沧州 061000)

0 引言

由于新材料的使用和更现代化的施工和设计方法，以及充分考虑建筑与环境的融合，人行桥向轻质、细柔方向逐步发展，这也导致桥梁自振频率较低，可能会引起行人的舒适性下降，甚至发生人桥共振现象危及人身安全，当舒适度不满足要求时则需采用必要的减振措施。

减振方法主要分为2种：一种是通过改变桥梁结构自重与刚度从而达到降低振动响应的效果；另一种是利用调谐质量阻尼器(TMD)进行减振。Den[1]提出了TMD概念，分析了无阻尼吸振器的理论，并对不同参数的单个TMD系统减振效果进行分析，得到了最优的控制参数求解方法，并总结了最优的参数表达式；基于TMD，王立彬等[2]对某大跨钢结构人行桥、刘梦渝[3]对人行拱桥和人行悬索桥进行了减振分析。1984年，Iwanami et al[4]提出了由多个TMD组成的STMD系统的概念，但其减振效果依赖于自身频率与主结构频率精确接近，导致其自身控制的有效频率范围受限。1987年，Clark et al[5]设计出了多重调谐质量阻尼器装置(简称MTMD)，其设计原理与TMD一致，主要不同在于MTMD选取多个STMD子结构控制多种频率，从而改进了TMD系统的控制稳定性和控制带宽较小的问题。肖学双[6]、Li et al[7]分别采用MTMD对钢结构人行桥进行舒适度及振动控制研究，提出了此类人行桥的舒适度评价标准；高飞[8]针对小半径曲线梁桥的弯扭耦合受力特性，研究了TMD和MTMD对其在地震作用下震动的控制效果；Domizio et al[9]研究了地震作用下结构的非线性动力响应，进行了MTMD减振系统的参数优化。

针对不同桥梁的独特性，MTMD的设置效果也不相同。以某带风缆的大跨径人行玻璃悬索桥为工程背景，采用Midas建立有限元模型，首先进行自振特性和主梁的人致振动分析，并对行人舒适度进行评价，然后基于多重调谐质量阻尼器装置MTMD对主梁进行竖向减振措施研究，通过MTMD系统的参数选取和优化，得到最佳减振效果，验证MTMD在大跨径人行玻璃悬索桥上的减振效果。

1 工程背景

某地锚式单跨简支玻璃人行悬索桥，桥面宽度4.6 m，主缆跨径布置为(40+580+40)m，矢跨比为1/10.8，矢高53.3 m。主缆采用19股91丝Φ5.1 mm的镀锌高强度平行钢丝成品索；吊杆沿顺桥向布置，间距为3 m，采用61丝Φ5 mm的平行钢丝成品索。抗风缆跨度516 m，面内矢跨比为1/17.2，采用3股91丝Φ5.1 mm的镀锌高强度平行钢丝成品索；抗风拉索采用Φ30 mm的ZAA6-7+WSC1 770钢丝绳，平行布置，自距离索鞍38 m起，每隔6 m布置一根抗风拉索。抗风拉索所在平面与主梁水平面夹角为30°。采用无塔式结构，将塔索鞍设立在山头上。主梁标准节骨架由纵梁和横梁构成，纵、横梁皆为箱型截面，钢材采用Q345。标准节高为0.6 m，宽为3 m。桥面板采用特制钢化玻璃安装在2个纵梁之间。桥梁布置如图1所示。

图1 人行悬索桥布置图(单位：m)

2 人致振动及行人舒适度分析

2.1 有限元模型

采用Midas/Civil建立有限元模型，其中主缆、吊杆、抗风缆和抗风拉索采用索单元，主梁和横梁采用梁单元。边界条件为：① 主缆锚碇处、抗风缆锚碇和索鞍底部处做固结处理；② 主缆在索鞍处释放X轴(纵桥向)方向的位移约束；③ 主梁一端为固定铰支座，另一端为活动铰支座；④ 主缆和吊杆、吊杆和主梁、抗风拉索和主梁、抗风缆和抗风拉索之间均采用刚接。由于悬索桥属于柔性结构体系，表现为非线性大变形，因此进行了合理成桥状态的主缆和抗风揽精确线形。找形后得到的有限元模型共1 912个节点，2 760个单元，其中梁单元1 729个，索单元1 031个。全桥模型及主梁局部模型如图2所示。

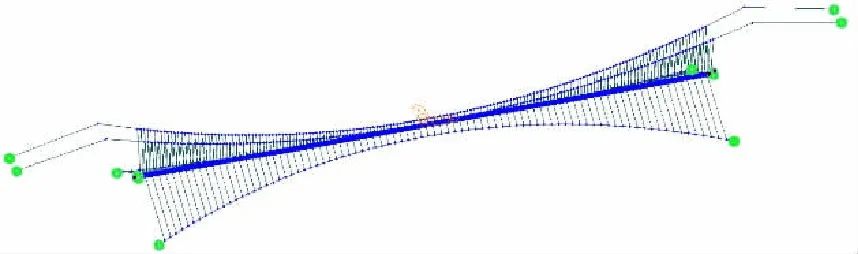
图2 有限元模型图

2.2 人致振动分析

2.2.1 行人荷载

行人荷载依据文献[10]选取，计算公式为

P(t)=P0cos(2πfpt)n′ψ

(1)

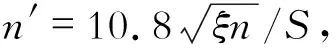
2.2.2 行人步频范围内的振型及频率

依据文献[10]规定，行人竖向一阶频率在1.25～2.3 Hz之间；横向一阶频率在0.5～1.2 Hz。当行人荷载频率与桥梁频率一致时易引起共振，因此需选择行人步频范围内的振型进行舒适度研究。通过特征值分析，可以得到不考虑人群密度，以及取行人密度n分别为0.5、1.0、1.5、2.0人/m2时，行人步频范围内的横弯及竖弯自振频率，以及行人频率取该频率时的折减系数ψ，见表1所示。

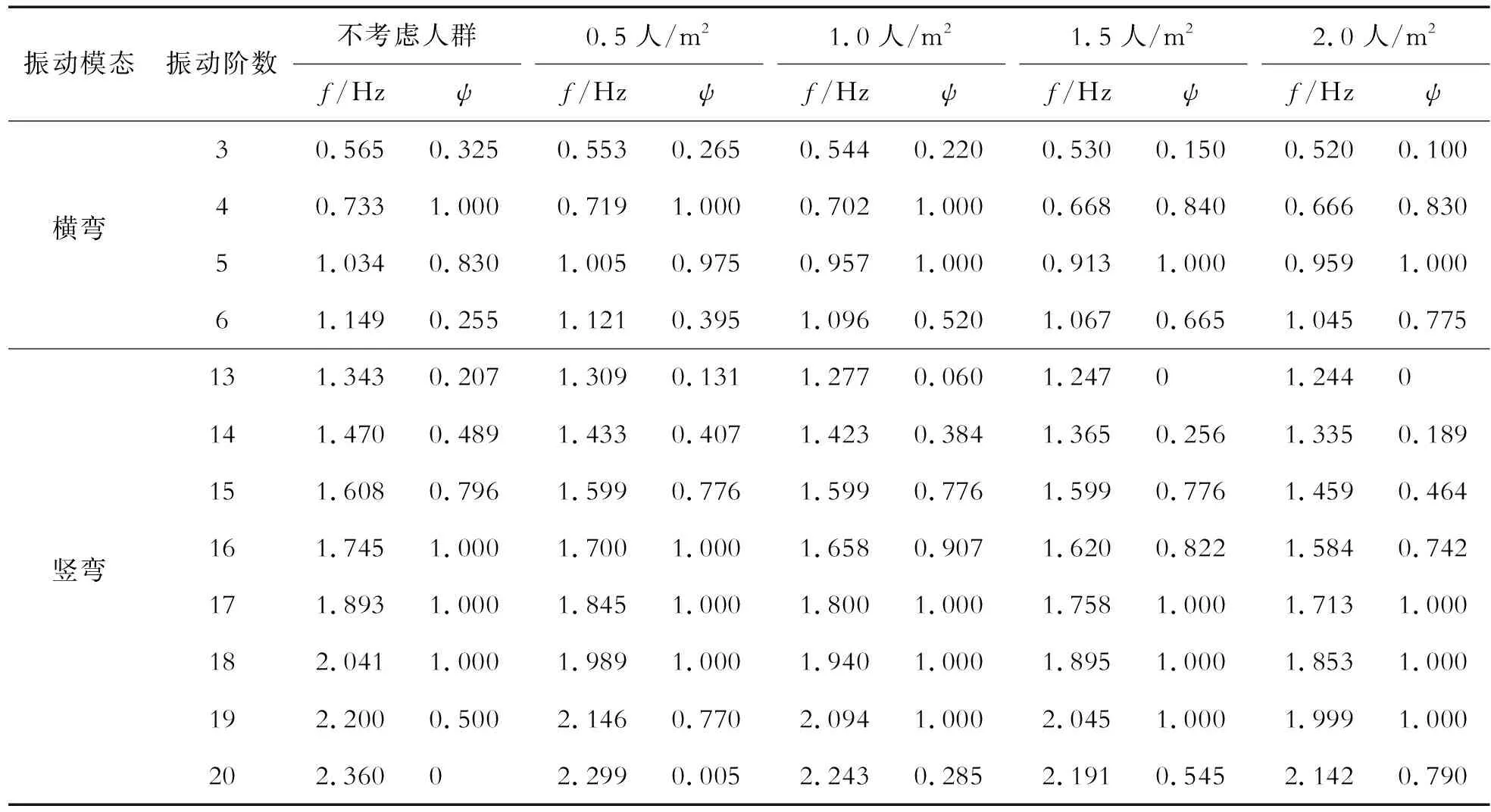
表1 竖向和横向步频范围内的自振频率及折减系数ψ

2.2.3 人致振动响应

根据式(1)所示的行人谐波荷载模型，取fp为表1中各阶模态所对应的频率，行人密度n分别取0.5、1.0、1.5、2.0人/m2，并根据图3计算横向及竖向振动折减系数ψ值，得出不同频率下的行人谐波荷载，然后根据相应的主梁振型图按最不利方式施加到主梁节点上，计算各谐波荷载下主梁各节点的加速度时程，并识别出加速度时程中的最大加速度值，再通过比较取出各节点中最大加速度值的极大值，简称为加速度极大值。重复以上计算过程，求得不同行人密度下主梁的加速度极大值，见图3和图4。

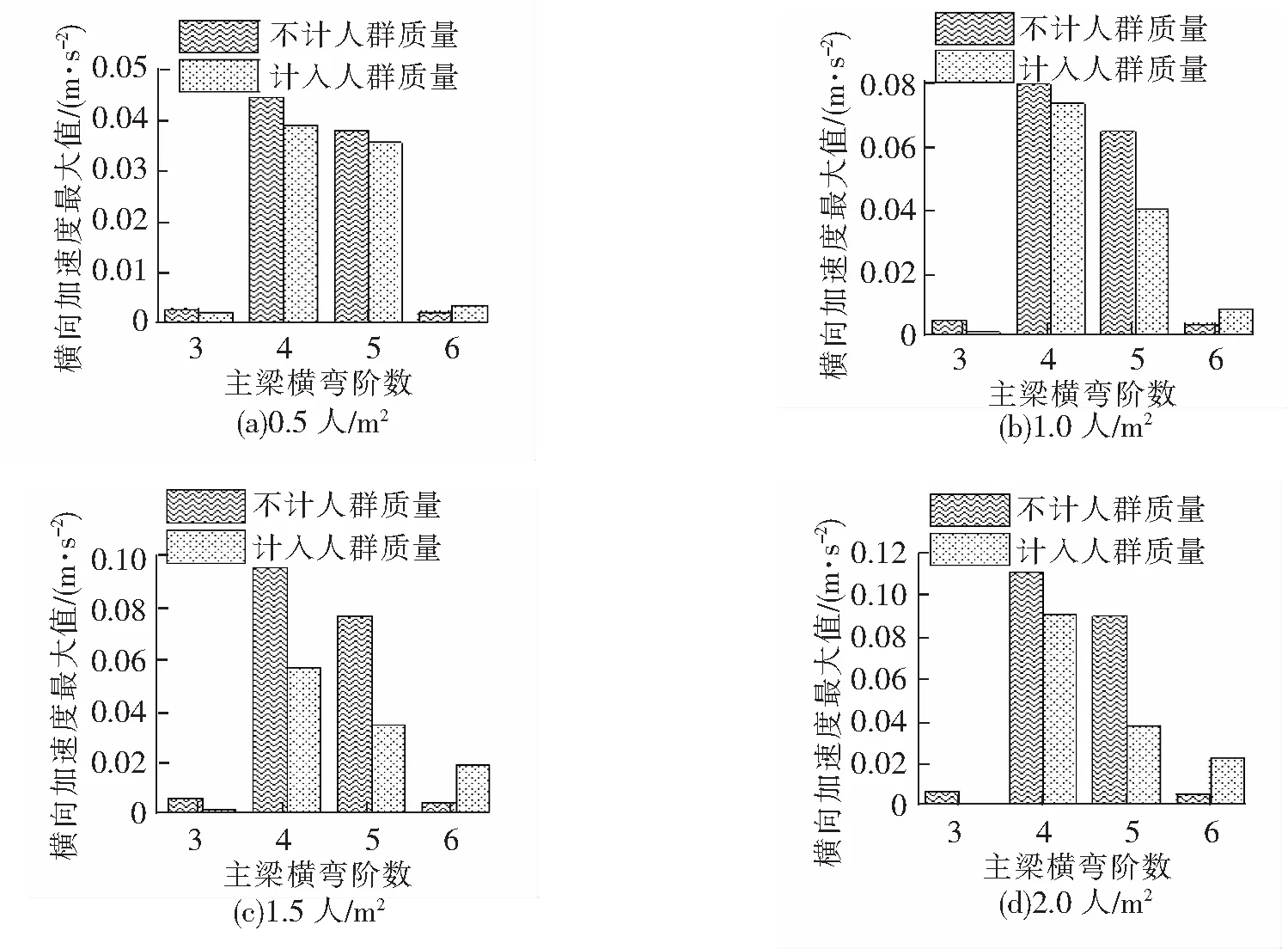
图3 不同行人密度下主梁横向加速度最大值

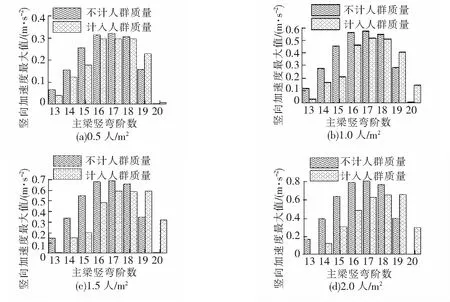
图4 不同行人密度下主梁竖向加速度最大值

由图3和图4可知，主梁横向和竖向加速度极值随行人密度的增加而增大；计入人群质量后，加速度极值下降；行人步频取桥梁不同阶固有频率时引起的主梁加速度极值不同，这与所加载的模态振型形状、不同步频时所对应的荷载折减系数ψ这2种因素有关。

2.3 行人舒适度分析

文献[10]根据结构加速度，将行人舒适度分为4个等级：加速度在横向小于0.1 m/s2、竖向小于0.5 m/s2时为很舒适状态；横向在0.1～0.3 m/s2、竖向在0.5～1.0 m/s2时为中等舒适状态；横向在0.3～0.8 m/s2、竖向在1.0～2.5 m/s2时为不舒适状态；横向大于0.8 m/s2、竖向大于2.5 m/s2时为不可忍受状态。

在图3和图4中，针对每一种行人密度，取出由不同步频下行人荷载所激励起的加速度最大值中的极值进行舒适度评价，如图5所示。

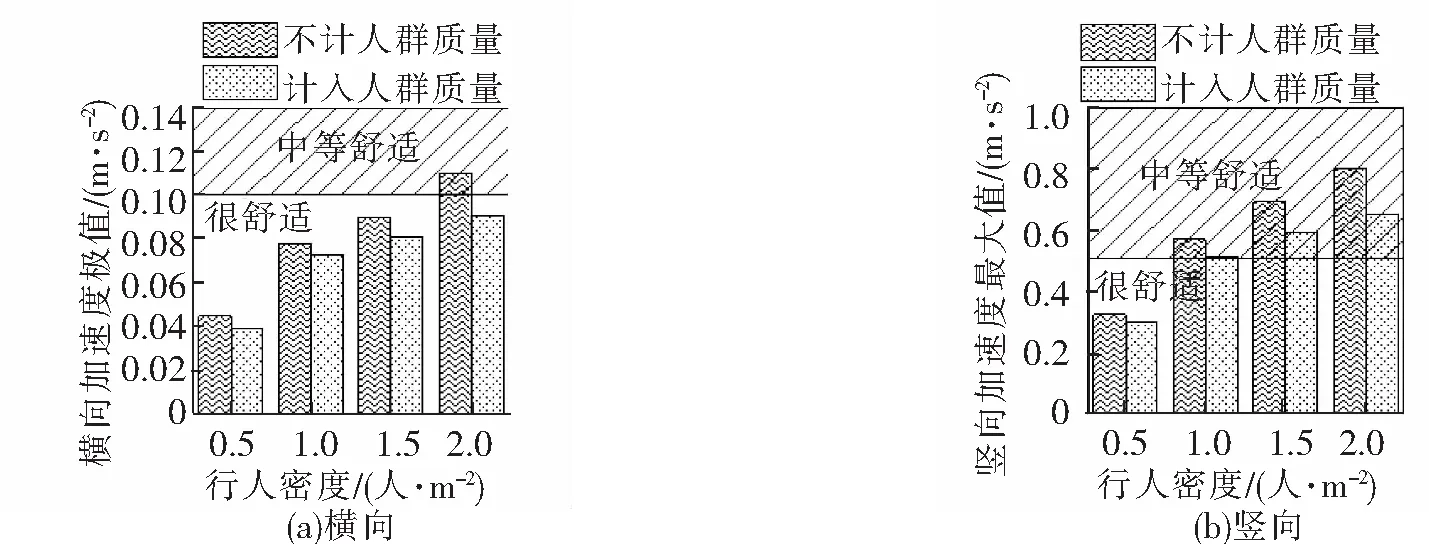
图5 竖直吊杆模型主梁加速度极值及舒适度评价

由图5可知，在行人密度区间[0.5人/m2, 2.0人/m2]内，该人行悬索桥在横向和竖向的人致振动均未进入不舒适区，但只有在行人密度为0.5人/m2下横向和竖向均处于很舒适区间，横向舒适度在行人密度为2.0人/m2时进入中等舒适区间，而竖向舒适度在行人密度为1.0人/m2时已进入中等舒适区。总体来说，该悬索桥的横向舒适度优于竖向舒适度，虽然竖向舒适度在行人密度为2.0人/m2时仍处于中等舒适区，但加速度极大值已达到0.8 m/s2，若在景区行人特别密集时仍可能进入不舒适区，因此需进行竖向减振分析。

3 基于MTMD的减振措施研究

3.1 调谐质量阻尼器系统减振原理

当主结构受到简谐荷载p(t)=p0sinωt时，安装TMD的无阻尼结构的动力响应放大系数可表示为[1]

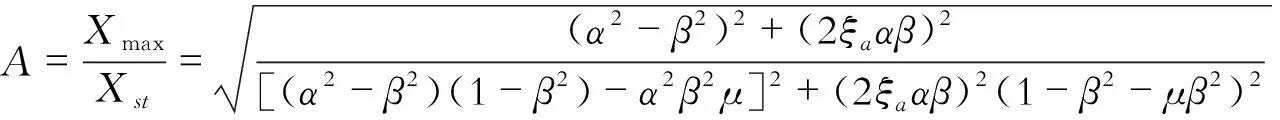
(2)

当ξα=0 (即TMD阻尼为零)及α=β(主结构和TMD频率相等)时，A≡0，则主结构达到了最优的控制效果。Den[1]给出了最优频率比αopt和最优阻尼比ξpot的具体计算公式

(3)

TMD的自振频率只有与主体结构的自振频率保持一致，才会表现出良好的减振效果，但实际运营过程中，桥梁结构在一定频率范围内会产生多种共振情况，因此单一的TMD系统并不能满足实际的减振需要，而MTMD系统由多个子结构TMD组成，每个TMD分别控制不同的振动频率，故可以控制多个模态的振动响应。MTMD系统需满足2个条件：①每个TMD控制相应的模态振动，即TMD自振频率与受控模态自振频率相同；②TMD分别放置在不同模态的振型位移最大处。主体结构施加MTMD后，在外界荷载激励p(t)作用下，设C为主结构阻尼，则桥梁结构的运动方程可表示为[11-12]

(4)

第i个TMD运动方程为

(5)

将MTMD和桥梁结构视作耦合运动系统，合并方程可得到整体的运动耦合方程

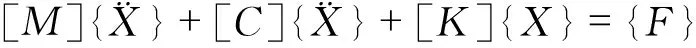
(6)

根据式(6)，结合Newmark-β法可以在时域内进行行人简谐波荷载作用下整体结构耦合系统的动力时程分析，也就是安装MTMD系统后桥梁结构的振动响应分析。

3.2 MTMD系统布置

由图5可知，在各种行人密度下，与行人步频产生共振并激起较大竖向加速度的振型主要包括第15、16、17、18阶竖向振动模态，故选取这4个竖向振动模态进行控制，针对每一阶振型设置一个子结构STMD，共4个。由于每个STMD系统质量较大，故分成4个频率相同的TMD阻尼器，如图6所示。

图6 MTMD系统结构图

STMD安装的位置根据4个频率下主梁的模态位移幅值来决定，从有限元模型提取出行人密度为2.0 人/m2时每个频率对应的振型最大位移正则化图，如图7所示。

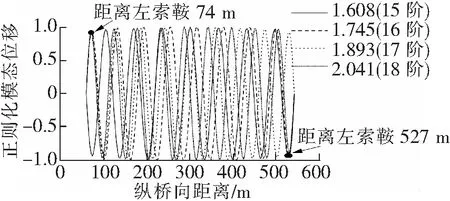
图7 不同频率下的竖向位移模态组合图

由图7可以看出，在纵向距离左索鞍74 m和527 m处，每个频率下主梁节点的竖向位移均产生了最大位移幅值，因此在这两处设置STMD子系统减振效果更明显。为了使结构受力更加对称，在每个位置附近设置2个子系统TMD，在74 m处设置TMD1系统和TMD4系统；在527 m处设置TMD2系统和TMD3系统，见图8。

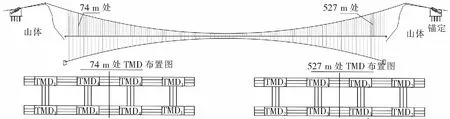
图8 MTMD系统安装布置图

3.3 MTMD初始参数确定

MTMD主要设计参数包括质量、刚度和阻尼。一般情况下质量和刚度对主结构的影响较大，应优先考虑。通常MTMD系统总质量为控制模态广义质量的1%～5%，此范围内MTMD成本低、效果好。基于第2节的人致振动分析，采用加速度为优化目标，按如下步骤确定MTMD参数：①选取MTMD与广义模态质量的比值μ；②依据式(2)并结合μ值，确定MTMD的最优频率比αopt和最优阻尼比ξopt；③确定对应于第n阶振动模态的子结构STMD的质量、刚度、阻尼，计算公式为[3]

(7)

式中，md为STMD的质量；Mn为第n阶受控模态的广义质量；ωs为受控模态频率；kd为子结构STMD最优刚度；cd为子结构STMD最优阻尼。

考虑到本桥跨度长，自重大等情况，MTMD系统与桥梁广义质量比μ取3%，故每个STMD系统初始质量按照桥梁广义质量的0.075%设置，则根据式(6)可得每个STMD系统的αopt=0.992 6，ξopt=0.052 8。再由式(7)计算出每个STMD系统的总刚度和总阻尼，如表2所示。由于桥梁频率受人群质量的影响，而MTMD的参数只能取固定数值，因此表2中的频率采用了不考虑行人质量时的数值。

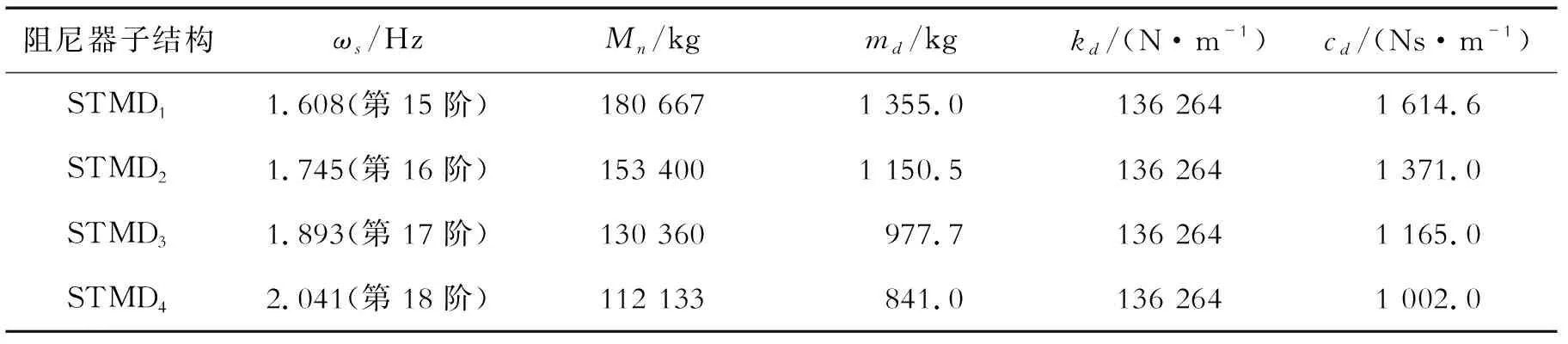
表2 MTMD的初始参数

3.4 MTMD参数优化

MTMD系统参数优化目的是使桥梁振动得到最优控制，同时MTMD系统参数达到最优。优化过程中应保持STMD自振频率与被控模态频率一致，故参数优化过程中，应使刚度参数与质量参数的变化比例相同；阻尼参数的选取主要与质量有关，因此阻尼参数变化应随着质量参数变化而变化。参数优化步骤如下。

(1)将表2中根据受控频率得到的每个STMDi(i=1,2,3,4)的质量mdi、刚度kdi和阻尼cdi的值定为基准值，取其比例系数η为1.0，然后变化比例系数η，使STMDi的各参数按比例变化。以控制第15阶竖向振动的STMD1为例，当η=0.5时，质量md1、刚度kd1和阻尼cd1的值分别为1 355×0.5=677.5 kg、13 624.4×0.5=68 132.2 N/m、1 614.6×0.5=807.3 Ns/m。通过类似的计算方式，计算出每个STMDi在各种比例系数下的结构参数mdi、kdi和cdi。

(2)把相同刚度系数下的每个STMDi中的4个TMD对应的mdi/4、kdi/4和cdi/4输入到被控振型中进行计算。例如，当比例系数为1.0时，将表2所列各STMDi的结构参数除以4，得到各子系统中每个TMD的参数，然后在Midas一般连接特性值中设置TMD参数，再使用一般连接建立TMD单元。根据不同的受控振型，按最不利方式在主梁上施加2.0人/m2的人群简谐波荷载，计算出比例系数为1.0时主梁各节点的竖向加速度，并取最大值，即主梁竖向加速度最大值。

(3)变化比例系数，重复以上计算步骤，可得到4个振动模态下主梁竖向加速度最大值随比例系数的变化，见图9(a)。定义减振率为加速度变化值与未施加TMD时主梁加速度最大值的比值，见图9(b)。

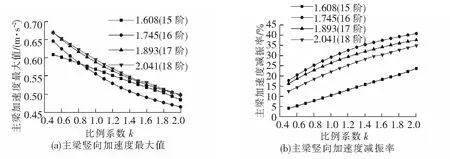
图9 主梁竖向加速度最大值及减振率随比例系数的变化

根据图9可以看出，随MTMD系统比例系数的增加，主梁竖向加速度最大值下降，减振率增加。其中，MTMD系统对第16阶竖向振动减振效果最明显，对第15阶减振效果最小。由图9(b)可见，比例系数越大，减振效果越好，但减振率并非随比例系数的增加而线性增加，而且过大的质量也会影响桥梁结构的正常使用，因此TMD的总质量与桥梁广义质量比μ的取值范围在1%～5%之间为宜。取比例系数k=1.8，在此工况下，4个STMD系统总质量在桥梁广义质量的5%左右；同时4个主控频率的主梁加速度均在0.5 m/s2附近，满足行人舒适度的要求。优化后MTMD系统中单个TMD的最终参数见表3。

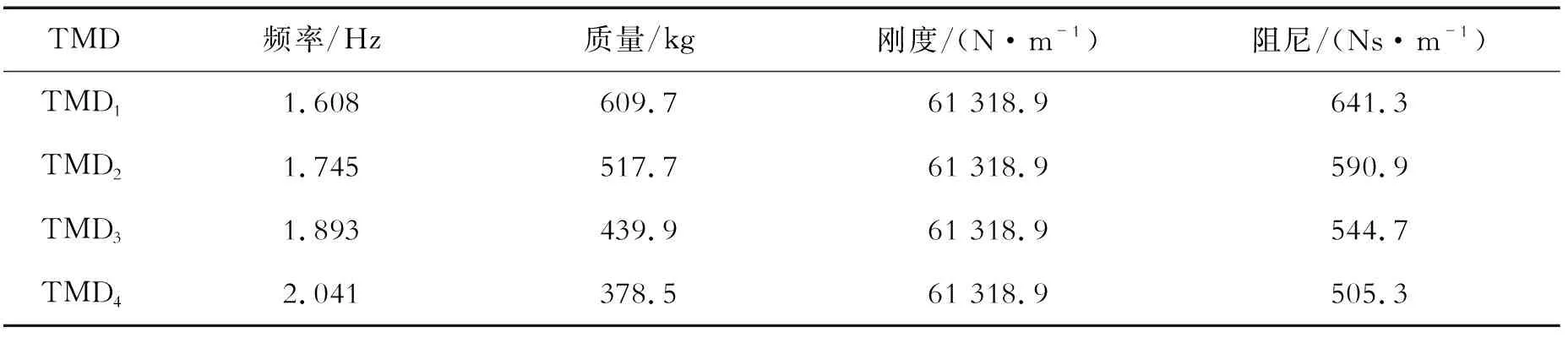
表3 MTMD系统中单个TMD最终优化参数

由于MTMD系统质量较大，需将这一部分荷载计入悬索桥二期荷载中重新进行建模找形，精确计算加入MTMD系统后的悬索桥受力情况。计入MTMD系统质量后，桥梁结构振型未发生变化；桥梁第15阶频率从1.608 Hz变化为1.607 Hz，其他频率变化也很小，因此该MTMD系统可以达到良好的减振效果。

4 MTMD系统减振效果分析

根据表3中的最优参数建立好MTMD系统后，根据不同的受控振型，按最不利方式在主梁上施加2.0 人/m2的人群简谐波荷载，得到在安装和未安装MTMD系统的条件下最大主梁节点竖向加速度，见图10。

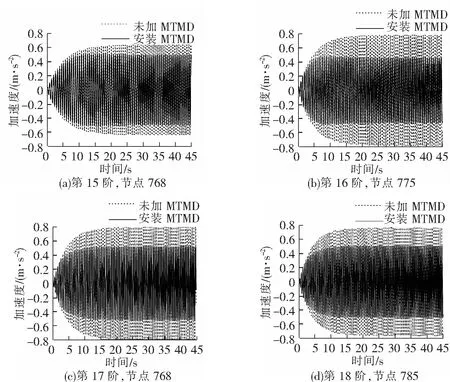
图10 有无MTMD系统时主梁最大竖向加速度时程比较图

从图10中可以看出，无MTMD系统时，主梁最大竖向加速度接近0.8 m/s2，已经接近不舒适的行走状态；当安装MTMD系统时，主梁节点最大加速度最大值在0.5 m/s2附近，已经达到舒适状态。由此可以看出，MTMD系统对主梁加速度最大值的减振效果明显。

对每个频率的全桥主梁节点加速度进行分析，得到主梁竖向加速度最值的包络图，见图11。

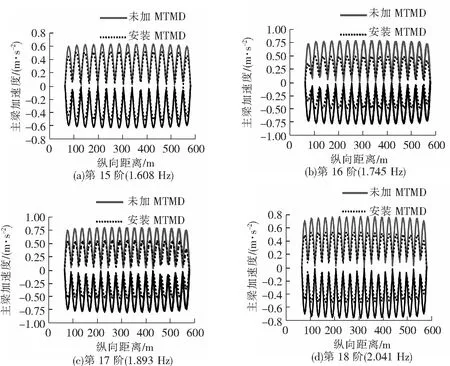
图11 有无MTMD系统时主梁加速度包络图的比较

从图11主梁各节点中提取出不同频率下的各主梁竖向加速度的最大值，见表4。

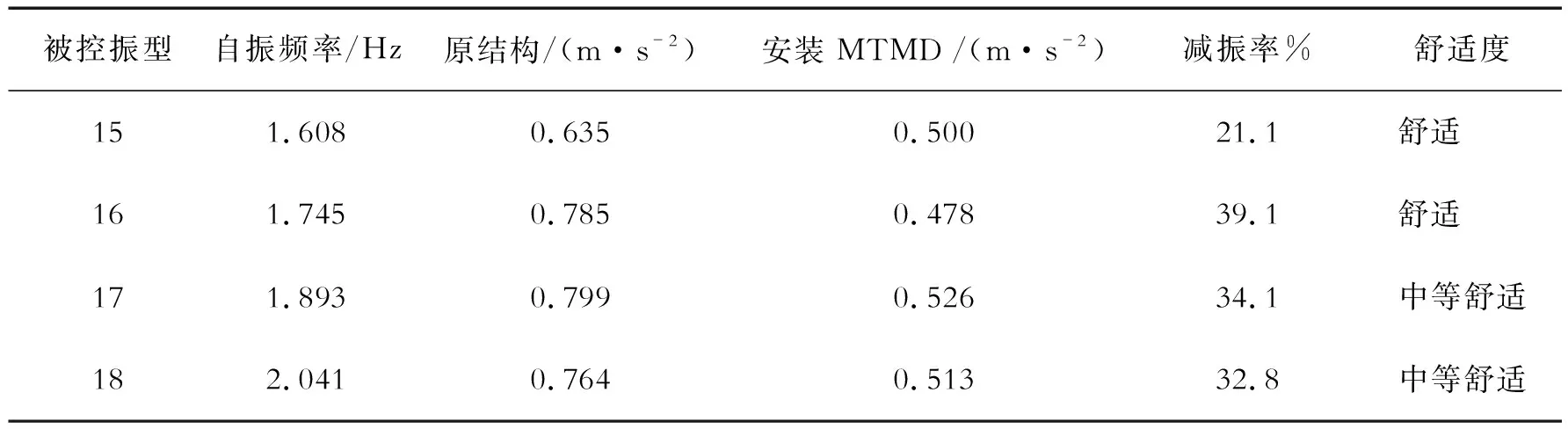
表4 安装MTMD系统后主梁最大竖向加速度

由图11和表4可以看出，在没有安装MTMD系统时，主梁节点加速度峰值沿跨度方向变化幅度很小，加速度峰值都接近1 m/s2，实际通行中行人接近不舒适的状态；安装MTMD系统后，4个频率下的主梁加速度峰值均明显下降至0.5 m/s2附近，最大竖向加速度峰值减小到初始值的60.8%，最大减振率达到39.1%，由此可以看出，MTMD系统对大跨径人行悬索桥的减振响应效果明显。

5 结论

以某大跨径人行悬索桥为研究对象，首先进行了人致振动和行人舒适度分析，然后针对竖向舒适度较差的问题，采用多重调谐质量阻尼器装置MTMD进行了减振分析，主要结果如下：

(1)主梁加速度极值随行人密度的增加而增大，计入人群质量后加速度极值下降。行人步频取桥梁不同阶固有频率时引起的主梁加速度极值受加载模态形状和不同步频时所对应的荷载折减系数ψ的影响。

(2)随MTMD系统各参数比例系数的增加，主梁竖向加速度最大值减小，减振率增大，但最优的刚度、质量和阻尼需根据减振率和系统总质量综合确定。

(3)安装MTMD系统后，人行悬索桥受控频率下的主梁加速度峰值均明显下降，最大减振率达到39.1%，可以看出，MTMD系统对人行悬索桥的减振效果明显。