一种ω型弹条扣件扣压力的锤击测量方法研究

王立敏, 张青云

(1. 中国铁路北京局集团有限公司 唐山工务段, 河北 唐山 064000;2. 石家庄铁道大学 机械工程学院, 河北 石家庄 050043)

0 引言

弹条扣件系统是用于保障钢轨与轨枕连接的重要结构，是扣压力的主要来源，目的是防止钢轨在工作过程中发生翻转和错位。长期工作的扣件系统难免会发生松动甚至损坏，扣件扣压力失效会增大钢轨振动[1]，存在严重的安全隐患。因此，及时测量扣件扣压力并发现扣压力不足的扣件，对列车行车安全具有重要意义。

现有的扣件扣压力测量方法主要为提拉法，但是这种方法需要复杂的安装过程，工作量较大且检测精度不好控制[2-3]。国内外近年来在分析扣件或螺栓受力与振动模态的关系方面开展了大量研究，如王绍华等[4]和崔树坤等[5]分别通过振动模态法研究了Ⅲ型弹条扣件和WJ-8型扣件的工作状态；李中等[6]利用有限元仿真建立了Vossloh300-1型扣件系统螺栓应力、弹条应力与扣压力关系曲线；Li et al[7]基于扣件系统的动态刚度模型，研究了WJ-2A型扣件的载荷和频率依赖关系；Mohammad et al[8]提出了一种基于最优小波变换的轨道扣件系统模态参数识别方法；Naoki et al[9]的研究表明，通过测量螺母伸出的螺栓螺纹部分的弯曲模态固有频率，可以得到螺栓/螺母组件上的轴向力。

以振动测试弹条固有频率为基础，利用COMSOL软件建立有限元模型，仿真研究弹条扣件系统预紧扭矩、扣压力以及固有频率之间的关系，之后设计试验台装置，开展弹条扣件受锤击后的振动参数测试与分析试验，得到扣件系统固有频率与扣压力的拟合公式，进一步考虑现场操作可行性与测量准确性需要，提出了ω型弹条扣件扣压力锤击法测量的合适激振位置和角度。

1 测量原理

结构的应力和变形对结构整体的模态特征有着不容忽视的影响，因此利用振动模态分析技术可以对受力结构的工作状态进行检测。ω型弹条扣件的扣压力源于螺栓的预紧力，此过程会导致弹条、螺栓和轨距挡板等多个部件产生应力。

在弹条扣件模型中结构可视为自由振动模式，阻尼对振动的影响可以忽略，因此振动微分方程可写为[10]

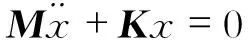
(1)

式中,M为质量矩阵;K为刚度矩阵。当弹条扣件处于预紧工作状态时，扣件系统的整体刚度矩阵K会发生改变，在此将改变量定为ΔK。因此工作状态下扣件系统的振动微分方程变为

(2)

进一步可变换转化成

(ω2+Δω2)Iφ=(K+ΔK)φ/M

(3)

可提取出固有频率平方项的偏移值与扣件系统刚度矩阵改变项的关系为

Δω2Iφ=ΔKφ/M

(4)

由此表明，对于φ≠0的非零振动形式来讲，固有频率与刚度矩阵存在必要联系。因此找到固有频率与弹条扣件扣压力的对应关系，即可判别弹条扣件的工作状态。

2 扣件扣压力仿真模拟

2.1 模型构建

设计弹条扣件试验台并等比例建立仿真模型。对部分零部件的接触面做了微变形处理，以模拟扣件系统长期在大载荷作用下结构的塑性形变，同时还可以使接触更加平顺，避免作用力过度集中。经过多次调试确定将弹条及轨距挡板等重要部件以最小1 mm划分四面体网格，曲率因子为0.6，条状部件采用扫掠的方式划分网格，模型共包含117 260个域单元，扣件试验台仿真模型如图1所示。

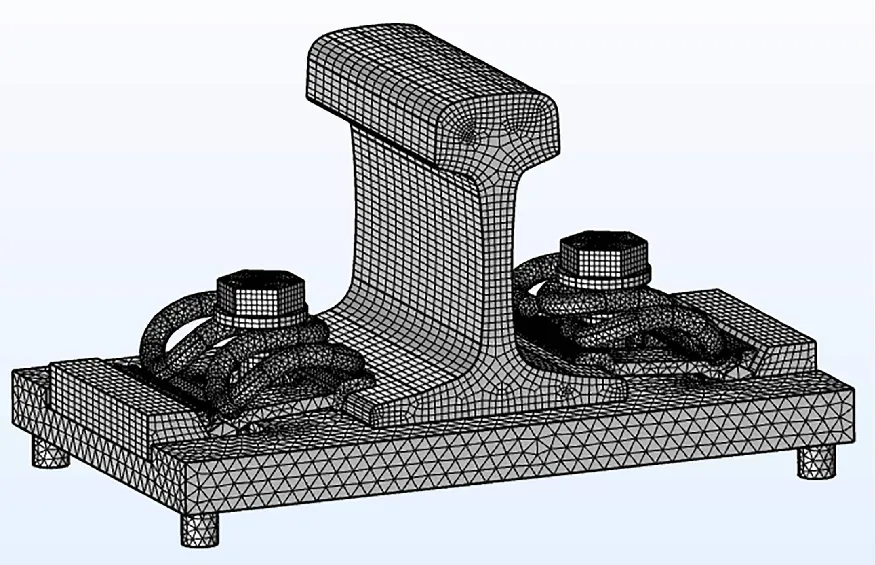
图1 弹条扣件试验台仿真模型

2.2 材料设置

扣件系统除尼龙挡板座外其他构件均由不同性质的钢材制成。弹条原材料为50Si2Cr或不低于其性能的热轧钢，材料性能满足GB/T 1222—2016的规定。轨距挡板采用铁路用热轧轨距挡板型钢且满足文献[11]要求，使用M24标准螺栓作为道钉螺栓配合垫片实现扣件的预紧。扣件系统各构件材料参数如表1所示。

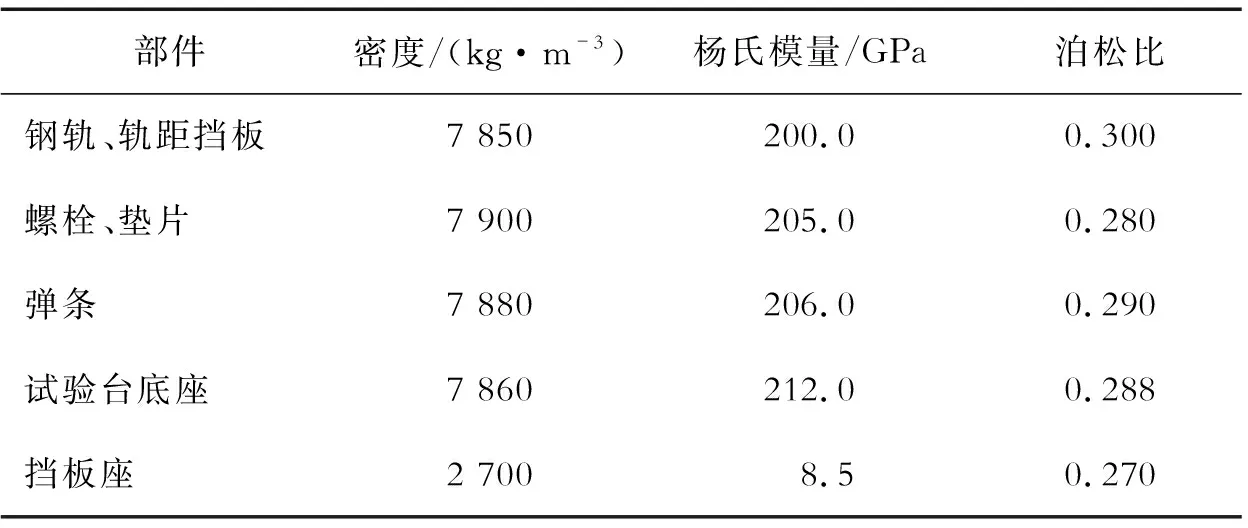
表1 扣件系统各构件的材料参数

2.3 计算结果

当螺栓的预紧扭矩分别为40、80、120、160 N·m，另一侧预紧扭矩为60 N·m时，通过仿真计算可得扣件系统的应力分布如图2所示。调整不同方向载荷的分量和相位可以模拟出不同角度的锤击效果。从计算结果可看出，ω型弹条应力中间两内臂的应力值最大，相对而言外臂的应力小一些。随着螺栓预紧扭矩的增加，弹条扣件的扣压力会随之呈近似线性增大，与此同时弹条固有频率也会出现线性上升趋势，其关系曲线如图3所示。

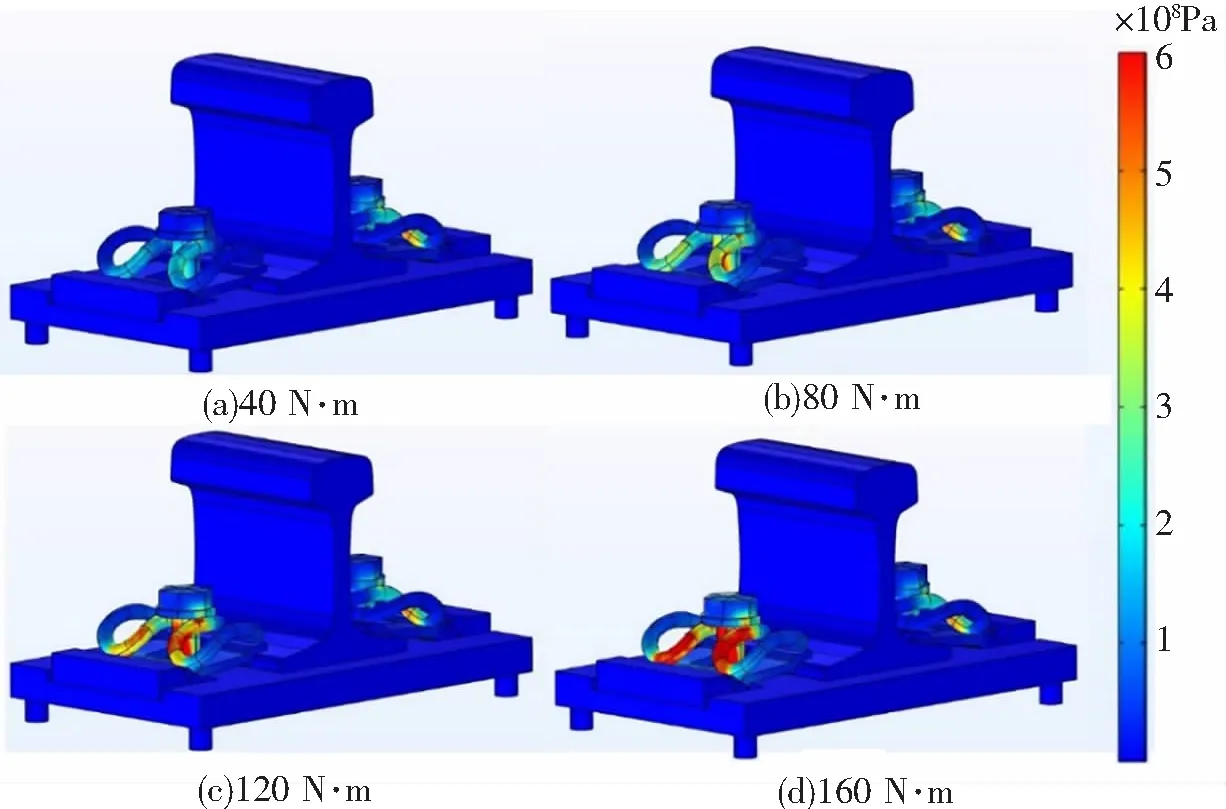
图2 不同预紧扭矩下扣件系统的应力分布图

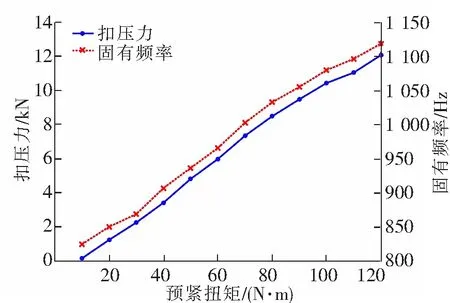
图3 弹条扣压力和固有频率与螺栓预紧扭矩之间的关系

2.4 模拟分析

ω型弹条内部应力随预紧载荷的增加而增加，并且弹条两内臂的应力相比外臂有更为明显的受力趋势。这是因为弹条与螺帽、垫片的接触位置处于中间部分，弹条内臂可以最大限度传递来自螺栓的预紧载荷；除此以外，轨距挡板的形状以及布置也是产生内臂应力明显较大现象的原因之一。

由于扣件的扣压力与来自螺栓的压力直接相关，并且理想状况下螺栓的预紧扭矩与螺栓的工作力可认为存在线性关系，因此扣压力与预紧扭矩也近似存在线性关系。在扣件稳态分析中，弹条内部产生应力和变形，其固有频率存在相应的偏移也与预期结果相符。

分别模拟与竖直方向成0°、20°和40°的角度激励弹条外臂顶端的情况，以0°激励得到的垂直振幅为基准，三者垂直振幅的综合评估为100%、97.9%和88.4%，验证了针对实验垂直激励为优选方案的结论。模拟结果证明激励强度会影响振动信号的强度，但没有明显的线性规律，结合应用场景和测量流程，激励力度只需满足传感器的接收条件即可。值得一提的是激励条件对服役弹条的固有频率几乎不产生影响。

3 锤击法扣压力测试

3.1 试验装置

将弹条安放在钢轨两侧，由电子扭力扳手拧紧螺栓使弹条处于工作状态并记录预紧扭矩。力锤敲击弹条一侧外臂以激励弹条产生振动，加速度传感器吸附在另一侧外臂用于接收振动信号。压力传感器位于钢轨底部靠近弹条趾端处测量扣压力。弹条扣件试验台与传感器布置如图4所示。

图4 试验台与传感器布置图

3.2 试验方法与数据

在钢轨一侧布置6号轨距挡板，另一侧布置10号轨距挡板。保持6号挡板扣压力约为13 kN的情况下对10号挡板的扣压力以及固有频率进行测量。试验时，用电子扭力扳手缓慢拧紧螺栓，当预紧扭矩达到加载要求时静止5 min，待受力稳定后用力锤敲击一次产生振动直至自由衰减，采集振动信号并进行特征频率分析。试验数据如表2所示。

表2 不同预紧扭矩下扣压力与固有频率试验数据

将测得的试验数据进行线性拟合，得到扣件系统弹条扣压力与螺栓预紧扭矩的关系为

F=115.095 9T-1 001.858 3

(5)

式(5)线性相关系数R2为0.932 3。扣件系统的固有频率与扣压力的拟合公式为

f=0.021 3F+810.716 4

(6)

式(6)线性相关系数R2为0.924 4。

3.3 试验分析

通过锤击法试验表明，弹条扣件系统的固有频率会随着弹条受力和变形的加剧而增加，这与仿真计算得到的关系基本一致，由此从理论和试验上均表明锤击法测量弹条扣件扣压力的方法是可行的。

考虑到人为锤击时敲击的位置、角度和力度不同均可能带来测量误差，因而采用有限元软件模拟出锤击激振力的不同场景，并对比分析振动信号和固有频率数据。结合仿真研究和试验操作表明,激振力幅值大小不影响固有频率的检测结果，通过总结经验结合项目所开发的恒定激励装置要求，拟定锤击的最大激振峰值约10 N即可，现场操作时由测试人员自行把控，数据可供参考；锤击的位置和角度在一定程度上影响振动信号的质量，选择弹条外臂顶部位置竖直向下锤击可得到较好的测量效果。

此外，弹条扣件系统的固有频率还受其他因素影响，如螺栓的润滑情况、测量现场的温度、异侧扣件的工作情况等，试验过程中发现，扣件若安装不规范对扣压力的测量精度影响较大。

4 结论

从模拟仿真和试验操作两方面对弹条扣件扣压力锤击测量方法进行研究，结果表明：

(1)在试验测量范围内弹条扣件系统的固有频率均在800～1 100 Hz，扣件系统线上正常工作状态的固有频率也基本维持在1 000 Hz左右。

(2)弹条扣件系统的预紧扭矩、扣压力以及系统的固有频率之间存在近似正比关系，通过拟合公式可由固有频率推算出扣压力值。

(3)机械锤击点和振动信号接收点最好选择在弹条的2个外臂顶端，此处振动灵敏度相对较高，以垂直向下的角度锤击会使弹条的振动更规则，锤击激振力的峰值大小不影响扣压力测量结果。