基于IRT理论的中学数学建模素养测试与评价
2022-09-20李祖漾陈雪东
李祖漾,柳 淳,金 郅,陈雪东
(湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
数学建模是新课标改革提出的中学数学六大核心素养[1]之一,其思想方法和教学内容渗透于中学数学和其他相关学科的学习与生活中,它既是应用数学解决实际问题的基本手段,又是推动数学发展的动力.但在具体的教学实践和能力培养过程中,还存在着测试方法欠缺、评价手段单一等问题.一方面,中学数学知识内容虽多,但与数学建模相关的知识体系还不够完整、精炼;另一方面,数学建模能力的测试与传统数学相比有很大差异,在智能教育相关领域的应用方面依然存在不足.
本文结合中学数学建模的教学过程[2],从若干个不同知识点角度设计测试卷,关注不同的提升路径和递进过程,有针对性地为学生提供能力变化的可能路线与评价方案,让学生清晰了解自身与数学建模素养有关的能力状况,并对薄弱知识点进行针对性的复习巩固,从而为构建智能化、个性化的学习认知框架和因材施教的测试评价体系奠定基础.学生数学建模素养能力变化影响研究思路见图1.
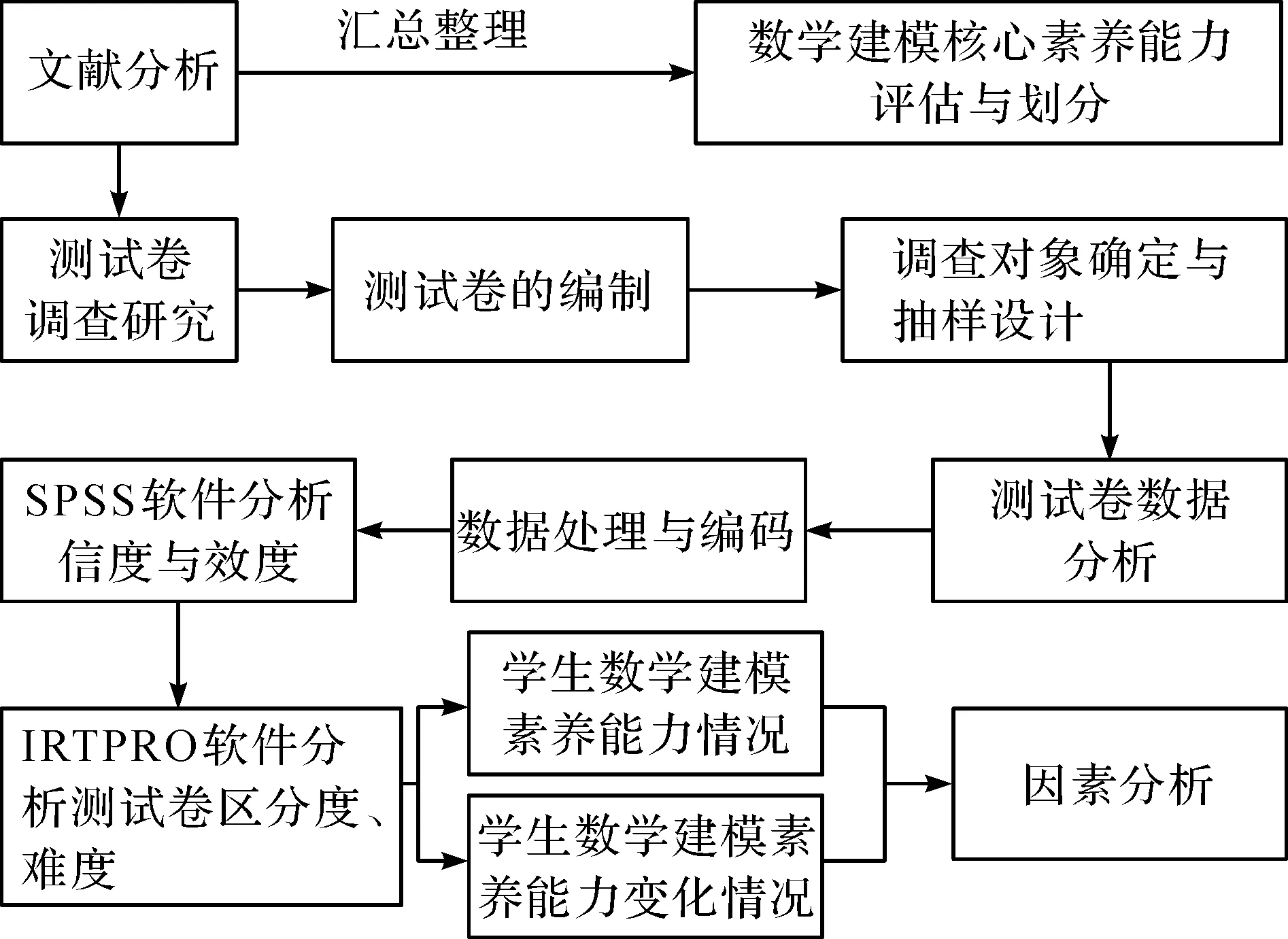
图1 学生数学建模素养能力变化影响研究思路Fig.1 Research ideas on the influence of changes in students’ mathematical modeling literacy ability
1 相关背景与理论
1.1 IRT理论
项目反应理论(Item Response Theory,IRT),又称潜在特质理论,其假设每个被试均有一种潜在特质,并通过测试实现对该潜在特质的量化估算.如在测试中,学生的某种能力或素养与某次特定的测验结果有关,且可通过概率函数加以描述.项目反应函数以概率函数的形式刻画项目作答反应与潜在特质之间的关系,其依据计分方式可分为两类:二级计分模型和分级计分模型.其中,二级计分模型多用于客观题的测试,以0和1区别作答的正确与否,其按照参数的数量进行分类,可分为单参数逻辑斯蒂模型(1PL)、双参数逻辑斯蒂模型(2PL)、三参数逻辑斯蒂模型(3PL);分级计分模型适用于项目有等级之分的情形,常用于主观题的测试,并根据得分情况进行等级划分[3].
本文以双参数逻辑斯蒂模型为例.假设被试对作答项目无猜测现象,即猜对概率为0,其模型有两个参数,分别为项目区分度参数a和难度参数b.双参数逻辑斯蒂模型的表达式为:
(1)
其中,θj为第j个被试的潜在特质,pij(θj)为第j个被试在第i个项目中答对的概率,d=-1.7是一个常数,ai为项目i的区分度参数,bi为项目i的难度参数.分别选取a=4,b=-0.97;a=0.78,b=-0.41;a=1.39,b=0,双参数逻辑斯蒂模型示意图见图2.

图2 双参数逻辑斯蒂模型示意图Fig.2 Schematic diagram of a two-parameter logistic model
分级计分模型是在双参数逻辑斯蒂模型的基础上,对项目等级进行分类,其表达式为:
(2)
其中,pijk(θj)为第j个被试在第i个项目中得k分的概率,αi为第i个项目的区分度,βik为第i个项目得k分时的难度.
本文构建的测试模型和数据分析方法主要基于双参数逻辑斯蒂模型与分级计分模型[4].
1.2 数学建模核心素养
数学模型是对现实世界内在规律的数学刻画或表示,即在研究现实世界的某个对象时,明确研究目的,并对问题作必要的简化假设,然后建立适当的数学表达式.而数学建模则是一个从现实出发,对实际问题作出一些必要的假设后将其精炼成数学模型,并利用数学方法和现代计算机工具加以解决,最后验证模型合理性的过程.目前,数学建模已纳入中学数学新课标设定的六大核心素养.数学建模核心素养要求学生应具备以下3种能力:①学生能够在实际情境中发现和提出问题,并能够针对问题建立数学模型;②学生能够运用数学知识求解模型,并尝试基于现实背景验证和完善模型;③学生应具备较强的应用能力和创新意识.
可见,中学生数学建模核心素养体现在其发现问题、归纳模型、求解方法、创新应用等多方面,且数学建模核心素养的培养与数学建模的全过程息息相关.因此,合理构建中学生数学建模核心素养的测试体系和评价方法,具有一定的理论价值和实际意义.基于该研究问题的实质与相关理论的特征,本文采用IRT理论来进行对比研究.
2 中学数学建模素养的测试与评价方法
2.1 数学建模素养测评依据
在文献阅读和分析[5-7]的基础上,结合2011年义务教育数学课程标准进行汇总和整理,得出较为准确的中学生数学建模核心素养能力评估的3个方向,即建立数学模型的能力、求解并验证数学模型的能力和应用创新的能力,并将其分别记为:能力1、能力2和能力3.在编制测试卷的过程中充分融入这3类能力的考察内容.例如:构建一次函数模型、书写函数表达式等试题可以测试学生的第1类能力;通过数学运算求解具体数值、验证所得表达式是否符合生活实际等试题可以测试学生的第2类能力;灵活创新地进行模型的实际应用等试题可以测试学生的第3类能力.
2.2 测试卷编制与评价框架构建
结合新课标数学建模能力考察的例题,以及数学建模能力考察的相关文献[8-9],编制中学数学建模素养测试卷.测试卷分为卷I和卷II,每份测试卷有A、B、C 3组题,其中卷I以客观题为主.每位参与测试的学生均需完成卷I的测试,在卷I测试结束后学生会收到相应的测试结果,然后进入卷II的测试.卷II以主观设计题为主,每位学生可根据卷I的测试结果,从A、B、C 3组题中任选一组题进行测试.在处理数据时,按照数学建模3方面的能力对题目进行分类.构建的测试卷评价框架如图3所示.
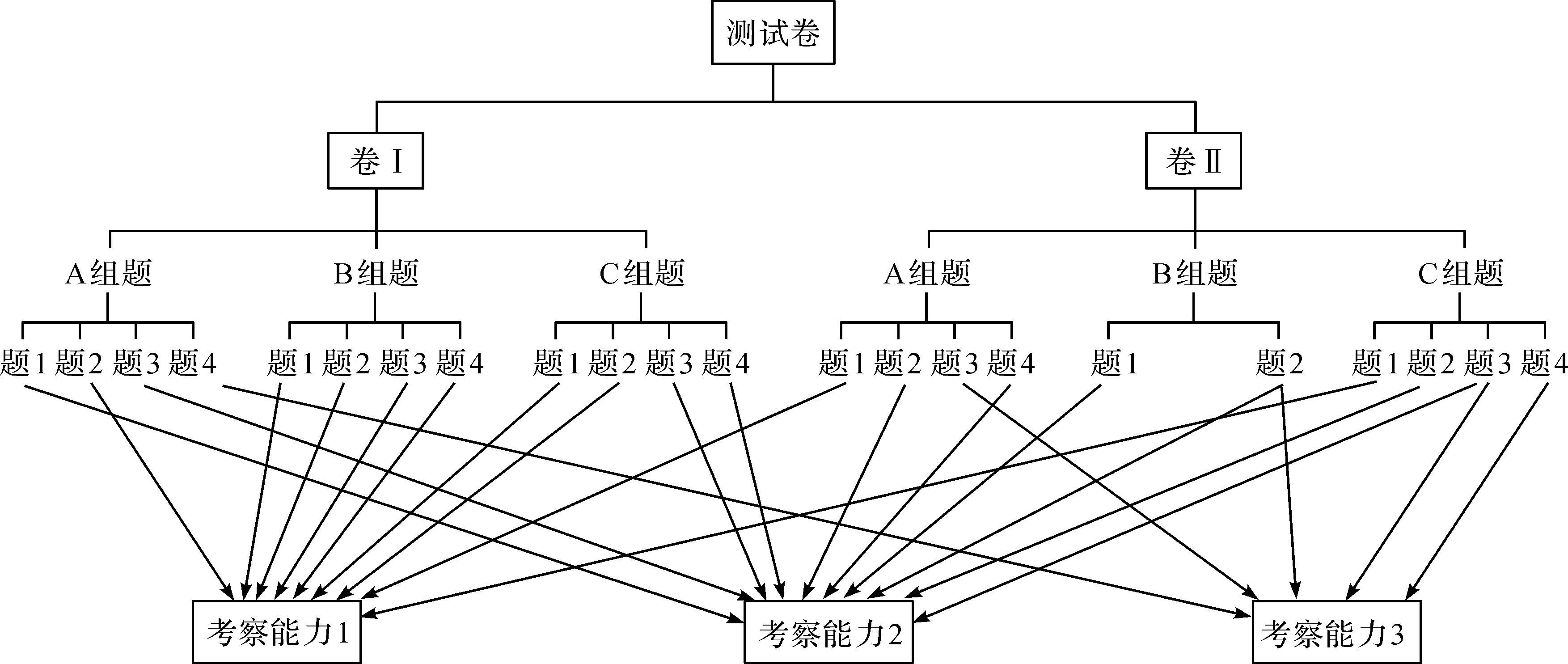
图3 测试卷评价框架图Tab.3 Test paper evaluation framework diagram
图3呈现了卷I和卷II各组题主要考察的能力分布情况.能力1和能力2的考察试题主要来自卷I,也涉及卷II,能力3的考察试题绝大多数来自卷II.从卷I到卷II,试题的难度逐步提升,考察的能力层次也逐渐提高.这有助于更深入地解读中学学生数学建模核心素养的能力及其变化情况.
2.3 测评对象与测试卷发放
测评对象为湖州市吴兴实验中学初三年级1个班级的全体学生、余姚市第四中学高三年级2个分别偏文和偏理班级的全体学生和湖州师范学院理学院大一全体学生.测验对象层次有高有低,但都具有基本的数学素养和一定的研究价值.
数学建模素养测试卷的发放采取线上与线下相结合的方式,共发放问卷440份,回收问卷440份.测试卷回收后,根据调查目的、调查对象和调查范围等要求,剔除无效测试卷,最终确定有效测试卷427份,有效回收率为97%.
2.4 测试卷的信度和效度
按A、B、C 3组题,使用SPSS测量测试卷数据的信度质量水平.结果发现,α系数均大于0.65,说明测试卷信度好,测试数据具有较高的可靠性.
按A、B、C 3组题,使用SPSS计算测试卷数据的KMO值,并进行Bartlett’s球形检验.结果发现,KMO值大于0.7,且在显著性水平0.05下,Bartlett’s球形检验观测的P值小于0.05.通过检验,说明测试卷的效度高,测试试题设置合理.
2.5 IRT分析模型的选择与系数拟合
以A组题考察能力1的题目为例,按题型要求和学生得分情况,分别使用2PL模型和分级计分模型进行项目参数估计[10].
首先,使用2PL模型对客观题进行项目参数估计,结果如表1所示.由表1可以看出,Item6的估计误差过大,其原因是该类题做错的人数极少,难度系数和区分度低,且Item 3到Item 10考察的知识点及素养情况一致,而Item 6的估计值与预期值差距过大,从而导致Item 6的估计误差过大.
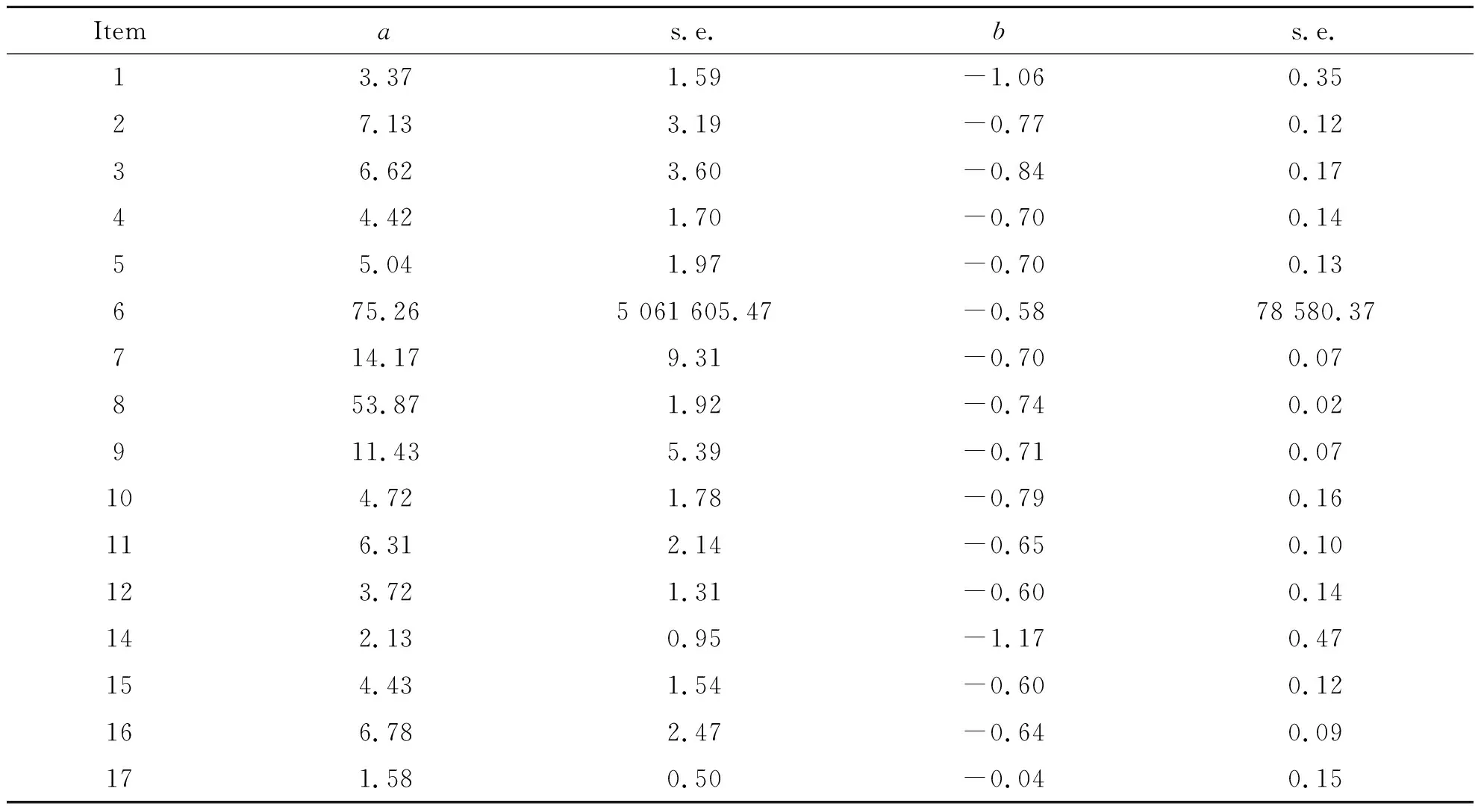
表1 A类题考察能力1 题目的2PL模型项目参数估计表
其次,使用分级计分模型对主观题进行项目参数估计,结果如表2所示.

表2 A类题考察能力1题目的分级模型项目参数估计表
最后,基于2PL模型和分级计分模型,对其余测试题目进行项目参数估计,得出区分度、难度等参数估计,以便后续对学生数学建模素养水平情况进行分析.
3 结果与分析
3.1 学生数学建模素养水平
3.1.1 作答A组题学生的数学建模素养水平
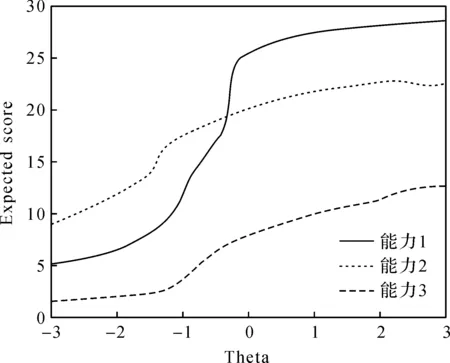
根据IRT理论进行模型选择与系数拟合,分别得到作答A组题的学生在能力1、能力2和能力3的测试特征曲线,如图4所示.

图4 A组题测试特征曲线图Fig.4 Characteristic curve chart of test paper A
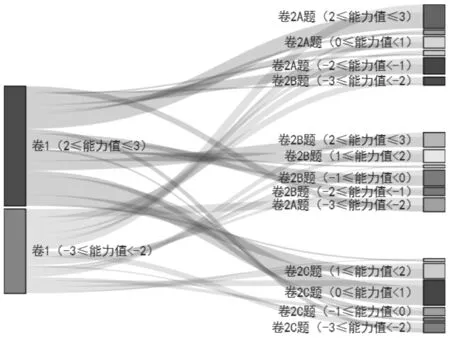
由图4可以看出,能力1的特征曲线拐点位于较低水平区间(-1 3.1.2 作答B组题学生的数学建模素养水平 根据IRT理论进行模型选择与系数拟合,分别得到作答B组题的学生在能力1、能力2和能力3方面的测试特征曲线,如图5所示. 图5 B组题测试特征曲线图Fig.5 Characteristic curve chart of test paper B 由图5可以看出,能力1的特征曲线拐点位于较低水平区间(-1 3.1.3 作答C组题学生的数学建模素养水平 根据IRT理论进行模型选择与系数拟合,分别得到作答C组题的学生在能力1、能力2和能力3的测试特征曲线,如图6所示. 图6 C组题测试特征曲线图Fig.6 Characteristic curve chart of test paper C 由图6可以看出,能力1的特征曲线拐点位于较低水平区间(-1 3.1.4 学生数学建模素养水平的抽样分析 选取作答A、B、C3组题的部分学生,分别计算其在能力1、能力2和能力3的水平量化值,结果如表3所示. 表3 学生数学建模素养水平抽样分析表 由作答A组题的3位学生能力情况可以看出,3位学生的数学建模素养水平有高有低.编号20的学生的总体能力水平比其他两位学生强,即该学生的数学建模素养水平相对较高.编号100的学生的总体能力水平居中,但该学生的能力3水平最高,其余两种能力也基本达到中等水平.编号60的学生的总体能力水平最低,该学生的3种能力基本在偏下水平. 由作答B组题的3位学生能力情况可以看出,3位学生的总体能力水平均不高,尤其是能力3水平相对较欠缺. 由作答C组题的3位学生能力情况可以看出,3位学生的数学建模素养水平有高有低.编号20的学生的总体能力水平较其他学生高,3种能力普遍位于偏上水平.编号60的学生的总体能力水平较低,能力1和能力2处于中下水平,且能力3处于最低值. 从总体看,被抽取学生的平均实力居中等水平,符合抽样调查预期情况. 本文通过分析学生前后两次作答数据,并使用桑基图清晰刻画学生前后两次作答情况,以分析学生数学建模素养水平变化情况. 对学生作答卷I与卷II的能力1变化情况进行统计分析,得到的桑基图如图7所示. 图7 被试作答卷I和卷II的能力1变化桑基图Fig.7 Sankey diagram of the change of the participant ability 1 in answering test paper I and test paper II 由图7可以看出,在卷I的测试中,将近60%学生的能力1水平低于中间值;在卷II A组题的测试中,学生的能力1水平明显提升,在卷II B、C组题的测试中也有类似现象;在卷I测试中能力1较好的学生,其在卷II测试中的能力1水平高低均有分布,在卷I测试中能力1欠缺的部分学生,其在卷II测试中的能力1水平明显提升. 对学生作答卷I和卷II的能力2变化情况进行统计分析,得到的桑基图如图8所示. 由图8可以看出,在卷I的测试中,将近60%学生的能力2低于中间水平;在卷II的测试中,学生的能力2水平主要分布在中等,尤其在B、C组题的测试中,大部分学生的能力2水平处于中间上下浮动状态;在卷II测试中能力2较好的大部分学生,其在卷I测试中的能力2水平也较好,在卷I测试中能力2欠缺的少数学生,其在卷II测试中的能力2水平较优异. 对学生作答卷I与卷II的能力3变化情况进行统计分析,得到的桑基图如图9所示. 图8 被试作答I卷和II卷的能力2变化桑基图Fig.8 Sankey diagram of the change of the participant ability 2 in answering test paper I and test paper II 图9 被试作答I卷和II卷的能力3变化桑基图Fig.9 Sankey diagram of the change of the participant ability 3 in answering test paper I and test paper II 由图9可以看出,在卷II的测试中,学生的能力3水平分布较均匀;在卷I测试中,能力3水平较高的大多数学生,其在卷II测试中的能力3水平仍旧较高;在卷I测试中,能力3欠缺的少数学生,其在卷II测试中的能力3水平仍较优. 由图7至图9可以看出,在卷I的测试中,学生的能力测验结果分布出现断层,即中等能力的学生较少,低等能力和高等能力的学生较多.在卷I测试中,能力较好的学生在卷II测试中,其能力仍较好,也有少数在卷I测试中能力不高的学生,其在卷II测试中能力较好.总体而言,在两份测试卷中绝大部分学生的能力变化较为均衡. 数学建模渗透于中学数学和其他相关学科中[11].但在实际教学过程中,仍存在着测试方法欠缺、评价手段单一等问题.本文基于IRT理论构建学生数学建模能力及其变化情况测评方法,并在测评时考虑试题的难度、区分度等指标,使其对学生数学建模能力的测评更具客观性和合理性,从而为设计因人专设的自适应数学建模能力测试系统提供支撑.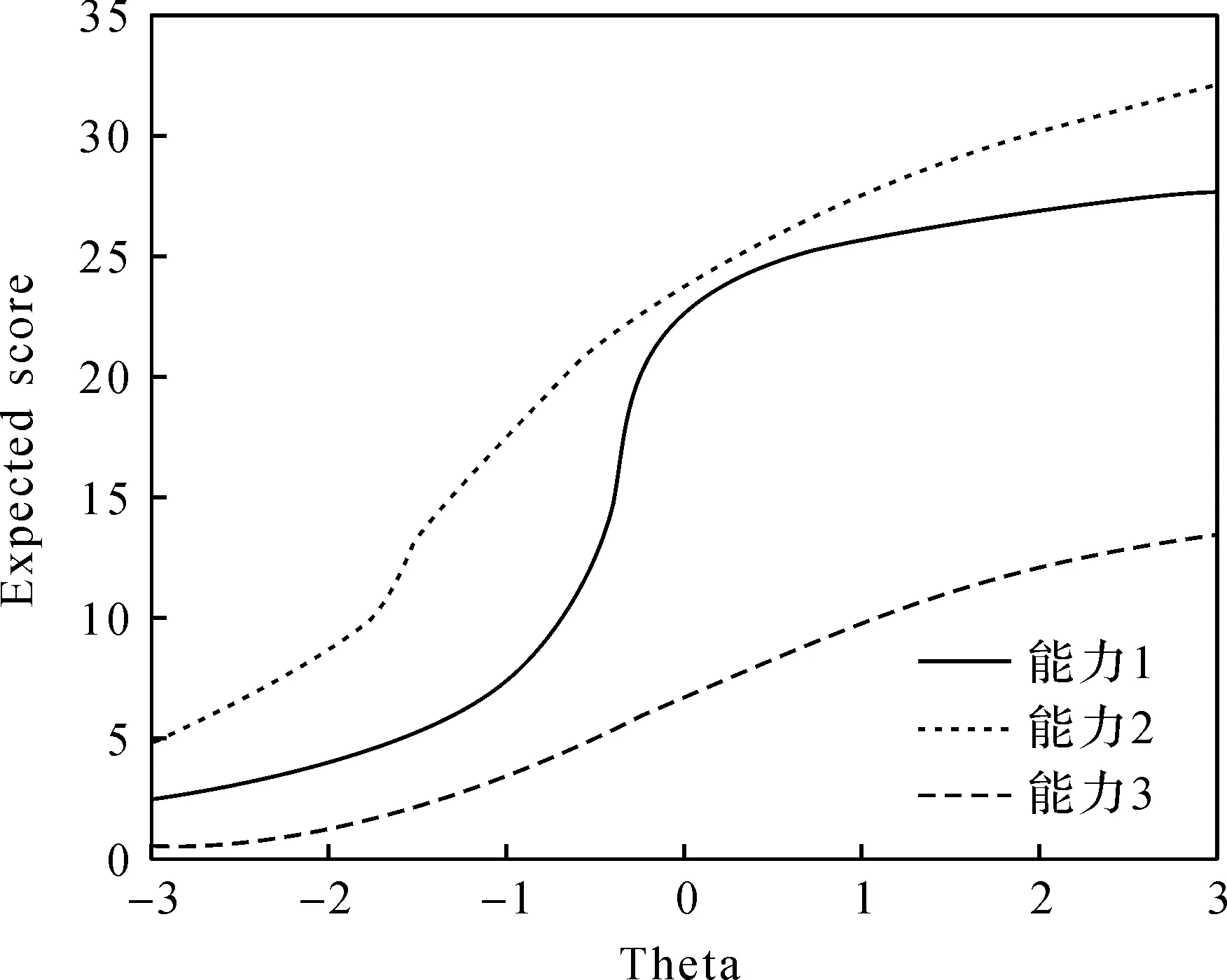

3.2 学生数学建模素养水平变化情况


4 结 论
