改进的最小二乘孪生支持向量机聚类

刘玉菲，陈素根

（安庆师范大学 数理学院，安徽 安庆 246133）

聚类是一种重要的机器学习方法，如基于划分的聚类K-means 算法、基于密度的聚类DBSCAN 算法、基于层次的聚类AGNES算法等[1]。近年来，基于平面的聚类引起学者们的关注，P.S Bradley等提出的k平面聚类（KPC）[2]算法，其主要思想是通过平面更新代替聚类中心更新，但是KPC忽视了每一类之间的影响。为了克服类与类之间对聚类效果的影响，Wang等提出了孪生支持向量机聚类（TWSVC），其主要思想是在寻找簇中心平面时要求本簇样本尽可能近，而非本簇样本与该平面有一定距离[3]。随后，许多学者在TWSVC的基础上提出了改进的算法，如Wang等提出的基于Ramp损失的孪生支持向量机聚类算法（Ramp TWSVC）[4]，Sanaz Moezzi 等提出的改进的孪生支持向量机聚类算法（TWSVC+）[5]等。TWSVC算法作为一种新型的聚类算法，表现出了较好的聚类性能，但它依然有一些不足，如TWSVC需要求解一系列二次规划问题，计算相对复杂。为了提高算法的求解效率，Reshma Khemchandani 等人2016 年提出了最小二乘孪生支持向量机聚类（LSTWSVC），该算法在目标函数中引入了一个正则项以实现结构风险最小化，并用等式约束代替TWSVC中不等式约束，优化问题只需要求解一系列的线性方程组，而不是像TWSVC那样求解一系列的二次规划问题，减少了计算复杂性[6]。然而，LSTWSVC对每一类样本都给予相同的惩罚，使得该算法性能受离群点的影响较大。基于上述分析，为了减少离群点对LSTWSVC性能的影响，我们构造了一种新的权重函数，并在此基础上提出了一种改进的最小二乘孪生支持向量机聚类算法，简记为ILSTWSVC。

1 相关工作

给定m个n维的数据样本{x1,x2,x3,…,xm}，记为X=(x1,x2,x3,…,xm)T，为方便起见，将第i类数据样本全体记为Xi，其余类数据样本记为，其中i=1,2,3,…,k。

1.1 KPC

对于聚类问题，KPC希望将数据集X聚成k类，使数据样本点在k类中心平面的附近中心平面为

其中，wi∈Rn和bi∈R，KPC尝试解决以下问题：

其中，Xi包含X中属于第i个类的行，e表示分量全为1的适当维数向量。

求解优化问题（2），可得到wi,bi，再按照以下规则进行聚类：

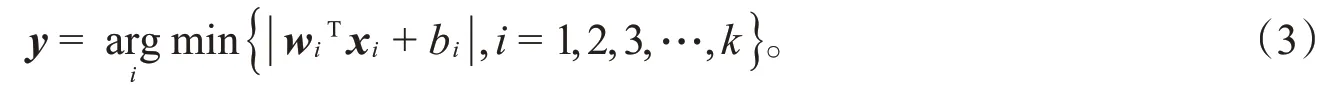
对于非线性情形，我们引入核函数K(x,X)，利用核技巧就可以直接将线性KPC模型推广到非线性KPC模型，具体算法见参考文献[2]。

1.2 TWSVC

对于孪生支持向量机聚类问题，TWSVC寻找k类中心平面为

对于每一类，使得这一类的数据点尽可能离这一类中心平面近，其余样本点尽可能远离这一类，建立优化问题如下：

其中，c表示惩罚参数，ξi是松弛向量，e表示分量全为1的适当维数向量。

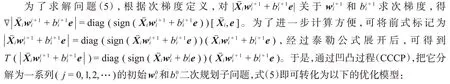
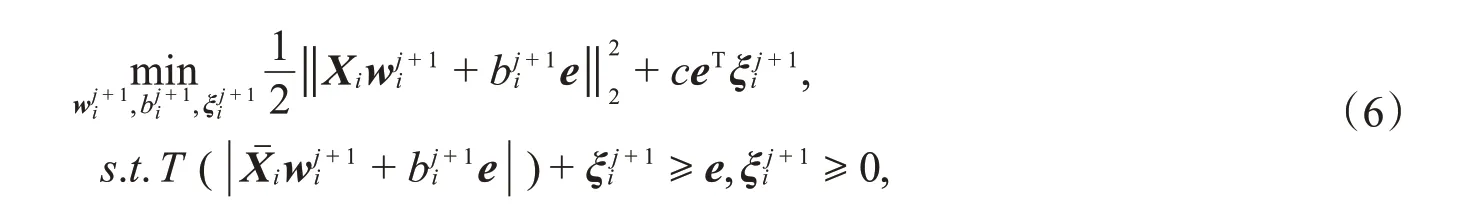
其中，T(·)表示一阶泰勒展开，j表示第j个子问题。

引入拉格朗日函数，利用Karush-Kuhn-Tucker(K.K.T)条件，得到对偶问题：

对于非线性情形，引入核函数K(x,X)，利用核技巧将线性TWSVC模型推广到非线性TWSVC模型，具体算法见参考文献[3]。

1.3 LSTWSVC

LSTWSVC用等式约束代替TWSVC中的不等式约束，并在目标函数中加入正则化项，以实现结构风险最小化原则。对于第i类(i=1,2,3,…,k)聚类中心平面，建立优化问题：

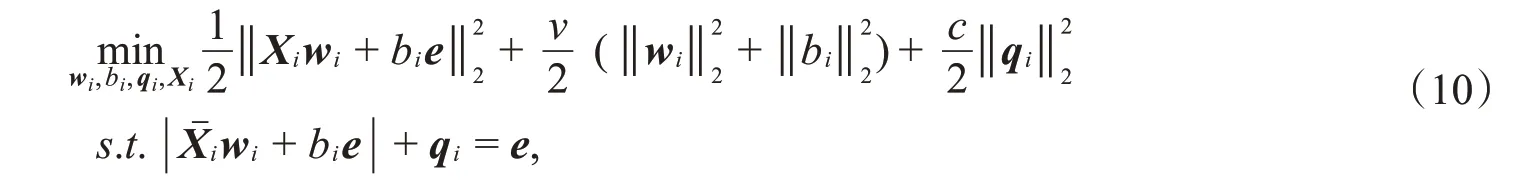
其中，c,v是参数，qi是松弛向量，e表示分量全为1的适当维数向量。

与TWSVC 类似，上式可以通过凹凸过程求解，把它分解为一系列(j=0,1,2,…)的初始二次规划子问题，（10）式即可转化为以下的优化模型：

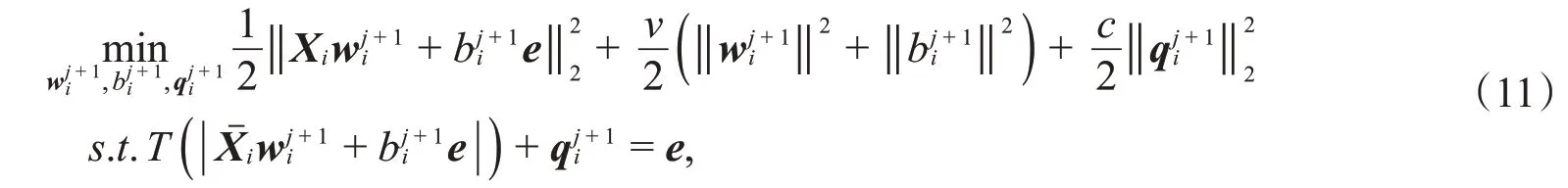
其中T(·)表示一阶泰勒展开，j表示第j个子问题。

将式（11）中的约束条件代入优化问题的目标函数中，得到无约束优化问题：

求解优化问题式（12）转化为求解线性方程组问题。对目标函数关于求导并整理化简得到以下线性方程组：

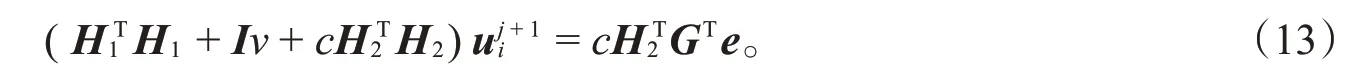
于是，求解式（13）可得

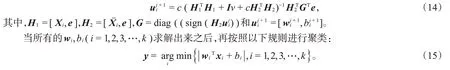
对于非线性部分，引入核函数K(x,X)，利用核技巧将线性LSTWSVC模型推广到非线性LSTWSVC模型，具体算法见文献[6]。

2 改进的最小二乘孪生支持向量机聚类

为克服离群点对LSTWSVC聚类性能的影响，本文提出了一种改进的孪生支持向量机聚类算法，简称为ILSTWSVC，下面详细介绍ILSTWSVC算法。

2.1 线性ILSTWSVC

考虑离群点对聚类效果的影响，在LSTWSVC基础上，引入加权矩阵D对其余类样本给予不同权重的惩罚，对于第i类(i=1,2,3,…,k)聚类中心平面，构建优化问题：

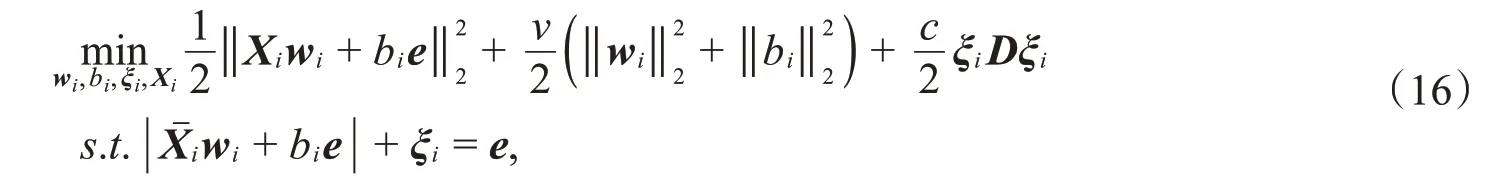
其中，c,v是参数，ξi是松弛向量，e表示分量全为1的适当维数向量，D是以di为元素的对角矩阵。

根据样本分布对聚类效果的影响，对不同的样本赋予不同的权重di：

对于优化问题（16）的目标函数，第1项是样本点到聚类中心平面的距离平方和，第2项是正则项，第3项是损失项。最小化第1项使得第i类样本更加聚集在第i类聚类中心平面周围，最小化第2项以实现结构风险避免过拟合，最小化第3项使得其他类样本尽可能与第i类聚类中心平面保持一定距离。

为了求解优化问题（16），先将其约束条件一阶泰勒展开，再用CCCP求解，对于第i类(i=1,2,3,…,k)聚类中心平面，通过给定一系列(j=0,1,2,…)的初始，优化问题（14）可转化为

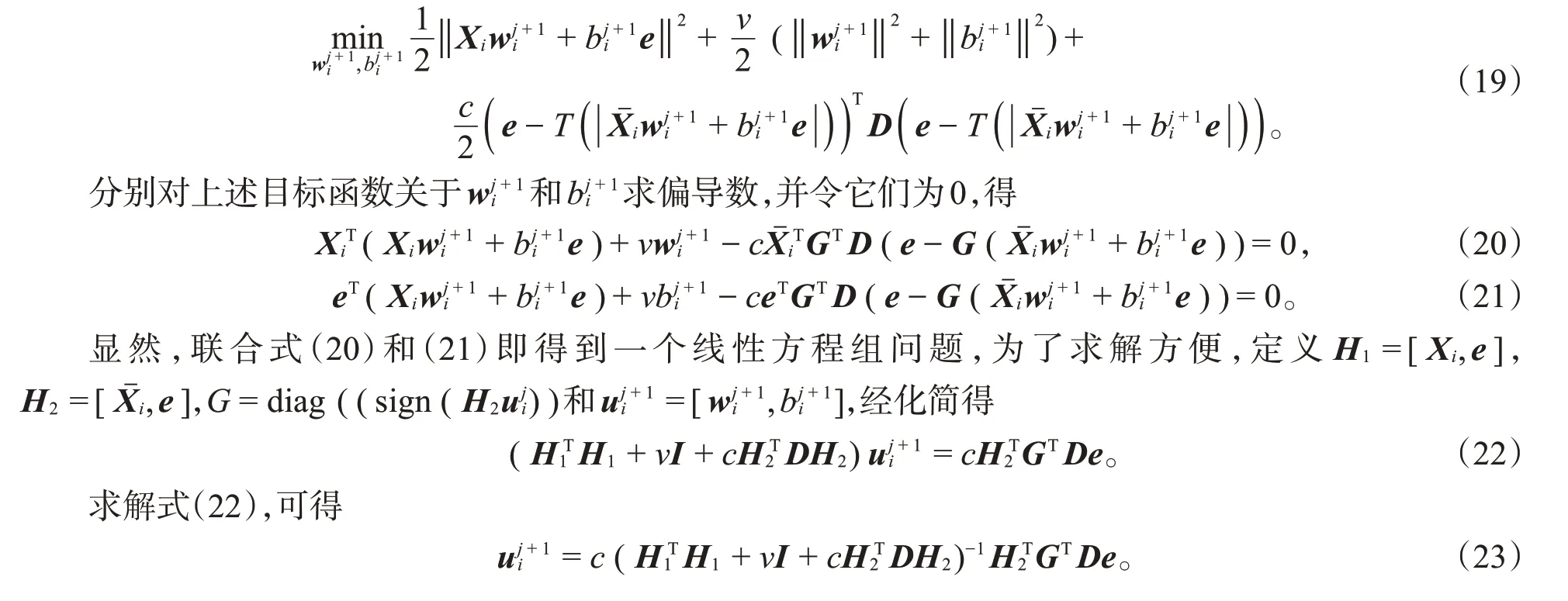
当所有的wi,bi(i=1,2,3,…,k)求解出来之后，再按照以下规则进行聚类：

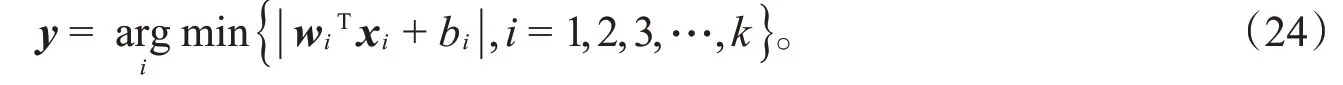
综上所述，给出线性ILSTWSVC算法如下：

算法1.线性ILSTWSVC

2.2 非线性ILSTWSVC

现将上述的线性模型拓展为非线性模型。选择合适的核函数K将数据映射到高维特征空间中，类似于线性情形，建立非线性ILSTWSVC模型的优化问题：

类似线性情况，可转化为

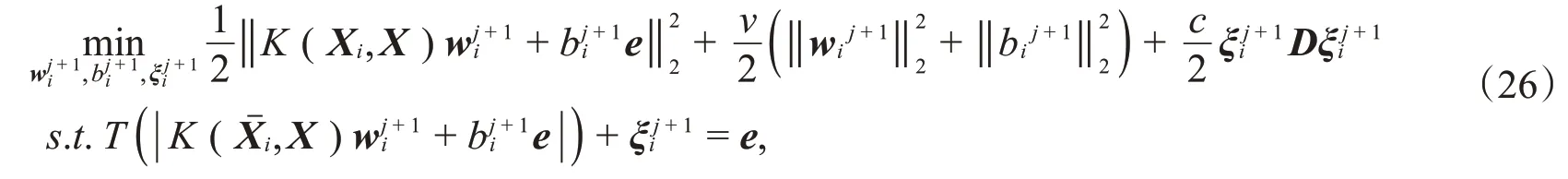
其中，c,v是参数,是松弛向量，e表示分量全为1的适当维数向量，D是对角矩阵。

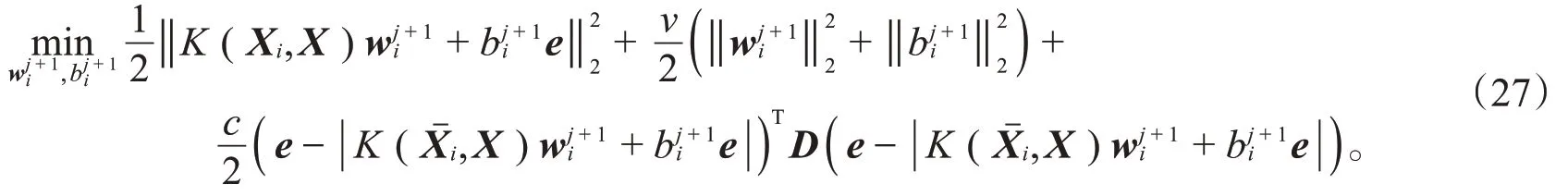
求解（27）式能得

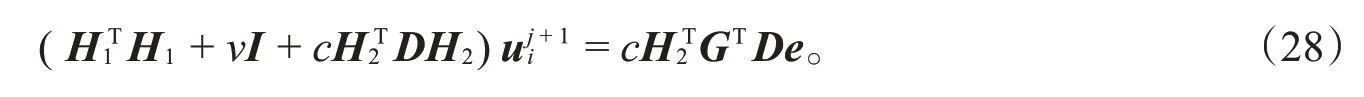
求解式（28），可得

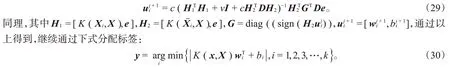
对于非线性算法，可类似于线性算法步骤，不同之处在于先选择合适的核函数K将数据映射到高维空间，此处不再赘述。

2.3 算法描述

一般情况下，基于平面的聚类算法中的初始标签是随机生成的，这样选择的实验结果往往不稳定，聚类效果对初始标签有较强的依赖性。因此，采取文献[7]中的初始化方法得到每一类的样本点Xi(i=1,2,3…,k)，然后求解特征值问题：

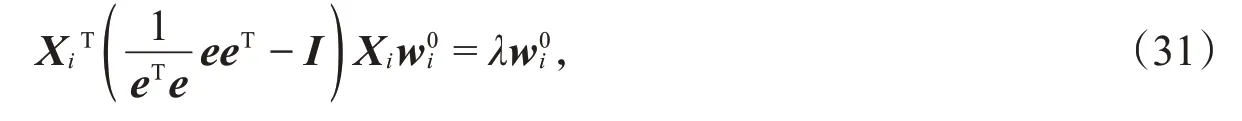
其中，I是一个单位矩阵，此处是最小特征值λ对应的特征向量，并且

3 实验结果及分析

为验证ILSTWSVC 的性能，选取2 个人工数据集和5 个UCI 数据集进行实验。具体实验环境是MATLAB R2014a，硬件配置为Window10 操作系统，12 GB 内存，3.5 GHz 主频CPU 的计算机。选取KPC、TWSVC 和LSTWSVC 作为对比实验，与ILSTWSVC 实验进行比较，非线性情形下选择核函数，其中δ为核参数。实验均采用网格寻优为各算法选择最优参数，在TWSVC、LSTWSVC和ILSTWSVC中，c和v的网格搜索范围均设置为{ 2i|i=-5,-4,-3,…,5 }，在所有非线性实验中，核函数参数δ搜索范围设置为{ 2i|i=-5,-3,-1,…,5 }。初始化的近邻数p从{ 1,3,5 }中选择。

使用准确率（Accuracy）来衡量聚类性能，给定聚类标号yi∈N,i=1,2,3,…,m，计算相应的相似矩阵M∈Rm×m，其中

设数据集的真实聚类标签计算的相似度矩阵为Mt，预测标签计算的相似矩阵为Mp。定义聚类方法的准确率为兰德统计量（Rand statistic）。

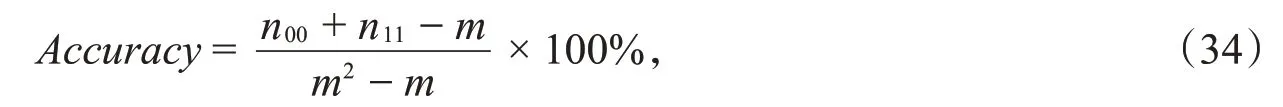
其中，n00是Mp和Mt中0的个数，n11是Mp和Mt中1的个数。

对于人工数据集，我们选择了Aggregation和Jain 这2 个数据集。算法结果中最好的指标用粗体表示。表1和表2分别给出了线性情形和非线性情形下ILSTWSVC、KPC、TWSVC、LSTWSVC在2个人工数据集上的聚类结果。

表1 线性ILSTWSVC与几种算法在人工数据集上的准确率比较

表2 非线性ILSTWSVC与几种算法在人工数据集上的准确率比较

从表1和表2可以看出，我们的方法在人工数据集Aggregation和Jain上均取得了较好的结果，在线性情形下，与其他算法相比，准确率更好。图1给出了线性情形下各算法在Jain数据集上的聚类效果图，可以看出，我们所提出的ILSTWSVC算法具有较好的聚类效果。

图1 线性情形下各算法在Jain数据集的聚类效果图。（a）原始数据图；（b）TWSVC；（c）LSTWSVC；（d）ILSTWSVC

为了进一步验证所提算法的有效性，在UCI数据集上进行实验，选择了Iris，Hamberman，Ecoil，Zoo和Glass这5个数据集进行验证。表3和表4分别给出了线性情形下和非线性情形下ILSTWSVC、KPC、TWSVC、LSTWSVC 在5 个UCI 数据集上的聚类准确率。由表3 可以看到，在UCI 数据集Iris，Hamberman，Zoo和Glass上，本文的线性ILSTWSVC具有较高的准确率。由表4可以看出，本文中所提出的非线性ILSTWSVC在大多数数据集上也取得了较好的结果。

表3 线性ILSTWSVC与KPC、TWSVC、LSTWSVC在UCI数据集上的聚类准确率比较

表4 非线性ILSTWSVC与KPC、TWSVC、LSTWSVC在UCI数据集上的聚类准确率比较

4 结论

综上所述，针对孪生支持向量机聚类算法没有考虑数据分布对聚类性能影响的问题，本文构造了一种新的权重函数以降低离群点对聚类性能的影响，从而提出了一种改进的最小二乘孪生支持向量机聚类算法（ILSTWSVC）。本算法给予样本点不同的惩罚，构造了一种新的权重函数，在人工数据集和UCI数据集上验证了ILSTWSVC 的有效性，与其他算法相比，我们的线性部分在人工数据集Aggregation，Jain和UCI数据集Iris，Hamberman，Zoo和Glass上都有较高的准确率，非线性部分在人工数据集Jain和UCI 数据集Iris，Hamberman，Ecoil，Zoo，Glass 上也都有较高的准确率。本文算法的不足之处是存在多个参数选择，如何选择最优参数以提高聚类算法性能值得进一步研究。