近似优化算法在半集中式空调系统末端优化设计中的应用
2022-09-20刘雪峰陈文鉴
刘雪峰 陈文鉴
(华南理工大学电力学院 广州 510640)
0 引言
建筑节能是我国实现碳达峰、碳中和的关键领域,公共建筑的中央空调系统能耗往往占据建筑能耗40~50%以上,而冷冻水系统能耗占集中式中央空调系统的60%以上[1,2]。目前中央空调系统的设计方式一般为通过规范设计参数对建筑进行负荷计算,根据计算结果对中央空调冷冻水系统各设备进行选型,为保证设计的可靠性,设计人员通常会盲目放大安全系数,使中央空调系统的选型偏大,造成投资成本与运行成本的浪费,故合理的末端选型对建筑节能具有重要作用。
目前,很多学者都对中央空调系统部件设计优化的问题展开研究。在对末端进行优化设计时,算法的计算效率是优化可行的必要条件,进化算法、顺序搜索算法、遗传算法(GA)、粒子群算法(PSO)、GA-PSO 组合算法等优化算法已经可以很好地对末端尺寸选型进行优化[3-7],但是遗传算法在处理多变量、非线性、参数高度耦合的末端选型设计优化问题时,会有参数合理设定困难,优化效率慢、优化收敛性差等缺点,粒子群算法收敛速度快,但是收敛精度不高,且容易陷入局部最优的困境。对于各类混合算法虽然在一定程度上可以弥补各自算法的缺点,但是算法编写与调试较复杂,且很难找到速度与精度的平衡点[8]。中央空调系统一般以全生命周期成本为评价指标[9],为提高优化算法收敛速度,研究通常使用灰箱或者黑箱的方法来简化末端、管网等部件的数学模型[7],忽略表冷器热力性能与管网水力性能对中央空调系统整体的影响,使其研究结果难以推广到大型复杂中央空调系统的应用过程中。其次,负荷分布在时间与空间上也具有不确定性,实际工程项目中很难选择到与优化结果相匹配的末端选型,这会使末端的性能偏离其设计工况,进而导致冷冻水管网的性能及系统的能耗发生改变[10],故很难根据优化结果对末端选型设计进行优化。
为此,本文提出一种近似优化算法来探究随机负荷约束下大型复杂冷冻水系统末端优化问题。根据热力平衡与水力平衡建立空调末端的热力模型和同程管网的水力模型,计算中央空调系统能源利用效率,使用随机走步变步长的近似优化算法获取大型复杂空调系统各末端的选型优化结果,并对其次优解群进行统计分析,以获得适应于不同负荷分布变化的末端设计方案,并对设计方案进行反向验证,为末端设计选型提供一些理论指导。
1 大型冷冻水系统空调末端优化模型
1.1 同程管网运行特性模型
1.1.1 同程管网拓扑结构
本文以同程管网为研究对象,同程管网包括空调末端(AHU),阀门以及连接管道等元件。同程管网的层数从底层到高层依次编号为1~k,每层的末端从近端到远端依次编号为1~n,拓扑模型如图1 所示。
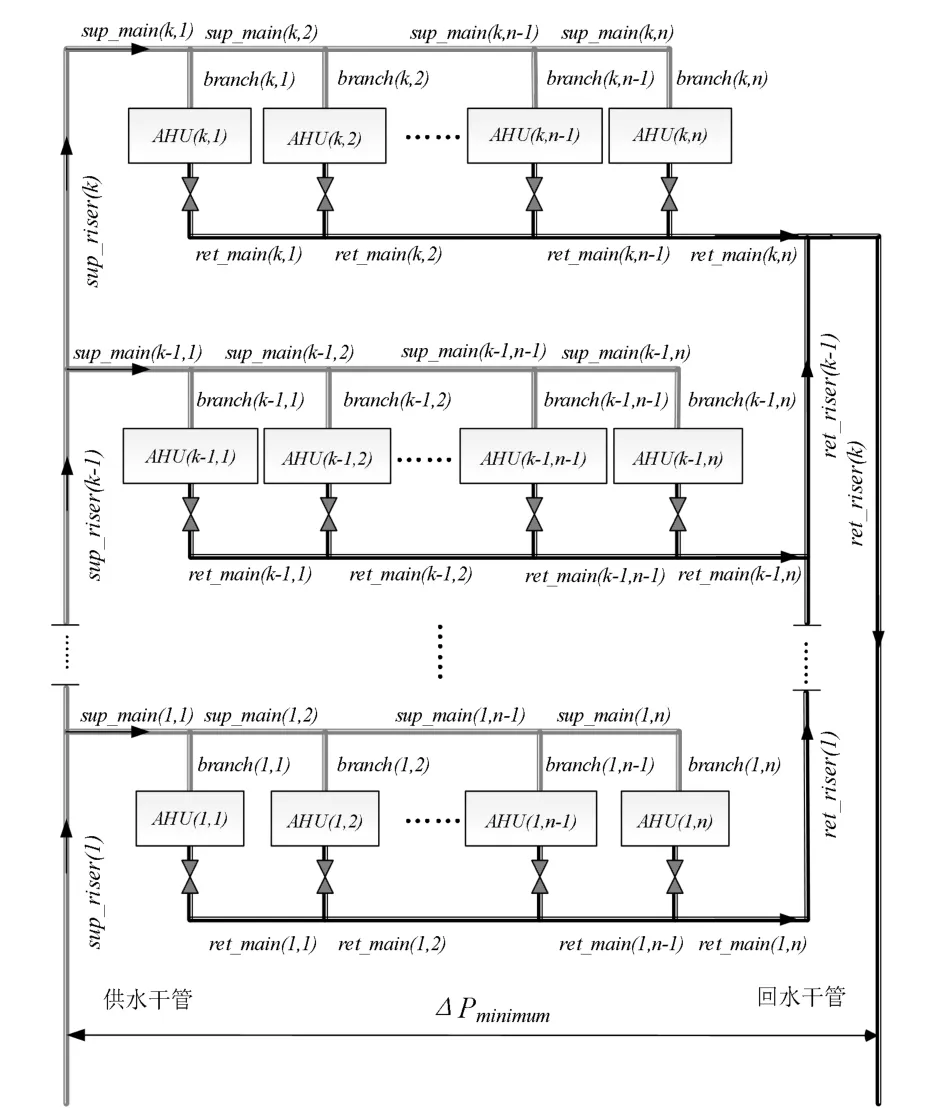
图1 同程管网的拓扑图模型Fig.1 T Topological Graph Model of Simultaneous Pipeline Network
1.1.2 末端换热设备热力模型
表面式换热器是最常见的空调系统末端换热设备,针对一次回风系统,在考虑传热传质以及能量守恒的情况下[11],室内外空气混合与表冷器送风处理室内热湿负荷的方程为:

在考虑热交换系数、接触系数与空气-水换热量平衡的情况下,表冷器处理空气过程方程为:

式中,iw、iN、ic、i0是室外、室内、风机盘管进风及出风的空气焓值,kJ/kg;dw、dN、dc、d0为室外、室内、风机盘管进风及出风的空气含湿量,g/m3;mnew为新风比;Q 为室内冷负荷,kW;W为室内湿负荷,kg/h;G 为表冷器风量,m3/h;Gbranch为表冷器水流量,kg/s;FAHU为表冷器换热面积选型,m2;tw1为冷冻水进水温度,℃;tw2为表冷器出水温度,℃。
由上述公式可知,在已知风机盘管类型、室内温度设置参数,室外空气状态参数、新风比、冷冻水进水温度的情况下,表冷器所需水流量Gbranch和表冷器出水温度tw2可表示为:
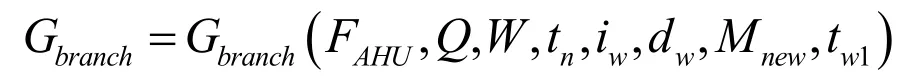
1.1.3 同程管网水力模型
管段内水流动的总压降包括沿程阻力压降和局部阻力压降,管段压降ΔP 可由公式(1)获得:
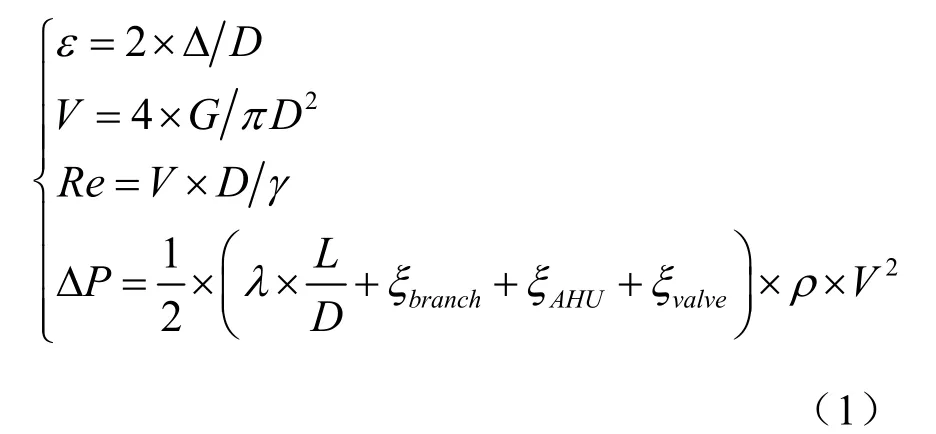
式中,ε为相对粗糙度;Re 为雷诺数;G 为管道流量,kg/s;D 为管径,m;Δ为表面粗糙度,m;γ为冷冻水的平均动力粘度,取值1.3×10-6;ξbranch为管道局部阻力系数;ξAHU为末端局部阻力系数;ξvalve为阀门局部阻力系数;L 为管道管长,m;λ 为管道沿程阻力系数。
假设末端支路的温控阀采用比例积分线性调节阀且可以对管网进行水力调节。根据并联环路压力平衡的原理,已知各管段压降的情况下,计算各支路中最大压降作为管网的最小供回水压差,由温控阀对其余管网支路的压降进行调节以达到压降平衡[12]。最小供回水压差ΔPminimum的计算公式(2)如下:
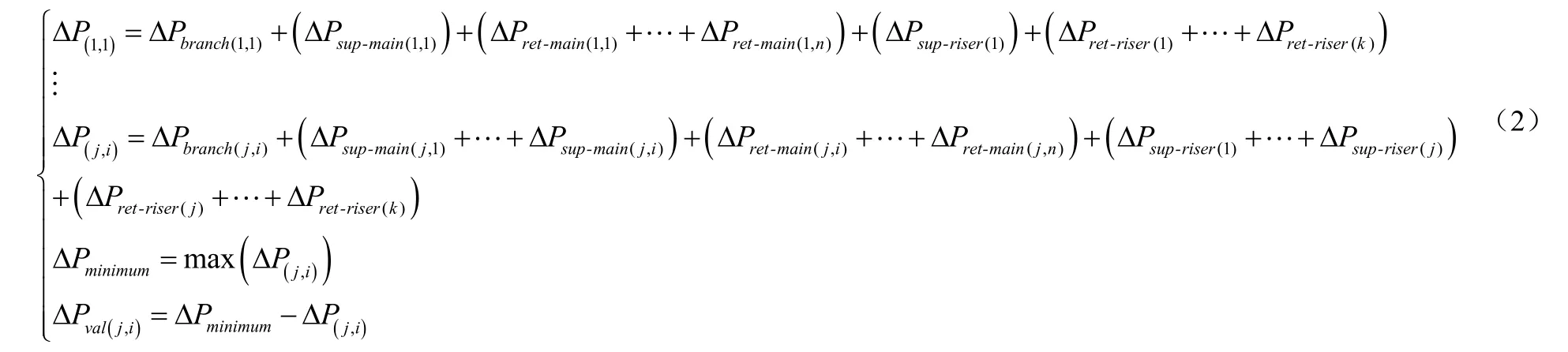
式中,ΔPbranch(j,i)为末端支路压降,Pa;ΔPsup_main(j,i)为供水干管压降,Pa;ΔPret_main(j,i)为回水干管压降,Pa;ΔPsup_riser(j)为供立管压降,Pa;ΔPret_riser(j)为回水立管压降,Pa,ΔP(j,i)为各支路总压差,Pa;ΔPminimum为最小供回水压差,Pa;ΔPval(j,i)为阀门损耗压降,Pa。
1.2 目标函数
中央空调系统经济性评价一般包括空调投资费用、空调年运行费用与系统的维护和折旧费用[9],在考虑上述费用的情况下,本文以能源利用效率为目标函数[13],能源利用效率的定义为输送到用户的能量与冷冻水系统消耗能量的比值,表达式为:
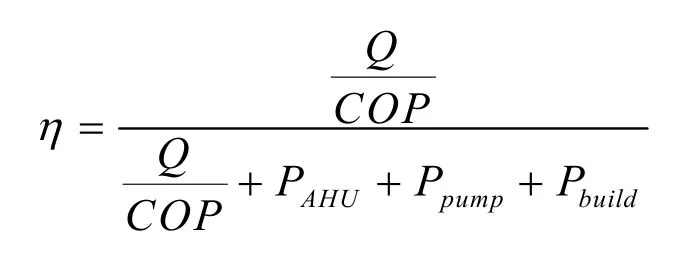
式中,Q 为制冷量,kW;COP 为能效比。
间接等效功率Pbuild为建筑设备投资维护费用 等价转化为建筑实际运行功率的数值,表示为:
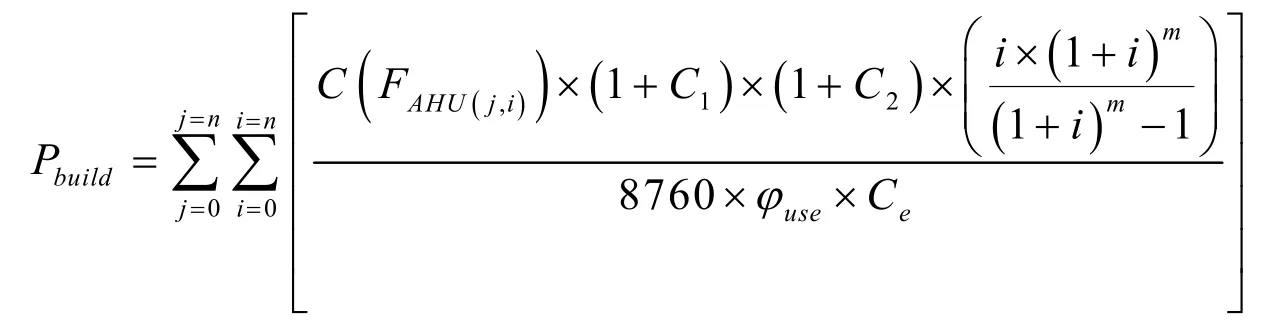
C 为表冷器的投资金额,元;C1为表冷器的安装成本系数;C2为表冷器的维护成本系数;实际贴现率ig为通货膨胀率;id为贴现率、m 为投资回收周期[10],年;φuse为表冷器的使用率、Ce为电价,kWh/元。
末端运行总功率PAHU为:

输送功率Ppump为:
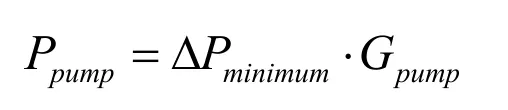
式中,ΔPminimum为输送冷冻水的最小供回水压差,Pa;Gpump为输送冷冻水的流量,kg/s。
1.3 近似优化计算方法
1.3.1 随机走步的近似优化算法
(1)局部最优计算过程
冷冻水系统末端优化设计的寻优自变量是末端的换热面积矩阵F=(f1,f2,……,fn),其中n为末端编号,优化目标为冷冻水系统能源利用效率η(F),设置随机走步的步长A,控制模量为M。为了消除不同变量之间的数量级差异,以最大最小值为上下限,将换热面积矩阵进行归一化处理,转化为-1~1 的数值。为避免陷入局部最优的情况,以末端换热面积选型的最大值和最小值为约束条件,将寻优自变量矩阵等距离划分为m 个寻优计算面域。
针对第m 个面域,以末端换热面积选型平均值作为每个计算面域的初始寻优中心,设置为F0=(f10,f20,……,fn0),获取一随机矩阵(a1,a2,……,an)T,an为一定范围内的随机变量。通过随机矩阵得到模为1 的随机单位向量Uk:
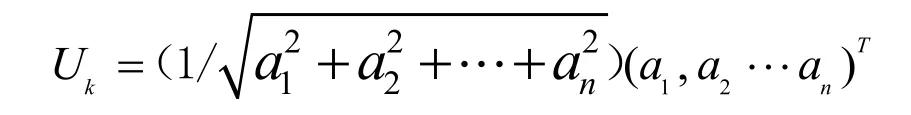
并根据换热面积选型的最大值、最小值及控制模量计算步长比例系数lamta:
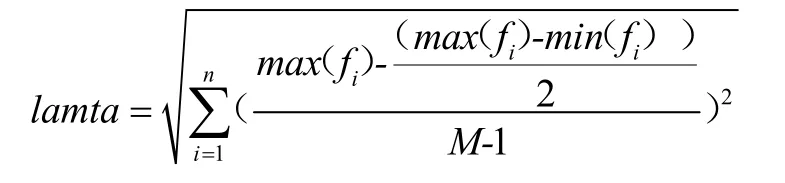
获取下一步随机矩阵Fk,其中fik=fi0+m·lamta·Uk(ai),对下一步随机矩阵进行逆归一化处理,并计算冷冻水系统能源利用效率η(F)k。若η(F)k>η(F)temp,则保存优化结果η(F)temp=η(F)k,Ftemp=Fk。保持寻优中心不变,取下一步随机矩阵继续计算η(F)k+1。直到步骤次数N 达到设定值,跳出迭代循环,继续下一个面域的寻优计算。
(2)全局最优计算过程
取上节m 个寻优计算面域中能源利用效率最高的面域所对应的自变量矩阵Fop作为全局优化的起始自变量,获取下一步随机矩阵Fk,其中,fik=fi0+A·lamta·Uk(ai),计算冷冻水管网能源利用效率η(F)k。若η(F)k>η(F)temp,则η(F)temp=η(F)k,对应的随机矩阵作为新的寻优中心F0=Fk,否则取下一步随机矩阵继续计算η(F)k+1。当步骤次数达到设定值时,减小步长A,并根据步长A 对步骤次数N进行调整,以减少循环迭代的次数,提高计算效率。若A<ε,迭代完成,得到末端的换热面积矩阵最优解Fop和ηop[14]。
1.3.2 表冷器结构参数连续化
在寻优计算过程中,为保证近似优化算法的准确性与收敛性,本文以表冷器的换热面积FAHU作为其型号标识,即每一种换热面积代表一种表冷器选型规格,将离散的表冷器选型连续化。其余结构参数,包括表冷器的迎风面积Fy,风量G,功率PAHU,价格CAHU,水侧局部阻力系数ξAHU等,可由表冷器换热面积拟合而成,实现降维处理。拟合函数(3)如下所示:
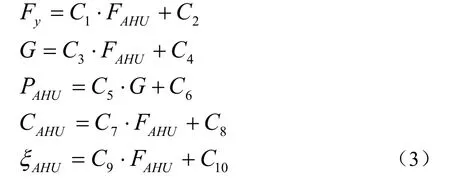
式中,C1、C2、C3、C4、C5、C6、C7、C8、C9、C10为拟合函数的经验参数,可由实际数据拟合获取。
1.3.3 次优理论分析及次优解群获取
对于多变量优化问题,变量组合方式多样,由于计算效率的限制及数据的稀疏性,通过近似算法只能对部分组合进行计算,其优化结果不一定是最优解。其次,当负荷发生波动或者是建筑功能改变的情况下,末端选型最优解不一定适应实际工况,其能源利用效率也不一定是最高。所以必须使用次优理论的方法来处理多变量优化问题,以寻求对不同负荷工况具有适应性的末端选型。
本文引入能源利用效率裕度作这一指标来获取次优解群Gsub,其中能源利用效率裕度表示为次优解群中最大值和最小值之差与次优解群最大值的比值,其中次优解群的最大值一般是优化解群的最大值,可表示为:
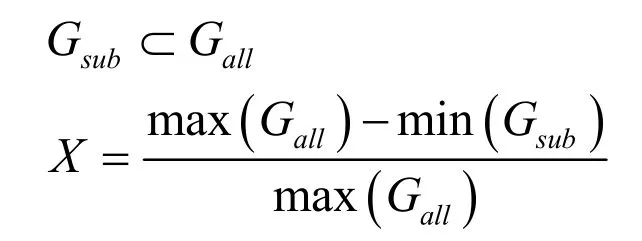
式中,Gsub为次优解群,Gall为算法迭代计算输出的总优化解群,X 为此优化结果的能源利用效率裕度。本文以能源利用效率裕度2%的数据集作为次优解群。
对于末端优化问题,不同末端的选型的概率是独立的 , 满足独立性假说 , 由P(f1|Gsub)max·P(f2|Gsub)max·……·P(fn|Gsub)max=P(f1,f2,……,fn|Gsub)max可知,假如已知次优解群Gsub中(f1,f2,……,fn)的最大概率选型,那么(f1,f2,……,fn)同时发生的能源利用效率η(f1,f2,……,fn)也是最大的。通过上述分析可得,以次优解群中概率密度最大的区域作为优化的次优解,可以使末端选型在一定的负荷变化下仍有较高的能源利用效率。
1.4 冷冻水系统空调末端优化计算过程
获取建筑的房间数量,管道的长度以及管径等结构参数,及建筑房间的热湿负荷,温度设定值,室外干湿球温度,冷冻水系统供水温度,新风比等负荷参数。以末端换热面积选型平均值作为初始优化中心,计算其能源利用效率。通过随机走步变步长的近似优化算法不断对末端选型进行迭代优化,得到优化结果,输出次优解群,并对次优解群进行统计分析,优化过程如图2 所示。

图2 优化路径Fig.2 Optimized Path
2 计算结果及讨论
2.1 结构参数设置
表1 为表冷器换热面积与其他结构参数关联式的经验参数值。由实际数据拟合而成。

表1 拟合函数的经验参数表Table 1 The empirical parameter table of fitting function
管径按照推荐流速法选取。供水干管Lsup_main与回水干管Lret_main为7 m,末端支路Lbranch的管长、供水立管Lsup_riser,回水立管Lret_riser的管长为5 m。管道局部阻力ξbranch为3,温控阀全开的局部阻力ξvalve为22,温控阀管径为DN20。
2.2 建筑负荷参数设置
为了探究随机走步变步长的近似优化方法对末端选型的优化效果,本文构建5 层规模的建筑模型,每层设置50 个末端(编号为S5_50),设置5种随机负荷分布和1 种平均负荷分布工况,分别命名为T_1、T_2、T_3、T_4、T_5、T_6。为了研究建筑规模对优化算法的影响,针对随机的负荷工况,本文再构建10 层、15 层、20 层的建筑模型,每层50 个末端(编号分别为S10_50、S15_50、S20_50),各工况负荷分布如图3 所示。
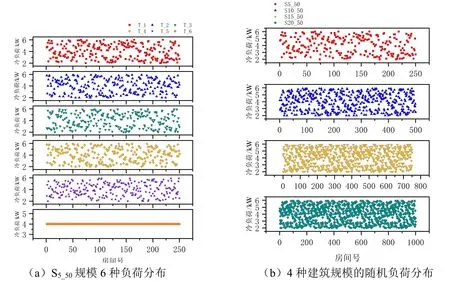
图3 各负荷分布的负荷取值Fig.3 Load value of each load distribution
在进行末端设计时,室内干球温度取25℃,室内相对湿度维持在40%~65%之间,室外干球温度取33.5℃,室外湿球温度取27.7℃,新风比取0.1,冷冻水进水温度取7.0℃,末端平均冷负荷均为4kW,湿负荷为0.55g/s。通货膨胀率取8%、贴现率取4%[10]、回收周期取15年、使用率取0.75、电费取0.69 元/kWh、能效比取5。
2.3 近似优化算法优化结果
2.3.1 迭代过程
为了验证随机走步变步长的近似算法对末端优化问题的有效性,以S5-50规模6 种负荷分布为例,通过随机走步变步长的近似优化算法,对中央空调能源利用效率模型进行多变量优化求解。
图4 反映了使用随机走步变步长的算法对S5_50规模T_6 工况多次进行优化计算的迭代过程。由图可知,在迭代初始的时候,不同优化次数的能源利用效率较低,不到0.800,随着迭代次数的增加,中央空调系统的能源利用效率都急速增加,当迭代次数超过200 次后,能源利用效率达到0.844~0.855,提升的速度放缓,最终达到一个极值并跳出循环,多次优化结果的能源利用效率集中在0.878~0.882,不同优化次数的优化结果相差不到0.004,可得,在算法初始寻优中心不同的情况下,算法仍有较高的收敛性与稳定性,随机走步变步长算法对初始自变量的选择不敏感,且复现性较好。
2.3.2 能源利用效率优化结果分析
能源利用效率最高点仅代表通过近似优化得到的最优结果,当负荷偏离设计工况时,不一定满足最高能源利用效率的要求,而其中次优解中概率密度最大的能源利用效率虽然小于最优解,但是其末端选型的范围最广,对不同负荷的适用性最好,故本文以概率密度最大的次优解作为近似优化的解,次优解群的获取由1.3.3 节与图4 可得。
在设计负荷条件下,以表冷器进出水温差为5℃且进水温度为7℃时所对应的换热面积作为传统设计的换热面积选型。
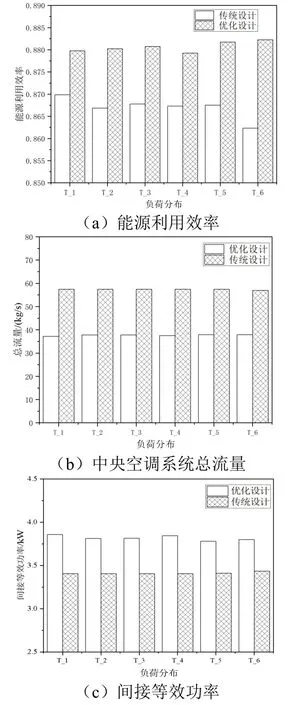
图5 反映了S5_50规模6 种负荷分布优化前后中央空调系统各参数的变化情况。由图可知,随机走步变步长的近似优化算法对不同负荷工况均有优化效果,6 种负荷工况的平均能源利用效率从0.867 上升到0.881,增加了0.014。由图也可知优化后的总供水流量以及系统最小供回水压差均有下降,6 种负荷工况的平均流量从57.3kg/s 下降到36.7kg/s,最小供回水压差从220kPa 下降到90kPa。而优化后系统的间接等效功率略有上升,间接等效功率从3.4kW 提高到3.8kW。说明通过优化算法,可以适度提高末端选型,有效降低系统的流量与最小供回水压差,进而提高系统的能源利用效率。

图5 中央空调系统能源利用效率及其他参数的优化结果Fig.5 Optimization results of energy utilization efficiency and other parameters of central air conditioning system
2.3.3 换热面积选型优化结果分析
图6 反映了S5_50规模6 种负荷分布次优解集的末端换热面积选型与传统选型末端选型,对图6的6 种负荷工况次优解集的换热面积概率密度进行统计,可得图7。由图可知,6 种负荷工况优化设计的末端选型随负荷的波动而变化,优化后末端选型可以对负荷进行精确响应。且优化后末端的选型相较于优化前有较大的提升,6 种负荷分布平均末端换热面积选型从6.68m2提高到8.05m2,增加了21%,证明了算法的有效性。
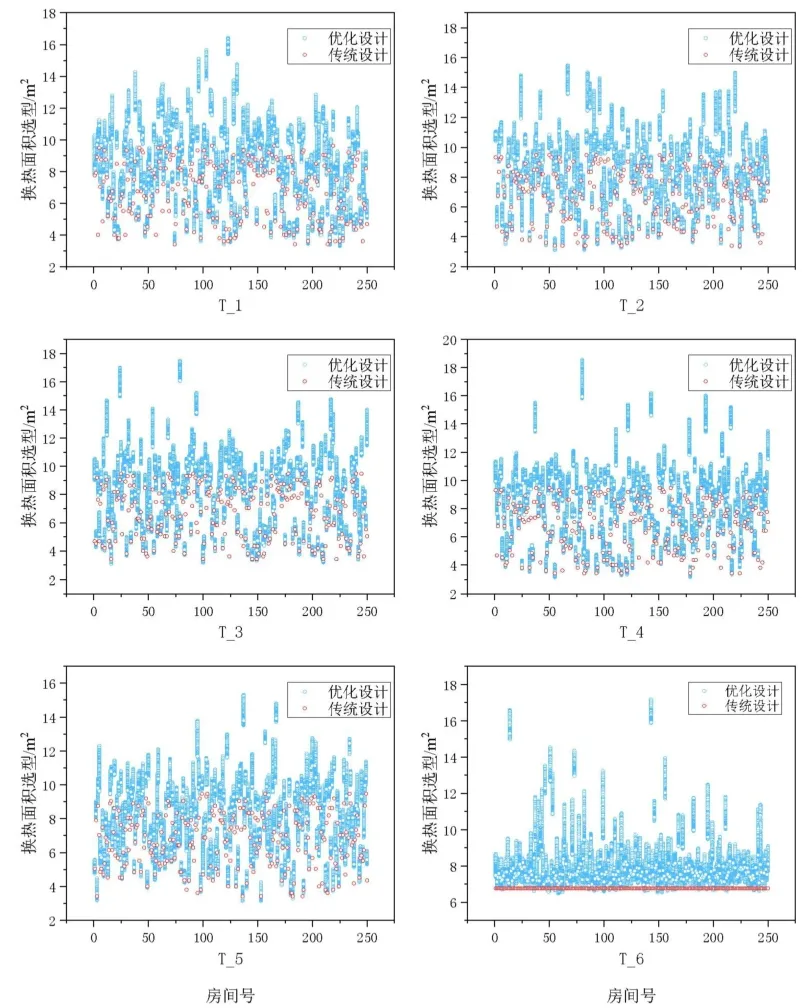
图6 末端换热面积选型的优化结果Fig.6 Optimization results of terminal heat transfer area selection
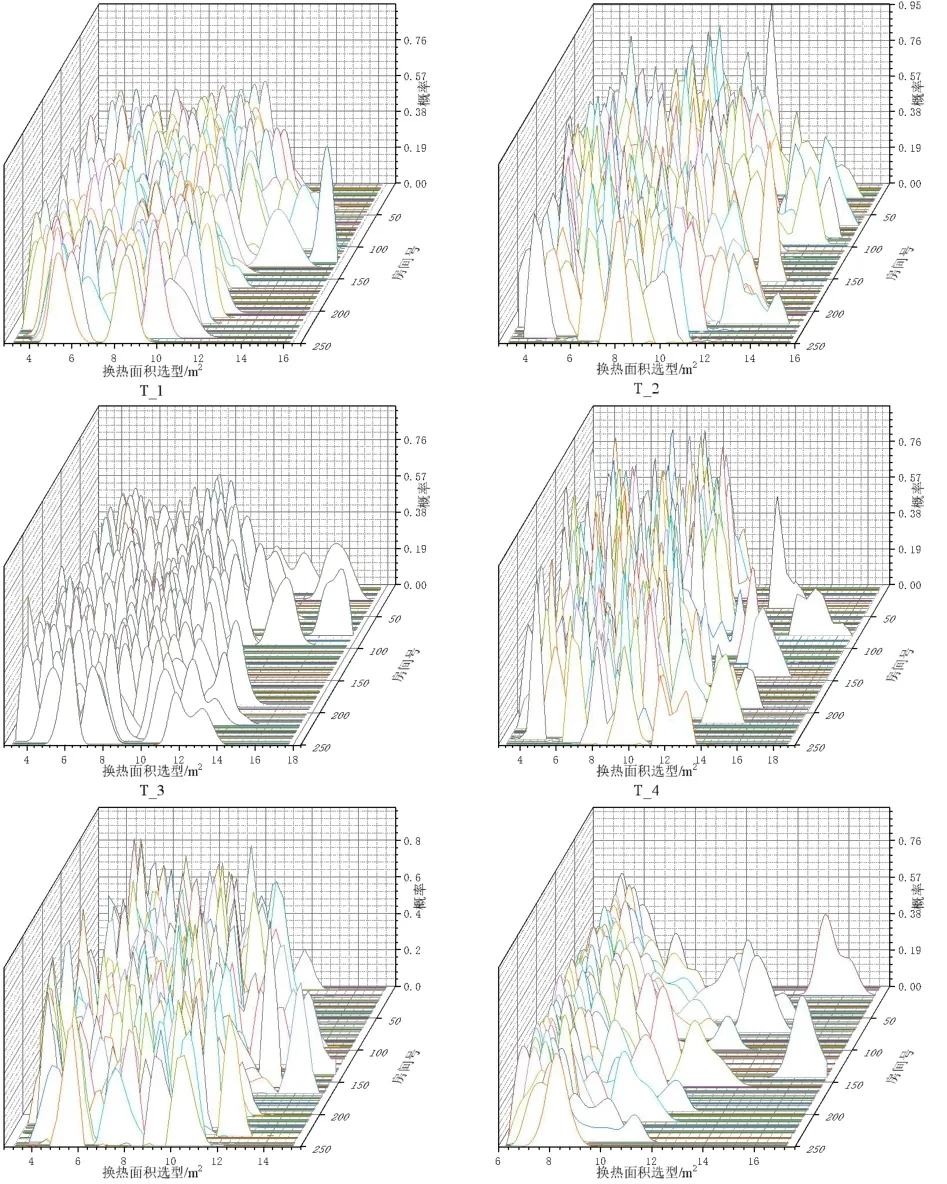
图7 末端换热面积选型概率密度Fig.7 Probability Density of Heat Transfer Area Selection for Air Conditioning Terminal
2.4 建筑规模对近似优化算法的影响
图8 反映了不同建筑规模优化前后的能源利用效率。由图可知,优化后5 层建筑规模最大概率的能源利用效率从0.867 提高到0.879,增加了0.012。而20 层建筑规模最大概率的能源效率从0.843 提高到0.845,仅增加0.002。可得随着建筑规模的增加,随机走步变步长算法优化的效果不断下降。原因在于本优化算法采用随机组合的方式对自变量进行寻优,当自变量数目较多时,寻优组合方式成倍增加,由于数据的稀疏性及计算效率的限制,很难在随机的组合集中找到最优的组合。
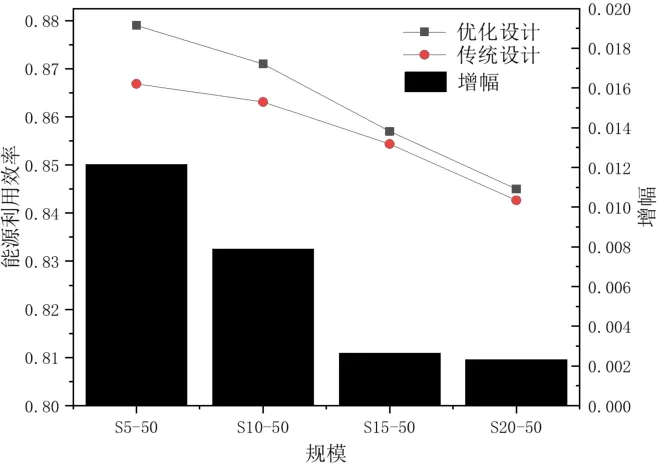
图8 4 种建筑规模能源利用效率概率的优化结果Fig.8 Optimization results of four building-scale energy efficiency probabilities
2.5 随机负荷取值范围对近似算法的影响
由上文可知对某一特定的负荷分布形式,随机走步变步长近似优化算法与传统设计相比能源利用效率均有一定的优化效果。但在实际运行过程中,末端处理的热湿负荷在不断变化,末端设计选型过程中随机性比较大,提高末端对不确定负荷的适应性对中央空调系统的高效运行至关重要。
对S5_50规模T_1 负荷分布进行随机取值,随机取值方法为,在以设计负荷为基准的上下5%、15%、25%的负荷区间内随机取值,每种负荷区间取10 种随机负荷工况,随机负荷取值如图9 所示。对图9 的10 种随机负荷进行优化计算,将各种随机负荷工况计算的次优解群作为同组数据进行统计分析,获得适应不同负荷工况的末端换热面积选型的概率分布。
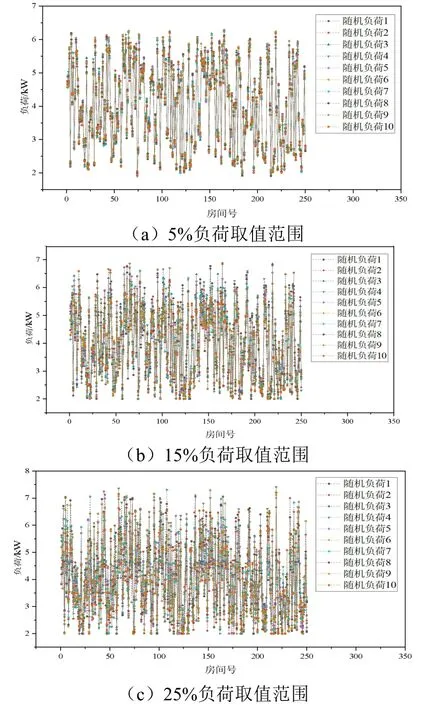
图9 不同负荷取值范围的10 种随机负荷取值Fig.9 10 random load values with different load fluctuations
图10 反映了优化后3 种负荷取值范围的次优解群中换热面积选型的概率分布。由图可知优化后换热面积选型趋势与负荷分布的趋势基本吻合,优化算法可以根据负荷的分布情况匹配相应末端选型,侧面验证优化算法的有效性,且随着负荷波动的加剧,同一房间的换热面积选型的上下限也越大,概率分布也越平均。
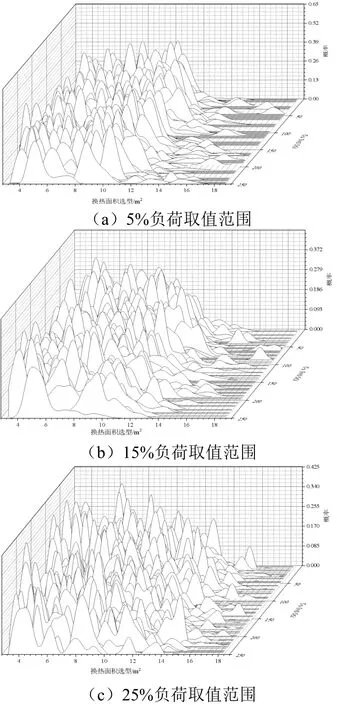
图10 各房间次优解群换热面积选型的概率分布Fig.10 Selection probability of heat exchange area of each room
2.6 反向验证
2.6.1 反向验证过程
取随机负荷次优解群的概率分布中概率密度最大的区域作为末端选型优化问题的次优解。图11 反映了S5_50规模T_1 负荷分布第10 个房间的选型取值区间。如图所示,为了探求选型随机性对中央空调系统能源利用效率的影响,以及对近似优化算法的次优解进行反向验证,本文以次优解中概率最大的选型换热面积的(90%~110%)选型区间为次优解的选型区间。

图11 反向验证末端取值范围Fig.11 Reverse verification end value range
在寻优计算过程中,空调末端选型作为优化计算模型的输入变量,在寻优计算过程中是连续变化的,以保证算法的准确性与收敛性。但优化计算所得的末端选型不可以直接应用于实际工程项目中,而是先将选型转化为实际末端换热面积选型,再进行计算,实际末端取值如表2 所示。

表2 实际表冷器选型与换热面积的对应关系Table 2 The corresponding relationship between actual surface cooler selection and heat exchange area
图12 反映了S5_50规模T_1 工况第一层第10个房间的换热面积选型概率分布。由图可知,一个末端有多种实际选型取值结果,将优化后连续的末端取值转化为实际末端取值时,应选取最靠近次优解的实际末端选型取值。
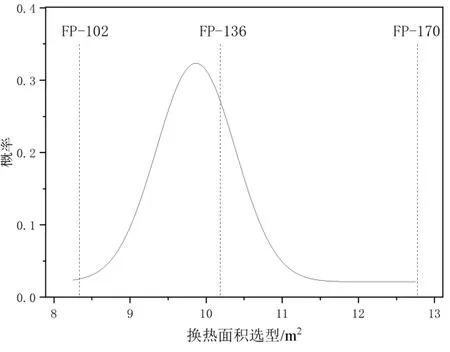
图12 离散末端取值概率Fig.12 Discrete terminal probability
在考虑末端选型的随机性的情况下,对不同负荷工况次优解的随机选型区间进行随机取值,得到中央空调系统末端选型,并计算在该负荷分布条件下的能源利用效率,将计算结果输出到解集进行统计分析。
2.6.2 6种负荷分布反向验证
图13 反映了6 种负荷分布反向验证实际换热面积选型取值。由图可知,优化设计整体选型大于传统选型,传统设计的换热面积选型为7.01m2,而优化设计的换热面积选型为8.22m2,增加了17.3%。
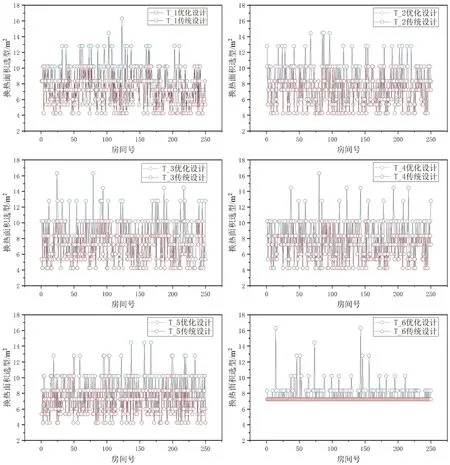
图13 6 种负荷分布反向验证换热面积选型取值Fig.13 Six load distributions reverse verification of heat transfer area selection values
图14 反映了6 种负荷分布反向验证的能源利用效率。由图可知,优化后T_1 到T_5 负荷工况实际平均能源利用效率从传统设计的0.870 提升到0.875,而T_6 负荷工况优化后实际能源利用效率从传统设计的0.885 降低到0.880。原因在于数据的稀疏性导致反向验证存在统计学偏差,但是偏差在5%的范围内,属于合理的置信区间。
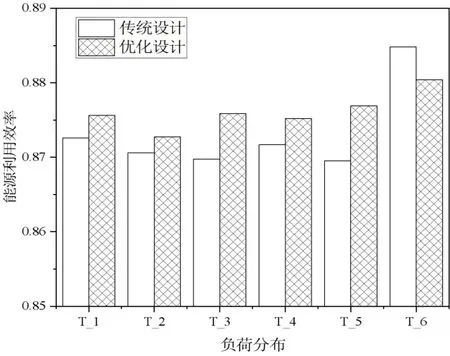
图14 反向验证能源利用效率Fig.14 Reverse verification of actual energy efficiency
2.6.3 3 种负荷随机取值范围反向验证
图15 反映了S5_50规模T_1 工况第一层50 个末端反向验证实际换热面积选型的取值。由图可知,优化设计的实际面积取值虽与传统设计有重叠,但是优化设计整体选型大于传统选型,其中传统选型的末端平均换热面积选型仅为6.960m2,而负荷波动为25%的末端平均换热面积为7.750m2,增加了11.3%。说明通过次优方法,在考虑负荷波动的情况下,会适度提高末端的选型大小,以提高对负荷的适应性。
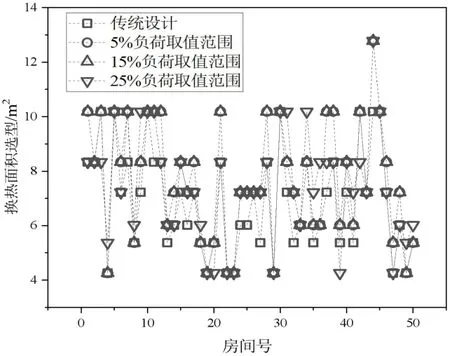
图15 反向验证换热面积选型取值Fig.15 Reverse verification of heat exchange area selection value
图16 反映了S5_50规模T_1 工况3 种负荷取值范围对10 种随机负荷工况反向验证的能源利用效率解集正态分布。表3 反映了3 种负荷取值范围反向验证能源利用效率解集正态分布的参数。由图和表可知,随着负荷取值范围的增加,优化设计与传统设计的能源利用效率均不断减少,优化设计的能源利用效率均值从5%负荷取值范围的0.878 降低到25%负荷取值范围的0.783,减少了10.8%。但是优化设计相较与传统设计能源利用效率仍有较大的提升,随着负荷波动的增加,优化后能源利用效率增量从5%负荷取值范围的0.015 提高到25%负荷取值范围的0.087。由图和表也可知,随着负荷波动的增加,反向验证能源利用效率的范围也不断增加,其中优化设计的95%置信区间的上下限之差从5%负荷取值范围的0.010 提高到25%负荷取值范围的0.061,且优化后95%置信区间的下限比传统设计95%置信区间的上限高0.04,说明负荷的波动会使末端偏离其设计工况,导致能源利用效率的降低,并增加能源利用效率的波动范围,不利于系统的节能运行。但是通过考虑负荷的不确定性,对末端进行多次优化寻求适用性较强的次优解,可以提高中央空调系统的节能效果以及对随机的负荷分布的适应性。

表3 反向验证能源利用效率解集正态分布参数Table 3 Verify the normal distribution parameters of the energy use efficiency solution set reversely
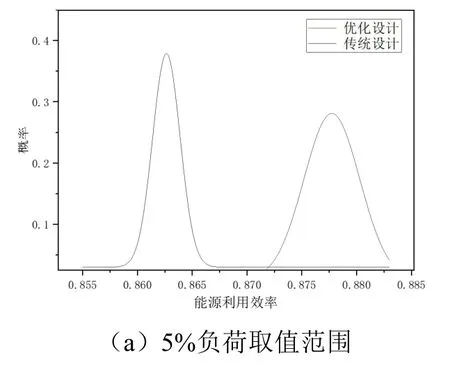
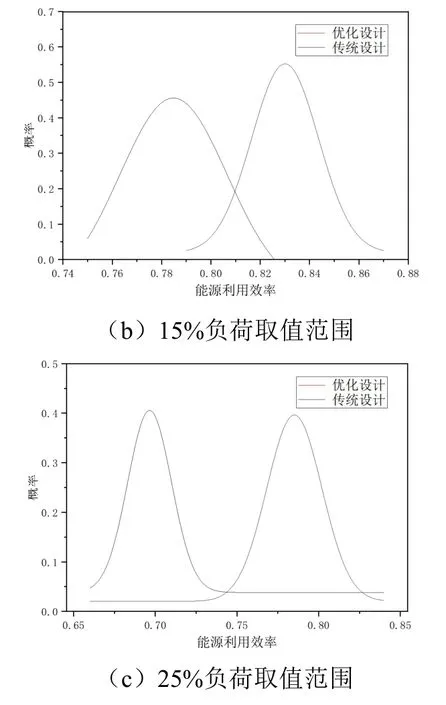
图16 实际验证能源利用效率解集正态分布Fig.16 Energy use efficiency reverse verification solution set normal distribution
3 结论
由于实际中央空调系统具有多变量非线性高度耦合的特性,且中央空调系统运行过程中负荷具有随机性,传统优化算法很难对末端选型进行优化。为此,本文使用随机走步变步长的近似优化算法,在考虑负荷随机波动的条件下,通过对次优解群进行统计分析,探索末端选型设计的优化方法,得到以下结论:
(1)随机走步变步长的近似优化算法对不同的负荷工况均有一定的优化效果,平均其能源利用效率可增加0.014。不同优化次数的优化结果相差不到0.004,算法的收敛性与稳定性较好,可复现性较高。优化后的换热面积选型与负荷分布的趋势基本吻合,验证了算法的有效性。取次优解群中概率密度最大的区域作为末端选型优化问题的次优解,对其进行反向验证,反向验证的平均能源利用效率相较传统设计方案仍有较大的提高。
(2)对于多变量优化问题,由于计算效率的限制,对于某些负荷工况很难在随机的组合集中找到最优的实际离散末端选型组合,特别是针对20层建筑的负荷工况,其能源利用效率的增量仅仅达到0.002。
(3)随着负荷取值范围的增加,优化设计与传统设计的能源利用效率均不断减少,优化设计降幅可达10.8%。但是优化设计的能源利用效率相较与传统设计仍有较大的提升,增量可达0.087,且优化后95%置信区间的下限比传统设计95%置信区间的上限高0.04,说明负荷的波动会使末端偏离其设计工况,导致能源利用效率的降低,并增加能源利用效率的波动范围。但是通过次优理论,可以提高中央空调系统的能源利用效率以及对随机的负荷分布的适应性,对末端的选型优化有重要指导作用。
