应用改进人工蜂群算法的VCRU冷凝温度PIλDμ控制的数值研究
2022-09-20李东升李绍勇阴志杰
李东升 李绍勇 阴志杰
(兰州理工大学土木工程学院 兰州 730050)
0 引言
如今中央空调系统(Central Air Conditioning System,CACS)在建筑领域中的应用越加广泛[1],而作为CACS 冷、热源子系统中的重要设备-蒸汽压缩式制冷机组(Vapor Compression Refrigerating Unit,VCRU),具有结构简单,便于操作,输出冷、热负荷大和能效比(Coefficient of Performance,COP)高等特点[2],CACS 功能的发挥与其运行工况密切相关。其中作为VCRU 关键部件之一的冷凝器,担负着将在空调房间室内吸收到的热量通过它释放到室外环境的重要作用[3],其冷凝效果可通过重要参数—冷凝温度Tc来表征。而Tc测量值是否满足制冷循环工艺所要求的设定值Tc,set,对于实际运行的冷凝器及其VCRU 至关重要。文献[4]研究了Tc,set变化对于VCRU 运行能耗的影响,结果表明:当Tc,set=40℃~45℃和45℃~50℃时,压缩机运行能耗可分别提高13%和8%。文献[5]指出在蒸发温度不变的情况下,Tc平均值每下降1℃,VCRU的COP 值可相应地提高3.76%。由此可见,设计适当的冷凝温度控制系统,确保Tc=Tc,set,使得冷凝器及其VCRU 安全、经济运行,已成为国内外空调制冷技术领域的研究热点之一[6]。
针对冷凝温度控制这一问题,Lee 等[7]提出了一种冷却水回水温度设定值固定的方法,该方法能够实现Tc=Tc,set效果,同时可消除由于室外湿球温度变化,使得冷却水供水温度也发生变化,对Tc的影响。Li 等[8]提出了一种在CO2跨临界制冷系统中增加经济器的方法,该方法可以有效降低冷凝器出口的冷凝温度Tc,且COP 值也得到一定提升。Al-Bassam 等[9]提出了一种根据冷凝温度变化,变速调节冷却塔风机转速的方法,结果表明:在不同冷负荷需求和不同环境湿球温度下,该方法可保持稳定的冷却塔出水温度并可以有效调节Tc。吴斌[10]提出了一种流经冷凝器的冷却水供、回水温差的控制方法,该方法可快速反映冷凝温度的变化,同时确保Tc=Tc,set。张瑞等[11]提到了一种流经冷凝器的冷却水供、回水压差ΔP 的控制方法,该方法可有效地避免Tc波动过大对VCRU 稳定运行产生的影响。王磊等[12]提出了一种利用回热器增加回热循环的方法,结果表明:该方法可以通过改变冷凝器出口的过冷度,达到控制Tc的效果。
PID 控制方式以其结构简单、鲁棒性强、可靠性高和便于理解与操作,在暖通空调、制冷等实际系统或工程中得到普遍应用[13]。对于PID 控制的核心问题-控制器参数整定,文献[14]提出一种基于遗传算法优化神经网络连接权值和阈值的方法,来整定PID 控制器参数。结果表明:该算法可为神经网络提供最优连接权值和阈值,进一步缩短PID控制器参数的整定时间,同时PID 控制系统在瞬态、稳态和鲁棒性能方面都得到很大提升。基于人工蜂群算法,文献[15]设计了一种精英学习策略,从而求解PID 控制器参数的优化问题。采用环形拓扑结构和遗传算法的交叉、变异、选择操作,产生精英个体,再优化PID 控制器参数。结果表明:采用该策略可以有效提高算法的搜索能力和开发能力,整定出PID 控制器参数的最优值,系统的控制品质也得到进一步的提高。
相比PID 控制器,由于PIλDμ控制器中加入了积分算子阶次λ和微分算子阶次μ,扩大了控制区间并提升了控制效果[16],但增加了PIλDμ控制器参数整定的难度与计算负荷。文献[17]提出一种采用改进粒子群算法整定PIλDμ控制器参数的方法。先根据多因素、多水平试验,得到粒子群算法的最优基本参数,再对PIλDμ控制器参数进行离线优化。对比参数整定的仿真结果,表明该方法收敛速度更快,且PIλDμ闭环控制系统的阶跃响应在超调量、上升速度和调节时间,均比普通PID 控制方式更好。文献[18]提出一种基于随机进化灰狼算法的PIλDμ控制器参数整定方法。对种群的更新过程采用可变的进化速率来描述,从而增强更新过程的随机性和收敛速度,再对PIλDμ控制器参数进行在线自整定。结果表明:算法精度和收敛速度有效提升,且设计的PIλDμ控制器能明显改善系统的抗干扰能力,系统的鲁棒性相比普通PID 控制系统也得到增强。
综上和考虑密切Tc的冷凝器被控对象存在结构参数时变、大惯性和时滞等特点,本文提出VCRU 冷凝温度PIλDμ控制系统(Fractional Order PID Control System,FOPIDCS)的设计方案,即在冷凝器低温高压液态制冷剂的出口端设置冷凝温度测量变送器,实时测量冷凝温度Tc并上传给冷凝温度PIλDμ控制器,求偏差ΔTc=Tc,set-Tc 和对ΔTc进行PIλDμ运算后,输出控制指令p 给冷却水流量电动调节阀。改变其开度,使得流经冷凝器的冷却水流量qcw发生变化,从而保证Tc,set=Tc,实现冷凝器的安全、经济运行。此外,依据基本人工蜂群算法( Basic Artificial Bee Colony Algorithm,BABCA),对学习因子c1和c2进行线性变化,同时保持其他参数不变,重构改进人工蜂群算法( Improved Artificial Bee Colony Algorithm,IABCA)和选择min ITAE(Integrated Time Absolute Error, 绝对积分时间误差)作为其目标函数。运用该IABCA 对冷凝温度分数阶PID 控制器(Fractional Order PID Controller for Condensation Temperature,CT-FOPIDC)参数进行优化整定,获取对应的最佳值。仿真结果表明,该冷凝温度FOPIDCS 和IABCA 是 可行 的, 能 求解 出CT-FOPIDC 的5 个参数最佳值,且Tc的调节品质得到明显提升。
1 VCRU 中的冷凝温度控制
1.1 单级制冷循环工艺中的冷凝温度测控
对于VCRU 单级制冷循环工艺而言,一般是通过调节冷却水流量qcw来控制冷凝温度Tc[7],冷却水的进/出口温度为32℃/37℃,相应的测控流程图如图1 所示。
图1所示是一个VCRU单级制冷循环工艺:在蒸发器中吸收空调冷冻循环水的热量后,低温低压液态制冷剂由蒸发器排出,而被压缩机吸入。再经过压缩机的做功,使其变成高温高压的制冷剂蒸汽后,进入冷凝器。在此与来自冷却塔的冷却水进行热量交换,而被冷凝为低温高压的液态制冷剂。通过热力膨胀阀节流与降压后,变成低温低压的液态制冷剂进入蒸发器。再次吸收空调循环冷冻水的热量,又成为低温低压的制冷剂蒸汽。这样完成压缩、冷凝、节流和蒸发四个热力过程的循环,实现VCRU的制冷目的[19]。

图1 VCRU 单级制冷循环工艺测控流程图Fig.1 Flow chart of measurement and control for VCRU with one stage refrigeration circulating process
当VCRU 中蒸发器侧的冷负荷需求发生变化时,相应进入冷凝器的高温高压的制冷剂蒸汽流量也会发生变化,则Tc也随之变化,导致Tc偏离Tc,set,即Δ Tc=Tc,set-Tc≠0。此时TT 将测得的冷凝器出口端低温高压制冷剂温度,近似反映Tc大小的标准电流信号传递给TC,进行求偏差Δ Tc。再对Δ Tc进行相应的PIλDμ运算后,输出控制指令p 给冷却水流量电动调节阀(安装在冷凝器的冷却水入口端,水温32℃),改变其开度,导致进入冷凝器的冷却水流量qcw发生相应的改变,从而保证Tc=Tc,set,达到控制冷凝温度的效果。而且,当蒸发器侧的冷负荷发生扰动,流经冷凝器的冷却水流量qcw可快速响应,避免Tc产生较大波动,使得冷凝器安全、经济运行。
1.2 冷凝温度PIλDμ控制系统
(1)冷凝器温度被控对象的输入/输出特性
在VCRU 制冷系统中,冷凝器是一种常见的换热器形式,可视为一阶惯性加时滞环节,输入信号为冷却水流量qcw,输出信号为冷凝器出口端的冷凝温度Tc,传递函数如式(1)[20]。

式中,K 为冷凝温度调节通道的放大系数,%;τ为冷凝温度调节通道的滞后时间,s;T 为冷凝温度调节通道的时间常数,s。
(2)冷却水流量电动调节阀的输入/输出特性
它接受冷凝温度PIλDμ控制器输出的控制指令p(0~10mA·DC 或4~20mA·DC),通过改变阀门开度来控制qcw大小。本文选择对数流量特性的调节阀[21],传递函数如式(2)。

(3)冷凝温度测量变送器的输入/输出特性
它是将Tc转换为标准电流信号0~10mA·DC或4~20mA·DC 的设备,作用在冷凝温度PIλDμ控制系统的反馈通道上,实时测量Tc的大小,可视为比例环节[22],传递函数如式(3)。

(4)冷凝温度PIλDμ控制器的输入/输出特性
本文中的冷凝温度FOPIDCS 采用的是分数阶PID 控制器,其保留了整数阶PID 控制器结构简单、适应性好、鲁棒性强的特点,并且控制区间更广,控制效果更好,传递函数如式(4)[17]。

式中,KP、KI、KD、λ、μ为冷凝温度PIλDμ控制器的比例系数、积分系数、微分系数、积分阶次和微分阶次。
1.3 冷凝温度PIλDμ控制系统的构建
至此,本文拟研究的基于IABCA 冷凝温度PIλDμ控制系统,如图2 所示。
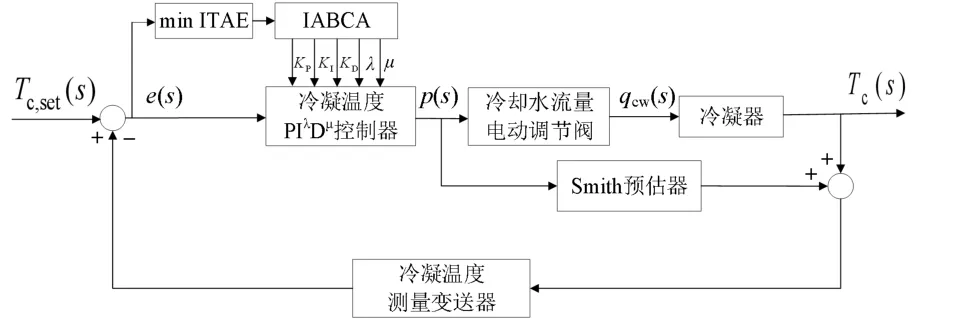
图2 基于IABCA 的冷凝温度PIλDμ控制系统方框图Fig.2 Block diagram of condensation temperature PIλDμ control system based on IABCA
分析图2,冷凝温度测量变送器实时测量冷凝温度Tc,并将其与Tc,set比较,求出e=Tc,set-Tc,继而通过IABCA 整定出冷凝温度PIλDμ控制器的5个参数[KP,KI,KD,λ,μ]。同时冷凝温度PIλDμ控制器输出控制信号p,控制冷却水流量电动调节阀开度,进而控制qcw的大小,确保Tc=Tc,set和冷凝器的安全、经济运行。此外,考虑到冷凝器温度的被控对象具有时延特性,在本文的冷凝温度PIλDμ控制系统中引入Smith 预估器[23],将滞后环节转移到闭环控制回路之外,消除对系统的不利影响,从而进一步提升系统的控制品质。
2 改进人工蜂群算法及其PIλDμ控制器参数的整定
2.1 改进人工蜂群算法
人工蜂群算法是一种受蜂群觅食行为启发而提出的算法,具有良好的全局搜索能力,受初始种群规模的影响较小[15]。在基本人工蜂群算法BABCA 中,包括引领蜂、跟随蜂、侦查蜂,在搜寻过程中,若一个解经过L 次循环都未得到更新,则认为该解陷入局部最优并被舍弃,该解对应的引领蜂转化为侦查蜂。每个蜜源代表搜索空间中的一个可行解。在蜂群搜索过程中,每个引领蜂会发现一个新蜜源,即对应一个新的可行解,搜索公式如式(5)所示[24]。
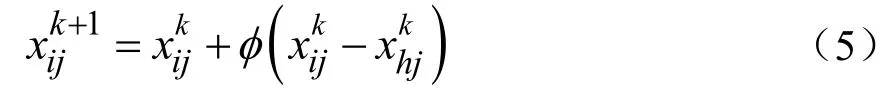
式中,i=1,2,…,N,h=1,2,…,N,N 为蜜源数量,h 不等于i;j=1,2,…,D,D 为求解问题的维度;φ为[-1,1]之间的随机数;为当前蜜源位置;为迭代后蜜源位置;k 为当前迭代次数。
为了提高BABCA 的全局搜索能力和局部搜索能力,同时期望引领蜂搜寻到的新蜜源都是好蜜源。鉴于此,本节引入文献[25]中的代表当前搜寻到的最佳位置bpij,此位置称为个体极值点pbest,以及搜寻到的全局最佳位置bgij,此位置称为全局极值点gbest,并提出线性变化的学习因子c1和c2,对式(5)进行修改,如式(6)所示。
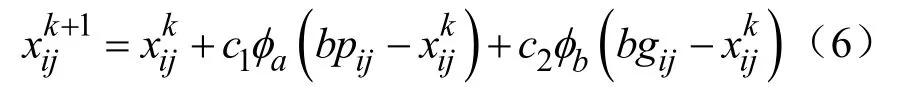
其中,
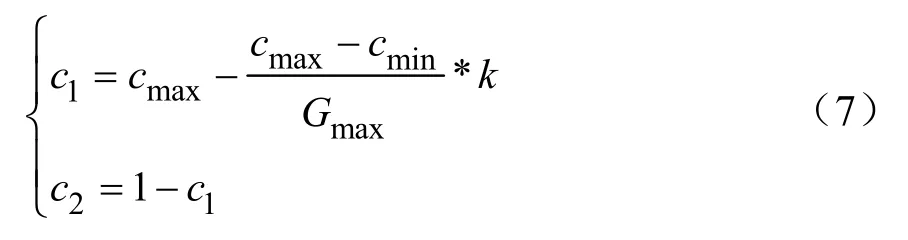
式中,cmax、cmin为学习因子的上、下限,cmax、cmin∈[0,1];Gmax为最大迭代次数;φa、φb为[-1,1]之间的随机数;bpij为当前最佳位置,bpij=(bpi1,bpi2, … , bpiD);bgij为全局最佳位置,bgij=(bgi1,bgi2,…,bgiD)。
所以,保持BABCA 的基本结构和参数不变[24],用式(6)代替式(5),构建改进人工蜂群算法IABCA,运算流程如下:
Step1:初始化IABCA 基本参数:对N、Gmax、cmax、cmin、φ、D、L、bpij和bgij赋值,产生初始解集;
Step2:计算每个蜜源的适应度值fit,其中适应度好的选为跟随蜂,剩下的为引领蜂,并记录最优值;
Step3:引领蜂搜索新蜜源,根据式(6),产生新的可行解;
Step4:跟随蜂计算该可行解的选择概率,并在[0,1]内随机产生一个数。若该可行解的概率值大于该随机数,则跟随蜂由式(6)产生一个新解,反之,保存该可行解。并检验其适应度值fit;
Step5:若fit Step6:若一个解经过L 次循环都未更新,则该解被舍弃,该解对应的引领蜂转化为侦查蜂,侦查蜂根据式(6)产生新解,取代旧解; Step7:对算法终止条件进行判断:若k<Gmax,则返回Step3,继续迭代运算。否则算法结束,输出全局极值坐标()和最优适应度值fit*。 这样,在IABCA 执行的前期,c1较大(c2较小),能增加引领蜂的全局搜索范围和种群多样性。随着迭代次数k 的增加,在算法执行的后期,c2渐增(c1渐减),有利于在算法执行的后期,收敛到全局最优解gbest。该IABCA 可用MATLAB 软件进行编程,命名与保存为一个文件IABCA.m。 为了验证IABCA 的有效性,选取典型测试函数Rastrigin[25],如式(8)所示。 式中,f(x)为多峰函数,xi∈[-5.12,5.12]。理论全局最小值点,仅在(x1,x2,…,xD)=(0,0,…,0)处取0。 所以将min f(x)作为适应度函数J,对BABCA和IABCA 进行验证。其中BABCA 和IABCA 相关参数设置如表1 所示。 表1 BABCA 和IABCA 的参数设置Table 1 The values of parameter for BABCA and IABCA 另外为了增强对比,再引入文献[25]中的粒子群优化算法(Particle Swarm Optimization Algorithm,PSOA)和布谷鸟搜索算法(Cuckoo Search Algorithm,CSA),保持其基本结构和参数不变,分别将PSOA、CSA、BABCA 和IABCA 作用于该Rastrigin 函数。4 种算法分别运行30 次,相应的统计结果和min f(x)迭代过程如表2 和图3 所示。 图3 基于四种算法的J 进化过程Fig.3 Evolution process of J based on four algorithms 表2 BABCA 和IABCA 对Rastrigin 函数优化结果Table 2 Optimization results of Rastrigin function solved by BABCA and IABCA 分析表2 可知,IABCA 求解的min f(x)的最优值、最差值、中间值、平均值和标准误差的结果,均好于PSOA、CSA、BABCA,另外基于建筑环境与能源测试技术的误差分析方法[26],在置信度99.7%情况下,IABCA 求解的min f(x)结果区间,也优于其他三种算法。另外分析图3,可见四种算法作用下的Rastrigin函数适应度值J变化趋势整体上是一致的,但是IABCA 作用下的J 变化更贴近理论极值点0,搜索速度更快,说明IBACA 的收敛性要优于PSOA、CSA、BABCA,因此也验证出本文构建的IBACA 性能是优于一般算法的。 如上所述,CT-FOPIDC 的参数整定密切冷凝温度的调节品质。本节选择min ITAE 作为IABCA目标函数: 来设计PIλDμ控制器参数整定的算法,相应的算法执行流程如下: Step1:初始化IABCA 相关参数:对N、Gmax、cmax、cmin、φ、D、L、bpij和bgij赋值; Step2:根据Z-N 整定法计算出PIλDμ控制器参数的初始值[KP0,KI0,KD0]和λ0=μ0=1,即y0=[KP0,KI0, KD0, 1,1]置入MALAB/Simlink 工具组态中的PIλDμ控制器,且设定KP、KI、KD、λ和μ的上下限; Step3:输入闭环负反馈PIλDμ控制系统的反馈信号e(t),产生初始解集,基于min ITAE 计算每个可行解y=[KP,KI,KD,λ,μ]的适应度值fit; Step5:若fit Step6:舍弃经过L 次循环都未更新的解,该解对应的引领蜂转化为侦查蜂,侦查蜂根据式(6)产生新解取代旧解; Step7:若k<Gmax,则返回Step3 继续迭代运算,否则,输出PIλDμ控制器参数最优值,即y*=[KP*,KI*,KD*,λ*,μ*],min ITAE 最优解以及相应的闭环负反馈PIλDμ控制系统动态响应曲线。 使用MATLAB 软件,对上述基于IABCA 的PIλDμ控制器参数整定算法进行编程,保存并命名为IABCA.m 文件,同时借助MATLAB/Simlink 工具进行闭环负反馈PIλDμ控制系统进行组态,并与IABCA.m 同步运行。 为了验证本节所设计的PIλDμ控制器参数整定算法-IABCA.m,选用文献[14]中的二阶传递函数,如式(10)所示。 作为被控对象,并设计一个单位闭环负反馈PID 控制系统作用于它。分别运用IABCA、BABCA和Z-N 整定法对该控制系统中的PID 控制器参数进行整定,相应的结果如表3 所示,并输出其动态响应曲线,如图4 所示。 表3 PID 控制器3 个参数整定结果Table 3 Results of tuning three parameters for PID controller 分析表3 和图4 可知,基于IABCA 整定的PID控制器参数[KP*,KI*,KD*,λ*,μ*],其控制效果要明显优于BABCA 和Z-N 整定法。而基于BABCA和Z-N 整定法作用下的单位闭环负反馈PID 控制系统,对应的动态响应均存在较大的超调量且调节时间较长。这表明本节设计的基于IABCA 的PIλDμ控制器参数整定算法是可行的,也为下节冷凝温度PIλDμ控制系统及其参数整定的数值模拟,奠定了基础。 图4 不同PID 控制器参数值的单位闭环负反馈控制系统动态响应Fig.4 Dynamic responses of a unit closed-loop negative feedback PID control system with different values of controller’s parameters 根据空调工艺的相关要求,夏季制冷工况下的流经冷凝器的冷却水供、回水温度为32℃/37℃,冷凝温度设定值Tc,set=36 ℃,初始冷凝温度Tc,0=50℃[27]。借助MATLAB/Simulink 工具,根据图2 的基于IABCA 的冷凝温度PIλDμ控制系统方框图,对本文基于IABCA 的冷凝温度PIλDμ控制系统进行组态,如图5 所示。 图5 基于IABCA 的冷凝温度PIλDμ控制系统Simulink 模型Fig.5 Simulink model of condensation temperature PIλDμ control system based on IABCA 首先,IABCA.m参数设置与2.2中的相关部分相同。设定CT-FOPIDC的5个参数范围:KP∈[100,300],KI∈[5,35],KD∈[160,220],λ∈[0.5,1.8],μ∈[0,1]。然后同步运行图5所示冷凝温度PIλDμ控制系统Simulink模型和IABCA.m,可得冷凝温度Tc过渡过程,如图6中黑色实线所示。相应的[KP*,KI*,KD*, λ*, μ*]=[163.2569, 9.7856, 195.8580, 0.8828,0.7997]和最佳min ITAE=1085。 其次,BABCA.m参数设置与2.2中的相关部分相同,CT-FOPIDC的5个参数范围同上。然后同步运行图5所示冷凝温度PIλDμ控制系统Simulink模型和BABCA.m,也得到Tc过渡过程,如图6中所示。相应的[KP*, KI*, KD*, λ*, μ*]=[278.5965, 32.7512,198.5630,1.5123,0.8900]和最佳min ITAE=1383。 最后,应用Z-N整定法,离线计算出冷凝温度PID 控制器参数[KP, KI, KD]=[145.7635, 9.8175,202.2150],将[145.7635,9.8175,202.2150,1,1] 设置到图5所示冷凝温度PIλDμ控制器。然后运行图5所示冷凝温度PIλDμ控制系统Simulink模型,同样可得到Tc过渡过程,如图6中所示。 图6 三种PIλDμ控制器参数整定方式作用下的冷凝温度响应曲线Fig.6 Response curves of condensation temperature under three types of tuning parameters of PIλDμ controller 分析图6 可知,相比基于Z-N 整定法(λ=μ=1)和BABCA 这两种PIλDμ控制器参数整定方式,采用IABCA 方式所得到的冷凝温度Tc响应曲线,无论是在最大偏差、调节时间以及超调量,表现的都比其他两种方式要更好,且稳态误差ΔTc为0℃,说明采用IABCA 的控制效果优于一般控制方法。 采用Z-N 整定法(λ=μ=1)、BABCA 和IABCA对本文冷凝温度PIλDμ控制器进行参数整定,得到Tc相应的控制指标如表4 所示。 分析表4 可知,采用IABCA 对PIλDμ控制器参数进行整定,得到的冷凝温度相应的各项控制指标都要优于Z-N 整定法和BABCA,冷凝温度达到设定值的过程中所需的时间更短、波动更小,说明基于IABCA 对本文的冷凝温度PIλDμ控制器进行参数整定,有效提升了系统的控制质量。 表4 冷凝温度控制性能指标比较Table 4 Comparison of control performance indexes for condensation temperature 针对VCRU中冷凝温度被控对象,为了达到有效控制冷凝温度的目的,本文提出了一种基于IABCA的冷凝温度PIλDμ控制策略。引入基本人工蜂群算法BABCA,对算法更新公式进行改进,同时在此基础上提出线性变化的学习因子c1和c2改善算法搜索性能,构建出改进人工蜂群算法IABCA。一方面通过多峰测试函数Rastrigin验证其性能,统计结果表明IABCA求解的minf(x)的最优值和平均值都更接近理论值,且标准误差更小,说明IABCA在寻优性能方面优于BABCA。另一方面通过对PID控制器参数进行整定,通过单位闭环负反馈控制系统动态响应结果对比,表明IABCA在控制器参数整定效果方面优于BABCA和Z-N整定法。最后采用IABCA对本文的冷凝温度PIλDμ控制系统进行参数整定,获取[KP,KI,KD,λ,μ]五个参数的最优值以及目标函数ITAE 的最优解,并借助MATLAB/Simulink进行模拟。结果表明:采用IABCA得到的各项控制指标都优于BABCA和Z-N整定法,冷凝温度响应曲线的最大偏差、调节时间以及超调量也比其他两种方式表现更好,并且达到Tc=Tc,set的控制要求。说明本文基于IMBCA的冷凝温度PIλDμ控制策略在理论上是可行的,且相应的冷凝温度也能满足空调工艺的相关要求。2.2 基于经典测试函数对IABCA 的验证

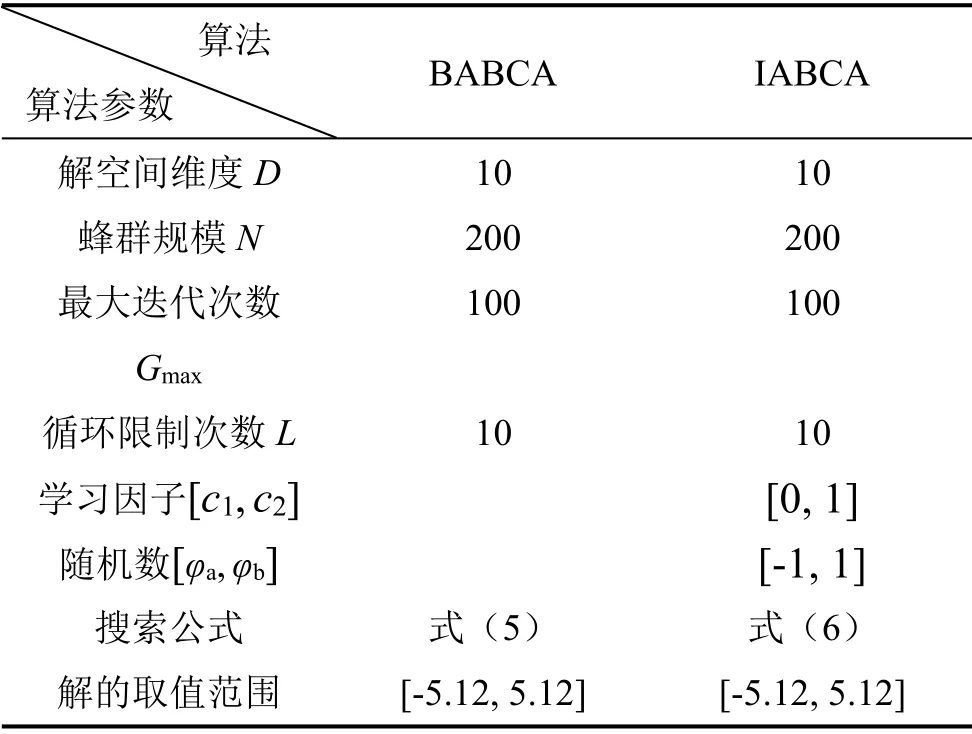
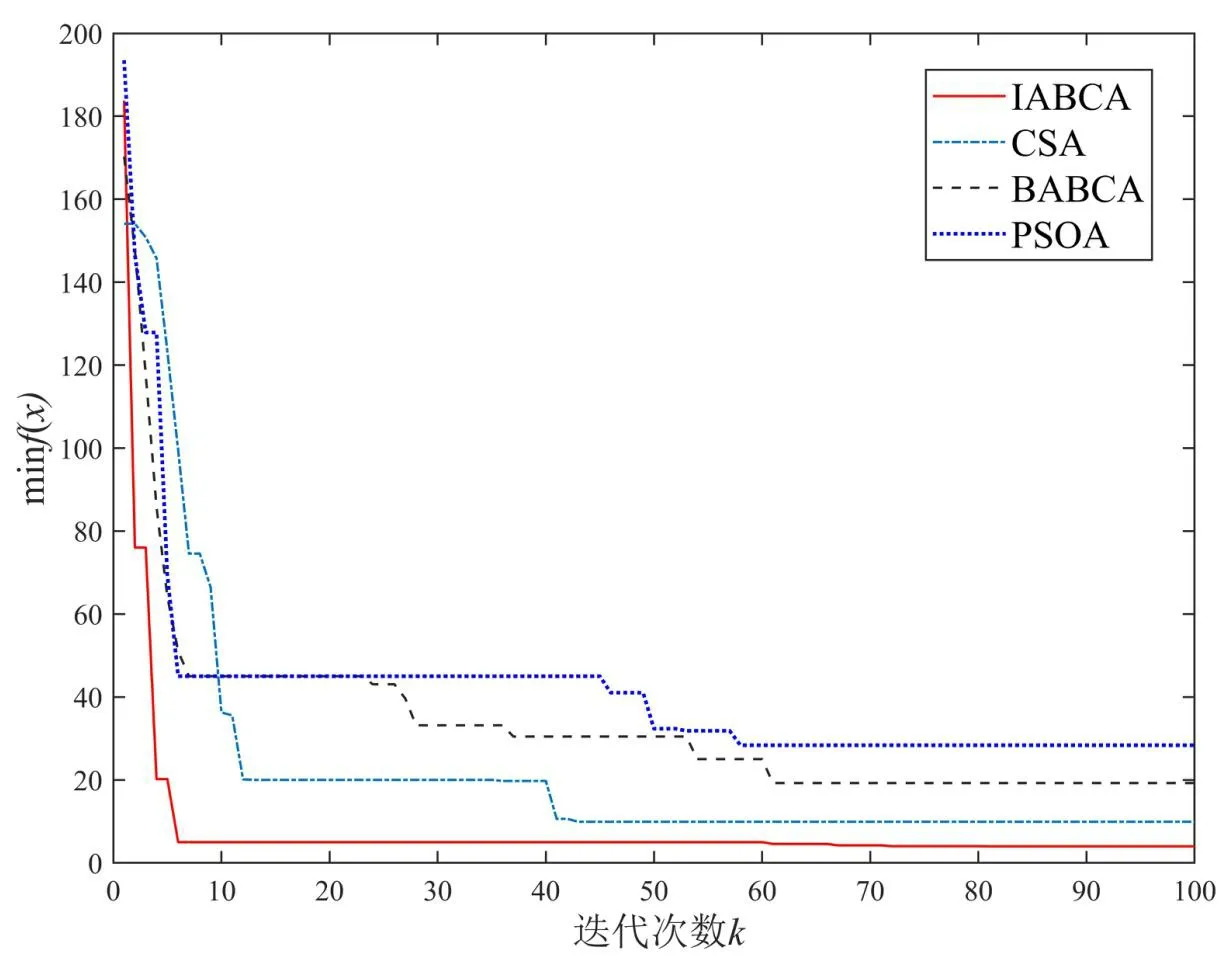
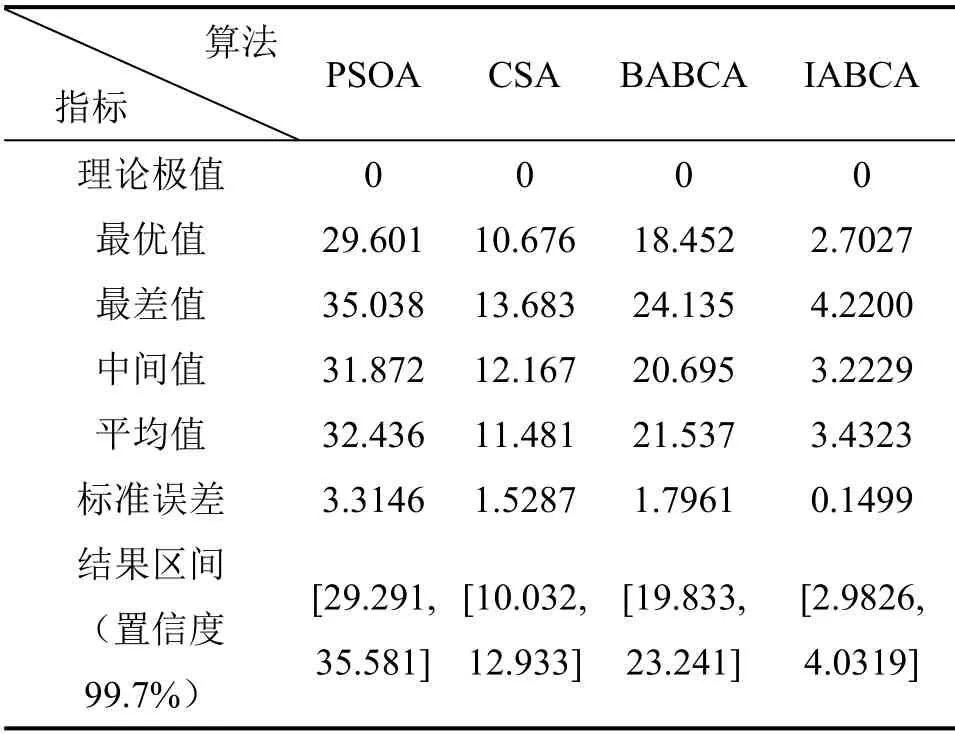
2.3 基于IABCA 的PIλDμ控制器参数整定


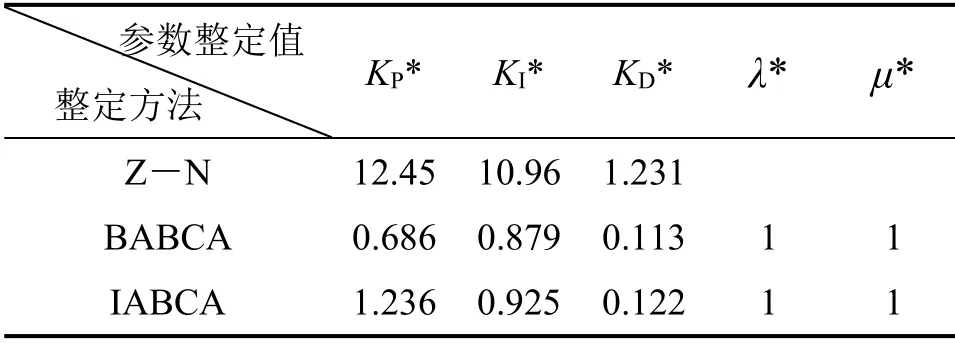

3 数值模拟
3.1 冷凝温度PIλDμ控制系统仿真

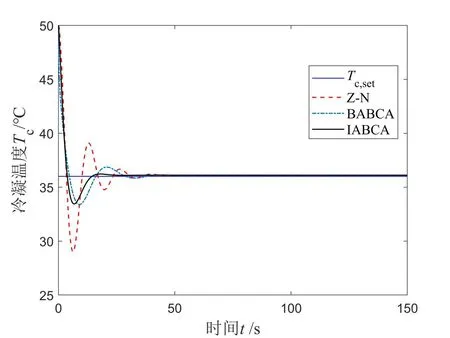
3.2 三种控制器参数整定的控制效果比较
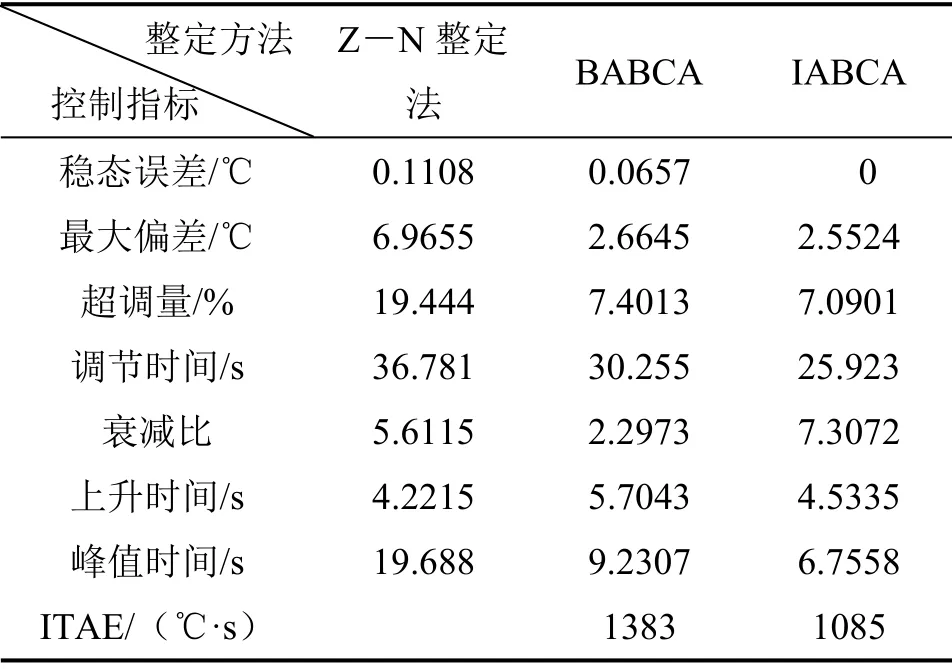
4 结论
