一种去除椒盐噪声的混合正则化模型

2022-09-20王佳佳唐利明

科技创新与应用 2022年26期

王佳佳，唐利明

（湖北民族大学，湖北恩施 445000）

在图像成像[1]、传输和储存的过程中，图像常常会受到外界的信息干扰，例如，在一些遥感图像设备中，由于外界环境存在电磁干扰，往往会使得成像后的图像含有一定程度的椒盐噪声，使得图像质量下降，导致后续图像处理更加困难（对图像的分析和理解造成较大干扰）。因此对于含有椒盐噪声的图像进行去噪处理是十分关键的。主要有以下几种方法：基于滤波器、基于各向异性扩散（P-M）方程和基于变分正则化的方法。其中，基于变分正则化的方法能有效地利用图像的先验信息，具有很强的可解释性。因此，在1992年，Rudin等[2-3]提出著名的全变分（Total Variation，TV）模型：该模型允许在超平面上重建不连续的图像，且有较好的去除噪声和保持边缘的能力。缺点：①模型中正则项非光滑，不可导，导致模型求解困难；②重建的图像有明显的阶梯效应；③在去噪过程中纹理等细节信息常常被当作噪声过滤掉，导致图像过模糊。为了克服上述问题，许多学者对TV正则项进行了改进，并提出了一些新的模型，例如：高阶全变分模型、广义全变分模型和分数阶各向异性扩散模型等。

Chan等[4]在2000年提出高阶全变分（High-Order Total Variation，HOTV）模型，该模型通过在TV模型的欧拉-拉格朗日方程中加入一个非线性四阶扩散项，有效减少了块伪影的数量，保持图像的跳跃不连续性，但在去噪过程中会导致边缘过模糊。随后，You等[5]提出四阶偏微分方程的去噪模型，该模型利用强度函数的拉普拉斯递增函数构成的泛函导出四阶偏微分方程，能够避免块状效应，在去噪和保持边缘之间取得较好的平衡。由于各向异性扩散算法容易产生多个假边缘，存在散斑现象。Bredies等[6]在此基础上提出广义全变分（Total Generalized Variation，TGV）模型，该模型引入函数u的高阶导数，减少块状效应，但在非平滑区域的边缘附近存在假边缘，即图像过模糊现象。2007年，Bai等[7]提出分数阶各向异性扩散（Fractional-Order Total Variation，FOTV）模型，该模型通过定义图像强度函数的分数阶导数绝对值的递增函数为损失函数，再采用折叠算法来消除跨越边界的跳跃不连续，能够较好地处理图像的纹理细节信息，但复原后的图像边缘部分信息保留不完整。

本文基于全变分模型保持图像边缘的优势，以及分数阶全变分模型能够抑制阶梯效应和保护图像纹理细节信息的特点，将全变分正则化子和分数阶正则化子相结合，提出了一种去除椒盐噪声的混合正则化模型（A Hybrid Regularization Model，AHRM）。该模型克服了传统的全变分模型存在阶梯效应和分数阶模型在去噪的同时过多损失边缘信息的弱点，在有效去除图像中椒盐噪声的同时，很好地保持图像的边缘和纹理细节信息，减少阶梯效应。本文所提出的AHRM模型是基于变分框架的，因此ADMM可以有效地求解该模型。大量的数值结果表明，AHRM模型在图像去噪方面都优于其他经典模型，本文模型较好地复原图像纹理信息，保留图像的不连续性和抑制块伪影。

1 相关背景

1.1 基于L1范数的全变分模型

2005年，Chan等[3]人提出了基于L1范数的全变分图像去噪模型。该模型正则化过程中对图像特征对比的依赖小于对图像形状的依赖，可以有效保留图像的不连续性和结构，能够较好地复原图像的真实信息，其去除椒盐噪声的变分模型为

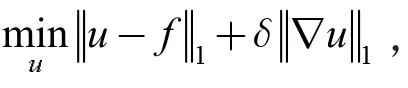
式中：u为待求图像；f为噪声图像；∇u为u的梯度算子；δ为权重参数。

基于L1范数的全变分模型在图像去噪过程中能有效复原图像的原有信息和保留图像边缘，更好分离图像的高频成分，如噪声和纹理。缺点：①由于梯度算子仅能刻画图像水平和竖直方向的信息，使得该模型处理图像局部结构特征时缺乏自适应性；②该模型将图像正则为分段常值函数，从而导致“阶梯”现象。

1.2 分数阶全变分模型

由于TV模型在图像复原过程中会存在阶梯效应，基于此，Bai等[7-10]在2007年提出分数阶各向异性扩散的图像去噪模型。

分数阶导数的定义为

则离散的分数阶全变分定义为

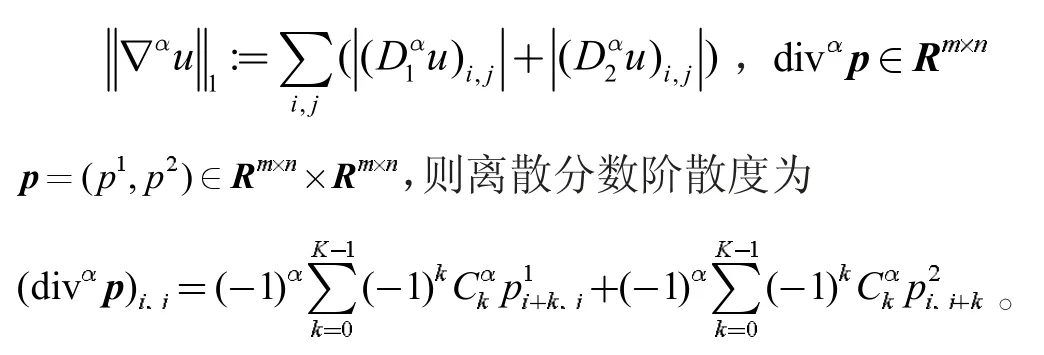
离散分数阶梯度和散度满足如下关系式

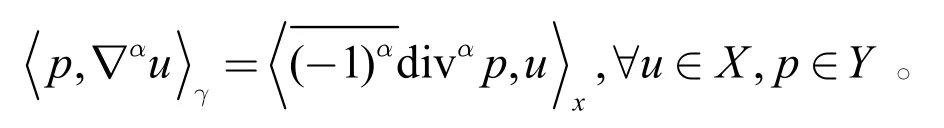
分数阶去除椒盐噪声的变分模型为

分数阶各向异性扩散模型有效保留图像的重要纹理细节信息，分数阶导数不仅非线性地保留了图像光滑区域的轮廓特征，还保留了边缘、纹理等高频成分。缺点：①图像的边缘部分的信息不能很好地复原；②分数阶梯度算子需要大量的实验来确定最优阶数。

2 本文模型与算法

2.1 本文模型

本文基于FOTV正则化子和TV正则化子提出一种去除椒盐噪声的混合正则化模型为

2.2 模型求解

利用ADMM[11]算法对式（1）进行求解，即利用该模型的可分结构对该模型进行分离变量求解，通过引入辅助变量ν，p，q，并将其转化为下述约束优化问题。

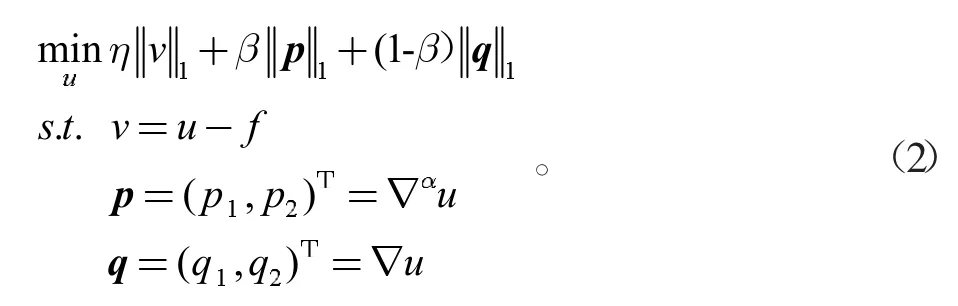
然后构造增广拉格朗日函数，可将式（2）的最小化转化为下面的鞍点问题。即

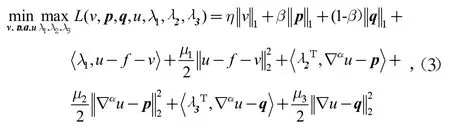
式中：λ1，λ2，λ3为拉格朗日乘子；μ1，μ2，μ3为惩罚参数；<·，·>定义为内积。进一步得到

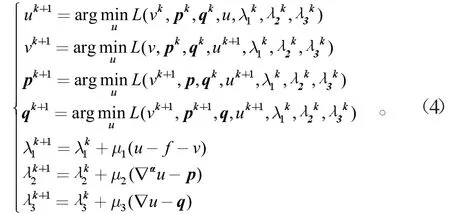
下面求解各个子问题。

（1）求解u-子问题，即求解下面方程

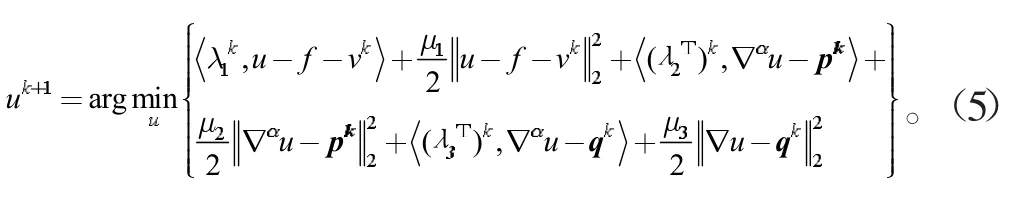
该问题为光滑凸优化问题，对式（5）关于u求偏导可得

式中：F和F-1分别表示傅里叶变换及其逆变换，此处的矩阵除法、平方和绝对值都是按分量运算的。

（2）求解ν-子问题，利用收缩算子给出ν-子问题的闭形解，即求解下面这个极小值问题

满足收缩算法的条件，可得

（3）求解P-子问题，类似求解子问题ν。即求解下述极小值问题

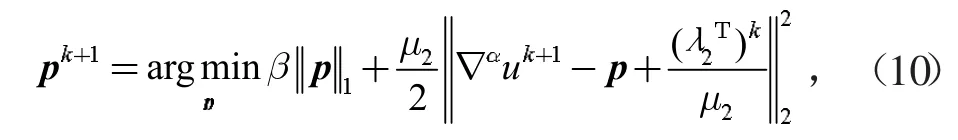
满足收缩算法的条件，有

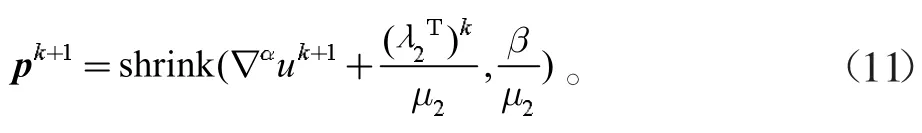
（4）求解q-子问题，跟上式算法相同。即求解下述极小值问题

满足收缩算法的条件，可得

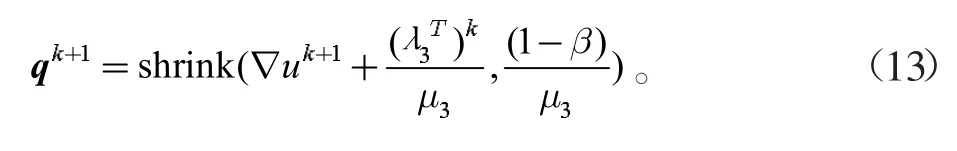
对提出模型求解过程如下。

初始化阶段：输入初始图像u0=f，设置参数的初始值为k=0；φ=0.6；α=1.6；β=0.7；μ1=0.4；μ2=0.3；μ3=0.4，最大迭代次数maxiter=800，迭代精度ε=10-6。

迭代循环过程如下。

Step1：初始化k=1，ε=10-6；

Step2：通过式（7）更新子问题中的uk；

Step3：通过式（9）更新子问题中的νk；

Step4：通过式（11）更新子问题中的pk；

Step5：通过式（13）更新子问题中的qk；

Step7：k=k+1。

终止：若迭代精度ε小于10-6或者迭代次数到达800则该算法终止，否则继续上述迭代循环过程。

3 实验及分析

实验在LAPTOP-RETV7IRD Aspire A515-516Intel（R）Core（TM）i5-7200U CPUⓒ2.50 GHz 2.71 GHz RAM 4.0 G matlab2014a环境下进行。使用matlab内置函数“Imnoise”对图像分别添加10%、30%、50%的椒盐噪声，再分别利用FOTV、HOTV、TV和本文模型（AHRM）4种模型对其去噪。本文利用图像的峰值信噪比（Peak Singal to Noise Ratio，PSNR）和结构相似性（Structual Similarity，SSIM）2个评价标准来评价去噪后的图像，二者值越大则说明去噪效果更好。本文选取的测试图像结构特征明显、纹理信息丰富，如图1所示，其中图1（a）和图1（b）为遥感图像[12]。

图1 测试图像

4 AHRM模型在椒盐噪声为10%、30%、50%下的去噪效果

4.1 AHRM模型在椒盐噪声为10%下的去噪效果

为了验证所提模型的去噪能力，选取含有强度为10%椒盐噪声的图像作为实验对象，实验结果如图2所示。

图2 不同图像在强度为10%的椒盐噪声下去噪效果对比

在强度为10%的椒盐噪声下，TV对纹理信息的损失严重，窗户、墙体及阳台的信息存在一定程度的模糊，FOTV复原后的图片边缘信息损失严重，经过HOTV复原后的图片窗沿部分存在失真现象。而AHRM模型不存在边缘过模糊，且能较好地复原图像的纹理信息，窗户、墙体及中间的楼轮廓更为清晰。由表1可知，FOTV复原后的图像的PSNR值和SSIM值较低，AHRM复原后的图像的PSNR值和SSIM值最高，其PSNR值和SSIM值分别高于TV 0.75 dB和0.04，进一步验证了本文模型的有效性。

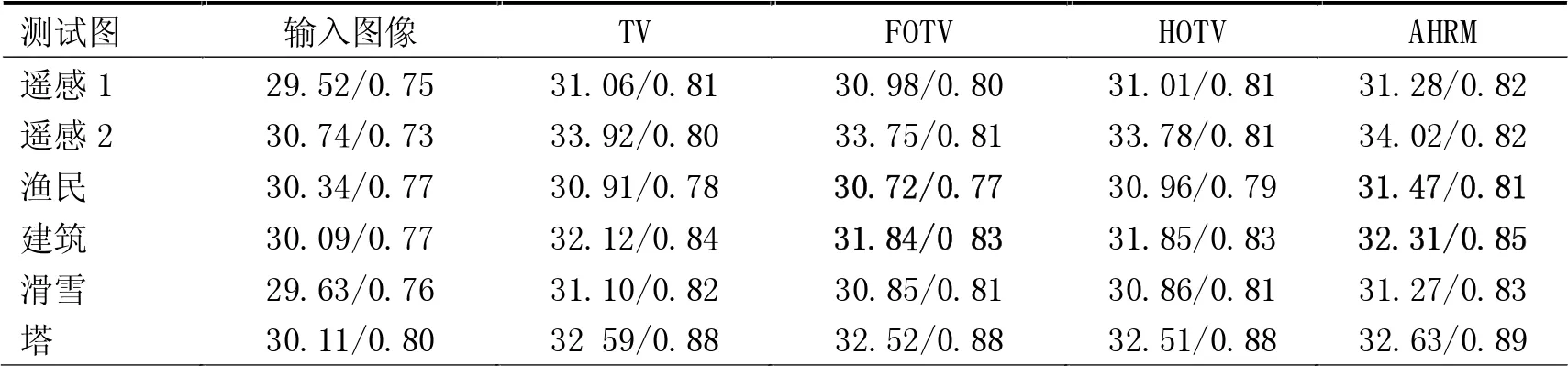
表1 不同模型在强度为10%的椒盐噪声下去噪结果的PSNR和SSIM对比

4.2 AHRM模型在椒盐噪声为30%下的去噪效果

为了验证所提模型的去噪能力，选取含有强度为30%的椒盐噪声的图像作为实验对象，实验结果如图3所示。

由图3可知，与其他模型相比，AHRM的模型可以很好地保持图像的结构和边缘，并产生令人满意的去噪结果。FOTV及HOTV复原后的图片，船体、船杆及湖面部分的失真较大，且边缘部分存在一定的模糊，TV重建后图像可以看到明显的“阶梯现象”。而AHRM对船体和船杆的复原效果最好，由表2可知，本文模型去噪后的PSNR值和SSIM值优于其他模型，PSNR值和SSIM值分别高于FOTV 0.59 dB和0.04，由客观指标可以看出，AHRM有效抑制阶梯效应，保留图像边缘及较好地复原图像纹理细节信息。

表2 不同模型在强度为30%的椒盐噪声下去噪结果的PSNR和SSIM对比

图3 不同图像在强度为30%的椒盐噪声下去噪效果对比

4.3 AHRM模型在椒盐噪声为50%下的去噪效果

为了验证所提模型的去噪能力，选取含有强度为50%的椒盐噪声的图像作为实验对象，实验结果如图4所示。

由图4对比可知，在强度为50%的椒盐噪声下，椒盐噪声对图像的结构破坏较为严重，如塔图的塔顶及塔的轮廓边缘部分信息被重建后依旧被破坏较为严重，且其整体视觉效果略差于强度为10%和30%的图像。经FOTV处理后塔的边缘轮廓不清晰，经HOTV复原的图像可看出每层楼之间的分界部分不清晰且楼体边缘过模糊，TV复原的图像失真较大。AHRM可以更好地复原图像纹理信息，分界部分更加清晰，边界轮廓也复原得更好，同时由表3数据进一步说明本文提出的AHRM模型具有更好的图像复原性能。