基于小应变土体硬化模型的水工隧洞围岩稳定性研究

贾晶玺， 于 奎， 黄 勇， 盛健挺， 梁江晟， 孟凡香

（1.黑龙江大学水利电力学院，哈尔滨 150080； 2.黑龙江省水利水电勘察设计研究院，哈尔滨 150080）

有限元数值分析是解决实际复杂岩土工程的重要手段，而影响数值计算结果可靠度的重要因素便是土体本构关系的选择和材料参数的确定. 对于软土较多的基坑工程来说，选用已经发展成熟和应用广泛的小应变土体硬化模型（简称HSS模型）能够解决土体在小应变阶段的一系列变形问题. 小应变土体硬化模型已经经过大量实际基坑工程验证，被基坑工程技术标准推荐使用［1］. 但是目前大量的软弱土体地质条件下的水工隧洞工程中仍常采用摩尔库伦弹塑性模型，对小应变土体硬化模型应用较少.

国内外大量研究和工程实例表明，在地下结构开挖过程中，除少数区域发生塑性变形或破坏以外，大部分区域为小应变状态［2-4］. 小应变是指应变值较小，范围为10-5～10-2. Jardin等［5］通过对大量土体变形试验研究确定土体小应变具有高刚度、非线性等特点. 采用常规线弹性或摩尔库伦模型很难准确预测小变形情况下的非线性特征以及土和结构相互作用的变形情况. 小应变土体硬化模型不仅能反映小变形土体开挖问题中的卸载应力路径问题，而且可以反映软土的剪胀性与压缩硬化，因而更适用于模拟软土类复杂地质的开挖问题.

张晋勋等［6］对理想盾构隧道工程模型，利用正交试验进行了小应变土体硬化模型的多参数全范围水平取值的敏感性研究；施有志等［7］分析了厦门地区小应变土体硬化模型的小应变参数对地表沉降及基坑围护结构的影响；吴小斌等［8］利用HSS模型对常州某地铁车站深基坑工程进行了数值模拟；顾晓强等［9］系统研究了上海地区土体HSS模型参数的取值问题，并进行了工程验证；尹骥［10］利用上海地区两个深基坑工程实例验证了小应变土体硬化模型在深基坑数值计算中的可行性和参数的准确性. 基于HSS模型的基坑工程［11-13］和盾构隧道工程［14-15］的研究为采用小应变土体硬化模型研究水工隧洞稳定性问题提供了借鉴和参考.

1 小应变土体硬化模型

1.1 小应变土体硬化模型原理

小应变土体硬化模型（简称HSS 模型）是Benz［16］在硬化土模型的基础上综合考虑了小应变阶段土体特性改进得来的. 土体硬化模型是通过三轴压缩试验和固结试验提出的弹塑性模型，采用双曲线来拟合三轴压缩试验的应力应变关系. Benz 在硬化土模型的基础上，考虑了主偏量加载和主压缩带来的剪切硬化和压缩硬化，提出了小应变情况下应力应变关系的简单双曲线模型［16］. 图1为土体硬化模型标准排水三轴试验的应力应变曲线，其中，ε1为轴向应力；σ1-σ3为偏主应力.qf为摩尔-库伦剪切破坏强度值；qa是渐近线强度值；E50为50%强度时的割线强度；Eur为土体的回弹模量.

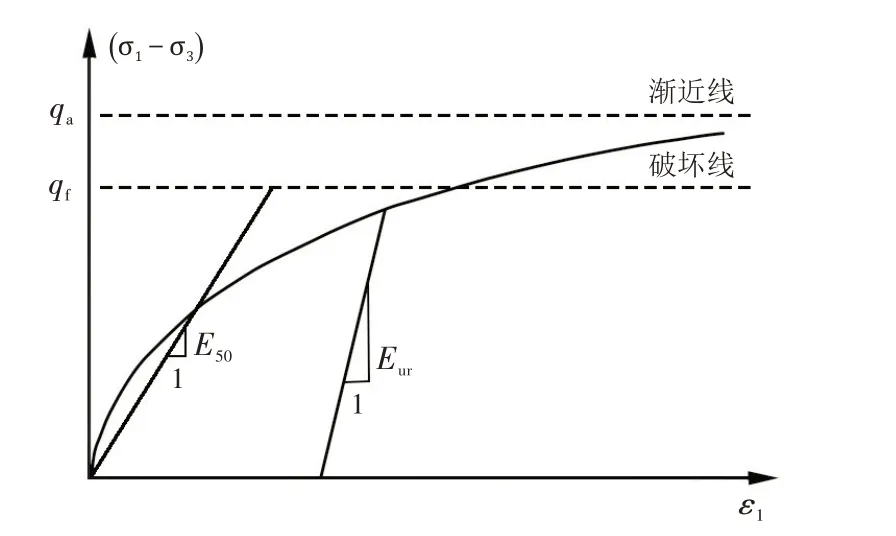
图1 土体硬化模型的应力-应变曲线Fig.1 Stress-strain curve of hardening soil model

在主应力空间中，HSS模型的硬化屈服面是随着塑性应变的增大而变大，不是完全固定的，其剪切屈服函数表达式为

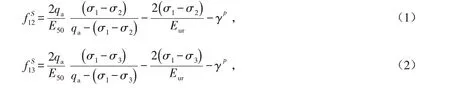
式中：γp为累积塑性剪切应变.小应变土体硬化模型除了具有硬化土模型所有的参数特征外，还引入参考剪切模量和小应变刚度系数γ0.7两个小变形量，来考虑土体在小应变阶段刚度较大的特性.

1.2 HSS 模型与其他本构模型的比较

常用的岩土本构模型有：线弹性模型、Druker-Prager 模型、摩尔-库伦模型、Duncan-Chang 模型、格里菲斯强度模型、霍克-布朗模型、硬化土模型以及小应变土体硬化模型等.

线弹性模型能够预测线性变形，但未考虑土体的非线性问题；Duncan-Chang模型是一种非线弹性模型，应用较广，参数易得，但不能很好地反映除压缩以外的其他应力路径问题，也没有考虑土的剪胀性；摩尔-库伦模型作为应用广泛的理想弹塑性模型，其参数比较简单并且获取容易，但未考虑卸载模量与加载模量的影响；Druker-Prager模型为弹塑性模型，参数简单易取，能分析土体的剪胀性，但未考虑固结压力的作用；格里菲斯强度模型与摩尔库伦模型有明显不同，认为岩土体破坏是脆性拉伸破坏，主要适用于坚硬脆性岩土体的破坏问题；硬化土模型（HS）考虑了岩土体的压缩性和剪胀性，但是未考虑土体在小应变状态下具有较大的刚度和刚度随应变增加而弱化的情况.

与其他本构模型相比，小应变土体硬化模型不仅考虑了软土的固结变化特性与刚度随应变增加而弱化的特征，而且考虑软土的压缩硬化与剪胀性，可以处理土体在小应变阶段刚度较大的问题. 小应变土体硬化模型更适用于对粉土、砂土、黏土等较软类地质的模拟.

1.3 HSS模型参数确定方法

小应变土体硬化模型共包含上述2个小变形参数和硬化土模型的11个参数. 综合参考相关研究［9，17-18］和理论，各参数定义以及取值方法如表1所示.

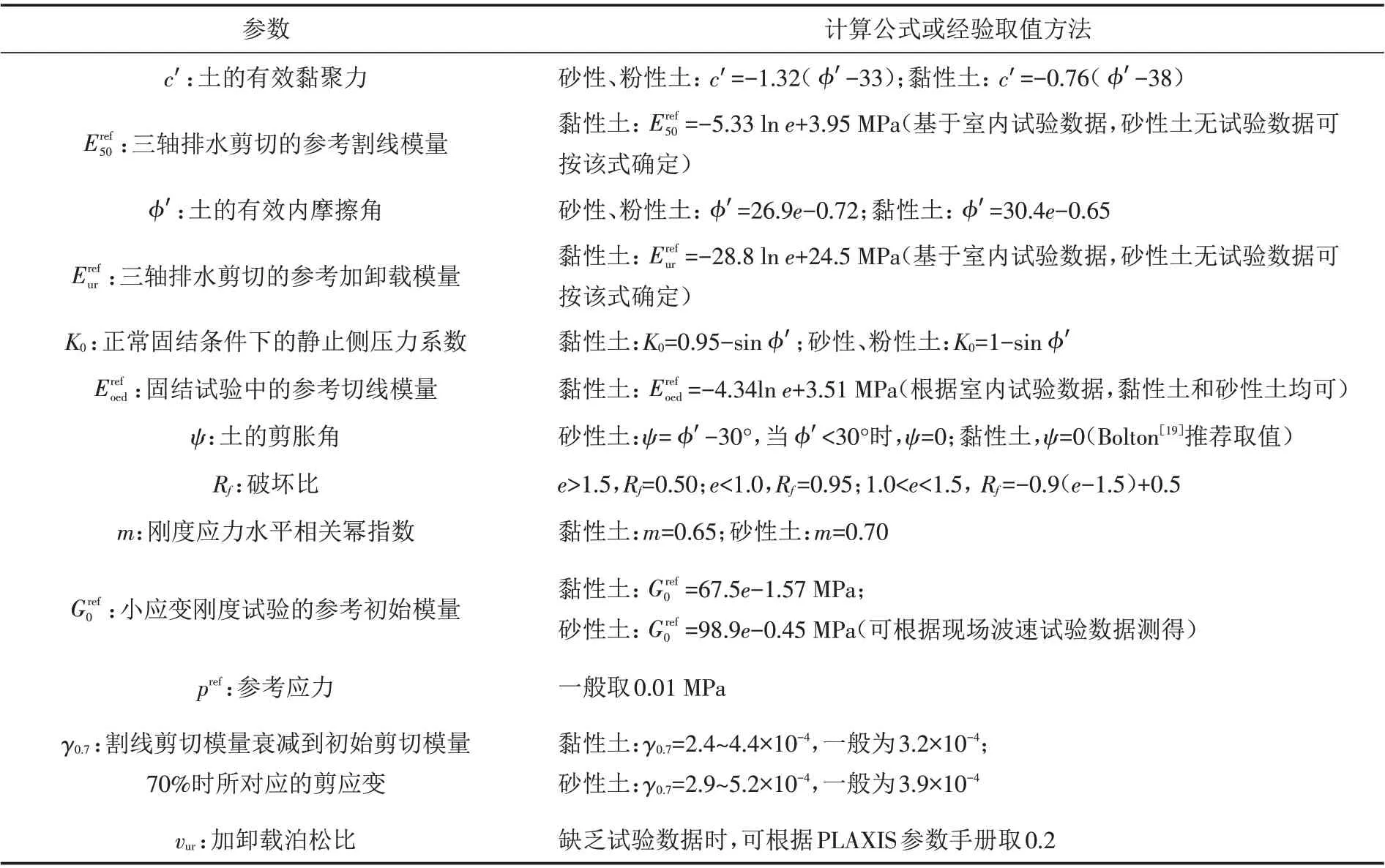
表1 HSS模型参数意义及取值方法Tab.1 Connotations of parameters in the HSS model and their determination methods

2 模型的建立与参数确定

2.1 工程背景

本研究是基于黑龙江省哈尔滨市通河县二甲沟水库引水隧洞工程. 隧洞设计长度2410 m，洞顶埋深约为25.1～30.9 m. 隧洞处于低山丘陵地区，隧洞沿线局部区域穿过山间台地. 大部分山体表层覆盖有机质低液限粉质黏土，下部为强风化和弱风化粗粒花岗岩. 局部地表为水田，土体受多年浸泡的影响，上层土体及岩体均处于饱水状态［20］. 该隧洞埋深浅，大部分岩土体为Ⅳ、Ⅴ类围岩，开挖施工期间隧洞变形较大，整体稳定性差，因此准确分析围岩变形情况尤为重要.

洞顶覆土由下至上可以分为弱风化花岗岩、强风化花岗岩、全风化花岗岩和粉质黏土四层. 根据地质勘查报告提供的土层参数如表2.

表2 土体勘查参数Tab.2 Soil investigation parameters

本次模拟分析采用PLAXIS 3D 建立模型.依据上述多种岩土本构模型适用范围，综合考虑各材料特性，粉质黏土、全风化花岗岩、强风化花岗岩为破碎软弱岩土体采用HSS 模型，弱风化花岗岩采用摩尔-库伦模型，支护结构混凝土衬砌采用线弹性模型来模拟. HSS模型中、、等参数需要标准排水三轴试验确定，实际工程勘查中难以提供. 结合勘查报告并参考相关研究［9］和经验公式，确定此工程的HSS模型部分参数如表3所示. 弱风化花岗岩和混凝土衬砌材料参数如表4所示.

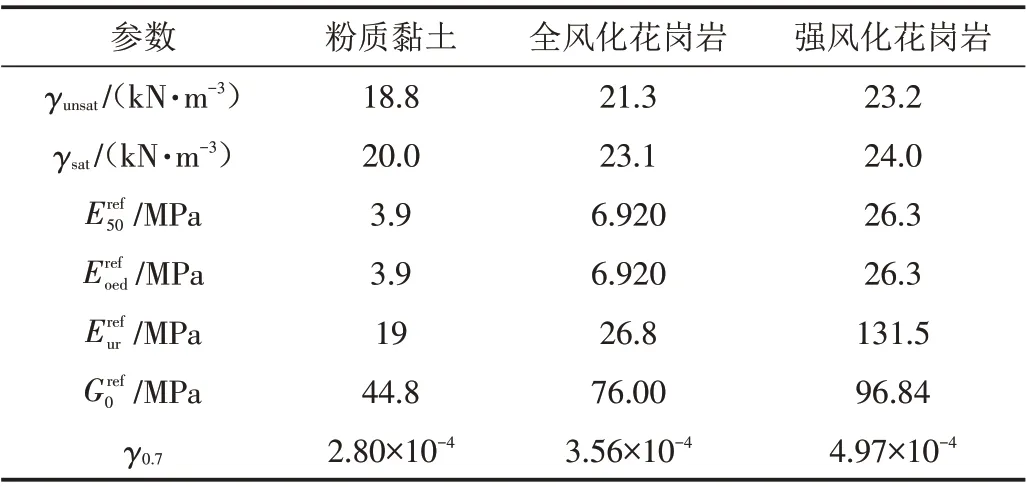
表3 HSS模型部分参数Tab.3 Partial parameters of model HSS

表4 部分岩体参数和结构参数Tab.4 Some rock parameters and structural parameters

2.2 模型建立

为研究该水工隧洞开挖在小变形阶段的应力和变形情况，选取二甲沟水库引水隧洞0+627～0+632段长度约30 m的隧洞作为计算模型. 该水工隧洞为无压隧洞，形式为圆拱直墙形，埋深约25.1 m，设计水深2.5 m，圆拱半径2.7 m，直墙段高度2.7 m，底宽5.4 m，洞身衬砌厚度40～80 cm. 隧洞采用边开挖边支护的方式施工.结构为钢筋混凝土衬砌，采用板单元模拟. 土体参数按表2和表3设置.

2.3 应力分析

本次模拟采用小变形土体硬化土模型来模拟隧洞分部开挖和支护. 隧洞围岩最大主应力分布如图2所示，在隧洞断面周围主应力最大值出现在两个底角处，另外侧墙与顶拱交接处也出现较大应力，这符合拐角处易出现应力集中的实际情况. 应当注意对较大应力区域进行加固，以防发展成塑性区而进一步崩塌破坏.

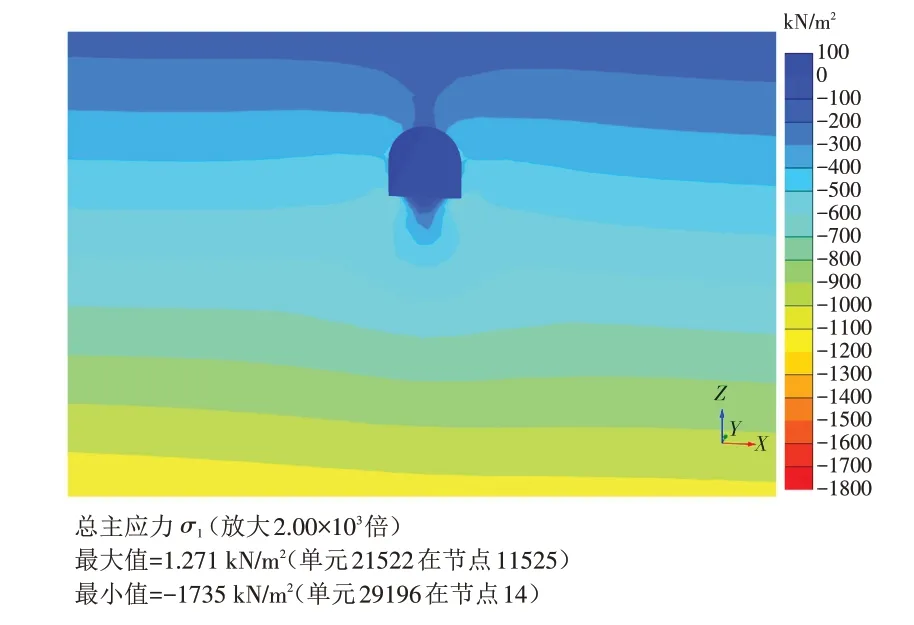
图2 隧洞断面周边最大主应力分布图Fig.2 Distribution of the maximum principal stress around the tunnel section

2.4 变形分析

隧洞开挖结束整体变形和隧洞洞顶沉降变形分别如图3和图4所示. 由于岩层松软，隧洞变形主要在拱顶和洞底，拱顶挤压出现大的下降变形，甚至可能出现松动掉块，洞底出现挤出鼓包变形，最大变形出现在洞底隆起变形达0.098 m.

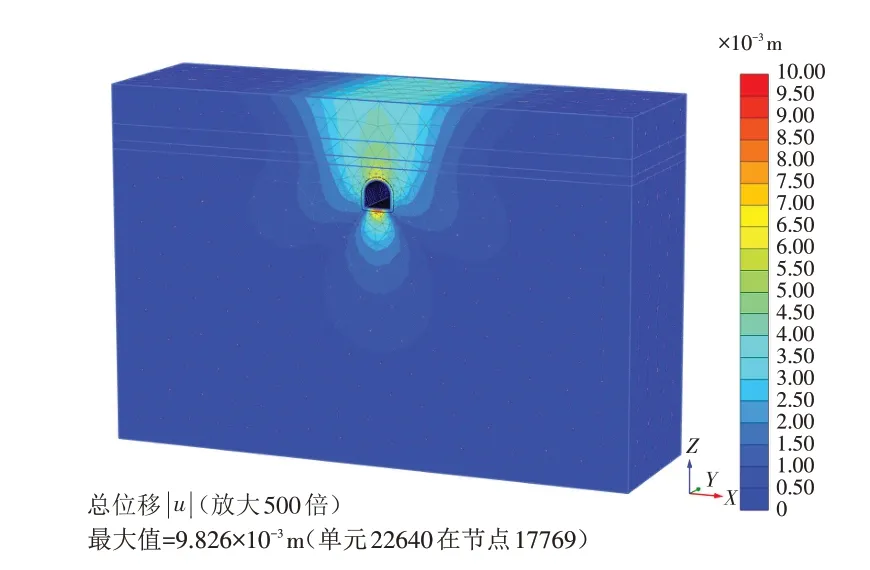
图3 隧洞整体变形图Fig.3 Overall deformation diagram of the tunnel

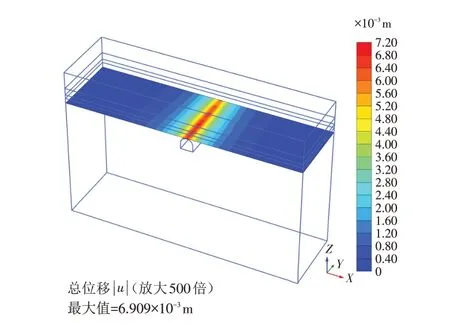
图4 隧洞洞顶沉降变形分布图Fig.4 Distribution diagram of settlement deformation at the top of the tunnel

为研究开挖过程中隧洞的变形特征，得到了不同施工开挖进尺的隧洞变形云图. 由图5 可见，隧洞变形随着施工的推进逐步增大，最后在整个模型区域均出现了明显的变形，顶部沉降变形和底部鼓包变形越来越大.

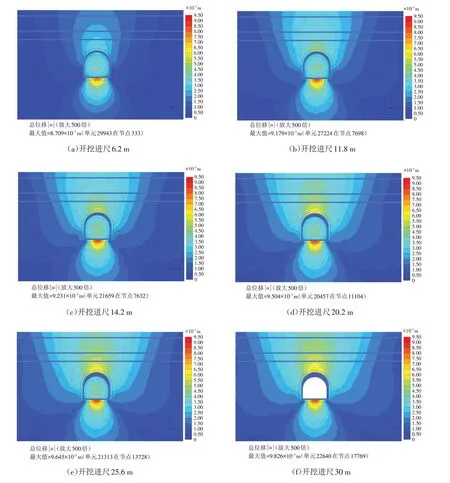
图5 不同施工开挖进尺的隧洞变形云图Fig.5 Cloud diagrams of tunnel deformation under different construction excavation levels

2.5 对比分析

采用摩尔-库伦模型和小变形土体硬化模型分别对该水工隧洞开挖工程进行数值模拟分析，获得水工隧洞顶部变形随开挖进尺深度的变化曲线（如图6 和图7），并根据实际监测数据进行对比验证. HSS 模型下，隧洞最大变形和顶部最大沉降位移分别为9.8 和6.9 mm；而摩尔库伦模型下，隧洞最大变形和顶部最大沉降位移分别为30.2 和9.1 mm. HSS 模型考虑了土体在小应变阶段特性，隧道开挖引起卸荷区域的变形模量会增大，土体变形反而会减小；而在传统的弹塑性模型（摩尔-库伦模型）中，土体的变形模量是恒定的.因而小变形土体硬化模型计算的结果和摩尔-库伦模型的结果是不一致的，小变形土体硬化模型计算的隧道顶部位移相对较小.

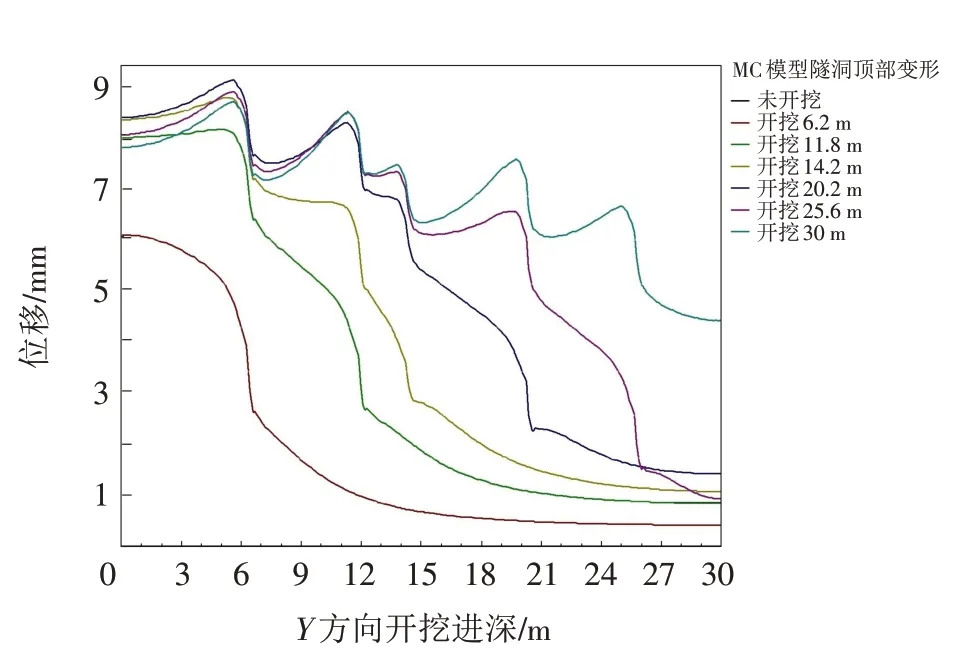
图6 摩尔库伦模型下的隧洞顶部变形Fig.6 Tunnel top deformation based on the Mohr-Coulomb model

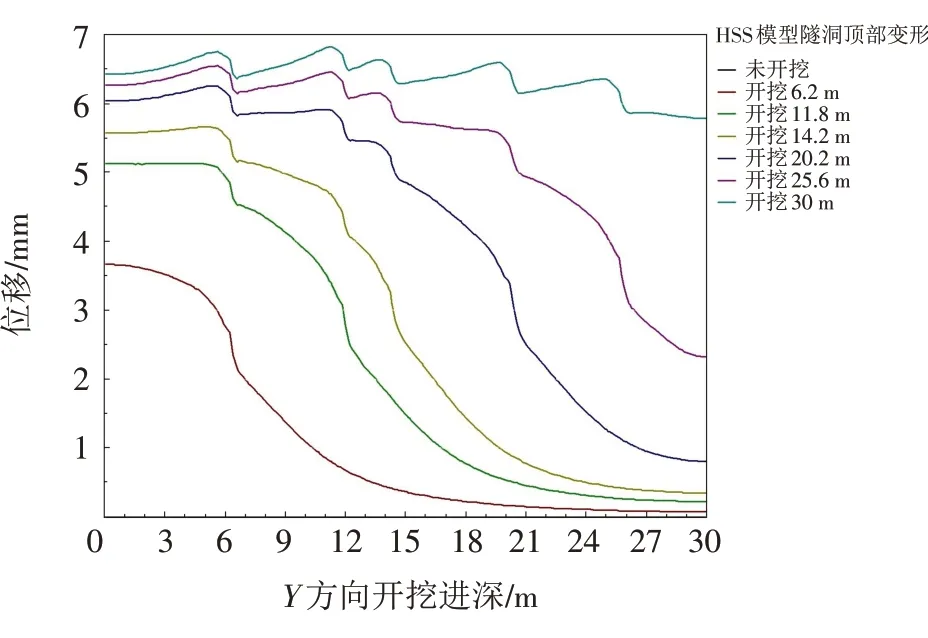
图7 小变形土体硬化本构模型下的隧洞顶部变形Fig.7 Tunnel top deformation based on the hardening soil model with small strain stiffness

从模拟分部开挖的各个阶段取得隧洞洞顶最大沉降变形数据绘得如图8 所示，显然，小变形土体硬化模型分析得到的隧洞顶部变形比摩尔库伦模型更小，更接近实际变形情况. 这说明HSS 模型分析出的变形量与实际监测最大沉降量数据吻合更好.

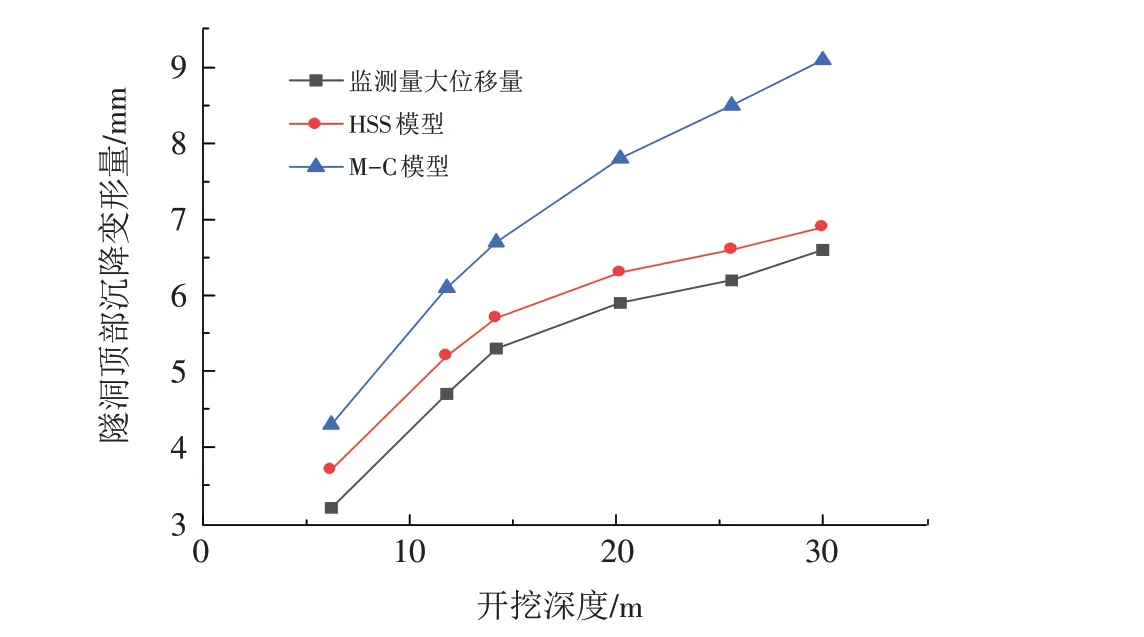
图8 隧洞顶部沉降变形对比Fig.8 Comparison of settlement deformation at the top of the tunnel

3 结语

1）本文通过理论分析，较好地模拟出了二甲沟水库引水隧洞的围岩变形情况. 在软弱土层的地质条件下，采用小变形土体硬化土模型对土体小变形阶段的模拟更接近实际情况，能够清晰地描述土体剪切硬化、压缩硬化情况，能为类似实际工程的方案设计与开挖支护提供参考和依据.

2）小变形土体硬化模型与摩尔-库伦模型相比，HSS模型考虑了土体卸载时其刚度增大的特性，能够更准确地描述土体的塑性特征和小变形情况，但是其实际使用难度在于土体参数的选择与确定［21］. 因此小变形土体硬化模型在后续的推广和应用中，关键问题在于参数选取的简化，使之更便于实际工程使用.