有意电磁干扰辐照下电子设备响应的∞范数上确界评定方法

2022-09-20梁涛谢彦召席志豪

西安交通大学学报 2022年9期

梁涛,谢彦召,席志豪

(1.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2.西安交通大学电气工程学院,710049,西安)

有意电磁干扰(intentional electromagnetic interference,IEMI)是以干扰、毁伤电子设备为目的,人为恶意制造的电磁环境,对设备的电磁安全构成了巨大威胁[1-4]。随着脉冲功率、辐射天线等技术的迅速发展,IEMI干扰源的设计门槛不断降低,相关犯罪案件、恐怖活动、军事应用时有报导,引发了学界对关键设备IEMI抗扰度的广泛关注[5-8]。

为定量化评价受扰设备在辐射电磁环境下的损伤性,前人基于对大量效应试验的总结归纳,发现了电子设备电磁损伤程度同其响应波形范数间的强相关性,由此发展了基于范数的设备抗扰度量化表征评价体系[9-12]。具体而言,针对响应波形f的p范数定义为

(1)

表1 响应波形f的p范数、对应的物理含义及效应现象Table 1 p-norm of measurement f,the associated physical quantity and possible susceptibility effect

上述针对HEMP、UWB、HPM等电磁环境的典型设备抗扰度研究建立在明确辐射场时域波形的基础之上,然而,IEMI人为制造的特点决定了其波形更为随机、智能,设计者可利用多种技术,产生不同波形的IEMI(例如,不同频段窄带脉冲、双指数脉冲、高斯脉冲、正弦衰减波等)[18]。不同辐射IEMI波形作用于电子设备的耦合效率差异巨大,难以通过穷举所有可能波形的方法评定系统的响应范数。

为克服辐射波形随机多变给设备IEMI抗扰度评定带来的挑战。作者在前序研究中提出了在约束IEMI辐射能量密度的条件下,视其波形为连续随机变量,优化研究任意可能波形IEMI作用下受扰设备响应范数的上确界(损伤程度最大的情况),以此表征设备IEMI抗扰度。该思路体现了对设备受IEMI辐照最极端情况的分析,适用于对电磁安全性具有较高要求的电子设备。依照该思路,前期对整流冲击(1范数)、能量(2范数)及峰值(∞范数)的范数定界问题进行了研究[19-22],发现IEMI辐照下系统响应的1范数不存在上确界,窄带脉冲作用下会发散至无穷;2范数上确界在IEMI为调谐窄带波形时可获得,其大小由系统耦合效率函数谐振峰值决定;波形峰值范数(∞范数)在IEMI频谱同系统耦合效率函数共轭匹配时达到最大,表现为复杂的时域宽带波形。对比表1可知,尚缺失针对斜率峰值、冲击峰值的范数定界分析,对∞范数敏感型目标设备的IEMI抗扰度评定有待深入研究。

由此,为完善IEMI辐照下的设备响应范数定界方法理论体系,本文进一步研究了针对斜率峰值、冲击峰值的上确界评定问题,通过构建泛函优化问题,研究对设备最具毁伤能力的入射场波形特征,补全了面向∞范数敏感型设备的IEMI抗扰度评估方法。建立了IEMI辐照设备模型,通过构建并求解等效最优化问题,获得了∞范数上确界解析解;将方法应用于Vivaldi天线及对数周期天线(LPDA)两类超宽带天线,对比分析了最大化斜率峰值、冲击峰值的IEMI波形特征,研究了范数上确界评定方法的准确性。

1 IEMI辐照下设备∞范数定界方法

1.1 IEMI辐照电子设备模型

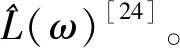
(2)

1.2 峰值范数上确界评定结论

(3)

以波形峰值∞范数为最大化目标,可将IEMI最优波形辨识等价为以下优化问题

(4)

式中tp为波形达到峰值的时刻。文献[5]利用拉格朗日乘子法获得了该问题的最优解析解,即

(5)

(6)

1.3 斜率峰值范数上确界评定

(7)

(8)

(9)

(10)

式(9)中等号成立的条件是存在常数C1,使得

(11)

联立式(10)和(11),可求得常数为

(12)

由此,可求得问题式(8)的最优解析解为

(13)

VL(t)=

(14)

(15)

1.4 冲击峰值上确界评定

(16)

由傅里叶变换性质可知

(17)

(18)

Hilbert空间中,由Cauchy-Schwarz不等式可知,电压波形的冲击峰值满足

(19)

式(19)中等号成立的条件是存在常数C2,使得

(20)

式(20)同约束条件式(10)联立,可得常数C2应满足

(21)

代入式(20)可得所辨识的IEMI最优波形频谱及其负载响应电压波形分别为

(22)

VL(t)=

(23)

(24)

2 针对超宽带天线目标的∞范数定界问题

本节选取了Vivaldi及LPDA两类超宽带天线作为受扰电子设备[25-26],利用所提范数定界方法,分析了IEMI辐照受扰天线的极端情况,对比讨论了不同范数目标下IEMI最优波形的时频域特征。

2.1 受扰天线宽带耦合效率

Vivaldi、LPDA天线均为典型的超宽带天线,基于PCB技术设计的两类受扰超宽带天线结构如图2所示。选用FR-4环氧玻璃布层压板(相对介电常数为4.3,介质损耗角正切为0.025)作为PCB基板材料,基材厚度ts=2 mm,天线贴片及微带馈线分别位于基板两侧,材质均为厚度tt=38 μm、电导率为58 MS/m的退火纯铜。

如图2(a)所示,Vivaldi天线总长度la=41 mm,宽度2lb+s=30 mm。天线开口按照指数函数变化规律延伸至基板末端,贴片层关于y轴对称,其中lb=14.5 mm,le=31 mm。其他微带馈线结构参数为lf=5 mm,ld=3 mm,lp=20 mm。LPDA天线由10根上下两层交错布放的阵子组成,结构如图2(b)所示,由馈源端至远端,将阵子由1～10编号,则阵子长度lo1～lo10分别为[3.34,4.08,4.98,6.08,7.41,9.04,11.02,13.45,16.40,20.00] mm;宽度wo1～wo10分别为[0.57,0.69,0.84,1.03,1.26,1.54,1.87,2.29,2.79,3.40] mm;间距分别为[11.97,2.05,2.50,3.05,3.71,4.53,5.53,6.74,8.19,10.03] mm。天线长度lc=70 mm,总宽度ld=50 mm;wf=1 mm。

2.2 IEMI辐射波形及天线端口响应波形的时、频域特征分析

假设IEMI是频谱能量分布在[3 GHz,6 GHz]内的任意波形平面电磁场干扰,辐射场的能量密度不超过WE=1 mJ/m2。考虑最大化负载波形的斜率峰值、冲击峰值两种情况,假设相应范数均在t=td=ti=10 ns时达到最大。由式(13)、式(22)可分别计算两种极端耦合情况下所需施加的IEMI最优波形频谱,结果如图4所示。

利用逆傅里叶变换,可进一步获得最优IEMI电场分量的时域波形,结果如图5所示,为突出波形的细节差异,仅绘制了[8,12] ns内的电场波形,可见,IEMI最优时域波形并非双指数、高斯等常见简单波形,而是不断振荡衰减的双极性复杂波形,针对Vivaldi及LPDA天线的最优IEMI波形十分相似,但是细节上存在差异,大多能量集中于2～3个振荡周期内,波形幅值约为45 kV/m。若考虑不同能量密度约束WE,仅需等比例增减辐射场幅值,无需改变具体时域波形的细节特征。

将图4、图5中给出的波形作为IEMI激励场,辐照受扰Vivaldi天线,可得到天线负载上感应电压时域波形如图6所示。针对同一天线,斜率峰值/冲击峰值最优波形所感应的响应电压均相对于极值时刻t=10 ns奇对称,且该时刻对应电压波形的过零点。由于LPDA耦合效率高于Vivaldi天线,可发现响应波形的幅值及对应∞范数也明显增加。

3 范数上确界最优性验证

为验证上述IEMI最优波形具备对受扰天线的最强损伤能力,可用于极端条件下的设备IEMI辐照抗扰度的量化表征。本节选取了均匀频谱波形、宽带高斯波形、窄带高斯波形3种典型IEMI环境作为辐射激励场,通过对比典型IEMI波形及最优波形作用下的负载电压响应波形及其范数,验证方法的最优性。选取的3种典型IEMI电场频谱分布如图7所示,其能量密度均归一化至约束条件,即WE=1 mJ/m2。

具体而言,均匀频谱波形在[3 GHz,6 GHz]频段内的幅值完全相同,相位均为0;宽带高斯波形服从文献[24]中定义,为减小频谱泄漏的影响,将90%的能量强制约束在所考虑频段内[24];窄带高斯波形中心频谱为系统谐振点fc=5 GHz,带宽比为1.01,其对应的时域波形为快速上升并衰减的正弦波形。