连续综合控制系统的状态反馈广义H2 控制*

孙凤琪

（吉林师范大学 数学与计算机学院，吉林 四平 136000）

引 言

将最优控制理论应用于工业过程控制领域，就得到了具有广泛工程背景的线性二次型(LQG)控制问题，即 H2控制问题[1-3].广义 H2控制能使一个实际控制系统，在含有不确定性和时变时滞的情况下保持渐近稳定，并且满足 L2-L∞性能指标要求.以系统的二范数为性能指标的广义 H2控制理论，可以获得较好的动态、稳态性能，是现代控制理论的一个重要分支.其源于可运用一套完整的、系统化的方法来探究非线性系统的稳定性以及控制器设计问题[4-7]，可以切实地处理系统在控制领域内存在的某些不足，已经发展成为解决非线性不确定系统的一个有力工具.目前已成功应用于通讯、网络控制、工业生产过程及航空航天等社会发展的各个领域.

近年来，有很多学者对此做过深入研究[5-8]. 文献[2，9-10]讨论了时滞神经网络系统广义 H2滤波器设计问题，采用线性矩阵不等式技术推导了此类不确定系统的鲁棒 L2-L∞状态反馈控制器存在的充分条件，但所得结果与时滞大小无关，当应用于小时滞系统时将具有较大的保守性. 文献[11]研究了一类离散状态半Markov跳变线性系统的异步广义 H2控制问题，引入弱无穷小算子、松弛变量给出了等效条件， 并设计了异步控制器. 但无穷小算子技术的引入带来了计算上复杂度的增加. 文献[12]主要讨论了连续时间非线性系统的广义 H2控制问题，得到了该类非线性系统存在鲁棒 H2模糊控制器的充分性条件，但时滞的上界选取较大的数时， 得到的稳定性判据并不适用.文献[13]研究了一类随机中立型时滞系统的广义 H2控制，得出了随机中立型时滞系统广义 H2控制器的具体构造方法，但系统中并未涉及摄动问题，导致系统含有多个时标时并不适用.

鉴于此，本文将研究一类带有时变时滞奇异摄动连续不确定性的综合控制系统的广义 H2控制问题，采用线性矩阵不等式方法，构造适当的Lyapunov泛函，并结合相关引理，推出 H2控制器的具体设计方法，并使得闭环系统在满足一定的性能指标前提下渐近稳定.

引理1[14]对于适当维数的矩阵 E1, D1, E2, D2，对称矩阵Y，不确定性矩阵 F(t)满足 FT(t)F(t)≤I ，则

的充分必要条件是存在正常数 η＞0, γ ＞0，使得

引理2[14]若 X, Y 为向量，则文献[14]的引理2.3变为

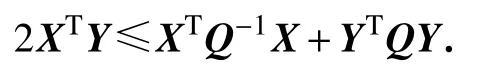
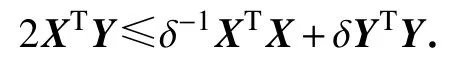
1 问 题 描 述

考虑如下带有控制输入和干扰输入的连续不确定时变时滞奇异摄动控制系统：

这里τ和µ是已知实常数； φ(t)是连续向量初始值函数； F(t)∈Ri×j是范数有界的不确定系统模型参数矩阵，具有如下范数有界不确定性结构：

首先，设计记忆状态反馈控制器为

其中， K,K1是待定的控制器增益矩阵.将式(4)代入原系统(1)，则闭环系统成为

其中

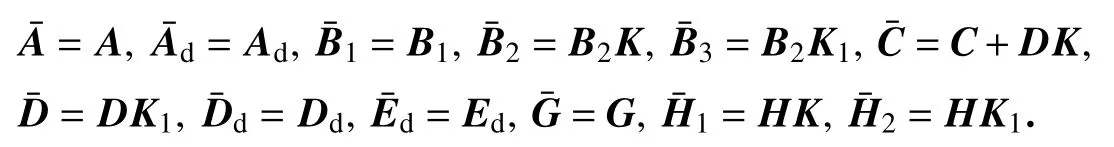
针对系统(1)设计形如式(4)的状态反馈控制器，对给定的标量，设计状态反馈控制器(4)，使得连续不确定时变时滞奇异摄动闭环系统(5)渐近稳定，且满足如下性能：

2 广义 H2控制定理

2.1 时滞依赖情形

定理1 给定正数 ε¯＞0， γ＞0，对满足条件(2)和(3)的闭环系统(5)以及 L2-L∞性能指标，若存在对称正定矩阵 Q＞0， M＞0， P＞0，矩阵 Zi(i = 1, 2,···, 5)且 Zi=(i = 1, 2, 3, 4)，下列LMIs条件是可行的：

其中

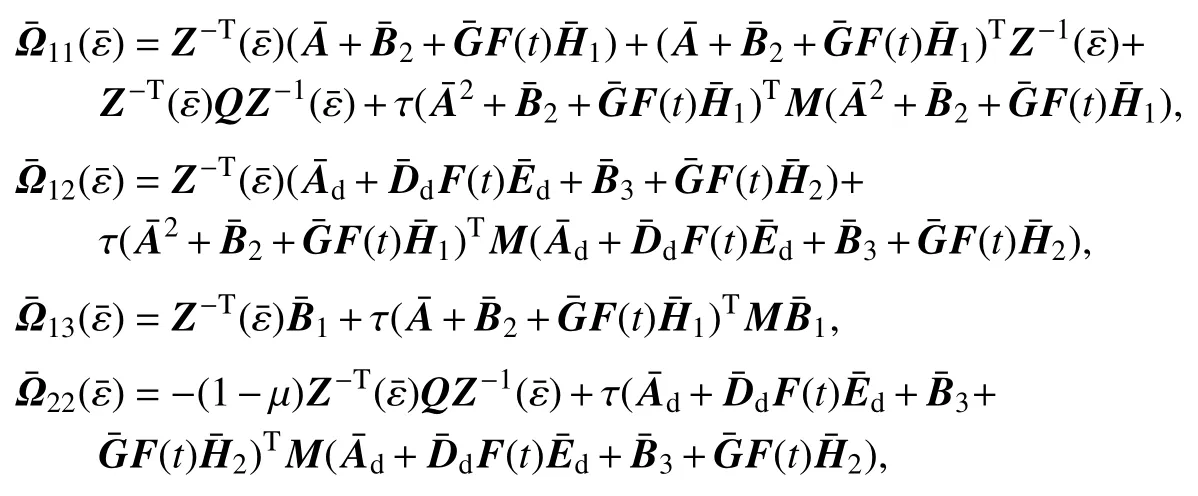
证明首先建立闭环系统(5)在时的渐近稳定性.定义一个二次L-K泛函V(x(t)) = V1(x(t))+ V2(x(t))+V3(x(t))，其中

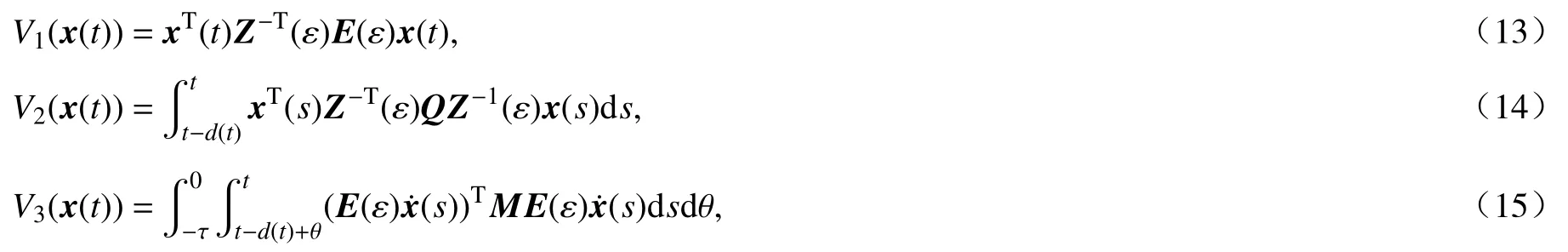
由矩阵不等式条件(6) ~ (8)及文献[14]的引理4.2，推得

则

故

则 V(x(t))为正定的L-K泛函.

根据文献[14]的引理4.3，可知矩阵不等式条件(9)、(10)蕴含下式：

其中

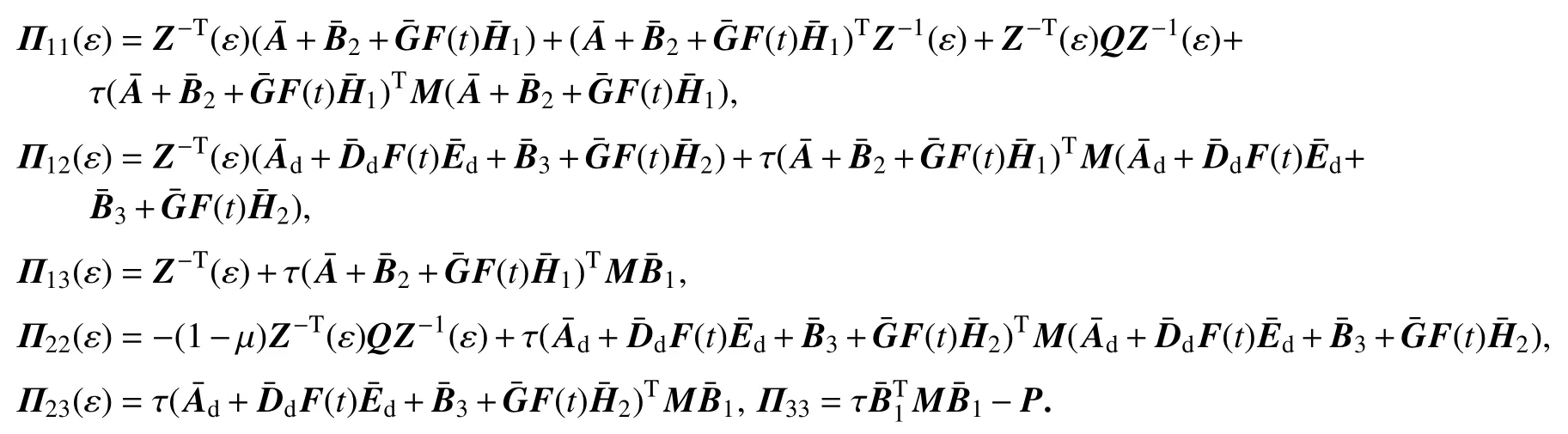
其中

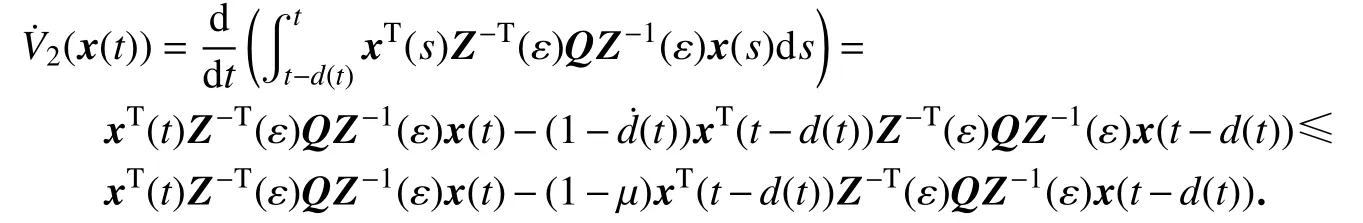
进而

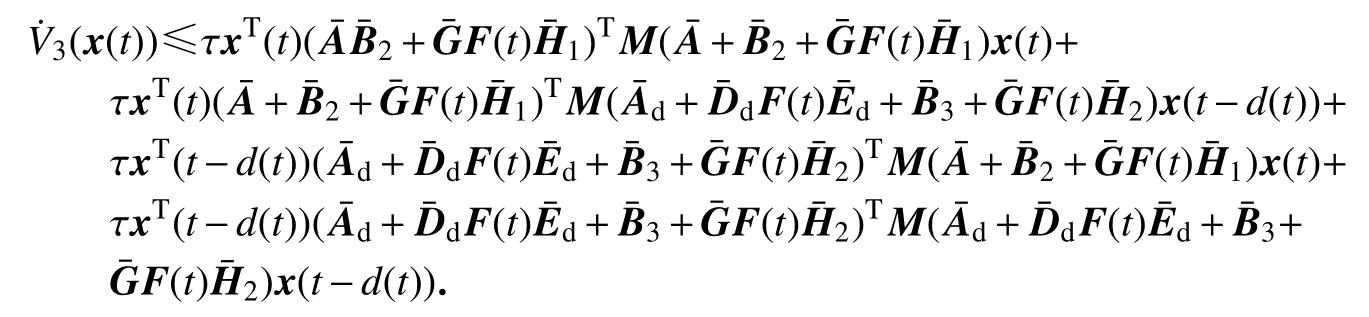
所以

其中

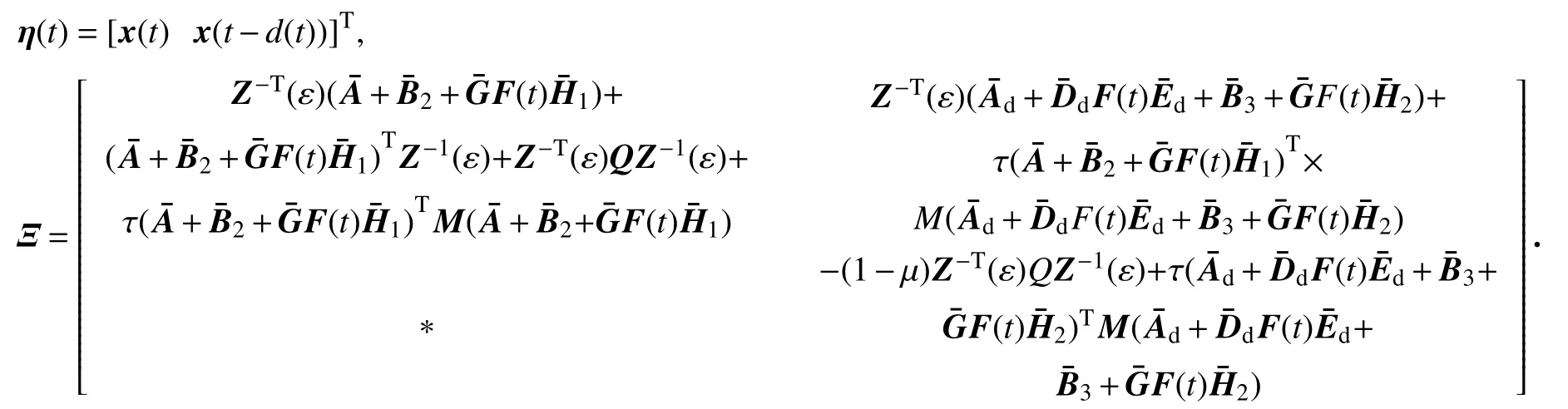
从式(16)可知 Ξ＜0，故推出 ηT(t)Ξη(t)＜0，于是在 ω(t)≡0时，(x(t))＜0.由Lyapunov稳定条件可知，闭环系统(5)是渐近稳定的， ∀ε∈(0,ε¯].

为了建立闭环系统(5)的 L2-L∞性能准则,假设零初始条件，即 V(x(t))|t=0= 0，构造新的性能指标如下：

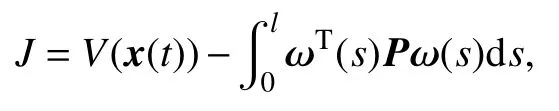
其中P为待定的对称正定加权矩阵，则对于任意的非零 ω(s)∈L2(0,∞]及 t≥0，有

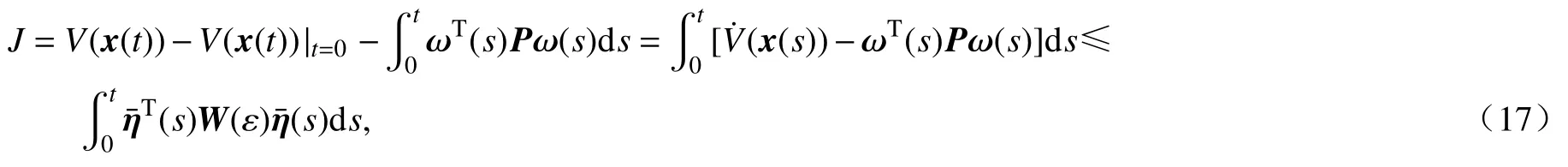
其中

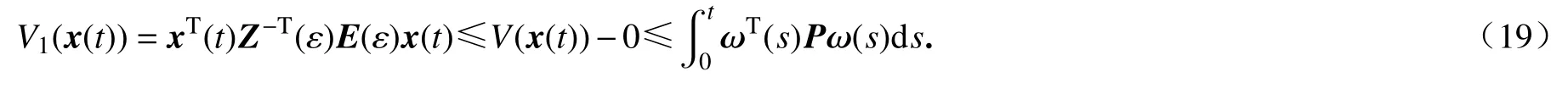
另一方面，由Schur补引理可知，式(9)等价于

式(10)等价于

由式(19)、(20)可得

对所有的 t≥0取最大值，则对于任意的非零 ω(t)∈L2[0,∞)，有

其中

定理1得出了闭环统满足 L2-L∞性能指标的广义 H2控制器成立的条件，但是控制器的参数是未知的，上式关于变量K，K1，M，P，Q和 Z(ε)是非线性的，进行线性化处理，即得如下定理，具体推证略.

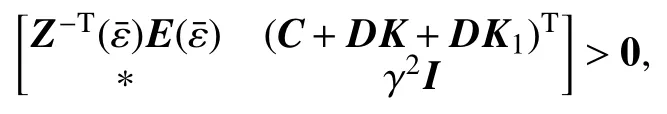
其中

注1 系统控制器亦可以设计成输出状态反馈控制器，理论推导均与定理1方法类似，同时也可以推广到无限时滞情形，此略.

2.2 时滞独立情形

其中

证略.

详略.

3 算 例

考虑如下带有控制输入和干扰输入的时变时滞不确定控制系统：

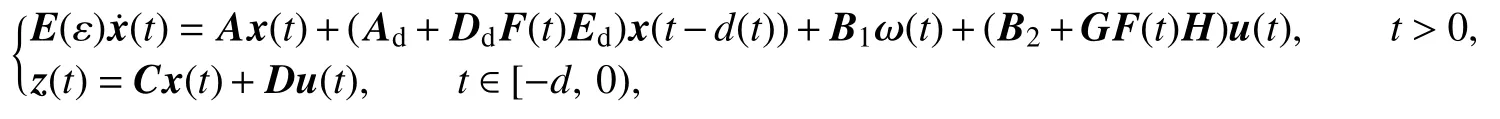
其中

给定 γ= 1.5，应用定理2可得该系统的记忆状态反馈控制 u(t) = Kx(t)+K1x(t -d(t))，其中求解LMIs，最优值完全符合设计要求.

由表1知，定理2所给的控制器存在，并且具有较大的奇异摄动参数上界值0.35，同时广义控制区间在(0，0.35]区间内，大于文献[12]的(0，0.3]，扩大了闭环系统的渐近稳定范围，最优性能指标1.1265也相对更小.验证了本文所得结论的有效性和可行性，得到的控制器比文献[12]控制效果更具有一定的优越性，并且适用于标准和非标准情形.

表 1 广义H2稳定性能指标对比Table 1 Comparison of generalized H2 stability performance indicators

4 结 语

1) 本文引入新的广义 H2性能指标的定义，选取新的依赖于时滞和摄动参数的二次型Lyapunov泛函. 同时借助新的引理及交叉项界定方法，对记忆情形推出在时滞依赖和时滞独立两种情况下的系统广义稳定的充分性判据， 且在 (0,]区间内，扩大了稳定界，使记忆状态反馈广义 H2控制器具有更小的保守性.

2) 本文研究了状态反馈广义 H2控制问题，如何将结论推广到输出反馈广义控制问题中，还有待进一步探讨.

3) 若加深理论高度，将连续奇异摄动系统拓展到离散奇异摄动系统，怎样将连续奇异摄动系统广义 H2控制理论应用到离散奇异摄动系统中，解决时变时滞离散奇异摄动系统的广义 H2控制问题，这将是一个极具挑战的课题.

4) 在推得时滞依赖和时滞独立相关的稳定性结果的过程中，可以对其中的某一变量作进一步的限定，减小计算量，使过程和结论简单化，这样用较大一点的保守性，换取实际控制系统的简便性，也是一个具有实际意义的理论方向.因篇幅所限，将继续在今后的学习中予以研究.作为一个新的研究领域，广义 H2控制理论仍处于不断改进，不断发展之中[15-18]，在它广泛的工程背景下，无论是理论本身，还是工程的实际应用，都必将会取得更有意义的成果.