变双曲圆弧齿线齿轮切削仿真及参数优化

廖奎，侯力，张海燕，吴阳

(四川大学机械工程学院，四川成都 610065)

0 前言

变双曲圆弧齿线圆柱齿轮(VH-CATT)是一种将圆弧齿线运用于齿轮齿线上的新型齿轮。与现有齿轮形式相比，其承载能力更强、传动性能更优，具有广阔的运用前景。VH-CATT由曲线齿锥齿轮衍生而来。20世纪初，由于普通渐开线齿轮普遍有着承载能力差的缺点，美国韦尔哈德最早提出将齿廓发展为圆弧形，并在曲线齿锥齿轮的研制中取得了较大成功。LITVIN和GUTMAN对该曲线齿锥齿轮的成形理论及接触进行了深入研究。而在国内，随着我国社会的不断发展，实际机械工程对于齿轮的要求也越来越高，更多的科研工作者开始关注弧齿轮这一具有前景的研究方向，如吉林大学彭福华教授曾尝试通过圆拉法提高弧齿圆柱齿轮的加工效率；曾韬等数学工作者对螺旋锥齿轮的啮合理论进行了系统的研究等。

VH-CATT由于成形复杂，很难用普通的数控机床加工成形，所以需要使用高档数控机床进行加工。但是这样加工出来的VH-CATT为近似加工，存在有加工原理误差、成本极高、很难工业化等缺点。因此，要实现VH-CATT的大规模工业化，其专用数控机床的研制就显得格外重要。由于现在没有专用的加工机床，其加工以及调整较为复杂。如果不对VH-CATT切削加工过程中的参数进行合理设置，就不易获得理想的加工效率及加工质量。因此，本文作者分析VH-CATT的加工原理，进行VH-CATT的切削仿真并利用鲸鱼算法优化切削参数。

1 VH-CATT切削加工成形原理

与传统的圆柱齿轮相比，VH-CATT的齿线特殊，沿着与齿轮同轴的某一圆柱面展开的平面上呈圆弧形，而其他齿轮如直齿轮、斜齿轮等的齿线为直线与斜直线。VH-CATT传动是较优的一种新型传动方式。

如图1所示，VH-CATT的啮合齿线为空间曲线。从齿轮端面上看，在中间截面上其轮齿为渐开线齿廓，其余截面上均为变双曲齿廓。VH-CATT的啮合接触线较同大小的直齿圆柱齿轮更长；齿面形状为拱形，由凹面和凸面组成。因此，从理论上讲，VH-CATT拥有更好的承载能力、传动平稳性、疲劳强度。

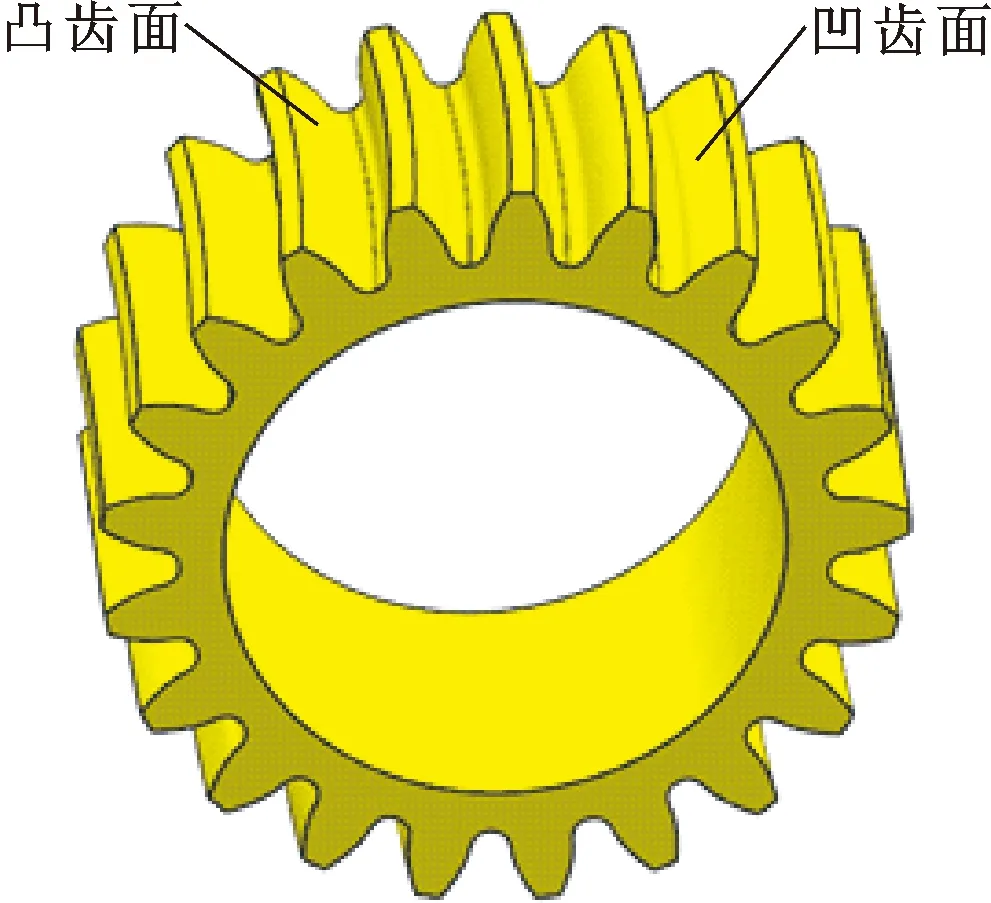
图1 齿轮轴侧图

如图2所示，VH-CATT旋转加工刀盘加工该齿轮过程中，刀盘沿轴的高速旋转加工是齿轮铣削过程中的主运动，在刀盘做旋转运动的同时，齿坯在平面做范成运动。这个运动为齿轮铣削过程中的进给运动，即齿坯沿着轴的水平运动与齿坯绕着轴的旋转运动。加工完一个齿槽后，齿坯沿着轴移动回到初始位置，齿坯绕着旋转分度，然后加工齿轮的下一个齿槽，直至整个VH-CATT齿面加工完成。

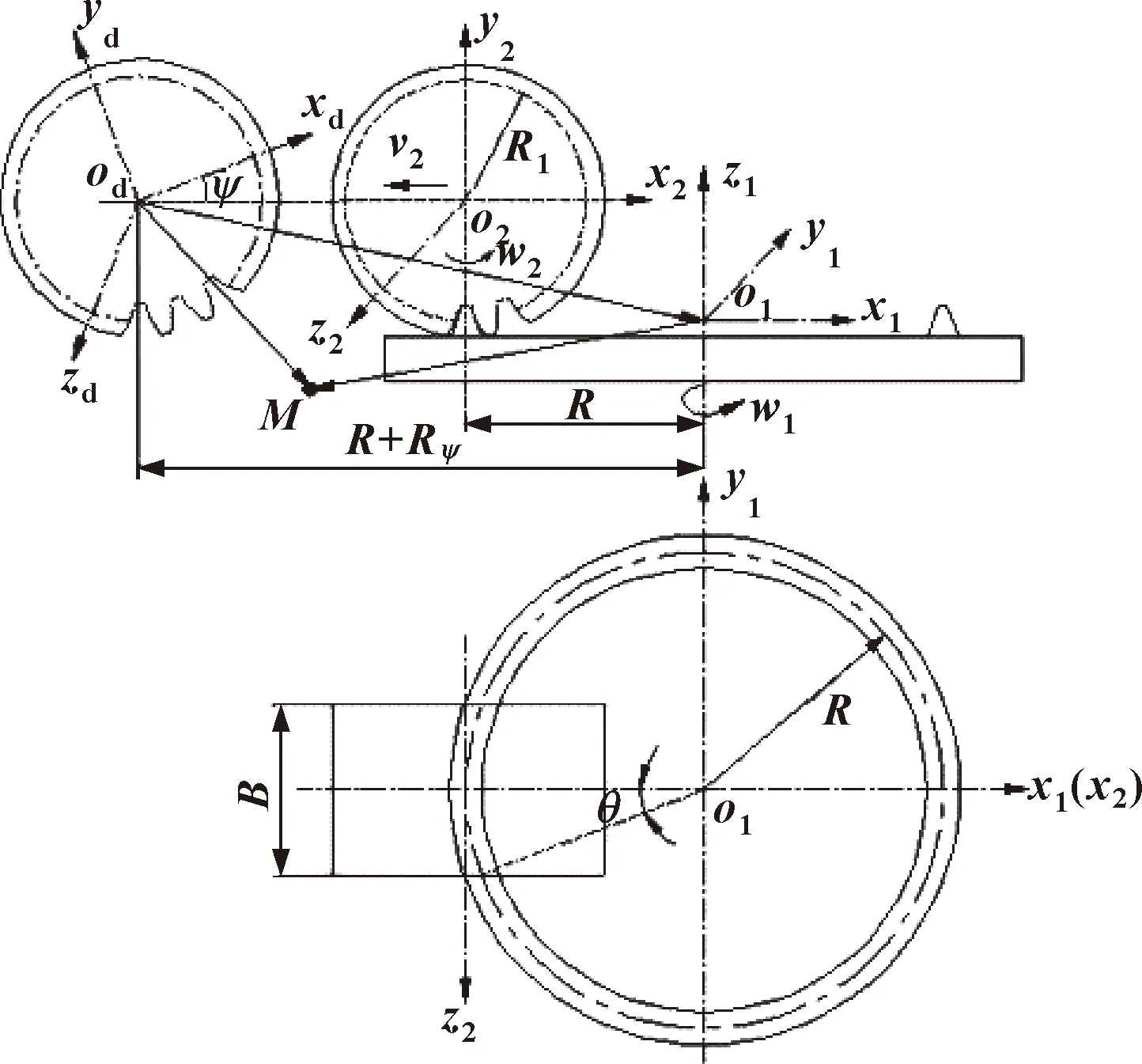
图2 加工原理

2 VH-CATT切削模拟仿真

使用有限元模拟方法分析齿轮实际加工情况，可以分析刀具在实际加工过程中的作用力以及刀具其他特定切削性能的变化。通过分析不同切削参数下的切削力，综合考虑切削参数对切削结果的影响。

对加工过程进行详尽的模拟十分复杂，所以有必要对加工模型进行简化。由于齿轮各个齿槽的切削过程相同，只需要完成一段齿面的仿真加工。而所要加工的变双曲圆弧齿轮的齿廓弧线曲率半径较大，所以可以在仿真时将工件作近似的直线处理并以长方体代替，如图3所示。

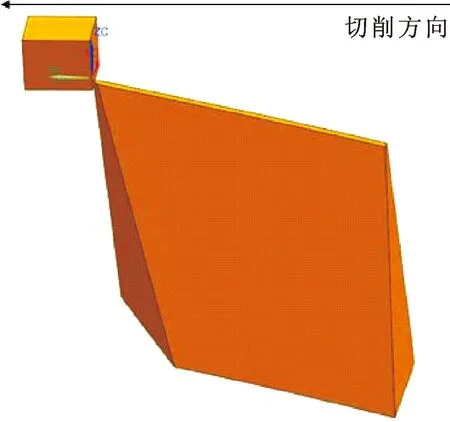
图3 切削近似处理模型

材料的本构关系对于有限元仿真十分关键，因为它一定程度上代表了材料的本质属性。在此类型的仿真中，Johnson-Cook模型对金属的力学行为具有很好的拟合性以及数值稳定性，可以方便地应用于有限元分析模型中。因此，本文作者采用Johnson-Cook模型，并将工件材料设置为45钢，材料参数及其本构模型参数如表1—表3所示，将刀具材料设置为WC(碳化钨)材料。在仿真过程中，为提高切削效率，将刀具设置为刚体模型。

表1 材料参数

表2 45钢J-C模型参数

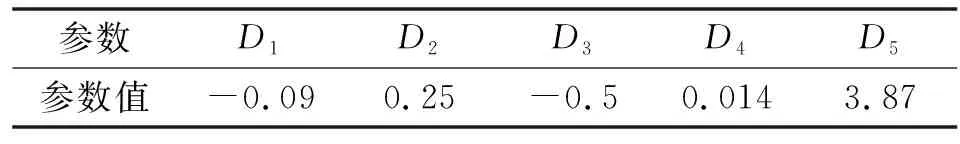
表3 45号钢J-C 模型失效参数

设置材料模块、分析步等模块后，当模拟仿真完成后，由ABAQUS软件的结果模块中能够观看铣刀条切削过程中每一个时刻的模拟仿真，并且能够获得模拟仿真输出的结果，如图4所示。

图4 铣刀切削仿真

3 仿真切削参数优化

3.1 鲸鱼优化算法

鲸鱼优化算法(Whale Optimization Algorithm，WOA)是模仿座头鲸的狩猎行为提出的一种新型启发式优化算法。目前的鲸鱼算法与其他群优化算法相比，主要区别在于：它采用随机或最佳搜索代理来模拟捕猎行为，并使用螺旋线来模拟座头鲸的泡泡网攻击机制。在WOA 算法中，种群内的每一只鲸鱼所在的位置都是一个可行的解，这样鲸鱼群就可以包围猎物并捕捉。

由于最优设计在搜索空间中的位置不是先验已知的，WOA算法假定当前的最佳候选解是目标猎物或接近最优解。在定义了最佳搜索代理后，其他搜索代理将尝试向最佳搜索代理更新它们的位置。捕食过程用数学表达式表示为

(1)围困猎物

(+1)=()-

(1)

=|()-()|

(2)

式中：()为当前群体最优位置；、为系数；为当前鲸鱼个体与最优位置之间的距离。

其中、的计算方式如下：

=2-

(3)

=2

(4)

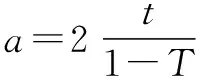
(2)发泡网攻击

首先是对猎物进行收缩包围，这个过程依靠降低值实现，其位置更新按照公式(5)进行，并在接下来的时间内按照螺旋线公式更新位置，其表达式为

(+1)=′cos(2π)+()

(5)

式中：′=|()-()|是当前情况下的鲸鱼最优位置与鲸鱼个体之间的距离；为对数螺旋形状常数；是-1～1之间的随机数。

(3)随机搜索

(+1)=(+1)-

(6)

=|()-()|

(7)

式中：()表示当前情况下随机一个个体的位置。

3.2 模型设计变量

一般情况下，在整个加工过程中，将对切削过程影响较大的变量作为设计变量,对优化结果起不到重大作用的变量通常作为常数。一定的简化处理对于模型来说是必要的，若使用太多的变量，可能会使计算求解的过程变得异常复杂，增加一些不必要的工作，增加难度。在VH-CATT加工过程中，使用必要的切削参数条件作为优化变量，包括：主轴转速(r/min)，每齿进给量(mm)，切削深度(mm)。

3.3 目标函数

本文作者旨在获得较小的切削力和较高的加工效率，因此选取单件加工时间和切削力作为优化目标。

3.3.1 单件加工时间

单齿槽加工基本时间为

=2++

(8)

式中：为单齿槽加工基本时间(min)；为齿坯回转时间(min)；为切入齿坯时间(min)；为工进、工退时间(min)。

齿槽加工如图5所示。

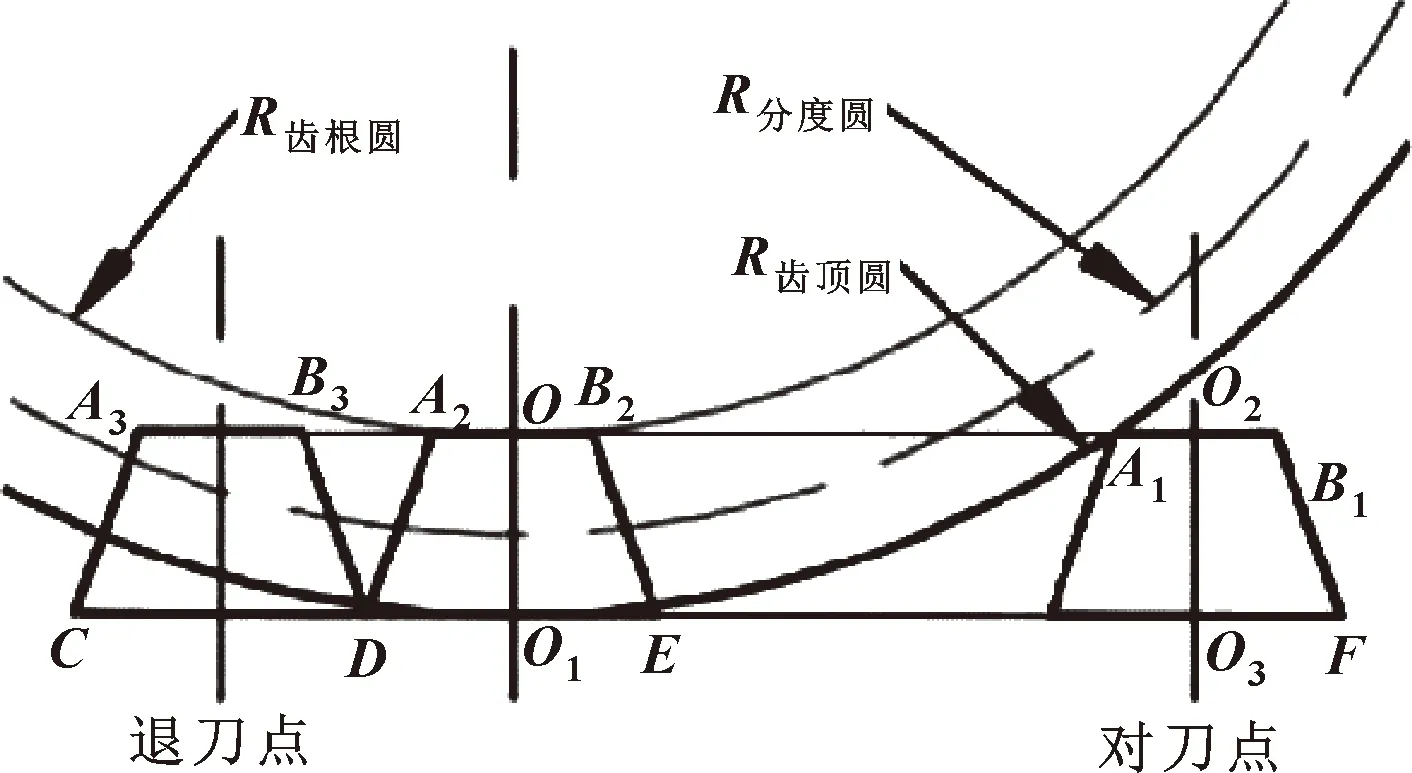
图5 齿槽加工示意[11]

由图5可得:

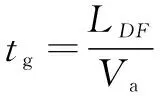
(9)

式中：

=+++

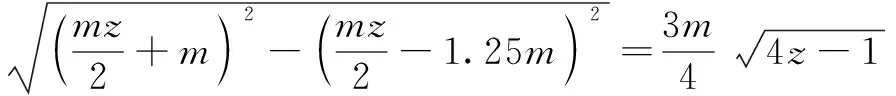
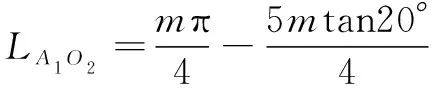
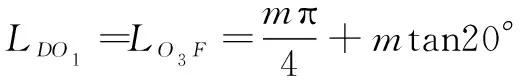
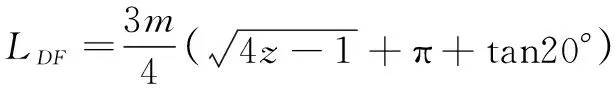
(10)

=

(11)

式中:为铣刀齿数。对于任意一个齿槽加工，设加工步长为，相应地，齿坯在轴方向上的运动距离为:

(12)

则一个齿槽加工过程中总的切削刀数为

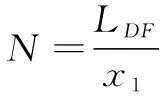
(13)

在实际加工过程中，取正整数，所以文中对进行取整。

一个齿槽加工完成以后，开始加工下一个齿槽前需要重新对刀。重新对刀时，齿坯只需要在轴方向后退，同时绕轴旋转：

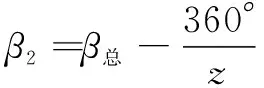
(14)

=

(15)

则：

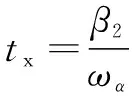
(16)

式中：为分度角速度。

单件加工基本时间为

=

(17)

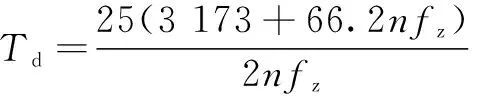
(18)

3.3.2 切削力函数建模

切削力与铣削参数之间的关系没有明确的表达公式，本文作者使用指数公式对切削力进行模拟。若在进行模拟试验时，将所有的试验遍历，会损耗许多不必要的时间与精力，所以本文作者使用三因素三水平正交试验法来提高试验的效率。

正交试验选取的参考因素为主轴转速(r/min)、切削每齿进给量(mm)、切削深度(mm)，表4所示为正交试验的因素水平及仿真试验结果。

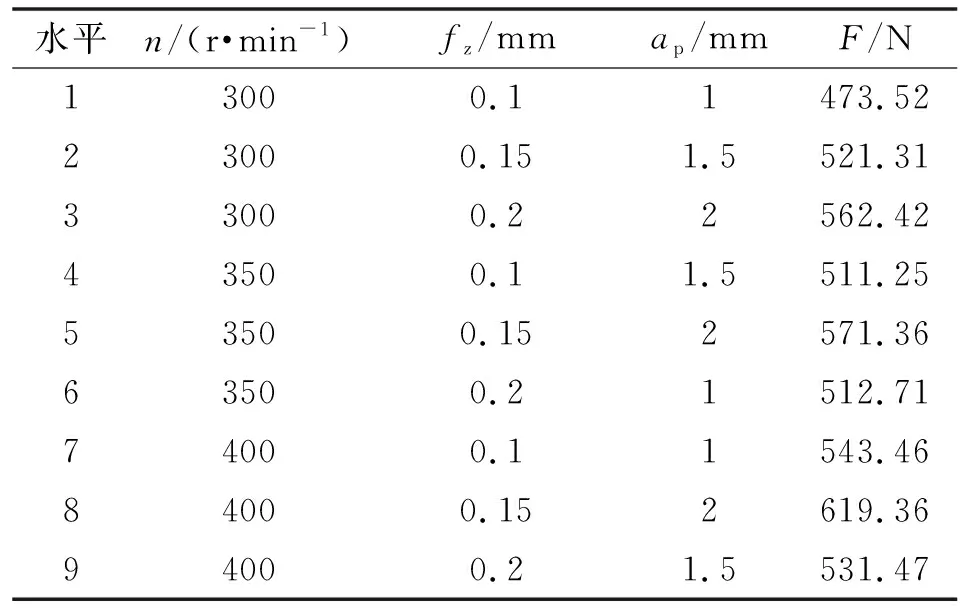
表4 仿真试验结果

设置切削力的经验模型为

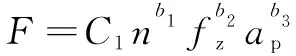
(19)

其中：为经验修正系数；、、为影响因素；为切削力。

对模型公式取对数得：

lg=lg+lg+lg+lg

令上式中lg=、lg=、lg=，lg=、lg=，则经验模型的线性方程为

由上文分析可知，各变量对于水资源消耗影响的动态效应存在着省域差异，为了进一步探讨城镇化各因素对水资源消耗影响的区域差异，本文将我国30个省份按照国家统计局地区划分［22］的方法分为东北、东部、中部、西部4个区域，研究区域的划分及所包含省份见表5。

=+++

(20)

通过仿真数据建立经验模型的多元线性回归方程组可表示成矩阵形式：

=+

其中:

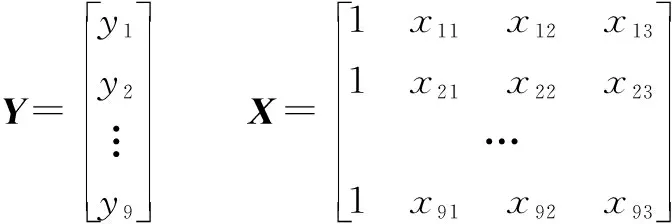
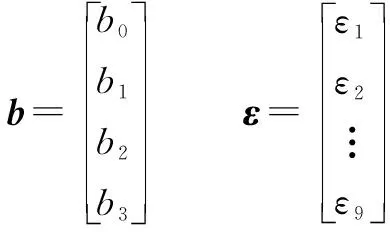
采用最小二乘法估计，设、、、为、、、的最小二乘估计，所以回归方程为

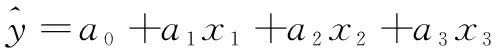
(21)

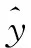
多元性线性方程组参数的最小二乘估计矩阵为

=()

(22)

式中：为的转置矩阵;()为的逆矩阵。

通过Origin软件对试验数据进行拟合，并利用MATLAB软件对其运算进行检验，获得多元线性回归方程的系数，得到影响切削力的转速、进给量和切深的优化模型：

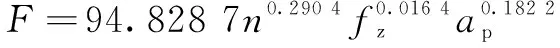
(23)

通过进一步计算，可以算出残差平方和即剩余平方和，记为。

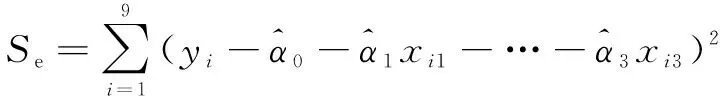
所以有：

=-α

(24)

经计算得出=0.021，越小说明回归方程表达变量之间统计相关关系的精确程度越高，回归分析的效果越好。

经拟合回归得到变量与优化模型之间的函数关系后，需对其进行显著性检验。常用的显著性检验方法有检验和检验，二者在本质上是一样的，文中选用检验法。统计变量为

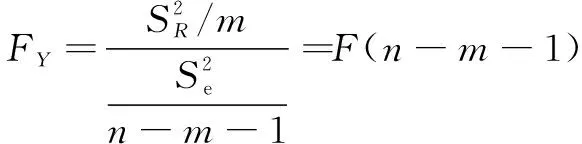
(25)

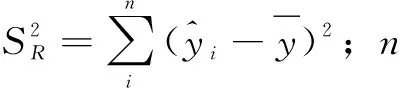
分析利用Origin计算得到的切削力方差表，可以得到方差分析统计量，包括均方误差、自由度、显著水平等，如表5所示。

表5 方差统计结果

假设显著性水平=0.05，查表可知>095(38)=882，且<0.01，由此可知所得到的优化模型与变量之间具有良好的函数关系。

3.3.3 函数确定

对于具有多个目标函数的优化问题，一直较难解决，很难得到满足多个目标的最优解。一般将多目标转换为单目标优化，常用的方法有两种，一种是加权求和法，另外一种是引入一个极大熵函数来对其进行简化。本文作者采用加权求和法，简化以后所对应的单目标优化函数为

min(,,)=min(+)

(26)

式中：、为权重，且+=1。

利用专家打分法或层次分析法等对权重进行确定，得到两个量纲不同的目标函数。因此，需进行量纲归一化处理：

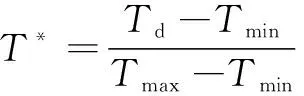
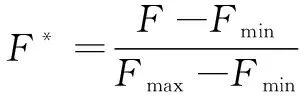
式中：、分别为单目标函数优化的最大值与最小值；、分别为单目标函数优化的最大值与最小值。

最终得到的单目标优化函数为

min(,,)=min(+)

(27)

3.4 约束条件

优化设计选择变量的设置并不是任意的，必须对它进行一定约束。机床铣削加工参数选择在满足加工工艺要求、机床条件等基础上建立约束条件，使优化结果更符合实际加工要求。决策变量应满足以下约束条件。

(1)主轴转速约束条件：<<，其中为机床最低主轴转速，为机床最高主轴转速。

(2)每齿进给量约束条件：<<，其中为机床最低进给量，为机床最高进给量。

(3)刀具对切削的约束条件。切削深度的增加可能造成刀具的折损，所以刀具的切削深度不能大于刀具的最大切深，即0<<，其中为刀具的最大切深，单位为mm。

3.5 优化结果与分析

利用MATLAB进行鲸鱼算法的编程，对齿轮加工过程中的切削参数进行优化，设置最大迭代次数为500、搜索代理数为30。

算法开始运行后，鲸鱼会开始在区域内进行捕食，每一次迭代位置更新，都会向最优值靠近，最后得到的最优位置就是期望得到的结果。由图6可以看出，在迭代近200次后接近收敛。优化后的结果如表6所示。

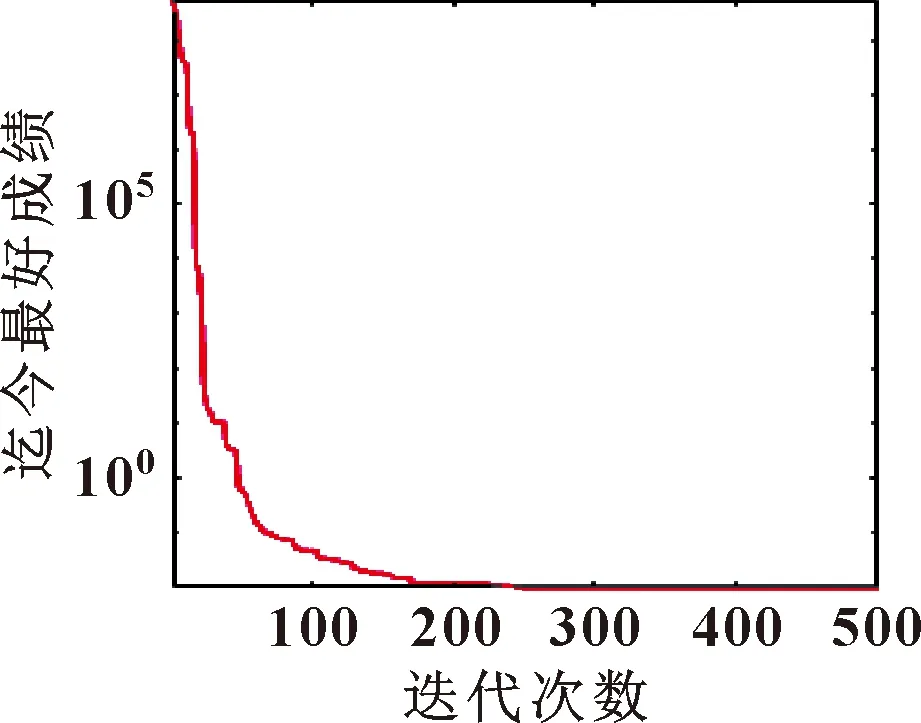
图6 WOA迭代收敛结果

表6 优化结果

4 结论

(1)本文作者分析了变双曲圆弧齿线圆柱齿轮的成形原理及加工过程，利用ABAQUS完成了其切削加工过程的模拟仿真。

(2)根据模拟仿真得到的试验数据建立了切削力的预测模型，通过建立回归模型、模型拟合数据与显著性检测等手段，验证了所建切削力预测模型的可靠性，表明在加工齿轮时，利用该模型能够合理选择切削参数。

(3)基于鲸鱼算法，对VH-CATT的加工切削参数优化问题进行了研究，建立了以加工效率与较小切削力为目标的函数优化模型，并通过加权求和法与归一化处理将它转化为单目标函数优化模型，得到优化后的切削参数为主轴转速=189.3 r/min，每齿进给量=0.046 mm，切削深度=1.89 mm。