五轴加工中心空间位置精度衰退分析

2022-09-20张银虎杨庆东彭宝营王鹏家王增新

机床与液压 2022年10期

张银虎，杨庆东，彭宝营，王鹏家，王增新

(1.北京信息科技大学机电工程学院,北京 100192; 2.超同步股份有限公司，北京 101500)

0 前言

五轴加工中心在复杂曲面加工中占据着不可或缺的地位。复杂曲面的加工精度和五轴加工中心的众多精度指标相关，而每个精度指标对五轴加工中心的性能影响又有很大不同，所以有必要找出这些关键的指标，并分析不同指标所产生的影响，以确定误差的根源，并对加工中心结构的优化设计提供参考。某五轴加工中心运动示意如图1所示。对-五轴加工中心精度保持性进行评价，对于五轴加工中心的生产优化分配、装配过程优化、精度的优化和维护起着至关重要的作用。

图1 某五轴加工中心运动示意

目前，五轴加工中心精度保持性是一个复杂和共性的问题，要考虑五轴加工中心的初始精度和五轴加工精度的衰退状况。虽然在此领域的研究已经较多，并且取得了一定的成果，但是也存在明显的不足。在研究中，首要目标是考虑误差敏感度问题，IBARAKI、邓聪颖、LEE、ANDOLFATTO等深入研究了五轴机床误差问题，并进行了定量分析，在研究过程中采用了不同的方法，包括误差矩阵分析、刚体运动学法等。本文作者采用多体动力学系统理论方法，将各项主要误差传递积累到刀具工作点，建立空间上五轴加工中心的误差模型，并结合全局敏感度分析，以空间位置误差为指标，得到各项误差对加工误差的影响，进而得到关键误差对五轴加工中心空间位置的影响。将各个影响加工精度的五轴精度指标投放到时间维度上，得到相应指标的误差。

1 精度保持性分析

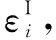
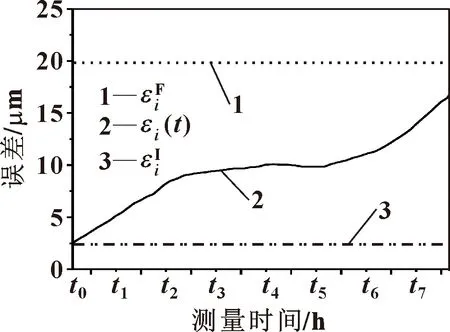
图2 某项精度保持度误差变化特征

五轴加工中心实际使用过程中，使用精度检测仪器对精度指标进行长期测量，获取一定时间节点的离散误差。将精度指标的误差投影映射到时间维度，对其数据进行离散化建模计算，则精度指标在时间内对应的误差变化均值为

(1)

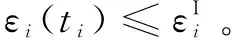
为分析精度保持性能力，将处于时的精度变化静态指标表示为如下形式：

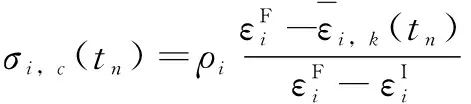
(2)

式中：为条件函数；为五轴加工中心的某项相关指标。

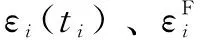
2 精度保持度建模

已知在某个时刻时，理论刀具加工点的坐标是(刀具坐标系)，而实际刀尖工作成形点坐标是(工件坐标系)。如果各坐标系的误差均为0，那么工件上理论刀具成形点和实际刀尖处一致：

(3)

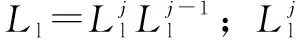
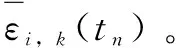
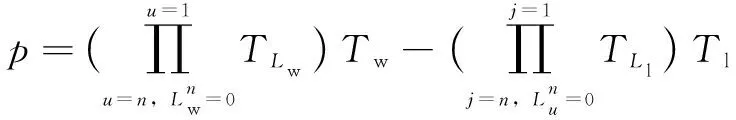
(4)

=[(,,,),(,,,),(,,,)]

(5)

式中：、、分别表示在时间内五轴加工中心在、、轴方向的空间位置某项误差的变化均值。

假设在时间内，五轴加工中心处于、、轴方向的空间位置误差变化均值表示为

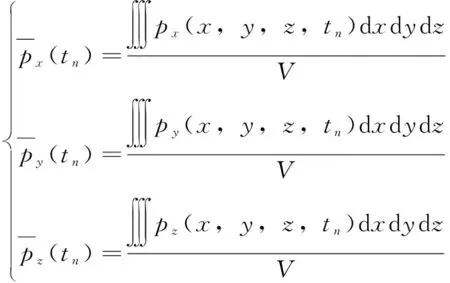
(6)

式中：为刀具与工件接触点的空间行程围成的体积。

进一步，五轴加工中心在、、坐标方向的空间位置精度保持度为

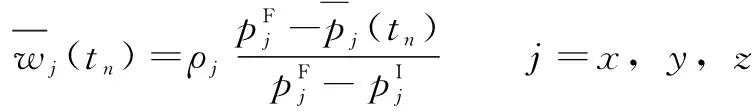
(7)

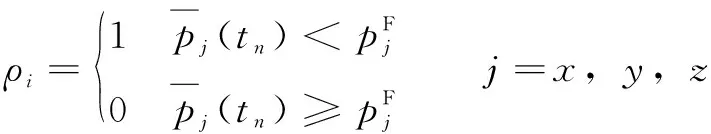
3 关键误差源识别

根据一段时间内精度指标变化特征，分析各精度指标误差变化均值对加工中心空间位置精度保持度的影响。文中主要利用SOBOL全局敏感度分析法。

在敏感度分析过程中需要确定合适的输入量和输出量，其中输入量主要是加工中心项精度指标误差变化均值；而输出量则表示此项精度指标在、、轴方向的空间位置精度保持度。结合公式(7)可以得到：

(8)

式中：代表含有项精度的误差变化均值矢量。

在敏感性分析过程中，对轴方向的空间位置精度保持度进行分析。对应的精度保持度如下所示：

(9)

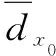
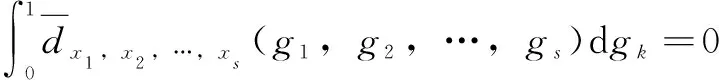
(10)

式中：=1,2,…,。

公式(10)仅有一种分解形式，各阶子项的计算公式如下：

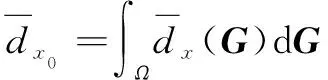
(11)

(12)

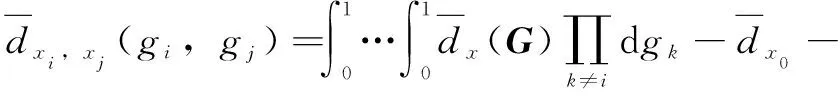
(13)

参照上述公式可以求出其余高阶子项。

根据数理统计原理，模型输出总方差为

(14)

偏方差为

(15)

式中：1≤≤。

对式(10)积分，并代入式(11)，总方差分解为

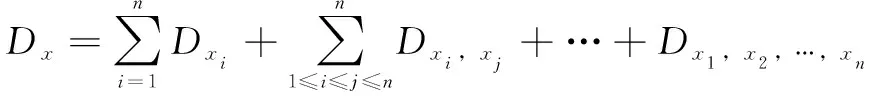
(16)

因此，敏感度表示为

,…,=,…,1≤≤

(17)

根据式(17)有：

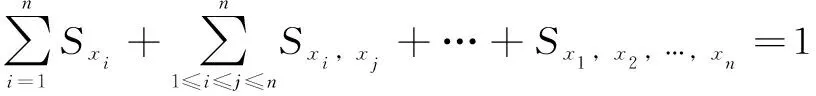
(18)

式中：为在轴方向空间位置精度保持度对于的敏感度；,为在轴方向空间位置精度保持度对于、的敏感度。

采用蒙特卡洛法对参数进行预估：

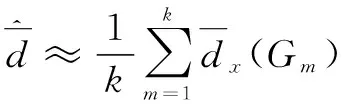
(19)

(20)

(21)

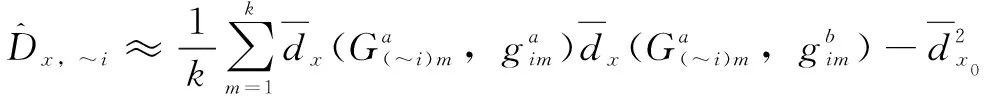
(22)

根据公式(19)—(22)，在轴方向的空间位置精度保持度对于轴的敏感度为

(23)

4 典型实例分析

4.1 五轴加工中心精度长期检测

某-五轴加工中心结构简图如图3所示。从结构上看，该结构主要划分为多个部分，包括转台、主轴以及床身等。在研究过程中，基于ML10激光干涉仪对各误差项进行检测，总计10次，总时间为743天，误差检测项如表1所示。图4主要展示了-轴加工中心误差测量现场。检测结果如表2中所示，主要依据GB/T 17421.1—2016、GB/T 7421.2—2000完成对直线度、定位精度的计算。

图3 某B-C五轴加工中心结构简图

表1 某B-C五轴加工中心误差检测项

图4 B-C轴加工中心误差测量现场

表2 所检测误差数据(部分)

4.2 精度保持性分析

以五轴加工中心各项精度指标的初始精度作为精度衰退的初始精度，记录所测得的各项精度指标的精度数据并将数据代入公式(1)(2)，可以计算出各精度指标在各时间节点的精度保持度。以2018年11月05日轴定位的精度保持度为例，通过式(1)计算轴定位精度从2018年10月03日至2018年11月05日共33天的误差变化均值为

然后，代入式(2)计算轴定位精度保持度为

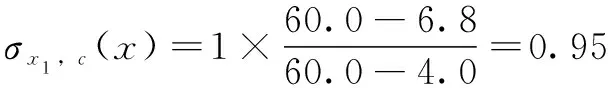
表3所示为各项检测指标精度保持度。在研究过程中认为各个节点的测量指标保持度与时间属于负相关关系，即随着时间的延长精度保持度逐步降低，但始终大于0。在第一次测量中，各个精度指标误差就是最初的出厂值，精度保持度等于1。在最后的测量时间节点时，可以确定最高和最低的精度保持度，其中最高值是0.83，对应着轴旋转精度保持度；而最低值是0.69，对应着轴沿轴直线度。

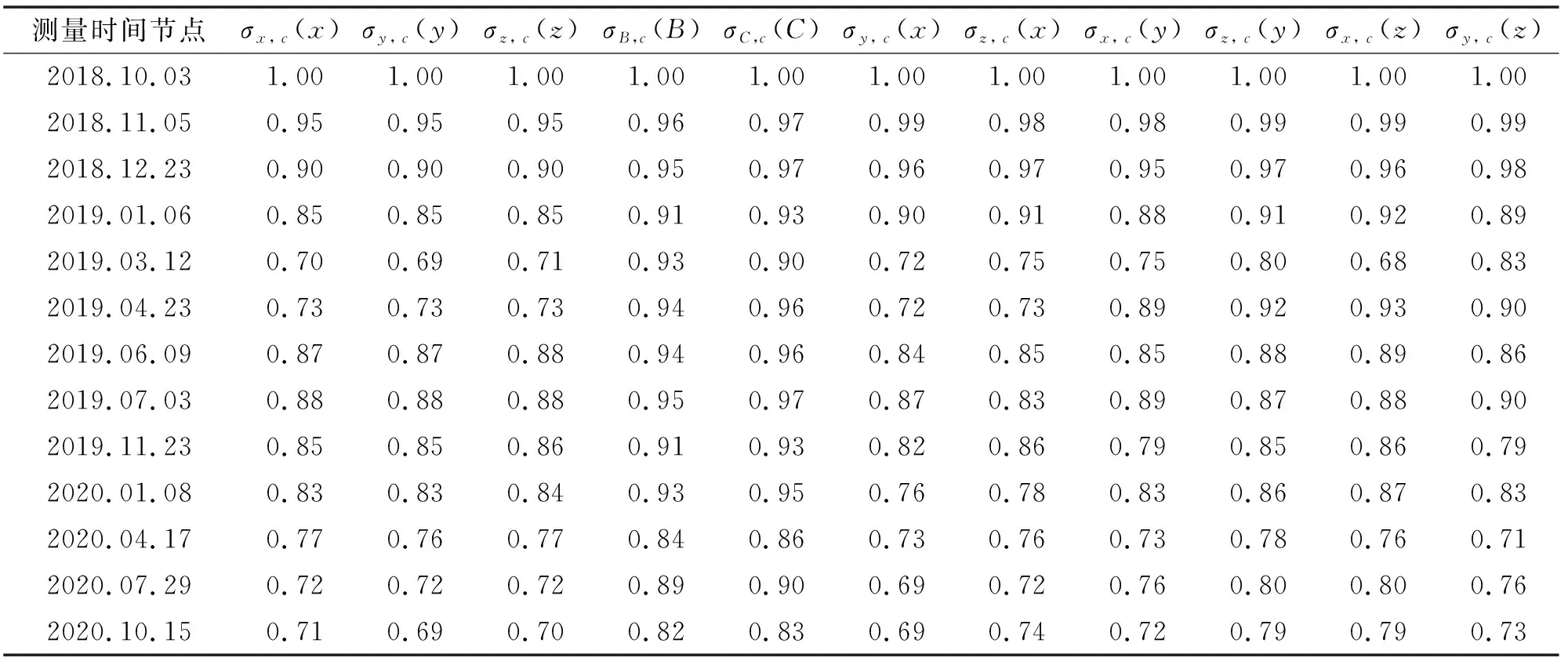
表3 各项检测指标精度保持度

在公式(1)中代入-轴五轴加工中心测量的指标误差，然后对加工中心处于不同时间节点的误差变化均值进行计算，将计算结果代入公式(3)—(9)中。基于这种方式，可以得到在、、轴的空间位置精度保持度如表4所示。可知：在最初时精度保持度降低速度较高；随着时间的发展，中期时精度保持度开始保持稳定，后期会出现一定的降低，然后达到一定程度之后继续保持平稳；到达最后测量时间时，-轴五轴加工中心在轴的空间位置精度保持度最高，为083；-轴五轴加工中心在轴方向的空间位置精度保持度最低，为0.71。

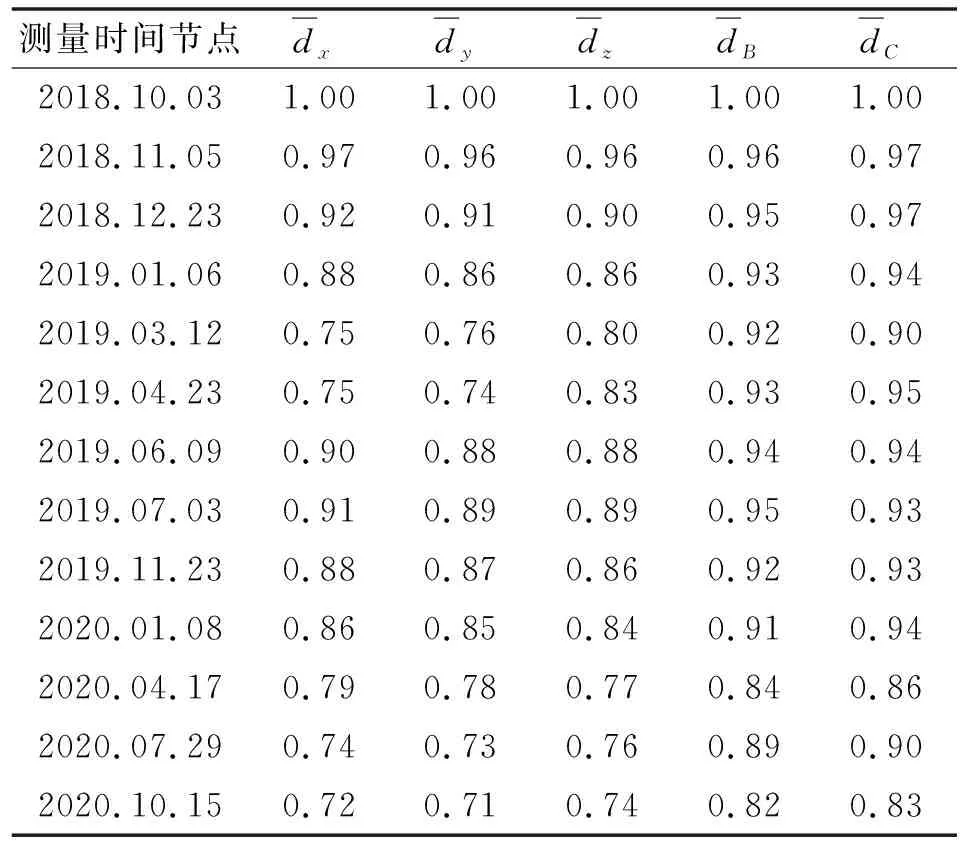
表4 五轴加工中心沿x、y、z轴方向的空间位置精度保持度

4.3 敏感度分析

为分析-轴五轴加工中心敏感度，将743天之内测量的11项精度指标误差在各个测量时间节点的误差为基本参量，构造概率模型；提取最大、最小误差变化均值。在研究过程中认为各个精度指标的误差变化均值始终在最大、最小值间均匀分布。然后，进行任意采样，得到的样本数为2 500。在敏感度分析中利用蒙特·卡罗方法，并对输入、输出量进行了计算研究。其中，前者主要是各误差变化均值，后者主要表示空间位置精度保持度，分别对应着、、轴方向，、轴旋转方向。对应的敏感度分别表示为、、、和。

各误差空间位置精度保持度敏感度如图5所示。可知：对于、、轴空间位置精度保持度的影响因素，按照影响大小依次是此方向的定位精度、其他方向的直线度，而这两个因素的敏感度存在显著的差异性。

图5 各误差空间位置精度保持度敏感度

通过对五轴加工中心的误差进行蒙特·卡罗敏感度分析，得到以下几点：

(1)如果忽略垂直度、旋转轴误差两个因素，则处于直线上的精度保持能力只与两个因素有关，首先是处于对应方向的定位精度；其次是其他方向的精度指标变化特征，而精度保持能力不受其他各轴精度指标的影响。

(2)详细分析各精度指标的精度保持度变化对其空间位置精度保持度的影响。结果表明：与其他各个精度指标相比，精度指标()对五轴加工中心空间位置精度的影响更大。因此，为提高精度保持性，必须合理控制精度指标()的误差，提高五轴加工中心整机精度保持性。结合上述分析可知，各项误差空间位置精度保持度的敏感度受到多种因素的影响，一方面与精度指标误差直接相关；另一方面还会受到加工中心结构特征的影响。