颤振信号下的电液比例多路阀系统稳定性分析
2022-09-20肖乃鑫徐雷余方超叶宗鑫
肖乃鑫,徐雷,余方超,叶宗鑫
(四川大学机械工程学院,四川成都 610065)
0 前言
多路阀是一种集成程度很高的主控阀,因具备结构紧凑、管路连接简单等优点而广泛用于工程机械、航空航天、船舶、陆装等重大装备领域。其性能的好坏直接决定了整机的性能,故研究多路阀系统的稳定性对于保证整机的稳定性具有重要意义。
多路阀因加工误差等原因会导致工作过程中阀体与阀芯之间产生摩擦而影响系统输出,实际应用中常采用颤振信号进行补偿以获取更高的控制精度。有关学者针对摩擦及其补偿进行了研究。薛殿伦和周家豪对先导电磁阀主阀进行热固耦合分析,得到随热变形增加阀芯间隙减小,对污染物尺寸更敏感,摩擦力随污染物尺寸的增大而增大。YANG等为提高数控机床进给系统定位精度,从颤振补偿和非线性摩擦预测控制2个方面讨论了各运动关节处非线性摩擦的有效补偿和控制方法,并证明了所提出方法的正确性。龚国芹等在分析金属软管的漏油问题时发现,过大的颤振信号幅值引起比例方向阀进油口压力强烈波动,最终导致金属软管失效。以上研究表明,摩擦力对机械系统影响较大,对系统采用颤振补偿是十分必要的,而颤振信号会对系统稳定性产生影响。因此,在设计环节对颤振输入系统进行稳定性分析可为确定颤振信号提供理论支撑。在分析中,采用的仿真模型准确度越高,得到的分析结果参考价值越高。对于多路阀,在系统稳定性分析时,将主阀阀芯间隙与偏心考虑在内时得到的结果更准确。
本文作者以某型号电液比例负载敏感多路阀为研究对象,依据Stribeck摩擦模型构建出电液比例系统的AMESim模型,在考虑多路阀主阀阀芯存在直径间隙和偏心的基础上,分析颤振输入的幅值、频率和阀前阻尼孔直径对该系统稳定性的影响。分析结果可为多路阀设计与优化提供参考,使多路阀具备较高的稳定性。
1 电液系统颤振补偿机制
1.1 Stribeck模型
工程中,物体所受摩擦力分为静摩擦力和动摩擦力,前者是位移的函数,后者是速度的函数。在Stribeck摩擦模型中,当系统克服最大静摩擦力开始运动时,随着速度的增加,摩擦力逐渐降低,当速度增大到超过某一临界值时,在黏性动摩擦力的作用下摩擦力又开始上升。因此,得到摩擦力的表达式为
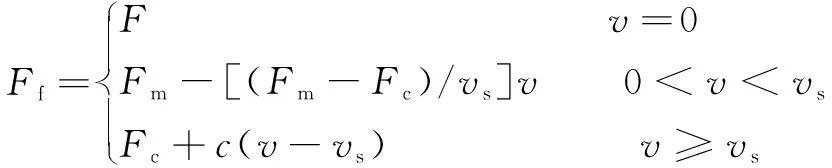
(1)
其中:为静摩擦力;为最大静摩擦力;为库仑摩擦力;=tan。
1.2 电液比例系统数学模型及其颤振补偿
某型电液比例负载敏感多路阀换向阀体结构如图1所示。它具备的电液比例控制特性:以电信号控制电比例减压阀,其输出压力作用于主阀的控制弹簧腔,使主阀阀芯克服摩擦力和弹簧预压力后按比例移动,最终实现进入执行器的流量调节。其基本原理框图如图2所示。
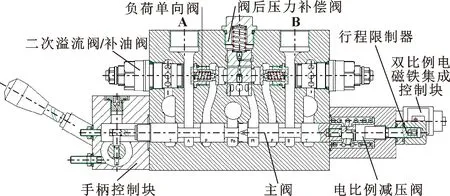
图1 某型号电液比例多路阀换向阀体剖视图

图2 电液比例控制原理框图
在此电液比例系统中,主阀阀芯运动模型为
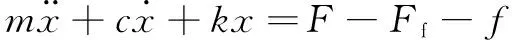
(2)
其中:为主阀控制腔的力;为液动力;为摩擦力。
颤振补偿是一种常用的摩擦补偿方式,即在控制信号中叠加颤振信号,使阀芯在运动过程中始终处于浮动状态,以达到减小摩擦的目的。对此系统进行颤振补偿时,在电比例减压阀的输入信号中叠加颤振信号,得到的控制信号为
=+sin(+)
(3)
在理想状态下,电比例减压阀的输出压力与输入电信号成比例,此时主阀阀芯控制腔的力为
=+sin(+)
(4)
由式(2)(4)求得阀芯速度为0<<时,存在负阻尼效应时的主阀阀芯运动位移为
=e-(sin+cos)+sin(+-
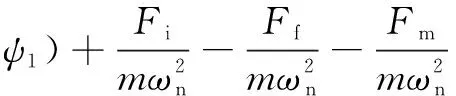
(5)
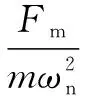
因此,选取具有适当频率和幅值的颤振信号可减小摩擦力,提高系统的控制精度。但信号的频率和幅值不可过大,以免阀芯阀体磨损、系统过大振荡,同时也要避开系统的固有频率。
2 基于AMESim的电液比例系统仿真模型
提取出电液比例多路阀中实现比例控制的电比例减压阀和主阀,利用AMESim的HCD库搭建如图3所示的电液比例系统颤振输入仿真模型。考虑到实际生产中液压阀均存在加工误差以及后期的磨损,为使仿真模型的精确度更高,设置阀芯与阀体间的直径间隙、偏心率和圆角直径分别为0.06、0.5和0.005 mm。其他主要参数如表1所示。
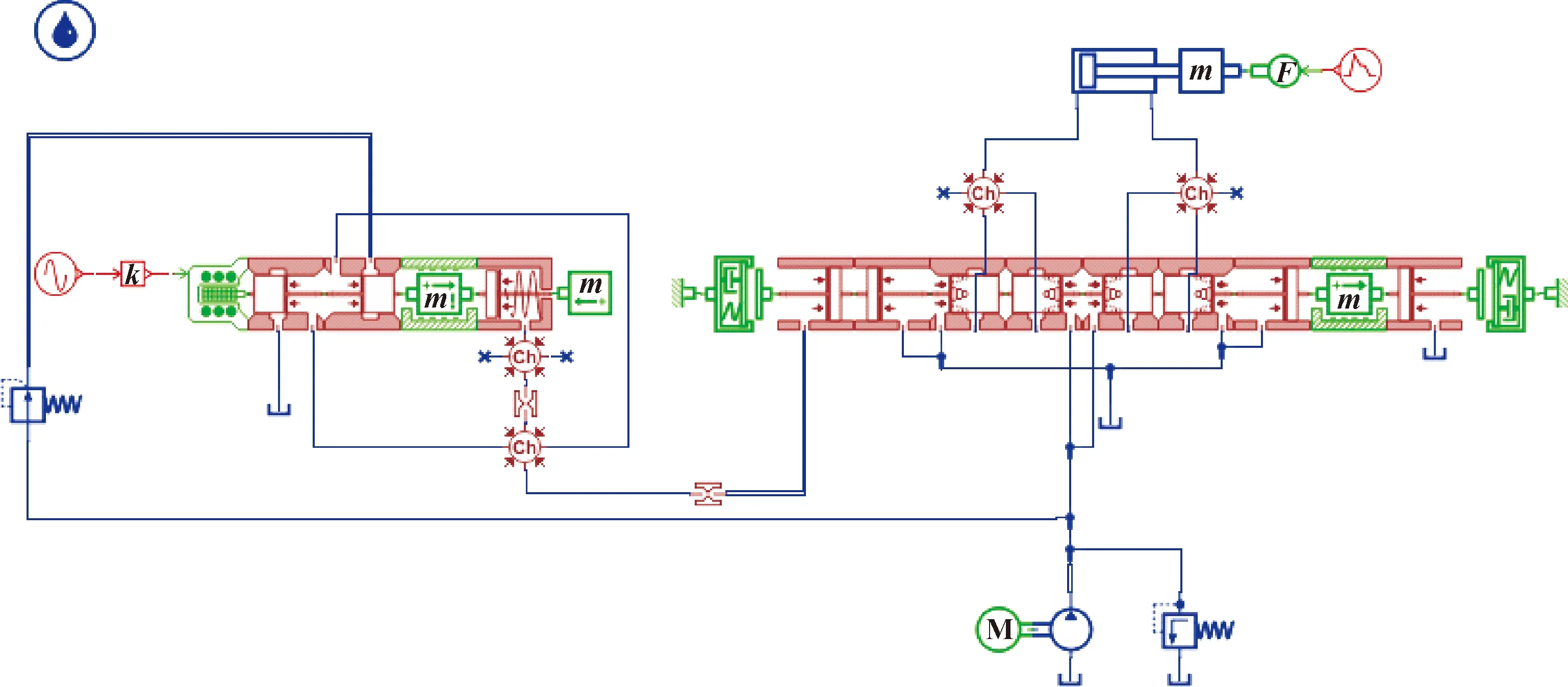
图3 电液比例系统颤振输入仿真模型

表1 主要参数
3 颤振输入信号对系统稳定性的影响
根据叠加颤振信号后的输入信号表达式:=+sin(2π+),设置阶跃输入信号=18 mA、相位=0,叠加的颤振幅值和频率的值利用AMESim的批处理功能进行设置,以得到幅值和频率对系统中主阀阀芯位移以及主阀输出流量的影响。
3.1 颤振信号频率的影响
设置颤振幅值=2 mA,仿真得到频率为40~160 Hz时主阀阀芯位移以及输出流量的稳态波动情况,并将不同频率下的稳态波动幅值绘制在折线图中,如图4所示。
由图4可知:主阀芯位移和输出流量的波动频率等于输入信号的频率;当输入信号频率由40 Hz增大到160 Hz时,主阀阀芯位移的波动幅值由0.204 mm逐渐减小到0.014 mm,主阀输出流量的波动幅值由2.064 L/min逐渐减小到0.134 L/min,两者的波动幅值变化趋势保持一致。
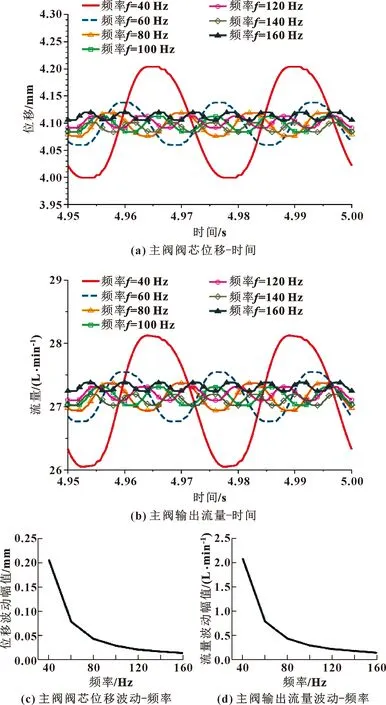
图4 不同频率下系统各参数的稳态波动情况
随着输入信号的频率逐渐增大,主阀波动幅度逐渐减小,同时幅值减小趋势也逐渐减慢。因此,在确定颤振信号时,选择偏大的频率可使系统稳定性提高,但过大的频率对波动幅值的降低效果不明显,还会引起系统振荡。
3.2 颤振信号幅值的影响
设置颤振频率=100 Hz,仿真得到颤振幅值为1.5~5 mA时主阀阀芯位移以及输出流量的稳态波动情况,如图5所示。

图5 不同幅值下系统各参数的稳态波动情况
由图5可知:当幅值达到2 mA时,阀芯才克服摩擦力引起的爬行现象,开始处于颤振运动状态;当颤振输入信号的幅值由2 mA增大到5 mA时,主阀阀芯位移和输出流量的波动频率均为100 Hz,等于输入信号的频率,主阀阀芯位移的波动幅值由0.028 mm逐渐增大到0.147 mm,主阀输出流量的波动幅值由0.294 L/min逐渐增大到1.519 L/min,两者的变化趋势仍保持一致。
可见,在颤振状态下,随着颤振输入信号幅度的增加,主阀的波动幅值增加,其波动频率等于输入颤振信号的频率。在选择颤振信号的频率时,过小的颤振幅值不能克服摩擦力的影响,而过大的颤振幅值会使系统产生振荡。在合适的范围内,偏小的颤振信号能够保证系统具备较好的稳定性,一般情况下其值为阶跃输入信号的10%~25%,对于此系统为1.8~4.5 mA。
4 系统内部结构的影响分析
电比例减压阀与主阀间设有的阻尼孔与主阀控制阀之间形成了半桥结构,减小了超调量,增强了系统稳定性。为探究阻尼孔直径对颤振输入系统稳定性的影响,设置阻尼孔直径分别为1、1.5、2、2.5、3 mm,仿真得到阻尼孔直径对主阀阀芯位移和输出流量参数的影响,如图6、图7所示。
由图6可知:阻尼孔大小直接影响系统的响应时间,阻尼孔越大响应时间越短,但当阻尼孔直径超过2.5 mm时,系统出现超调,且随着阻尼孔直径的增大,超调量增大。由图7可知:阻尼孔大小也会影响系统各量的波动,当阻尼孔直径由1 mm增加到3 mm时,主阀阀芯位移由0.054 mm增大到0.079 mm,输出流量的波动幅值由0.53 L/min增大到0.76 L/min,且两者的增长趋势逐渐减慢。
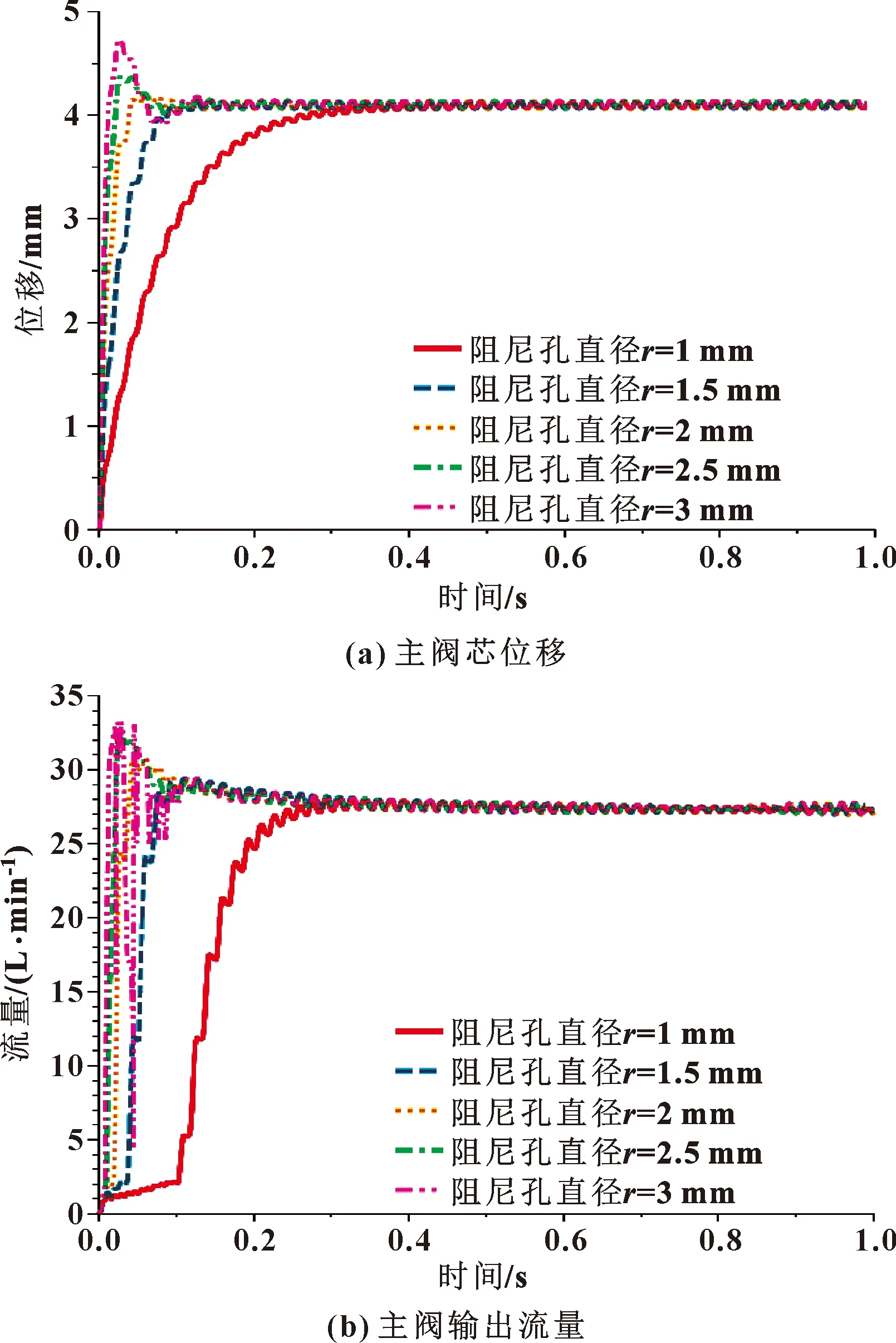
图6 响应时的参数变化
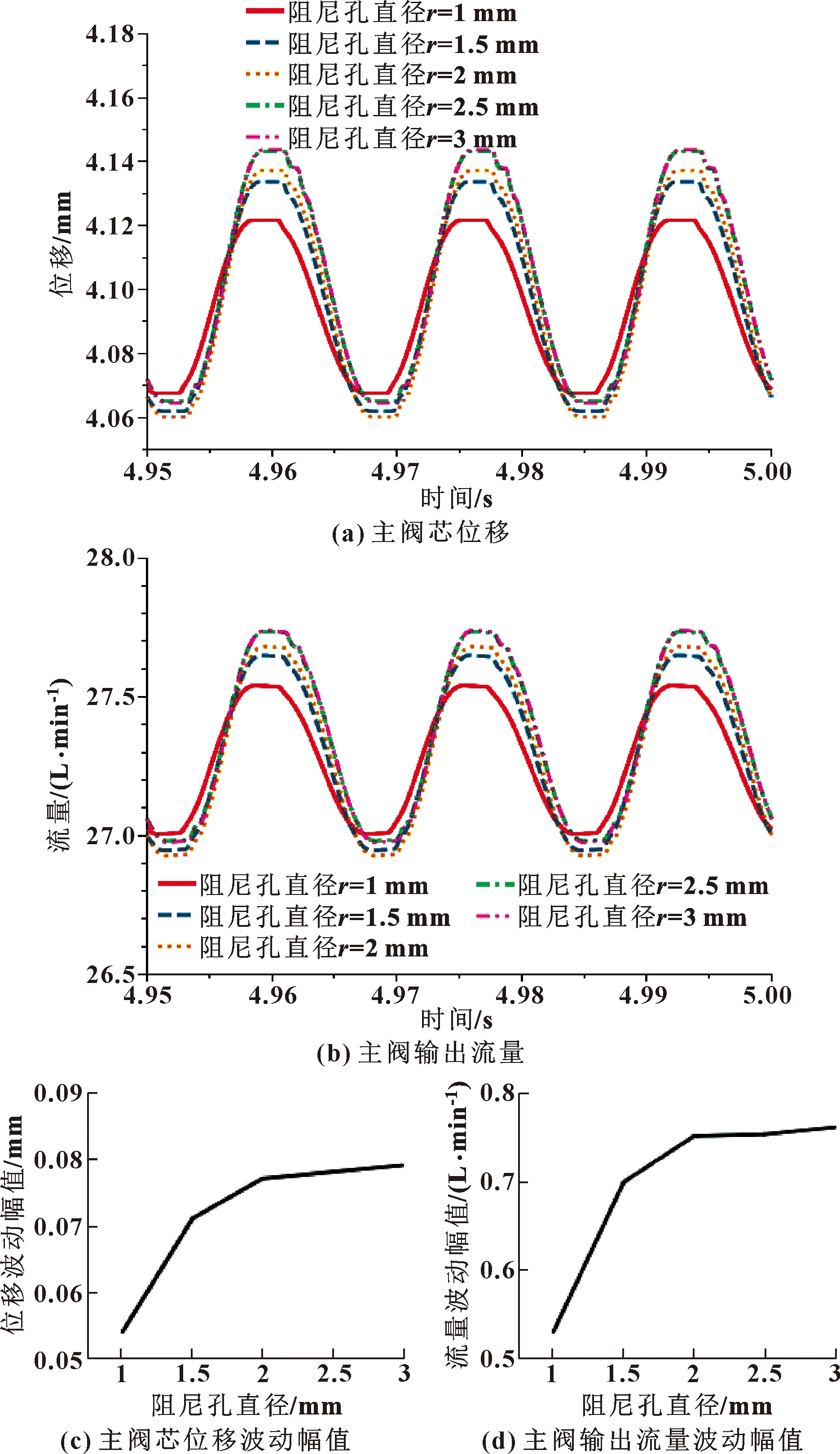
图7 不同阻尼孔直径下稳态时系统参数变化
可见,小直径的阻尼孔可以使系统具备更高的稳定性,降低甚至消除超调量,但是会使响应时间增长。而较大的阻尼孔可降低系统的响应时间,但会使系统参数的波动增大、超调量增大、稳定性降低。具备不同阻尼孔直径的系统需要选择合适的颤振输入信号,使系统稳定性满足要求的同时,能够减小超调量和提高响应速度。
5 结论
本文作者对颤振输入电液比例多路阀系统进行稳定性分析时,在考虑主阀阀芯出现间隙和偏心情况的基础上,分析了外部输入信号的颤振幅值和频率以及内部主阀前阻尼孔直径对多路阀系统稳定性的影响,得到以下结论:
(1)针对外部输入信号:系统的波动幅值随颤振信号幅值的增大而增大。随着颤振频率的逐渐增加,系统的波动幅值逐渐减小,稳定性逐渐升高。因此,选择合适的范围内具有偏小幅值和偏大频率的颤振信号可使系统具备良好的稳定性。
(2)针对系统内部的主阀前阻尼孔直径:主阀前阻尼孔直径减小,系统参数的波动幅值减小,超调量减小,但系统响应变慢。因此,具备不同阻尼孔直径的系统在选择合适的颤振输入信号时要同时考虑系统稳定性、超调量和响应速度。
(3)采用AMESim软件对多路阀进行建模,可以有效模拟出电液比例多路阀的工作原理及工作状态,为多路阀在设计环节中选取合适的颤振输入信号提供参考,有助于提高多路阀的使用性能。
