圆弧连接几何作图法研究

1 引言

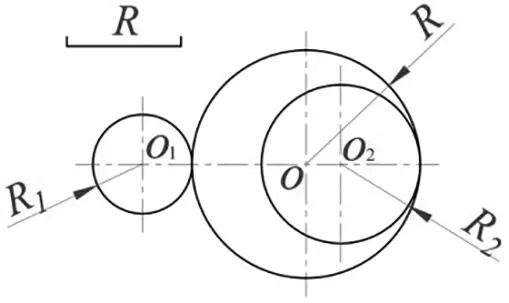
1.1用已知半径的圆弧相切连接已知圆心位置和半径的两圆(或两圆弧)，有三种连接形式：外连接、内连接、内外连接，连接形式如图1所示，AB段圆弧为已知半径的圆弧，O

和O

为已知圆心位置和半径的两圆。

在《机械制图》教材中，对于上述圆弧连接的几何作图方法为：

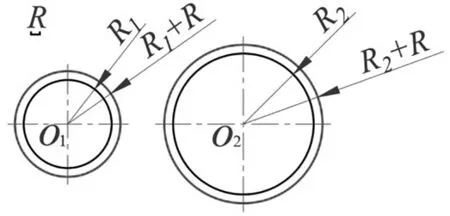
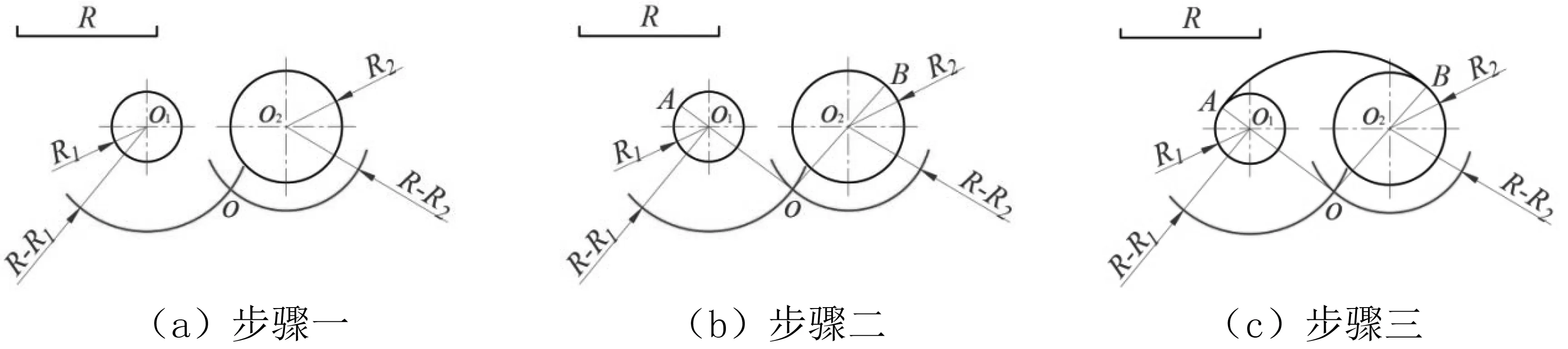
(1)外连接圆弧：分别以O

、O

为圆心，以R+R

、R+R

为半径画弧，相交于O点(连接弧的圆心)，连接OO

、OO

，分别交两圆于A、B两点(为切点)，再以O点为圆心，以R为半径，在A、B之间画圆弧。

(2)内连接圆弧：分别以O

、O

为圆心，以R-R

、R-R

为半径画弧，相交于O点(连接弧的圆心)，连接OO

、OO

并延长，分别交两圆于A、B两点(为切点)，再以O点为圆心，以R为半径，在A、B之间画圆弧。

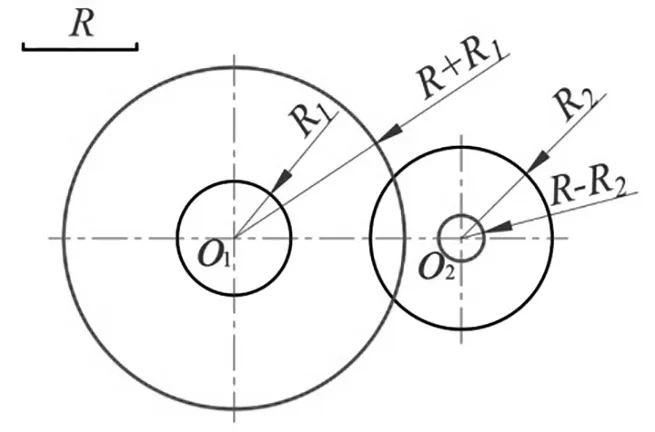
(3)内外连接圆弧：分别以O

、O

为圆心，以R+R

、R-R

为半径画弧，相交于O点(连接弧的圆心)，连接OO

,交圆弧与A点，连接OO

并延长，交圆弧与A点(A、B为切点)，再以O点为圆心，以R为半径，在A、B之间画圆弧。该作图方法所求圆弧与圆O

外接，与圆O

内接。

经过上述案例分析得知，在有些情况下，无法按照教材中的作图方法完成圆弧连接，存在上述现象的原因是R

、R

、R、O

O

和L的取值没有受到限定。

Keras是用Python开发的开源深度学习库，能够以Tensor⁃Flow、Theano或CNTK作为后端引擎。TensorFlow最初是由Google开发的开源深度学习库，功能强大，执行效率高，并提供了Python、C++等多种语言编程接口。通过TensorFlow，Keras可以在CPU、GPU上无缝运行[2]。Keras简单易用，利用Keras可以快速开发深度学习模型，支持卷积网络和循环网络以及两者的组合，并能够构建任意深度的学习模型。

在《机械制图》教材中，对于上述圆弧连接的几何作图方法为：

妈妈说：“把卷子拿来。”我看得出妈妈是压着气，不一会儿，彗星就要撞地球了。出乎意料地，她竟然没有打我。小兔子都到手了，狼还不下口。

利用重复控制跟踪的统一潮流控制器抑制系统强迫振荡方法//蒋平,陈琼,吴熙,蔡晖,祁万春,谢珍建//(18):64

(2)内连接圆弧：以O

为圆心，以R-R

为半径画弧，作与EF线相距为R的平行线，相交于O点(连接弧的圆心)，连接OO

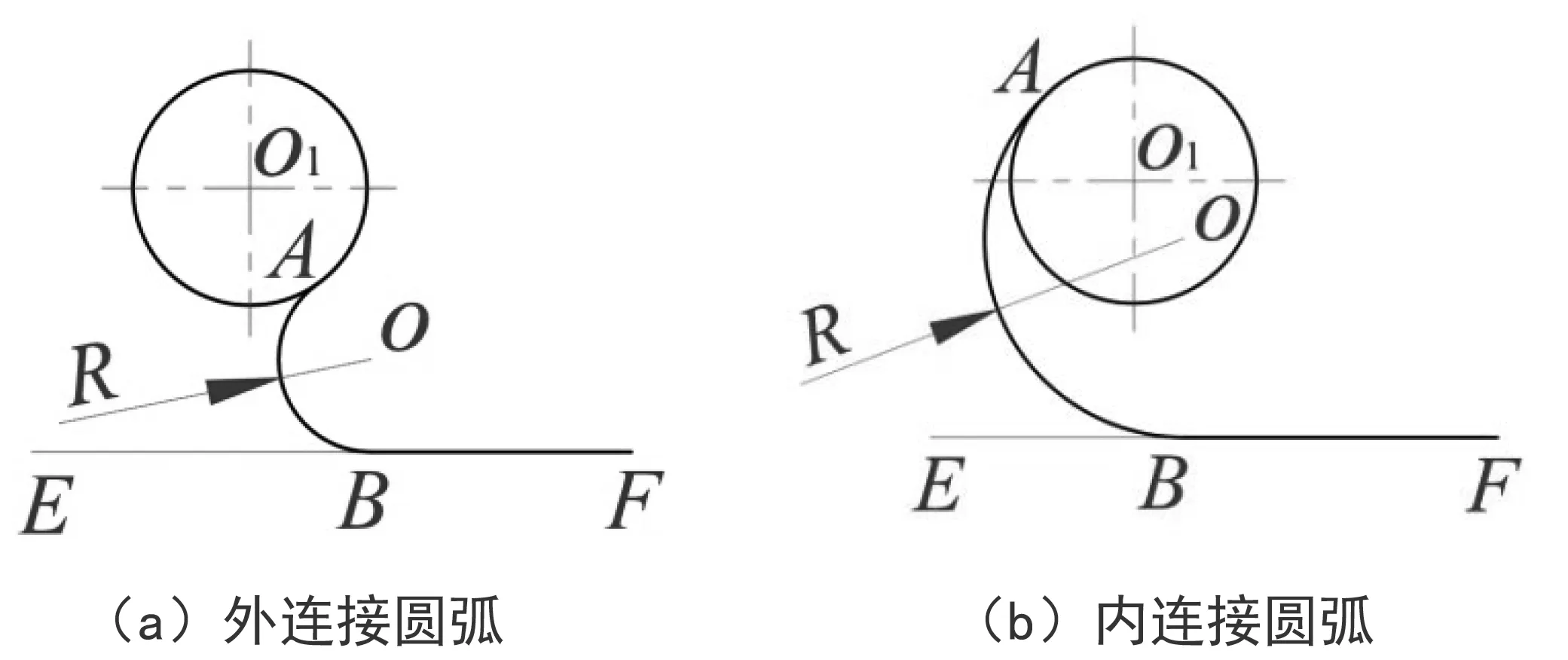
，交圆于A点(为切点)，同时从O点向EF线作垂线，垂足为B点(为切点)。再以O点为圆心，以R为半径，在A、B之间画圆弧。

水下混凝土配合比需要结合理论计算以及相关实验来进行验证，当前混凝土实验强度要高于设计强度，实际坍落度需要控制在18～20cm之间，水灰比控制在0.5～0.6m，粗骨料可以选用砾石。目前水下混凝土输送方式较多，比如混凝土输送泵进行灌注，此类技术措施在目前高速公路以及桥梁工程中应用范围较广。导管实际分节长度需要进行控制，这样便于后续拆卸与运输，对焊缝质量进行控制。导管在吊装之前需要进行试拼，确保接口位置连接具有良好的牢固性。

2 问题分析

在用上述方法进行绘图时，如果遇到某些特殊情况，将无法完成圆弧连接。现分别对两种圆弧连接中存在的问题进行举例分析。

2.1 两圆间圆弧连接

(1)外连接圆弧

设R

=5，R

=8，R=1，O

O

=20，按照该已知条件绘图，得到的结果如图3所示，图中半径为R+R

、R+R

的两圆没有交点，因此无法按照教材中所述的方法完成圆弧连接。

(2)内连接圆弧

1)设R

=5，R

=8，R=1，O

O

=20，则R-R

、R-R

均小于0，无法作图。

2)设R

=5，R

=8，R=12，O

O

=20，则得到的图形如图4所示，图中半径为R-R

、R-R

的两圆弧没有交点，因此无法按照教材中所述的方法完成圆弧连接。

(3)内外连接圆弧

1)设 R

=5，R

=8，R=1，O

O

=20，则R-R

小于0，无法作图。

2)设R

=5，R

=8，R=10，O

O

=20，则得到的图形如图5所示，图中半径为R+R

、R-R

的两圆弧没有交点，因此无法按照教材中所述的方法完成圆弧连接。

2.2 圆和直线间圆弧连接

(1)外连接圆弧

(1)无论溶洞存在与否，管片在自重应力作用下的应力分布以及管片在列车动载作用下的应力增量分布都无明显变化。但溶洞存在时，管片的应力响应会有所增加。

(1)外连接圆弧

(2)内连接圆弧

941 Prevention and treatment of stroke in China: the status and future

2)设R

=5， R=7，O

与EF线距离L=10，则得到的图形如图7所示，图中半径为R-R

的圆与距离EF为R的平行线GH线没有交点，因此无法按照教材中所述的方法完成圆弧连接。

基于市政道路桥梁过渡段的路基路面施工技术研究……………………………………………………… 杨艳丽（3-84）

或许你并不清楚，我们常喝的加多宝、王老吉、六个核桃等饮料的纸袋，其实都是使用正博的机器所生产。事实上，正博制袋机的销售就是这样火爆，市场销售额在2017年“爆炸式”增长了36%。

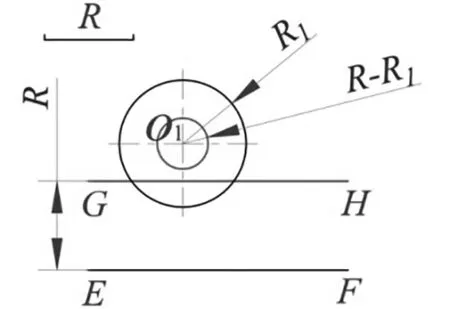
1.2用已知半径的圆弧相切连接已知圆心位置和半径的一个圆(或圆弧)与已知位置的直线，有两种连接形式：外连接、内连接，连接形式如图2所示，AB段圆弧为已知半径的圆弧，O

为已知圆心位置和半径的圆,EF为已知位置的直线。

3 圆弧连接的几何作图法研究

3.1 两圆间圆弧连接

设R

=5， R=2，O

与EF线距离L=10，按照该已知条件绘图，得到的结果如图6所示，图中半径为R+R

的圆与距离EF为R的平行线GH线没有交点，因此无法按照教材中所述的方法完成圆弧连接。

假设R

、R

和O

O

的取值不变，只增加R的值，当R的值增大到一定程度的时候，将存在如图8所示的特殊情形，图中R=(O

O

-R

-R

)/2。

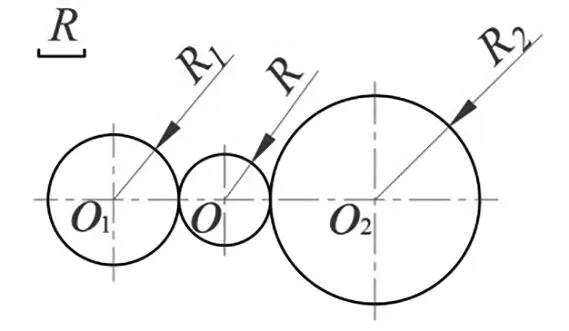
图8所示的特殊情形可看作是圆O将圆O

和圆O

用外切的方式连接了起来，具体的作图方法与教材中描述的并不一致。

锂电池隔膜生产线工艺运行对环境温度要求较严，大部分工段全年要求恒温恒湿且工艺设备表面不得结露，否则会直接影响产品的质量。因此，保证空调系统冷冻水的温度也是保证工艺生产出合格产品的重要条件。鉴于工艺冷冻水室外部分量小且要求不高，在设计中将工艺与空调冷冻2个系统合二为一，冷冻水供水温度按工艺厂房空调用水要求设计，管线设置按工艺设备冷冻用水要求设计。这样既保证了厂房空调温度要求,也满足了工艺设备冷冻水连续性的要求。同时工艺和空调冷冻机组互为备用，减少了机器的备用台数，降低了工程投资，简化了运行操作。

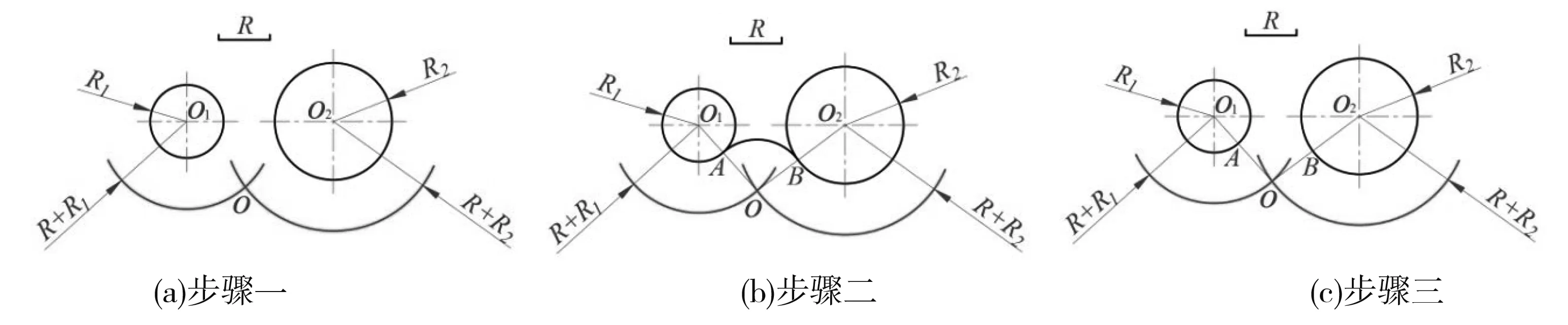
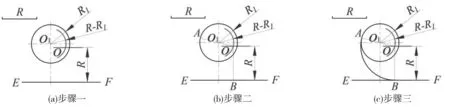
将图8中的R值继续增大，使得R>(O

O

-R

-R

)/2，然后按照《机械制图》教材中“两圆间外连接圆弧”的作图方法作图，即可得到如图9所示的结果，图9(a)是以O

、O

为圆心，以R+R

、R+R

为半径画弧，相交于O点(连接弧的圆心)；图9(b)是连接OO

、OO

，分别交两圆于A、B两点(为切点)；图9(c)是以O点为圆心，以R为半径，在A、B之间画圆弧，AB弧即为所求的外连接圆弧。

可以看出，输入序列(可说明是任何一个序列)与单位抽样序列的卷积就是序列本身。而“输入序列表示成单位抽样序列的移位相加”这个概念，是课程前面已讲解过的知识点，且这个知识的物理意义十分明确，学生理解起来没有什么难度。接下来，再将输入序列与单位脉冲响应序列卷积的公式写出，对比讲解。

(2)内连接圆弧

假设R

、R

和O

O

的取值不变，只增加R的值，当R的值增大到一定程度的时候，将存在如图10所示的特殊情形，图中R=(O

O

+R

+R

)/2。

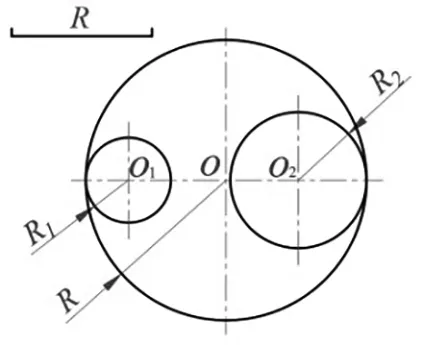
图10所示的特殊情形可看作是圆O将圆O

和圆O

用内切的方式连接了起来，具体的作图方法与教材中描述的并不一致。

从该试验中水温变化曲线分析认为，造成这种突降变化的干扰因素是在180～200 m的深度区间，并不是来自深部，排除地震前兆异常的可能性。

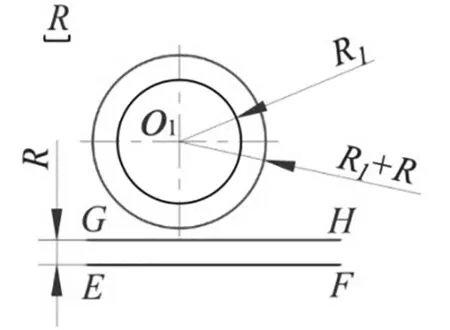
(1)外连接圆弧：以O

为圆心，以R+R

为半径画弧，同时作与EF线相距为R的平行线，相交于O点(连接弧的圆心)，连接OO

，交圆于A点(为切点)，同时从O点向EF线作垂线，垂足为B点(为切点)。再以O点为圆心，以R为半径，在A、B之间画圆弧。

将图10中的R值继续增大，使得R>(O

O

+R

+R

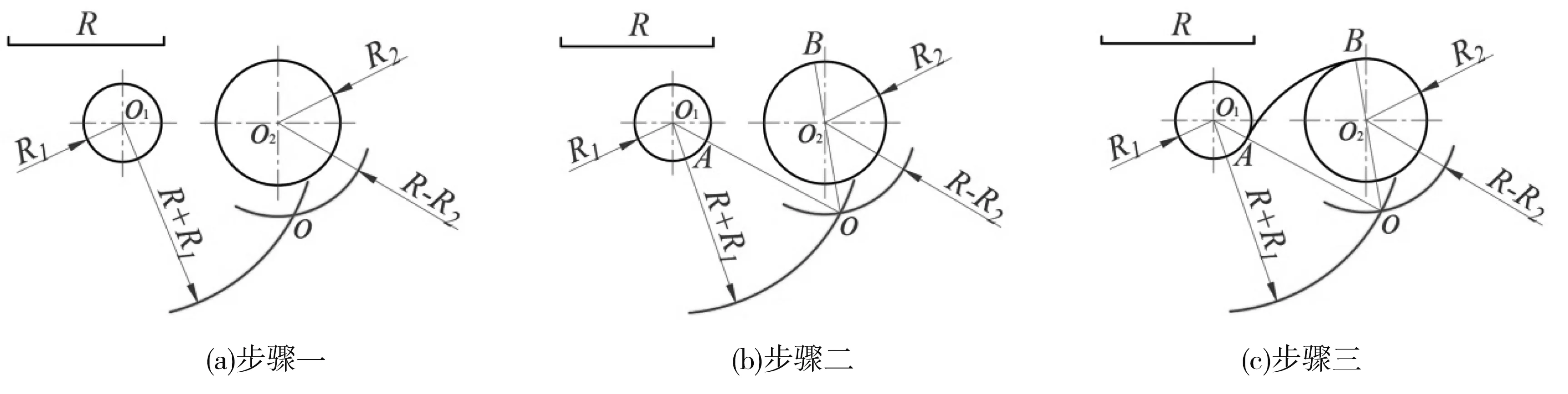
)/2，然后按照《机械制图》教材中“两圆间内连接圆弧”的作图方法作图，即可得到如图11所示的结果，图11(a)是以O

、O

为圆心，以R-R

、R-R

为半径画弧，相交于O点(连接弧的圆心)；图11(b)是连接OO

、OO

并延长，分别交两圆于A、B两点(为切点)；图11(c)是以O点为圆心，以R为半径，在A、B之间画圆弧，AB弧即为所求的内连接圆弧。

(1)外连接圆弧

3)0.6mm渗层刀片不论是在渗层厚度、组织硬度，还是在组织硬度梯度等方面，都介于其他两种渗层刀片之间。虽然在部分位置上出现一定程度的崩刃现象，但磨损量比0.3mm渗层刀片要小，大部分情况下与0.9mm渗层刀片的磨损量相差不大，甚至磨损量比0.9mm渗层刀片要小，崩刃现象也比0.9mm渗层刀片出现的少。因此，0.6mm渗层刀片在磨损量上总体效果最好。

假设R

、R

和O

O

的取值不变，只增加R的值，当R的值增大到一定程度的时候，将存在如图12所示的特殊情形，图中R=(O

O

-R

+R

)/2。

将图12中的R值增大，使得R>(O

O

-R

+R

)/2，然后按照《机械制图》教材中“两圆间内外连接圆弧”的作图方法作图，即可得到如图13所示的结果，图13(a)是以O

、O

为圆心，以R+R

、R-R

为半径画弧，相交于O点(连接弧的圆心)；图13(b)是连接OO

,交圆弧于A点，连接OO

并延长，交圆弧于B点(A、B为切点)；图13(c)是以O点为圆心，以R为半径，在A、B之间画圆弧，AB弧即为所求的内连接圆弧。

在该作图方法中，所求圆弧与圆O

是外连接，与圆O

是内连接，如果要让所求圆弧与圆O

是内连接，与圆O

是外连接，则可将条件变为：R>(O

O

+R

-R

)/2，以O

、O

为圆心，以R-R

、R+R

为半径画弧求得连接弧的圆心O点

。

3.2 圆与直线间圆弧连接

(3)内外连接圆弧

假设R

、直线位置和L的取值不变，只增加R的值，当R的值增大到一定程度的时候，将存在如图14所示的特殊情形，图中R=(L-R

)/2。

图14所示的特殊情形可看作是圆O以与圆O

外切并与直线EF相切的方式连接了起来，具体的作图方法与教材中描述的并不一致。

1)设R

=5， R=1，O

与EF线距离L=10，则R-R

小于0，无法作图。

将图14中的R值继续增大，使得R>(L-R

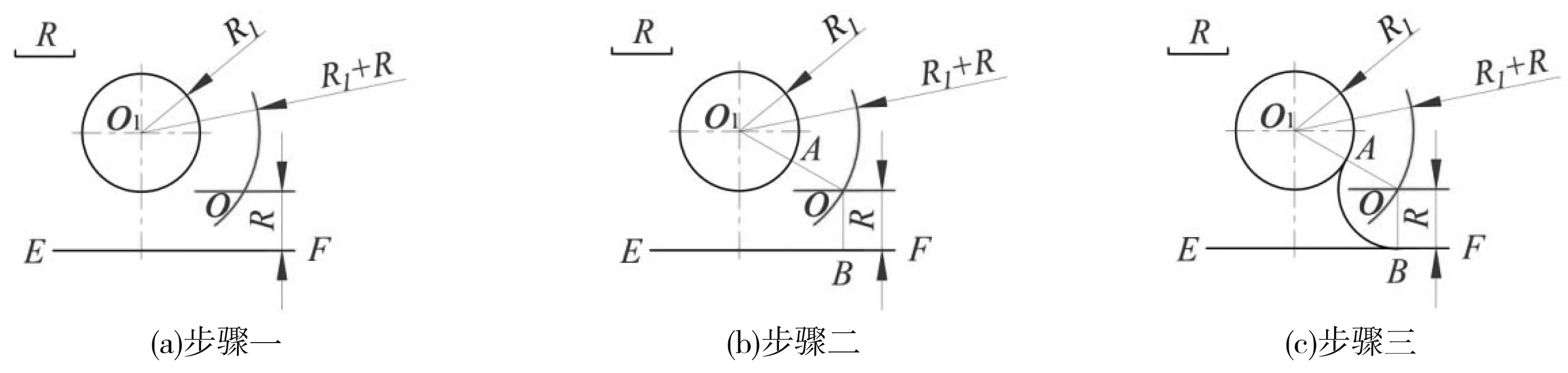
)/2，然后按照《机械制图》教材中“圆与直线间外连接圆弧”的作图方法作图，即可得到如图15所示的结果，图15(a)是以O

为圆心，以R+R

为半径画弧，画与EF线距离为R 的平行线，相交于O点(连接弧的圆心)；图15(b)是连接OO

，交圆于A点(为切点)，过O点作EF的垂线，垂足为B点(为切点)；图15(c)是以O点为圆心，以R为半径，在A、B之间画圆弧，AB弧即为所求的外连接圆弧。

(2)内连接圆弧

根据自由旋转链的均方末端距公式(2),代入基本变量关系L=nl及式(9)和(11),当cos θ趋近于1时,可得

假设R

、直线位置和L的取值不变，只增加R的值，当R的值增大到一定程度的时候，将存在如图16所示的特殊情形，图中R=(L+R

)/2。

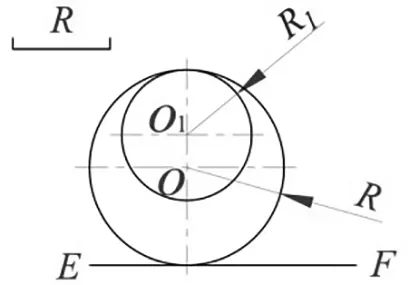
图16所示的特殊情形可看作是圆O以与圆O

内切并与直线EF相切的方式连接了起来，具体的作图方法与教材中描述的并不一致。

将图16中的R值继续增大，使得R>(L+R

)/2，然后按照《机械制图》教材中“圆与直线间内连接圆弧”的作图方法作图，即可得到如图17所示的结果，图17(a)是以O

为圆心，以R-R

为半径画弧，画与EF线距离为R 的平行线，相交于O点(连接弧的圆心)；图17(b)是连接OO

并延长，交圆于A点(为切点)，过O点作EF的垂线，垂足为B点(为切点)；图17(c)是以O点为圆心，以R为半径，在A、B之间画圆弧，AB弧即为所求的内连接圆弧。

4 结论

根据研究可知，要在任意情况下完成圆弧连接的绘制，需对R

、R

、R和O

O

之间的关系，R

、R和L之间的关系进行限定。

(1)两圆间连接圆弧时的条件：

1)外连接圆弧时的条件：R>0，且R≥(O

O

-R

-R

)/2；

2)内连接圆弧时的条件：R>R

，且R≥(O

O

+R

+R

)/2，R

为两半径中较大者；

3)内外连接圆弧时的条件：R>R

，且R≥(O

O

-R

+R

)/2，R

为两半径中较大者，此时所求圆弧与R

外接，与R

内接。

(2)圆和直线间连接圆弧的条件：

1)外连接圆弧时的条件：R>0，且R≥(L-R

)/2；

2)内连接圆弧时的条件：R>R

，且R≥(L+R

)/2。

[1]唐卫东.机械制图[M].北京:高等教育出版社,2017,9-3.

[2]李宗义.机械制图[M].兰州:兰州大学出版社,2016,9-2.

[3]刘哲.高玉芬.机械制图[M].大连:大连理工大学出版社,2011,6-17.

[4]冯秋官.机械制图[M].北京:高等教育出版社,2000,7-1.

[5]王泽荫.机械制图[M].北京:机械工业出版社,2021,14-20.