深度学习视角下的数学概念课教学设计研究

汤 鸿

(江苏省张家港市塘桥高级中学,215600)

深度学习的数学课堂需要理解数学、理解学生、理解教学．理解数学,就是要高屋建瓴地把握数学内容的本质,站在系统的高度认识数学,特别是对数学内容所蕴含的数学思想和方法要有深入理解;理解学生,就是要全面了解学生的思维规律,把握学生的认知特点;理解教学,就是要把握教学的基本规律,按教学规律办事[1]．数学教学要做到“不在知其然,而在知其所以然;不在知其所以然,而在何由以知其所以然”．由此才能实现“启发学者,示以思维之道”的教学．

在概念课的教学设计中，需要深入思考隐藏在客观事物背后的是什么数学知识、数学规律?这个数学知识的本质属性是什么?统摄具体数学知识与技能的数学思想方法是什么?某个具体内容的数学本质既表现为隐藏在客观事物背后的数学知识、数学规律,又表现为隐藏在数学知识背后的本质属性,还表现为统摄具体数学知识与技能的数学思想方法.由此深度学习的数学概念课堂尤其重要[2]．本文对此进行探究.

一、重视概念的形成和发展,对概念本质及思想深度学习

数学概念作为数学最为关键的构成内容之一,需要予以充分的关注．在开展数学概念教学的过程中,要让学生充分体会到数学概念的形成以及发展过程,进而让学生能够更加深入了解数学概念的本质以及其中的思想,主动对自身的知识体系进行优化,这也是数学概念深度学习的机遇点．在进行授课前,需要做好充足的准备工作．

对“数系的扩充”这节内容,可以和学生一起沿着历史的足迹,重温数的发展历程即数系不断扩充的过程,了解数系发展的两个重要方面:一是数系的扩充是生产实践与社会发展的需要;二是数系的扩充是数学内部发展的需求(如解决运算中的矛盾等).

(1)负数是如何产生的?《九章算术》是世界上最早详细记载负数和运算法则的著作．

(2)分数是如何产生的?《九章算术》第二章“粟米”，粮食的按比例折换;第三章“衰分”，比例分配问题;第六章“均输”，合理摊派赋税等，对此都有明确记载．

无论是负数、分数的确切定义和科学表示,还是分数的算法,最早建立起来的都是中国,比欧洲早1 400年．

(3)无理数是如何产生的?公元前500年,毕达哥拉斯学派提出“万物皆数”;门徒希伯索斯发现一个惊人的“悖论”:两直角边长均为1的直角三角形的斜边长不是整数或分数!

瑞士数学家欧拉取imaginary(想像的、假想的)一词的词头i表示平方等于-1的“新数”.“新数”i,叫做虚数单位．

在备课时要注意将数学概念的形成以及发展过程融入教学,让学生能够在学习的过程中更好地理解数学概念.同时还需要引导学生主动进行数学概念的探究和理解,进而让学生能够充分发挥自身的思维能力,最终让学生的深层次思维水平得到有效提升．

二、巧妙利用现有知识,引导学生进行概念的深度学习

要注意在新旧知识体系之间建立起合理的联系,让学生在温习已学知识的同时,更好地了解新的知识．特别是在进行一些抽象概念的学习时,需要引导学生借助旧的知识进行思考,进而有效增强学生学习新知识的能力．

在必修内容“立体几何初步”中,学生已经学习了如何求两条异面直线所成的角,所用的方法是通过平移把两条异面直线所成的角转化为两条相交直线所成的角,这是研究的基本思路,但这种转化往往需要一定的技巧,具体计算也比较烦杂．从本质上讲,角度是组成角的两条射线的“方向差”,因此只要知道两条直线的方向向量,就能利用向量工具求出两条异面直线所成角的度数,而不需要进行平移,再构造三角形进行计算．利用向量方法求两条异面直线所成的角、直线与平面所成的角以及平面和平面所成的夹角,都可以不作出角.研究两条直线之间的角只需研究两条直线的方向向量的夹角；研究直线与平面所成角只需研究直线方向向量和平面法向量的夹角;研究两个平面所成角只需研究两平面法向量的夹角．解题步骤如图1所示.

这种类比旧知、引入新知的教学方法,不仅能够大幅提升教学的效率,还能够很好地让学生体会学习新知的重要性．概念课的引入可以充分利用知识间的内在联系,针对学生的知识储备或易混淆的概念,采用数学知识内部的联系创设问题情境,引导学生进行对比、总结,得出相关结论．这样不仅能激发学生探究问题的动机,也有助于学生形成知识结构．在数学概念课中,问题情境起着至关重要的作用,通过情境引出需要探究的问题,激发学生对问题进行探究的欲望．

三、借助问题式教学,帮助学生构建深度数学概念

深度学习的核心内容是学生自身的学习以及体验,需要引导学生积极进行新知识的学习以及探索．可以结合实际的教学内容,设计一系列由浅入深、层层递进的问题,引导学生主动对所学内容进行进一步的思考和理解,并借助这些知识去解决一些实际问题,让学生充分了解数学概念的整个形成和发展周期,进而让学生能够在使用知识、学习知识的过程中进行知识的深度构建．

在“函数零点”概念课教学时,先提出:

问题1(1)方程x2-x-6=0有根吗?

(2)方程x6+x-3=0有根吗?

问题2作出函数f(x)=x2-x-6的图象,观察函数图象与方程x2-x-6=0的根有没有联系?

设计意图先从“数”的角度研究方程x2-x-6=0的根,再引出本节课的新课内容,把使函数f(x)=x2-x-6的值为0的实数x称为函数f(x)=x2-x-6的零点．问题2从形的角度,由函数f(x)=x2-x-6的图象与x轴交点横坐标,进一步理解零点定义．

问题3判断函数f(x)=x2-2x-1在区间(2,3)上是否存在零点?

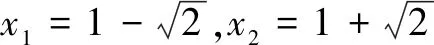
再作出函数f(x)=x2-2x-1的图象,因为f(2)=-1<0,f(3)=2>0,发现二次函数f(x)=x2-2x-1图象在区间[2,3]上是不间断的,这表明此函数图象在区间(2,3)内一定与x轴相交,即函数在区间(2,3)上存在零点.

问题4若函数y=f(x)为二次函数,则它满足下列哪个条件时,函数y=f(x)在(a,b)上有零点?

(1)f(a)<0,f(b)>0；

(2)f(a)>0,f(b)<0；

(3)f(a)>0,f(b)>0；

(4)f(a)<0,f(b)<0.

问题5函数y=f(x)满足什么条件时,函数在区间(a,b)上有零点?

在经历上面5个问题后,学生能通过自己的语言将零点存在定理描述出来,完成本节课的教学难点．

在数学概念教学时,设计的问题需要具有启发性,能够帮助学生通过思考去提高自身的思维深度以及广度；需要符合学生的“最近发展区”,具有层次性、递进性,能激发思维,有效实现课程目标的达成．设计好的数学问题,需要让学生感到问题有难度,但是经过努力能够达到,解答后能体会一种“成功”的喜悦,渴望继续解决一个问题．通过这样的问题, 能够突破教学的重点、难点,培养学生分析问题、解决问题的能力．

四、设计情境创设中的变式,促进数学概念深度学习

创设情境进行教学本身就可以提升学习兴趣,帮助学生更好地理解数学理论知识．如果在情境创设中设计变式训练,则学生学习的兴趣和积极性将会得到更大激发,而且其中的知识也会比单独的情境教学更加直观和更易理解,从而有效地帮助学生深度学习．

在圆锥曲线教学时,双曲线的定义和标准方程与椭圆很类似,学生已有学习椭圆的一些经验,怎么由椭圆的定义自然过渡到双曲线的定义？可设计教学(片段)如下.

复习椭圆的定义．

探究与拓展用圆规画一个圆O,然后在圆内标记点A,并把圆周上的点P1折叠到点A,连结OP1标记出OP1与折痕l1的交点M1(如图2),若不断在圆周上取新的点P2,P3…，进行折叠并得到标记点M2,M3…则点M1,M2,M3…形成的轨迹是什么?并说明理由.

变式当定点A在圆外,此时形成的轨迹是什么?

题目的本质就是到两定点的距离之和是定值,过渡到两定点距离之差的绝对值是定值，从而得出相关点的轨迹是双曲线．

变式思维与情境教学结合在一起可以更

好地展示数学知识的相通性,同时也可以更好地启发学生思维,深度挖掘数学知识的内涵,从更深的层次理解知识．

变式教学是数学深度学习中重要的内容．通过变式训练的方式,让学生掌握知识的本质,在解决问题的过程中发现复杂问题背后的属性,进而有效提升学习效果的同时,帮助学生建立更加优良的数学思维．

数学学科核心素养是数学方法的集中体现,在数学概念教学设计中,要充分关注数学学科核心素养的达成;要深入理解数学学科核心素养的内涵、价值、表现、水平及其相互联系;要结合特定教学任务,思考相应数学学科核心素养在数学中的孕育点、生长点[3]．深度学习下的数学概念课设计，为教师提供了课堂变革的基本思路和原则,有助于提高教师的专业素养,使教师能够精准设计每一堂课教学．基于深度学习的教学设计，在围绕理解数学、理解学生、理解教学下开展,遵循学科特点,找准数学学科价值引领的支撑点,关注数学学科目标在教学中的可实现性．同时，深度学习是内源性学习,需要给予学生充分的指导和帮助,并为他们营造出更多的自主解决、分析知识以及问题的环境,进而让学生的综合素养水平得到有效提升．