技术增强型学习环境下的灵活思维：量表的本土化研究及应用

赵亚如 李朝乾 陈云红 李书明

一、前言

创新人才培养是我国建设创新型国家的关键步骤。《中国教育现代化2035》明确提出“新时代教育需创新人才培养方式，培养学生创新精神与实践能力[1]”，创新思维与创新能力的培养已成为当前教育领域关注的重点问题。灵活性是创新思维的三大基本特征之一，是指个人面对问题情境时，能够灵活处理、随机应变，不墨守成规[2]。《21世纪教学技能与评估框架》将灵活性作为思维方式培养的主要部分，并提出受教育者将会具有灵活的思维能力以及适应新的学习方式和交流方式的能力[3]。灵活思维的培养是创新型人才培养的重要步骤。

互联网、大数据等新兴技术的迅猛发展正在改变着人们的学习习惯和方式，大量的学习管理平台、学习工具以及智慧学习环境的开发与应用都表明，当前已进入技术增强型学习环境[4]。国外研究认为，技术增强型学习环境是基于信息技术的，以数字化学习资源的丰富性和可获取性、学习工具的可移动性和可交互性、学习支持服务的智能化和个性化、学习空间的开放性和虚实融合为主要特征，旨在为学生信息化学习赋能，促进学生有效学习、与传统学习环境相对的一种新型学习环境[5]。

随着教育技术的不断更新和学习环境的不断变化，众多学者呼吁，应基于新型学习环境，创新灵活思维的内涵及评价标准，以适应当代教育领域的发展[6]。而目前国内研究者更多关注基础教育领域的创造性思维[7]、批判性思维[8]等思维方式的培养，对灵活思维的关注相对较少，且尚无较成熟的灵活思维评价工具。Miri Barak等人在对灵活思维进行重新定义的基础上，开发了技术增强型学习环境下灵活思维量表（Flexible Thinking in Learning Scale,FTL），并证实了FTL量表的内容、结构和同时效度（concurrent validity）[9]。目前，作为一项新型教学环境下专门评估和预测学习者灵活思维能力及倾向的测评工具，FTL量表在西方背景下的适用性和有效性已得到了检验[10]，但在我国文化背景下的应用尚未出现。因此，本研究将引进FTL量表，对其进行本土化，并基于现代测量理论，重点探究FTL量表中文版的测量学特性和大学生的灵活思维特点，以期为高校创新人才及思维能力培养的相关研究提供参考。

二、研究设计

（一）研究工具

为应对当前的技术变革和教育挑战，以色列学者Miri Barak等将技术增强型学习环境下的灵活思维概念化为一种包含开放思维的高阶思维技能，并将其作为学习者适应学习情境变化、接受新的不断变化的技术的能力基础，结合技术接受模型（Technology Acceptance Model）[11]、开 放 思 维 问 卷（Open-Minded Thinking Questionnaire）[12]和个体适应量表[13]（I-ADAPT Scale）编制了FTL量表。

FTL量表从3个维度、17个项目对学生在技术增强型学习环境下的灵活思维能力及倾向进行评价，分别是：（1）对学习技术的接受度（Learning Technology Acceptance，TA），即适应先进技术并有效地利用它们进行有意义学习的能力，共5个项目；（2）学习中的开放思维（Open-mindedness in Learning，OM），即学习他人能力、管理团队合作精神、倾听多种观点和处理复杂问题的能力，共7个项目；（3）对新的学习情境的适应度（Adapting to New Learning Situations，AL），即找到多种解决方案、解决不熟悉问题以及将知识迁移到新情境中的能力，共5个项目，所有项目均采用李克特六点式计分。Miri Barak测量的量表整体信度为0.91，信度良好。其研究结果同时证实了FTL量表的内容效度、结构效度、并发有效性以及跨群体和随着时间推移的稳定性，表明FTL量表是一个良好的灵活思维评估工具。

（二）研究方法

量表的本土化研究是依据Brislin经典翻译模型实现的，经过对原量表的翻译、回译与专家咨询，形成最终的FTL量表中文版。量表的测量学特性检验以多元概化理论和经典测量理论为理论依据。首先应用多元概化理论进行量表的信度检验，并提出优化策略；之后应用经典测量理论检验量表的内容效度和结构效度，分别通过皮尔逊相关分析、条目分析、探索性因子分析（Exploratory Factor Analysis，EFA）和验证性因子分析（Confirmatory Factor Analysis,CFA）实现。数据的处理与分析主要通过mGENOVA2.1、SPSS24.0和AMOS软件实现。

（三）研究对象

分别抽取华中地区H大学文史类和理工类专业一至四年级本科生参与本次研究。问卷以线上方式统一发放，共发放问卷500份，回收492份，问卷回收率98.40%，其中有效问卷473份，有效率96.14%。样本人口统计变量见表1。

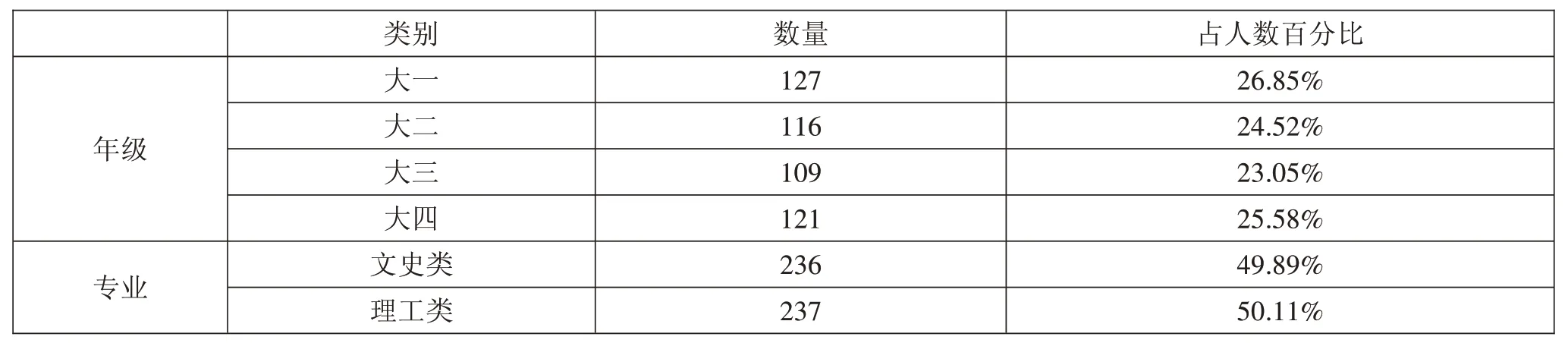
表1样本人口统计变量的描述性统计

三、研究结果

（一）量表的本土化

本研究依据Brislin经典翻译模型[14]，依次经过对量表的翻译、回译以及专家咨询，形成最终的FTL量表中文版。（1）翻译：邀请1名具有中英背景的教育技术学博士与1名专业英语八级的教育学博士组成翻译小组，采用独立翻译的方式，将FTL量表翻译为中文，之后将两位博士翻译的FTL量表中文版本进行综合讨论，形成一个中文版量表。（2）回译：邀请1名专业英语大学教授，在对原版FTL量表未知的情况下，将中文版量表回译为英文。（3）专家咨询：邀请1名教育技术学专业教授将回译的英文版量表与中文版量表进行细致的比较、分析，并与进行翻译和回译工作的博士和教授进行讨论。

对中文版量表内容进行修改和语句的本土化调整。如条目5“I like to experience new learning technologies”翻译为“我喜欢体验新的学习技术”，专家认为“体验、学习技术”的表达不够清晰、准确，将其修改为“我喜欢尝试新的助于学习的技术”。条目11“For deep learning，I tend to examine diverse viewpoints”翻译为“对于深度学习，我倾向于检查各种观点”，专家认为“倾向”不够具体，可能会影响学生的自我判断，将其修改为“为了实现深度学习，我经常仔细检验各种观点”。“Adapting to new learning situations”维 度 中 的“learning situation、learning condition”统一翻译为“学习条件”，专家认为学习条件的概念不够具体，不能区分出学习环境和学习情境，因此将条目中的“learning situation”翻译为学习情境、“learning condition”翻译为学习环境。最终形成的FTL量表中文版见表2。

表2 FTL量表中文版

（二）基于多元概化理论的量表信度分析

多元概化理论（Multivariate Generalizability Theory，MGT）可以看作是概化理论（Generalizability Theory,GT）的延伸，概化理论是在经典测量理论（Classical Test Theory，CTT）基础之上发展起来的现代测量理论[15]，其基本原理是运用实验设计的思想，采用方差分析的方法来全面估计各种方差成分的相对大小，包括主效应和交互效应，并能对各估计值的大小进行直接比较。

在概化理论中，估计各方差成分相对大小的过程，称为概化理论的G研究；G研究的下一个阶段是D研究，即通过实验研究，进一步考察不同测验设计条件下概化系数的变化状况（如试题容量变化对于概化系数的影响），从而寻找能够控制误差的最佳方法，作出最佳的设计决策[16]。概化理论对测量误差变异的构成提供了多个维度的视角，但只能实现单变量测量信度的分析。多元概化理论与概化理论的方法构架相同，是对GT的推广和发展，便于深入研究测量目标由多个变量组成的问题（如总测验可以分解为多个不同维度的分测验）[17]。近年来，基于这一理论的研究设计已应用于教师资格证考试、普通话考试、高考等大规模测验，拓宽了常模参照测验和标准化测验的信度检验方式。

1.G研究

FTL量表由3个分量表（技术接受度、思想开放度、环境适应度）组成，可视为包含3个分测验的综合测验，因此研究设计可以设定为涉及3个潜在因子的p×i随机单面交叉设计（p表示被试，i表示量表项目）。根据多元概化理论的数学模型，可编写一个包含3个分测验的mGENOVA程序进行G研究，以估计不同误差来源的方差比例，评价各分量表对总测验的贡献程度。G研究结果如表3所示。

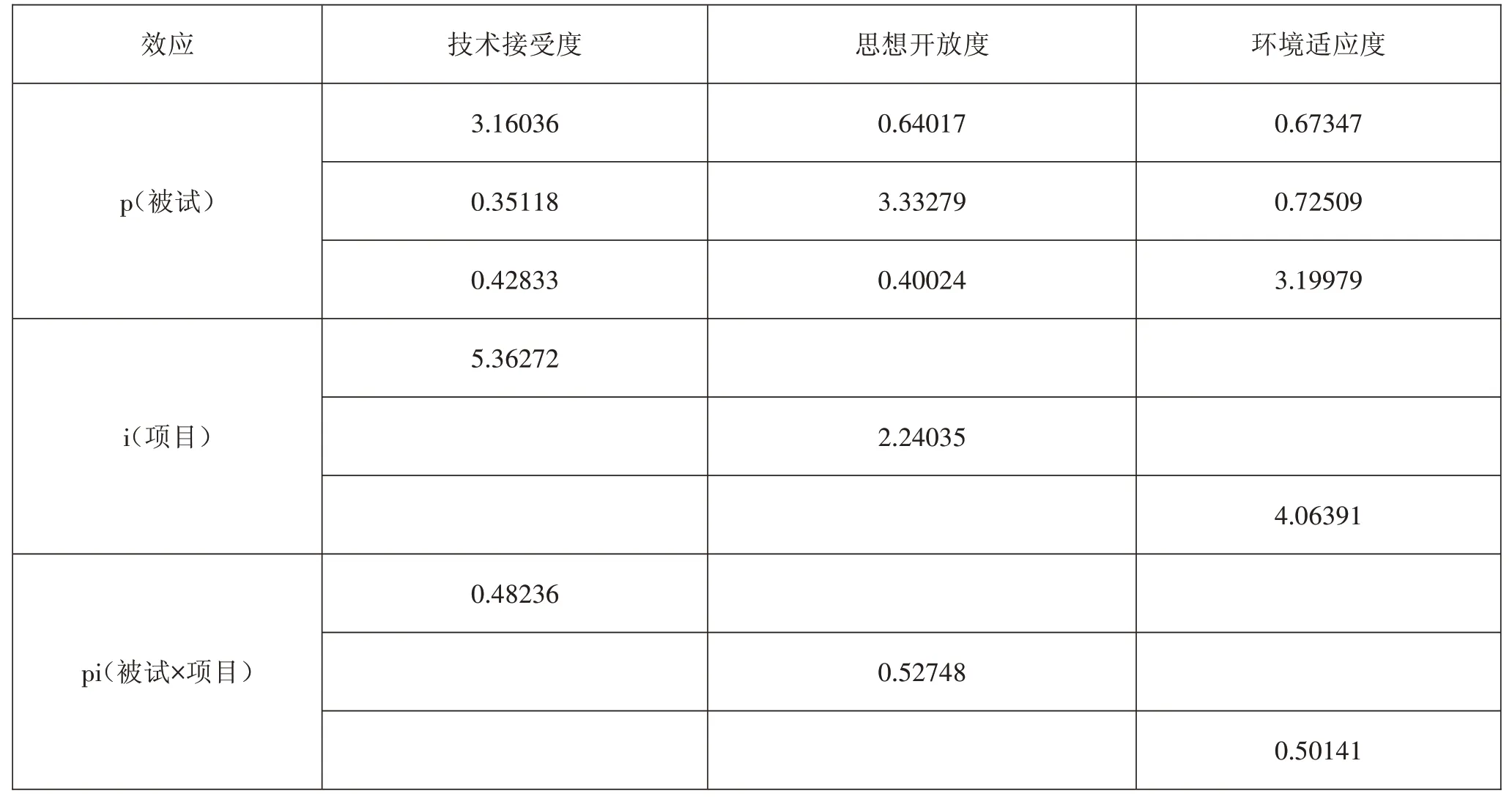
表3 G研究中各效应在三个分因子上的方差与协方差分量估计矩阵

多元概化理论认为，一项测验中被试效应（及测量目标）所占的方差分量比例应为最大，其他效应则均被看作是测量侧面，并要求它们应尽量占更小比例的方差[18]。通过表3数据可知，仅有思想开放维度的被试效应方差分量估计值高于其余效应（3.33279>2.24035>0.52748），技术接受和环境适应维度的被试效应方差分量均低于项目效应的方差分量，表明思想开放维度的项目质量最高，能有效测量出学生开放思维之间的差异。在项目效应中，技术接受维度的项目分差分量最大（5.36272），其次为环境适应维度（4.06391），表明这两个维度的项目区分度略低。进一步分析协方差分量和相关性，发现被试在三个分量表间的协方差分量偏小（均小于0.5），但在三个分量表间的相关系数较大（均大于0.6）。以上表明，将三个分量表的测验得分进行合成是可行的，各分量表项目本身所占的方差分量较大，而被试与项目的交互效应很小，可以认为FTL量表适宜作为常模参照性测验使用。

2.D研究

为探索各分量表及总体对测量总分可靠性的贡献程度，进行P×I三因子随机单面交叉设计的D研究。根据G研究估计的方差与协方差矩阵，可以进一步估计被试在各分量表及总量表上的全域分数以及相应的误差估计的方差分量，进而估计概化系数与可靠性指数，D研究结果如表4所示。

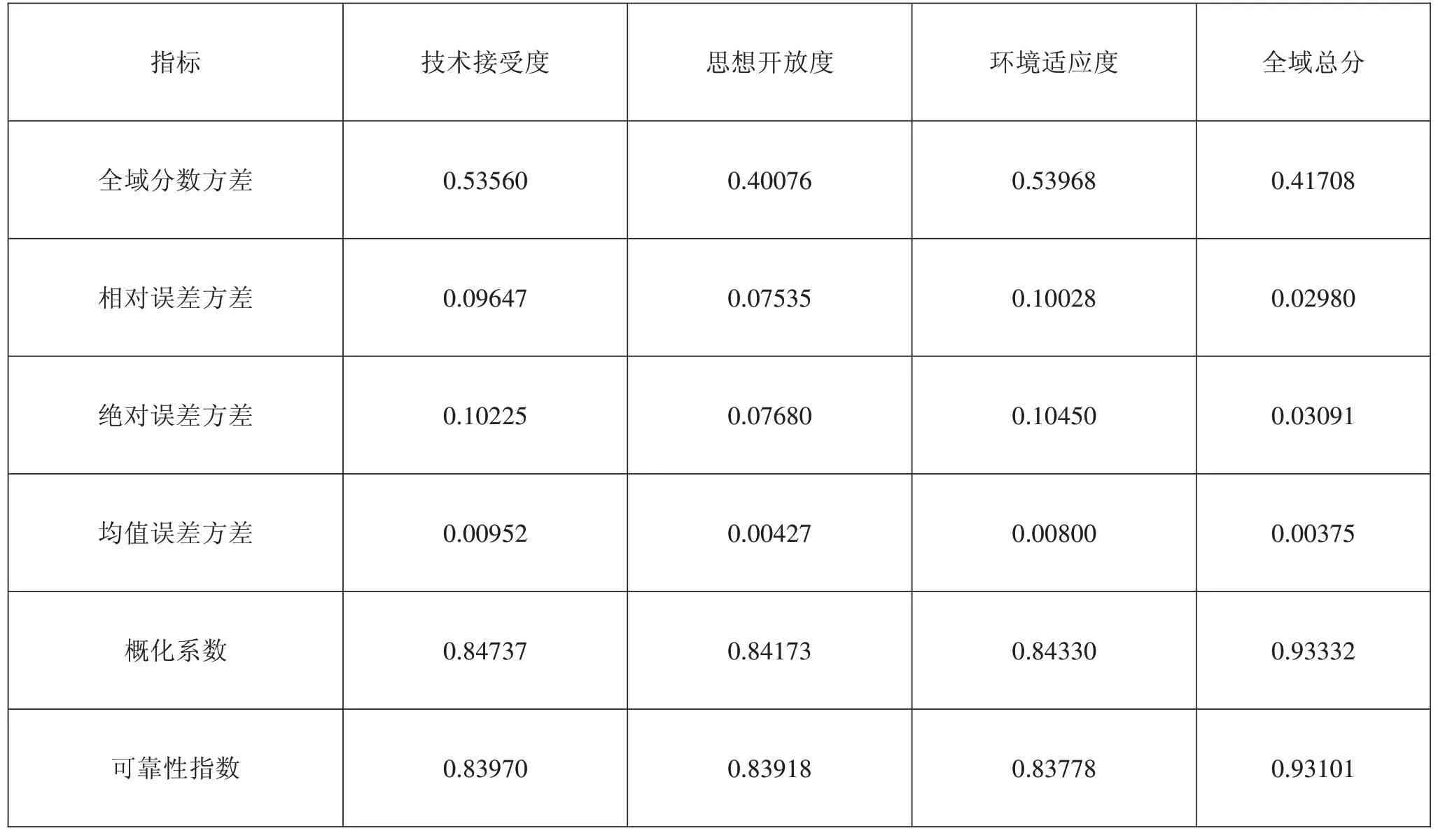
表4全域分数等在各因子上估计的方差分量值（D研究）

由表4可知：环境适应度分量表的全域分数方差、相对误差方差以及绝对误差方差分量均最大，说明该分量表的信度较低；技术接受度的均值误差方差最大，表明本次测验中，该分量表的一致性最低；从概化系数和可靠性指数两个方面看，3个分量表的信度均达到较好水平（概化系数和可靠性指数均大于0.8），FTL总量表的概化系数和可靠性指数均高于各分量表（大于0.9），这表明将FTL以整体进行测验时信度最高，测验效果最好，既可作为常模参照性测验，也可作为标准参照性测验。

3.提高测量信度的D研究

为进一步改进测量信度，本研究考察了各分量表样本容量变化对FTL总量表概化系数的影响情况，结果如表5所示。由表中数据可看出，FTL总量表的概化系数随着各分量表样本容量的增加也逐渐增大，但当概化系数增量达到极值后，其增加幅度也逐渐减小。仔细观察数据可发现，在结合研究成本等条件下，技术接受度分量表的样本容量为7、思想开放度分量表的样本容量为12、环境适应度分量表的样本容量为7时，FTL量表总体的概化系数和测量效果最理想。

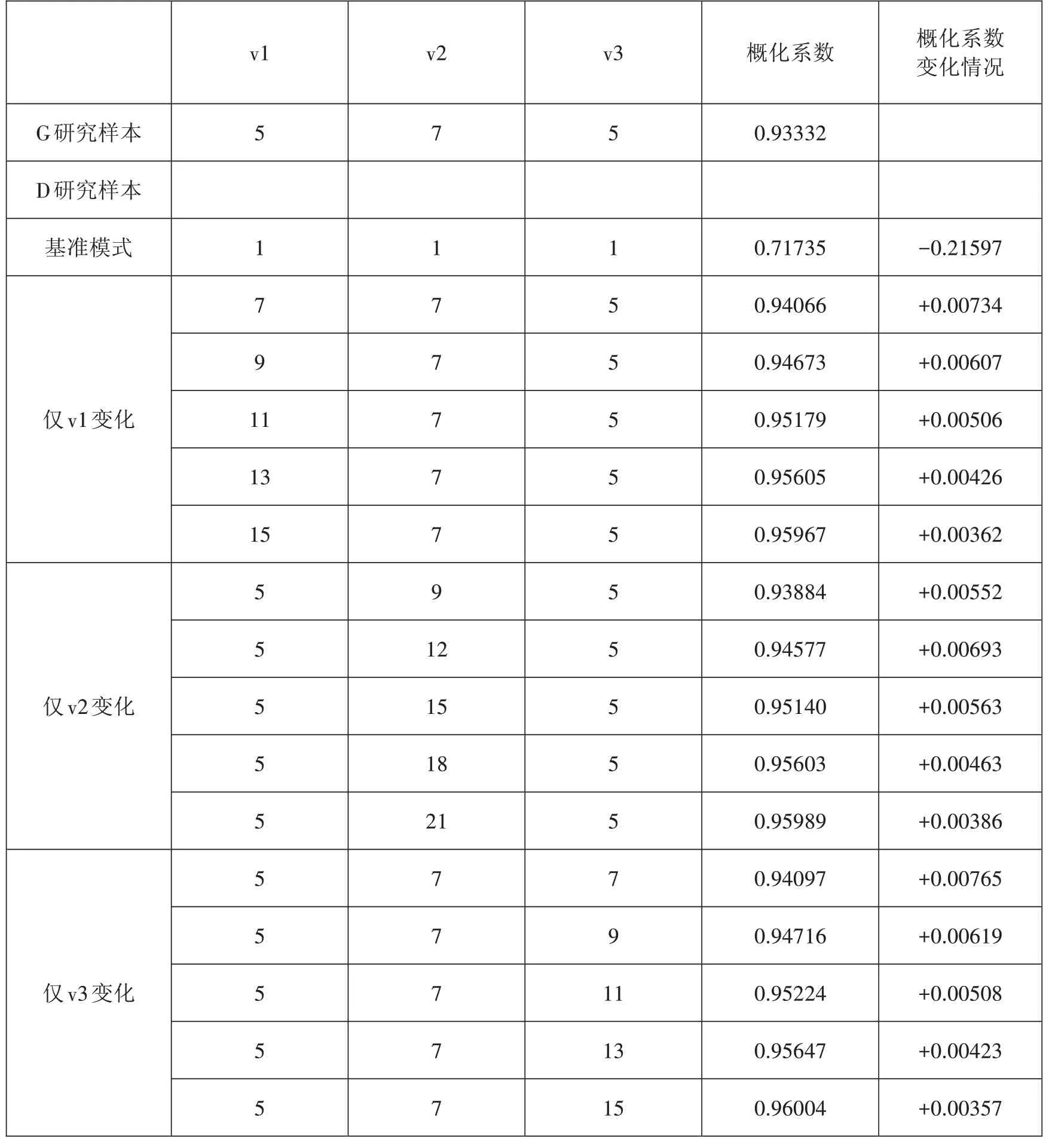
表5样本容量对FTL总量表的概化系数变化（D研究）

（三）基于经典测量理论的量表效度分析

概化理论弥补了经典测量理论信度分析的缺点，实现了误差来源的精准分析和量表优化，但经典测量理论提出的效度分析方法仍是应用最为广泛的[19]，因此本研究将应用经典测量理论对量表的内容效度和结构效度进行分析，以检验量表对大学生灵活思维能力及倾向的真实反映程度。

1.内容效度

采用极端组法和皮尔逊相关分析法检测该量表条目的区分度。将473份有效问卷中的17个条目总分按降序排列，选取总分≥83分（前27%）为高分组，将总分按升序排列，选取总分≤68分（后27%）为低分组。

对高分组和低分组进行独立样本t检验，结果显示，高分组和低分组每个条目得分比较差异均有统计学意义（P<0.01），95%的置信区间未包括0，说明条目具有较高的鉴别度。进一步进行条目得分与总分之间的相关性分析，结果显示，各条目得分与总分的Pearson相关系数为0.379~0.870（P<0.01），说明量表各条目具有良好的鉴别度，内容效度良好。

2.结构效度

运行SPSS软件，对量表进行探索性因子分析，以实现对量表效度的检验。首先进行KMO检验和巴特利球体检验。借助最大方差法，进行分量矩阵的旋转，结果显示，KMO值为0.916（数值越接近于1，变量间的相关性越强，偏相关性越弱，因子分析的效果越好），表明适合进行因子分析；Bartlett’s球形检验值x2=1453.569，P=0.000，表明各变量间具有相关性，因子分析有效。其次，使用主成分分析法进行方差最大旋转，来实现公共因素的提取，共提取特征值>1的公因子3个，旋转后特征值分别为3.653、3.335、3.266，可解释结果的60.316%，各公因子负荷量见表6。

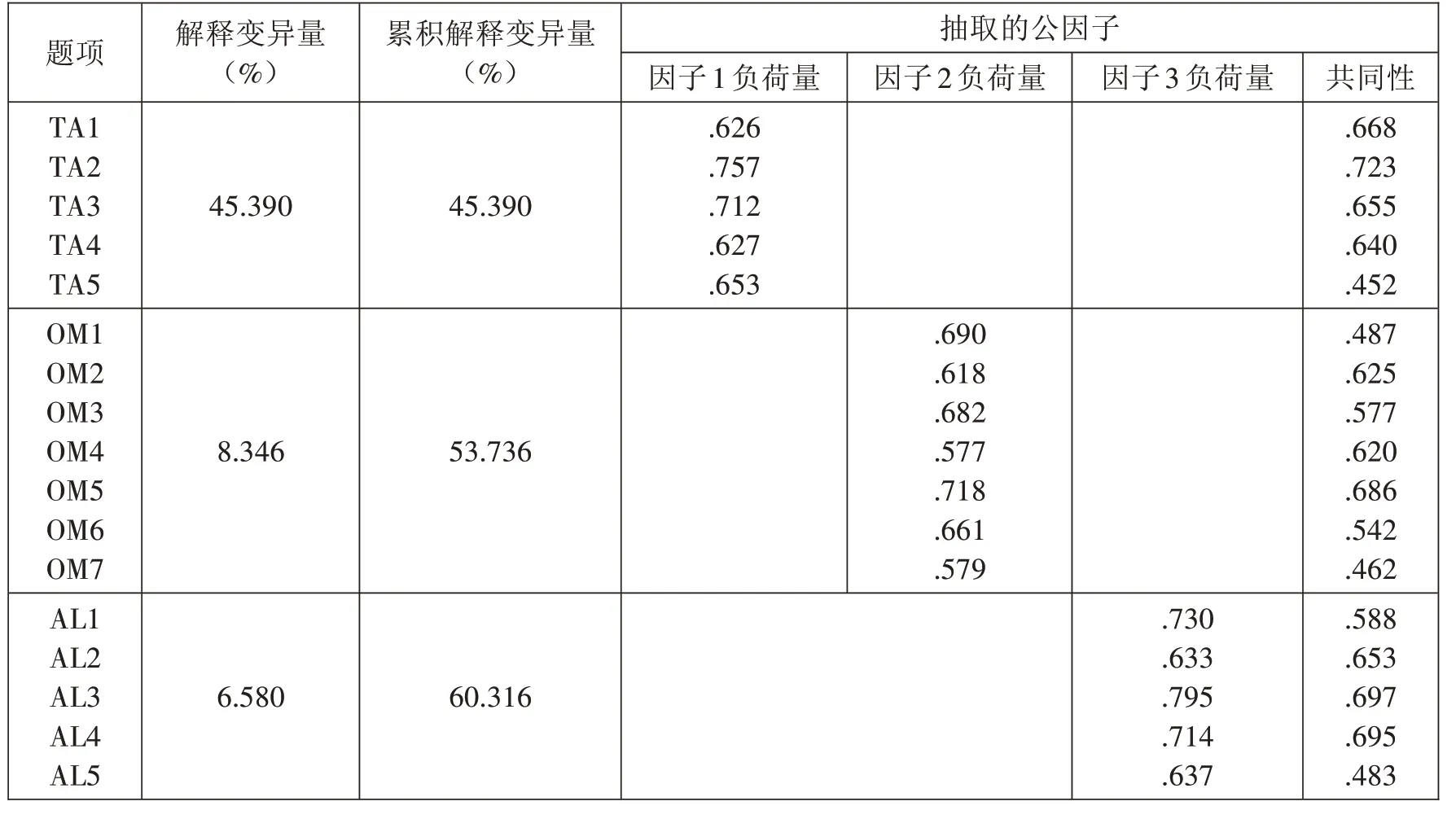
表6 FTL量表各维度在各公因子的负荷量

运行AMOS软件，进行验证性因子分析，以实现量表的结构方程模型检验。将数据导入，运行软件得到结构方程模型（见图1）及相应拟合指数（CFI的值为0.964、IFI的值为0.965、NFI的值为0.901、GFI的值为0.911、RMSEA的值为0.054、CMIN/DF的值为1.490）。其中，CFI、IFI和NFI是增值拟合指标，其值介于0和1之间，越接近1，则模型与数据之间的拟合度越好，模型拟合度越高；GFI、RMSEA、CMIN/DF为绝对拟合指数，GFI的值大于0.9为可接受范围；RMSEA的数值越小越好，CMIN/DF数值<3则表示模型的适配度好。将结构方程模型的拟合指数与模型的分析值进行比较，可知，模型与数据的拟合度较好，适配度较高，符合“既简单拟合度又高”的模型标准。

（四）FTL量表中文版的应用分析

为探究FTL量表中文版在大学生群体中的应用效果，本节将分别对被试的灵活思维总体水平、差异性及相互关系展开分析。

1.描述性统计分析

为研究被试样本的灵活思维整体水平，对收集的有效数据进行描述性统计分析。数据显示FTL量表中文版的平均得分为M=4.45，SD=0.74，学习中的开放思维平均得分最高(M=4.55，SD=0.75)，学习技术接受度平均得分为M=4.47，SD=0.86，适应新学习情境的平均得分为M=4.31，SD=0.86。进一步统计发现，有50.74%的被试在FTL量表中文版上得分大于4.45，有53.91%的被试在学习中的开放思维上得分大于4.55，有49.68%的被试在学习技术接受度上得分大于4.47，有50.32%的被试在适应新学习情境上得分大于4.31。

这表明参与调查的被试样本中，有超过一半的学生更倾向于听取不同的观点和观点，而很少倾向于重复做同样的事情。然而，仍有很大比例的大学生对灵活思考的倾向较低，对抵制技术变革的倾向较高，尤其表现在对新技术的接受度上。

2.差异性分析

为探究被试在不同条件下的灵活思维差异性，分别以年级和专业为分类标准对其差异性进行了分析。结果显示，FTL总分、学习技术接受度和适应新学习情境维度在年级上的差异显著性均为0.000，达到极其显著水平，开放思维的差异显著性最低0.001，为较显著水平；但在专业上不存在显著性差异。

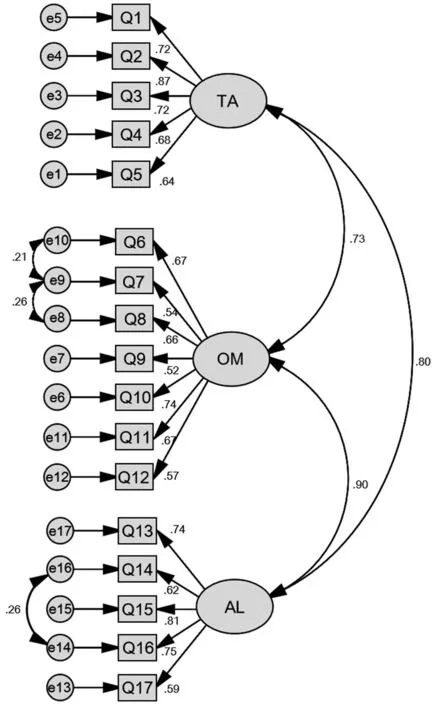
图1验证性因子分析模型图

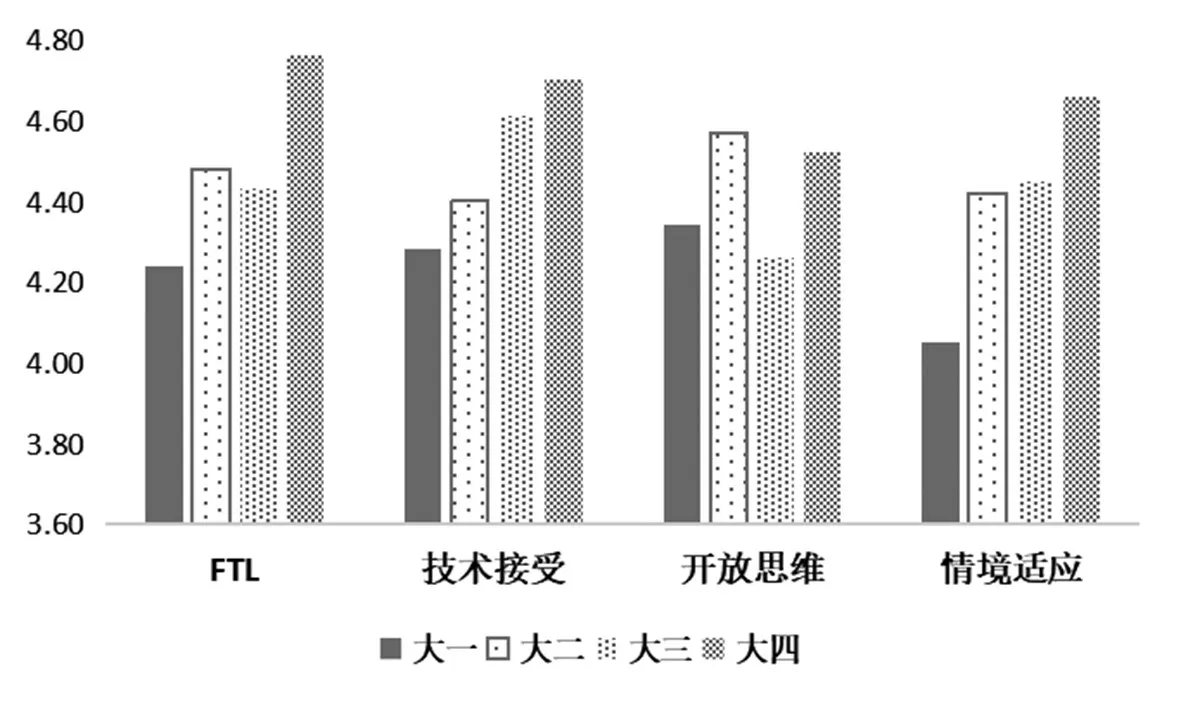
图2不同年级灵活思维均值情况

进一步统计各维度在年级上的差异水平，得到如图2所示的柱形图。由图2可看出，从年级层面来看，二三年级的整体水平无显著差距，一年级与四年级之间存在较大差距，尤其表现在新的学习情境的适应度方面，部分大一新生表示自己在适应新的学习情境和学习方式时存在困难，但表示可以通过个人努力使自己适应学习方式的变化；在开放思维方面，各年级之间差距不大，但平均水平较低（均低于4.55）；在对学习技术的接受度方面，表现出随年级递增的现象。

3.相关性分析

一般认为，两变量的相关系数绝对值在0.8-1.0之间时为极强相关，相关系数绝对值在0.6-0.8之间时为强相关，相关系数绝对值在0-0.2之间时为极弱相关，而相关系数的正负则分别表示两变量间的促进与抑制作用。

首先,对灵活思维各表现水平（因变量）进行相关性分析，结果见表7。由表中数据可发现，各表现水平之间都存在显著的强相关性（p<0.01，r>0.6），其中灵活思维总水平与各维度表现水平均呈现出极强程度的正相关关系，但与开放思维表现水平的相关性最强（r=0.904）；各维度之间的相关程度为强相关，其中开放思维表现水平与新学习情境适应水平之间的相关系数最高（r=0.725）。

其次，将学生的学习成绩与灵活思维总水平进行了双变量相关分析，结果显示两变量间呈显著极弱相关（r=0.183，p<0.05）。综合上述分析结果可发现，大学生的灵活思维水平与其学习成绩间存在显著但极弱的相关性、与开放思维间存在显著且极强的相关性，学生的开放思维水平与新学习情境的适应水平存在显著而强的相关性，表明开放思维与灵活思维之间具有极强的直接促进关系，新情境的适应水平可以较准确地反映开放思维水平，大学生的学习成绩与灵活思维之间的促进关系极小可忽略。

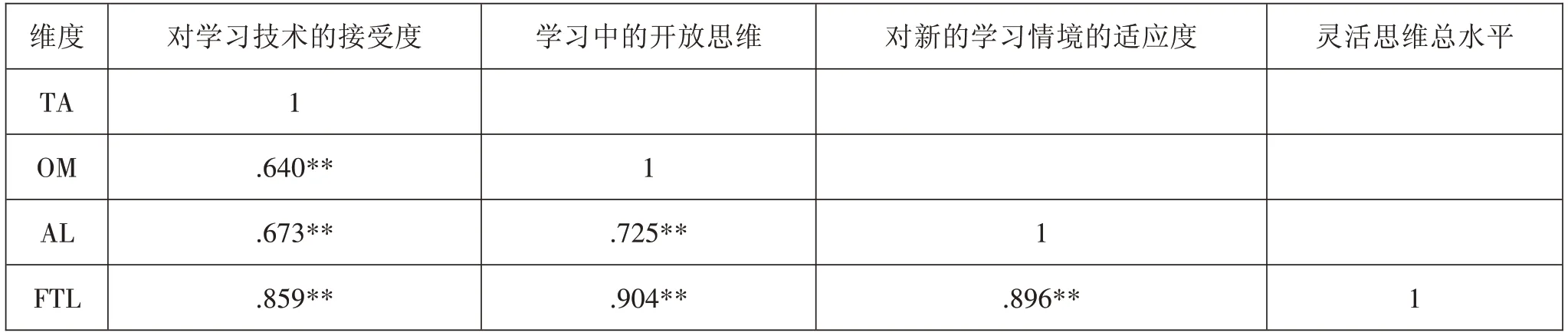
表7灵活思维各水平相关分析表

四、研究结论

本研究为两个部分，第一部分对FTL量表进行了六阶段的本土化研究，第二部分是对第一部分形成的FTL量表中文版的应用分析，得到的主要结论如下：

第一部分的量表本土化研究前两个阶段主要是FTL量表的翻译与回译。主要对“learning situations”与“learning conditions”处作了修改，在考虑学习情境与学习环境的界定范围后，将第三个维度的相关概念统一设定为“学习情境”。

第三、第四阶段主要是应用多元概化理论进行FTL量表中文版的信度分析和改进优化。通过G研究结果可以发现，被试在三个分量表上的方差分量占比均等，与各分量表的项目数量占比相同，符合多元概化理论中权系数的设计。从协方差分量和相关系数上看，3个分量表间的一致性和相关性较大，可以将三个分量表的测验得分进行合成。此外，在方差贡献率上，项目效应在技术接受度和环境适应度2个分量表所占的方差分量均最大，表明这两个分量表的测验项目有较好的区分度。D研究结果显示，FTL量表汉化版的整体信度较高，且高于各分量表的概化系数和可靠性指数，环境适应度分量表的误差分量最大，可进行适度优化调整。而后，从调整项目侧面的样本容量角度进行了D研究，发现增加样本容量能有效提高量表的信度，但随着样本容量倍数的增加，其信度的增势呈现减缓趋势，因此少量增加各分量表的项目数量能够最大限度地增大量表的整体信度。

第五、第六阶段主要对FTL量表中文版进行了效度分析。在第五阶段运用极端组法和皮尔逊相关分析检测了量表项目的区分度，结果显示各项目均具有较高的鉴别度且呈现显著正相关。第六阶段通过探索性因子分析（EFA）和验证性因子分析（CFA）检验了中文版量表的结构效度，并构建了良好的拟合模型。结构方程模型表明，学生接受先进技术的能力、适应新的学习环境的能力和其开放性思维之间均具有显著的正向相关性，其中学生的开放性思维与新环境的适应度之间的相关关系最显著。此外，在标准化的情况下，指标与潜变量之间的复相关系数就是因子负荷的平方。本模型中三个潜变量，即技术接受度（TA）、思想开放度（OM）和环境适应度（AL）在17个观测指标上的标准化因子不小于0.708的有8个，因此，有8个复相关系数大于0.5，即三个潜在因子变量能解释项目的50%以上，模型的解释能力良好。

第二部分的FTL量表中文版实践应用分析是以473名本科生为研究对象，从描述性、相关性、差异性三个方面展开量化研究。

通过描述性统计分析发现，被试的FTL量表中文版平均得分为4.45，且有超过一半比例的被试达到了平均水平。灵活思维的三个维度中，学习中的开放思维平均得分最高，达到该维度平均水平的学生数量也是最高的（53.91%），但在新技术接受维度上达到平均水平的学生数量未超过一半。表明该样本中有超过一半的被试具有开放的思维，倾向于听取不同的观点，而很少倾向于重复做同样的事情，但有很大比例的被试不能快速适应新的学习技术。

在差异性分析中发现，被试群体表现出年级上的极其显著差异性，在开放思维维度的差异性表现最低，但在专业上未表现出显著的差异性。一至四年级学生的灵活思维呈现出随年级阶梯递增的现象，一年级学生在对新的学习情境的适应方面水平较低，四年级学生在整体水平上表现出明显的优势，但各年级学生的开放思维水平均需提高。

在相关性分析上发现，FTL总水平与各维度间均存在显著正向相关性，学习中的开放思维与灵活思维的相关系数最大（0.904），而学习中的开放思维与对新学习情境适应性维度的相关性最显著，因此可从培养学生倾听他人不同观点以及表达个人观点方面培养学生的开放思维，从提升学生的信息意识、信息素养及信息交流能力方面促进学生对新的学习情境的适应度，进而培养学生的灵活思维。

综上所述，FTL量表既是一种研究工具，也是一种自我评估工具。它可以有助于评估学习者灵活思考的性格倾向，或帮助解释关于使用新的学习方法或新技术的个人差异。本研究依据Brislin经典翻译模型形成了FTL量表中文版，并进行了信效度检验和实证分析，结果表明中文版量表整体的信度较高，增加项目数量可进一步提高信度系数，内容效度和结构效度良好，当前大学生的灵活思维处于中等水平，且存在年级上的差异。

由于本项研究的样本只涉及一所高校的本科生，因此尚不能验证FTL量表中文版在各类学习者上的稳定性与一致性。未来与FTL相关的研究还可专注于教学干预对学习者灵活思维的影响程度以及灵活思维与协作学习之间的关系等方面。