基于支持向量机的阅读理解试题难度预估研究

吴生蕾 任 杰

一、引言

阅读理解是语言测试的考查重点，把握阅读理解试题的难度有利于平衡语言测试的整体难度。根据影响因素不同，难度可分为相对难度和绝对难度[1]。绝对难度由试题本身决定，而相对难度来源于试题与考生两个方面：源于试题本身的难度，影响因素主要有知识点、问题情境、提问方式、试题考查的学生的认知层次等；源于考生的难度，影响因素主要有考生群体的能力水平、教师的教学方法等。因不步及对考生群体的研究，本文中阅读理解主式题的难度指绝对难度。

对于阅读理解试题来说，题目难度来源于阅读文本与题目设置两方面。阅读理解测试研究专家奥德森认为，文本选择与题目设置对控制阅读理解试题的难度是同等重要的[2]。幺书君认为，HSK听力试题的难度受听力语料类型、试题题型、题目的提问方式与提问角度等因素影响，认为无情节和观点的听力语料难度较高；在题型上，判断题难度高于选择题；对具有概括性事物提问的试题难度较高[3]。阅读理解试题的题目材料与听力试题的题目材料有相似之处，二者都由成段的或成篇的文本材料和提问的题目构成。因此，与文本材料、题目设置影响听力试题的难度类似，文本材料、题目设置也影响阅读理解试题的难度。

许多学者从内容效度、阅读能力角度研究影响阅读理解试题难度的因素，前者主要包括对文本易读性、文本题材、话题、体裁等的研究。荆溪昱从文本的信息量、句法难度和语义难度角度提出适用于中文教材的易读性公式[4]。Drum等的研究表明，词汇频数、高频次与低频词数量、词汇认知、语法控制、具有迷惑性的选项、句子长度等因素对题目难度有重要影响[5]。王佶旻研究发现，文章的题材、题干类型与选项字数会影响试题难度[6]。

有研究者认为阅读能力的核心是“理解”，围绕“理解”从人们解答阅读理解客观题的认知过程入手，将对于不同认知对象且具有不同难度水平的阅读理解进行纵向分级。武永明将阅读能力从低到高分为四种，分别是最基本的认读字词句的能力、理解主要内容的能力、进行评价鉴赏的分析能力以及要求最高的创造运用能力等[7]。杨帅将阅读能力由低到高分为四个等级，将题目对考生阅读能力的要求作为试题难度的影响因素[8]。

由于计算机具有非常强大的运算大数据的能力以及较高的运算速度，能够高效地分析处理数据并挖掘数据的潜在规律，1995年，Perkins等学者使用人工神经网络构建试题难度的预测模型，将机器学习算法引入了试题的难度预估领域[9]。在阅读理解测试方面，韩菡对汉语水平考试中的阅读理解试题进行了难度预估研究，使用BP（Back Propagation，反向传播）神经网络建立了试题难度的预估模型；研究结果显示，预估难度和实测难度在0.01水平下显著相关[10]。付佩宣使用BP网络模型，将选取出的实用汉语水平认定考试阅读理解题目的难度影响因素作为训练网络的初始输入变量进行试验，之后增加输入变量继续进行试验，结果显示预估难度与真实难度的相关达到了0.61[11]。张玄采用朴素贝叶斯分类器对某考试的言语理解与表达部分进行了难度预估研究，其预估的准确率为64.5%，远超过专家预测的24.5%的准确率[12]。龚晨曦采用朴素贝叶斯和文本相似度方法进行了试题难度预估，得出基于以上两种模型的难度预估准确率均高于专家预估的准确率，相较于文本相似度模型，朴素贝叶斯模型的性能更好[13]。

本研究以难度预估为主题，将支持向量机的机器学习方法用于语言测试之中，选取了支持向量机的分类模型和回归模型对HSK初、中等的常规阅读理解试题进行难度预估。

二、支持向量机

在二维平面中，将两类样本点划分开来的是一条线，在三维空间中，将两类不同样本划分开的是一个平面，而在n维空间（n>3）中，这个将样本分类的平面被称为分类超平面。支持向量机（Support Vector Machines,SVM）是一种二分类的线性分类器，根据距离分类超平面最近的点，即支持向量计算两个类别间的最大间隔，建立分类超平面模型。它不仅能够为线性可分的原始数据构建线性分类器，也能够为非线性可分的原始数据建立线性分类器。

在许多分类任务的原始样本空间内，（类别）与（数据特征）之间的关系是非线性的，可能并不存在能将两个不同类别的样本正确划分的分类超平面，于是选择核函数定义一个高维特征空间，将非线性可分的数据映射到高维空间，使原始数据在高维空间变为线性可分，选择了不适合的核函数会导致分类模型的性能不佳。

径向基核函数、多项式核函数、sigmoid核函数以及线性核函数是四种较为常用的核函数，这四种核函数的表达式如下。

核函数的作用范围是由参数γ决定的。为了选择出合适的核函数，于是允许模型对部分样本的分类出现错误，以保证大部分样本点被更好地分类。因此引入惩罚因子与松弛变量两个参数，表示对模型犯错的容忍度。惩罚因子C为常数且C>0，C越大，则会要求更多的样本均满足约束条件。松弛变量（slack variables）ξ可以调节模型对误差的容忍范围，ξ越大，模型对误差的容忍越高。

三、实证研究

本研究的试题样本选自HSK初等、中等的八套试卷，由阅读理解第二部分的210道试题组成，包括试题的阅读材料、题干、选项以及题目的IRT难度参数等数据。本研究对210道试题的难度进行了类别与数值的预估，采用R-4.0.4软件进行数据处理和可视化分析。

（一）确定难度的影响因素

本研究从文本特征、题目特征两方面挖掘难度的影响因素。从以下几个方面进行HSK初、中等阅读理解试题的文本特征研究。

1.文本题材。考生的学科、背景知识影响其对阅读材料的理解程度，当试题的阅读文本选取了冷门的题材，就会对阅读的难度造成较大影响，因此本研究将文本题材分为10类，对语料进行了标注。

2.文本体裁。考生对不同体裁文章的阅读能力是不相同的，这与对特定体裁的阅读能力的培养和训练有关。HSK初、中等阅读理解阅读文本的体裁主要有记叙、议论、说明三种。

3.文本易读性。荆溪昱的易读性公式为：易读性=17.5255+0.0024X1+0.04415X2-18.3344X3（X1、X2、X3分别代表文章字数、文章句子的平均长度、文章中熟悉词语所占的比重）。因此，本研究确定了文本字数、平均句子长度和熟悉词比重等三个影响难度的因素。

在计算熟悉词比重时，首先借助NLPIRICTCLAS汉语分词系统对样本题目的阅读文本进行分词标注，之后对分词结果进行人工检查，参照HSK初、中等的考试词汇大纲对分词结果进行调整，最后借助自编程序计算HSK初、中等所应掌握的甲、乙、丙三个等级的词汇数量占总词汇数量的比重。

题目包括题干和选项，因此题目特征也应从题干特征与选项特征两方面考虑，包括以下几点：

1.题干对阅读能力的要求。本研究根据题干的提问，将题目对阅读能力的要求按照从低到高分为微观理解能力、整体感知能力、解释推理能力和评价鉴赏能力四个等级。

2.选项长度。选项字数越多意味着选项包含的信息越丰富，对题目难度以及答题所用的时间均有影响。

3.题目中熟悉词所占的比重。计算题干、选项中的熟悉词比重。

4.干扰项数量。当干扰项不符合题干要求但符合语料大意，或者干扰项的观点与人一般的逻辑思维习惯相一致时，会对考生产生迷惑，增加题目难度。

（二）支持向量分类模型的难度预估

1.对题目难度因素进行编码

通过对HSK初、中等阅读理解文本的分析，以200字为一个区间将阅读文本字数分为两个水平；以20个字符为一个区间将平均句长因素划分为三个水平；样本题目中，文本的熟悉词的比重均在60%以上，于是以10%为间隔将其分为四个水平。

对于文本因素的具体分类情况如表1所示。

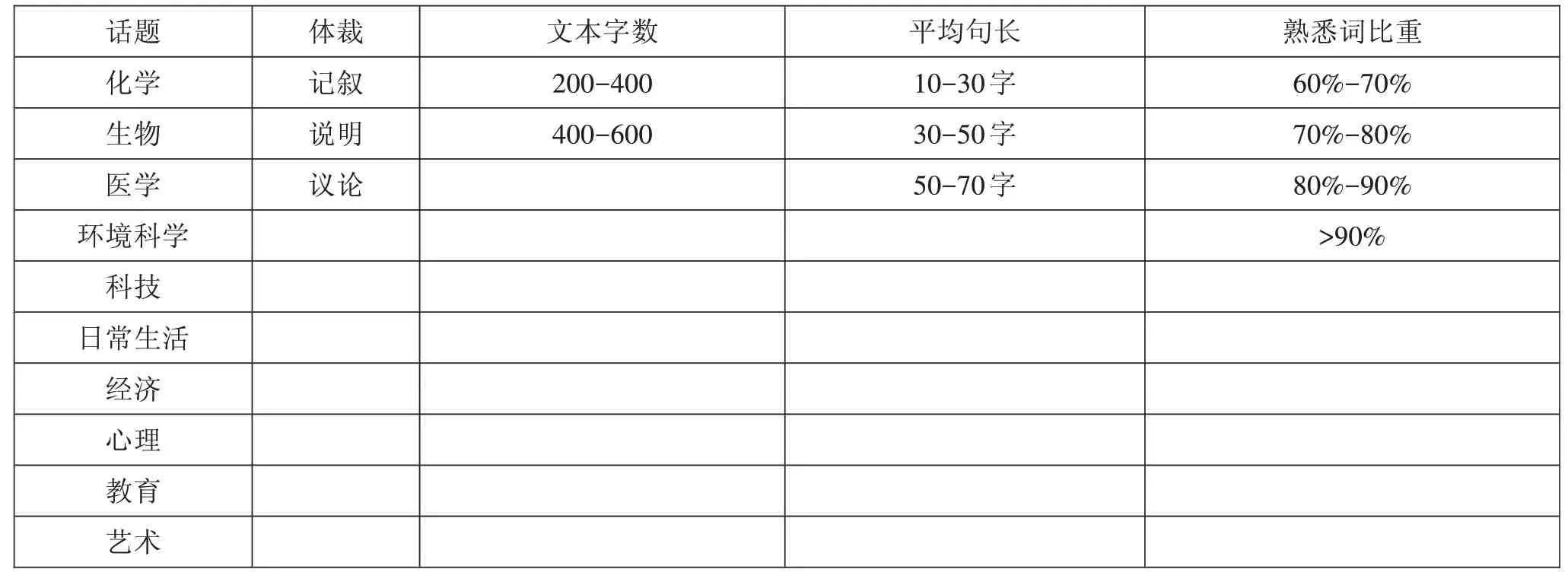
表1基于文本特征的难度影响因素编码表

通过对HSK初、中等阅读理解题目的分析，210个题目样本的熟悉词比重在30.77%~100%之间，由于熟悉词比重低于60%的题目数量极少，考虑到等级中的题目样本数量，将熟悉词比重在80%以下的试题分为一个等级，并以10%为区间将熟悉词比重在80%以上的部分分为两个等级；以16个字符为一个等级，将选项长度分为三个等级；将选项中符合阅读文本大意的或者符合人的思维习惯的错误选项作为干扰项，干扰项的数量有0、1、2、3四种。表2是基于题目特征的难度影响因素的编码表。

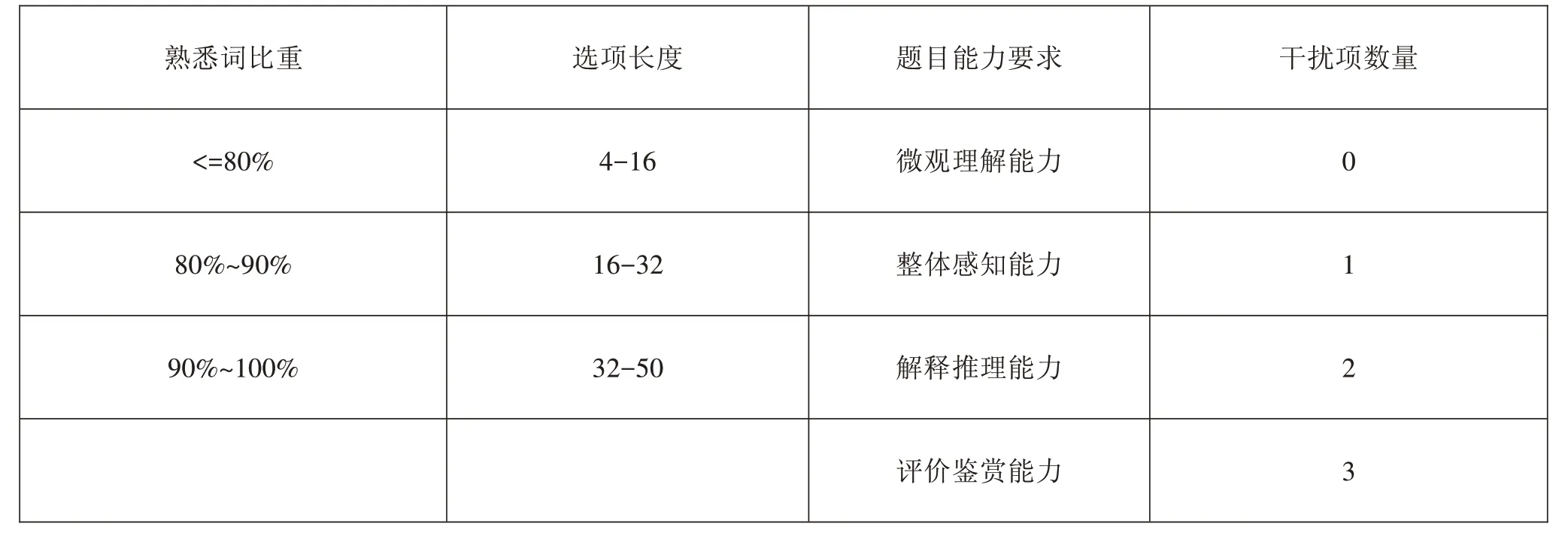
表2基于题目特征的难度影响因素编码表

本研究使用基于IRT模型的难度值，为了控制各难度类别中题目数量差异对模型效果的影响，将试题难度按照题目数量划分四个等级，使各等级的题目数量尽量接近，并且考虑等级临界处的题目难度值，确保各等级的题目难度值不相同。划分结果见表3。

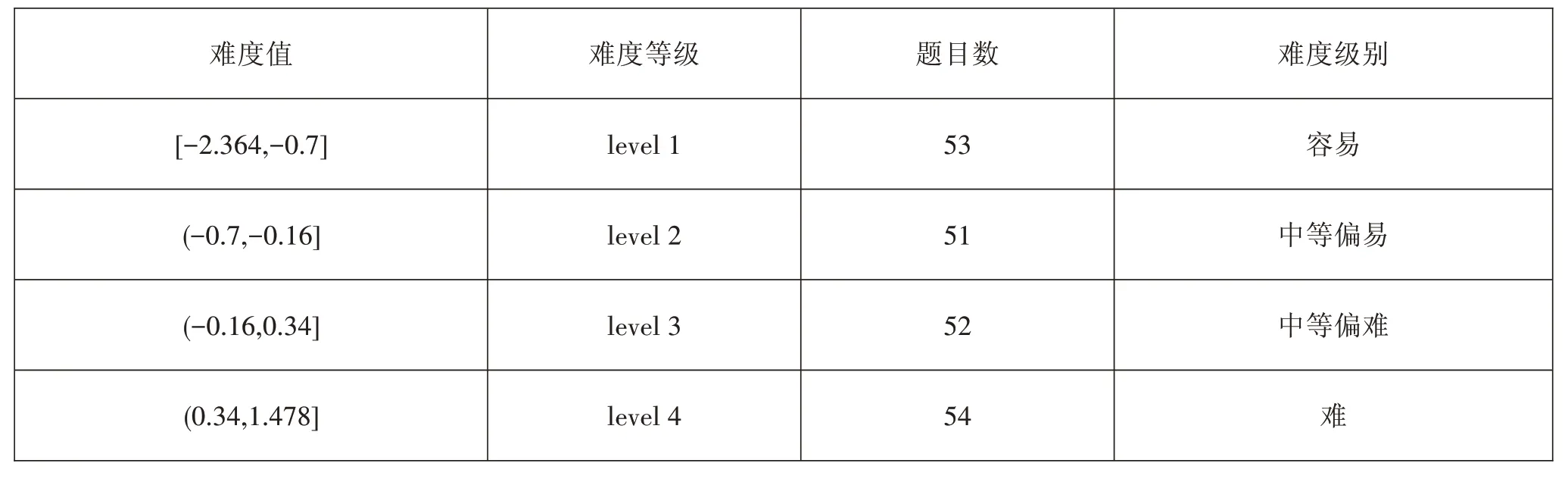
表3 根据题目数量的难度等级划分

2.构建支持向量分类模型

支持向量机进行分类首先需要输入训练样本，让分类器学习数据的特征、模式，进而找到分类函数，建立分类模型。本研究将210道阅读理解试题的难度与九个影响因素数据分成十份数据集，在训练集上使用十折交叉验证法训练模型。在模型的训练过程中，对其进行交叉验证时采用了四种常用的核函数，即多项式核函数、径向基核函数、线性核函数以及sigmoid核函数。其准确率，即参照核函数所建立起的支持向量分类模型的结果如表4；其中，总体准确率的计算方式是：正确预测的题目数量除以预测集的题目数量，各类别的准确率是该类别上正确预测的题目数量除以预测集中该类别的题目数量，而类别平均准确率是各类别的准确率的平均值。

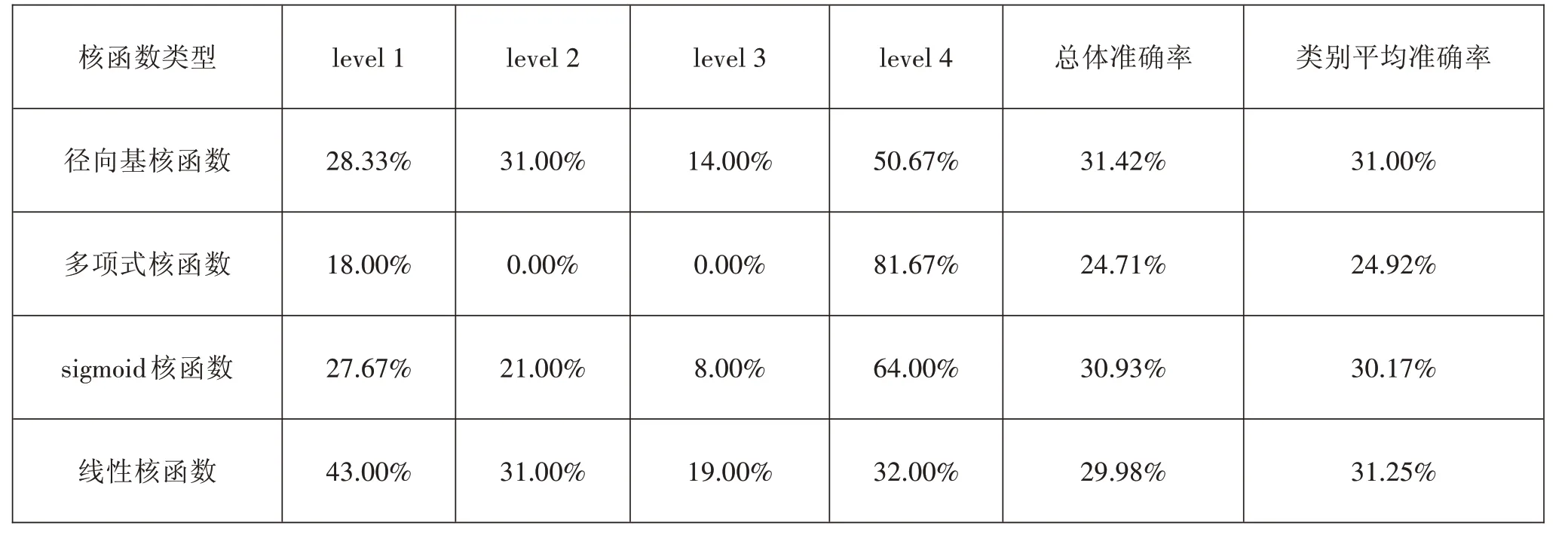
表4四种核函数交叉验证的平均预测准确率

根据表4可以看出径向基核函数的效果最好。总体预测准确率最高的是径向基核函数，其次是sigmoid核函数。类别平均准确率最高的是线性核函数，其次是径向基核函数。基于多项式核函数的分类模型在level2与level3上的准确率为0。sigmoid核函数在总体及各类别上的准确率也较好。

以总体预测准确率最高的径向基核函数建立支持向量分类模型，并采用网格搜索法，在sigma(1,210)及C(2-10,2)的范围内选择出最优sigma参数和惩罚因子的取值，可以参照图1观察参数选择的热力图。图1纵坐标代表的是核参数sigma，横坐标代表的是惩罚因子C。

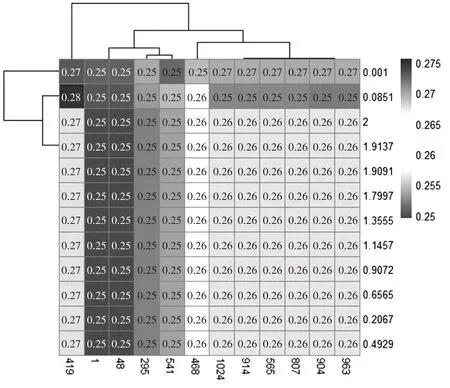
图1径向基核函数的核参数热力图

据图1可知，当C=1.3555，sigma=1时，以径向基核函数构建的支持向量分类模型进行难度预测的错误率最低，为0.25，即此时模型的预测效果最好，预测准确率为75%。

（三）支持向量回归模型的难度值预估

以试题难度作为因变量，以文本题材、文本体裁、文本字数、平均句子长度、文本熟悉词所占比重、选项长度、题目熟悉词比重、干扰项数量以及题目的能力要求等九个变量作为自变量，选择以下四种核函数：多项式核函数、线性核函数、径向基核函数以及sigmoid核函数，对训练集和测试集进行划分时使用十折交叉验证法，进行支持向量回归。四种核函数十次交叉验证的均方误差结果如表5所示。

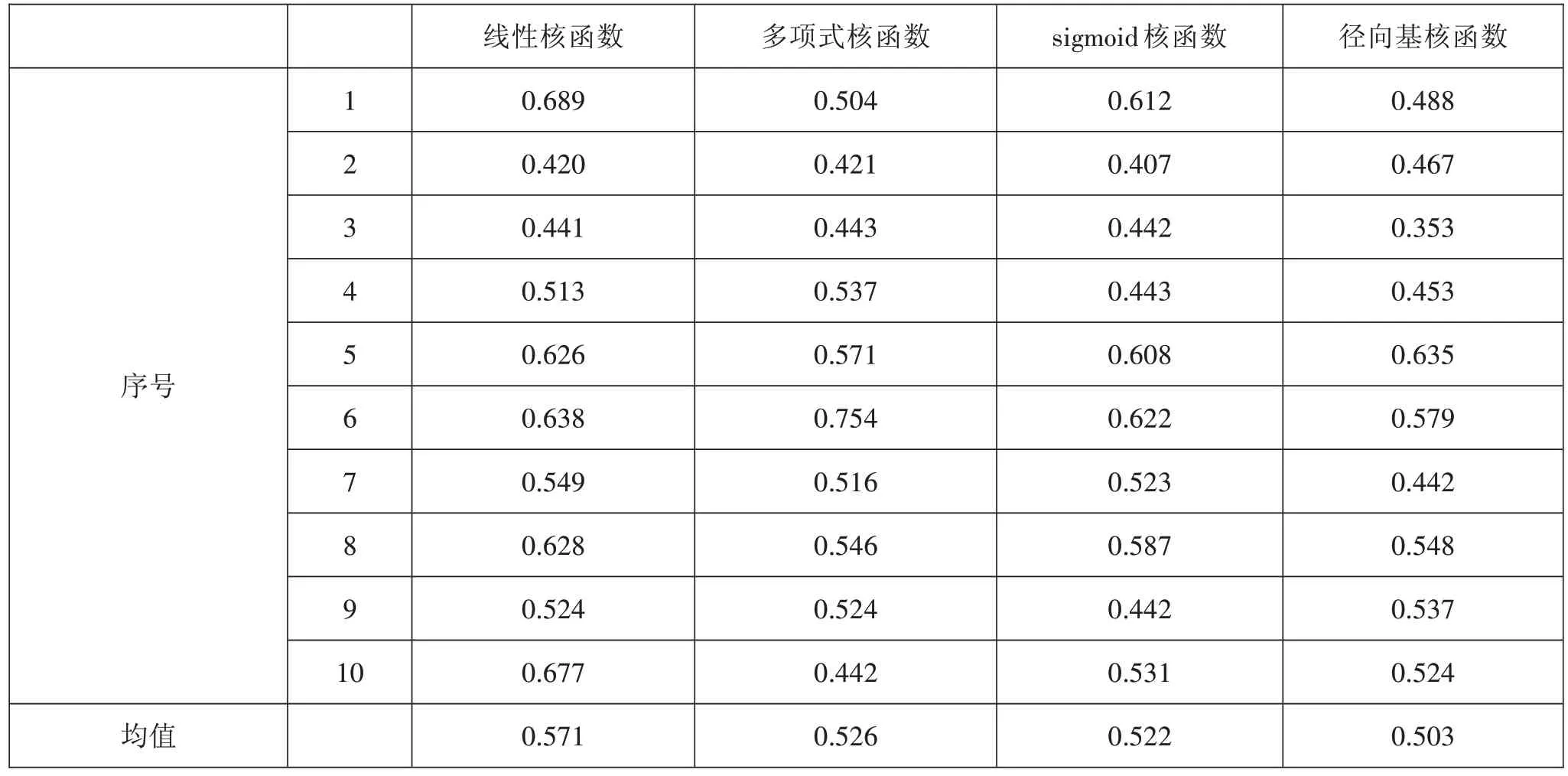
表5十折交叉验证难度预测的均方误差

为了更清晰地显示四种核函数的均方误差差异，将表5中数据以折线图的形式呈现，如图2所示。

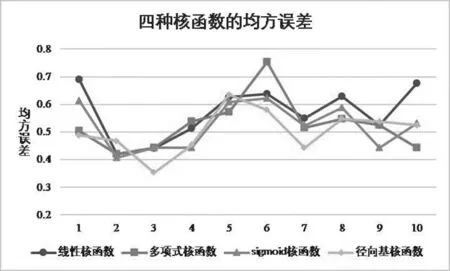
图2四种核函数的均方误差图

根据表图2及表5可以看出，sigmoid核函数的均方误差波动最小，预测效果最稳定。多项式核函数的均方误差波动最大，其均方误差的最大值与最小值相差0.3以上。从十次交叉验证的均方误差均值来看，以径向基核函数构建的支持向量回归模型的平均均方误差最小，其十次结果的平均均方误差为0.503，sigmoid核函数和多项式核函数的平均均方误差也较小，分别为0.522和0.526。

表6是使用径向基核函数进行支持向量回归的一个测试集中试题的预测难度值与实际难度值的对比。

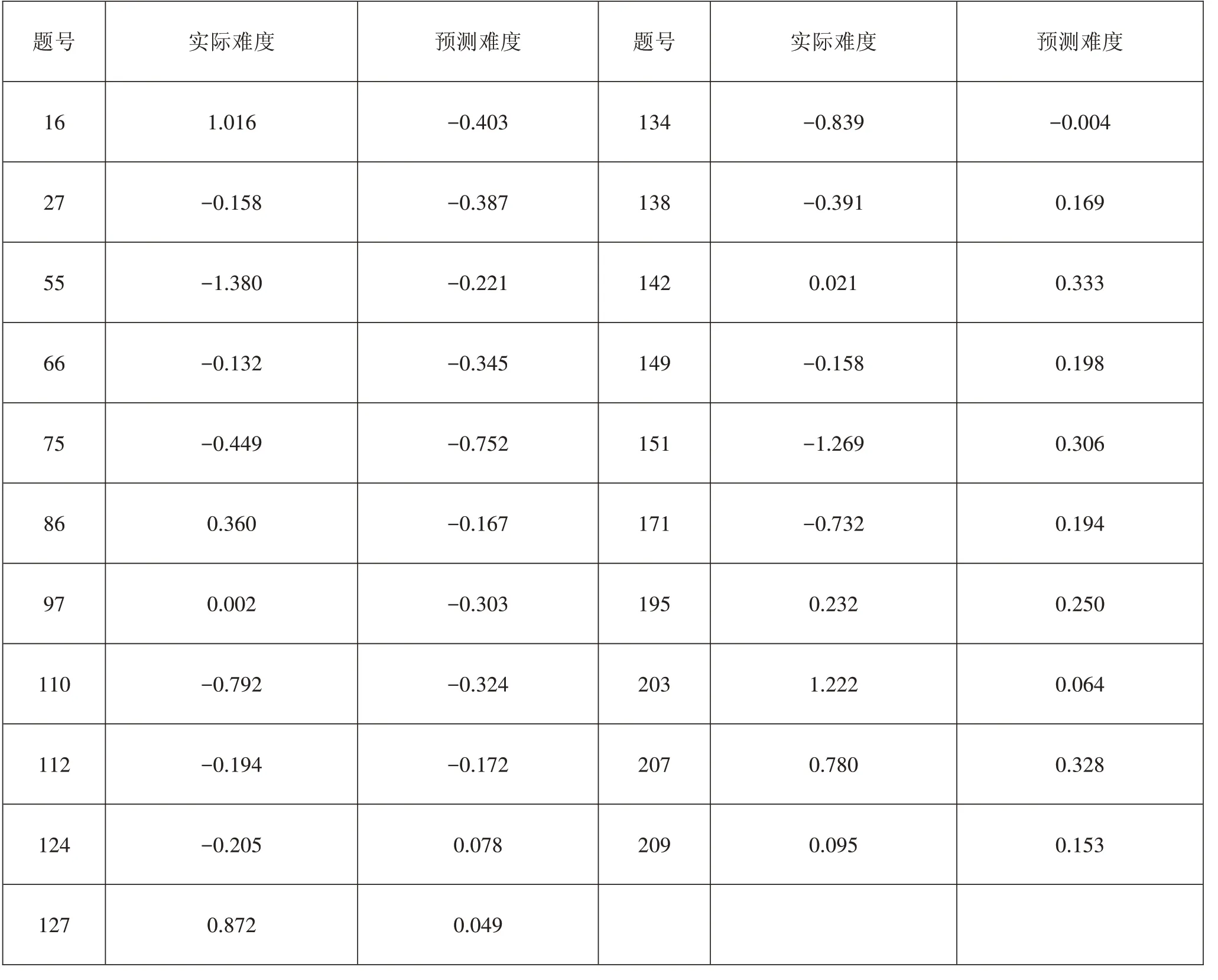
表6径向基核函数的预测难度与实际难度的对比

由于径向基核函数是十个均方误差的均值最小的，因而选择核函数作为支持向量回归模型时，径向基核函数为最优选项，在惩罚因子C∈[0，10]及gamma∈[2-10，2]的范围内经十折交叉验证选出支持向量回归模型的最优核参数，最优模型的核函数及核参数选择如表7所示。

表7最优支持向量回归模型的核函数及核参数

本研究的支持向量回归采用径向基核函数，且核参数取值为C=3.37495及gamma=0.0009765625时模型效果最佳。采用优化后的最佳模型对样本题目数据进行十折交叉验证，得到的十次均方误差及其均值如表8所示。

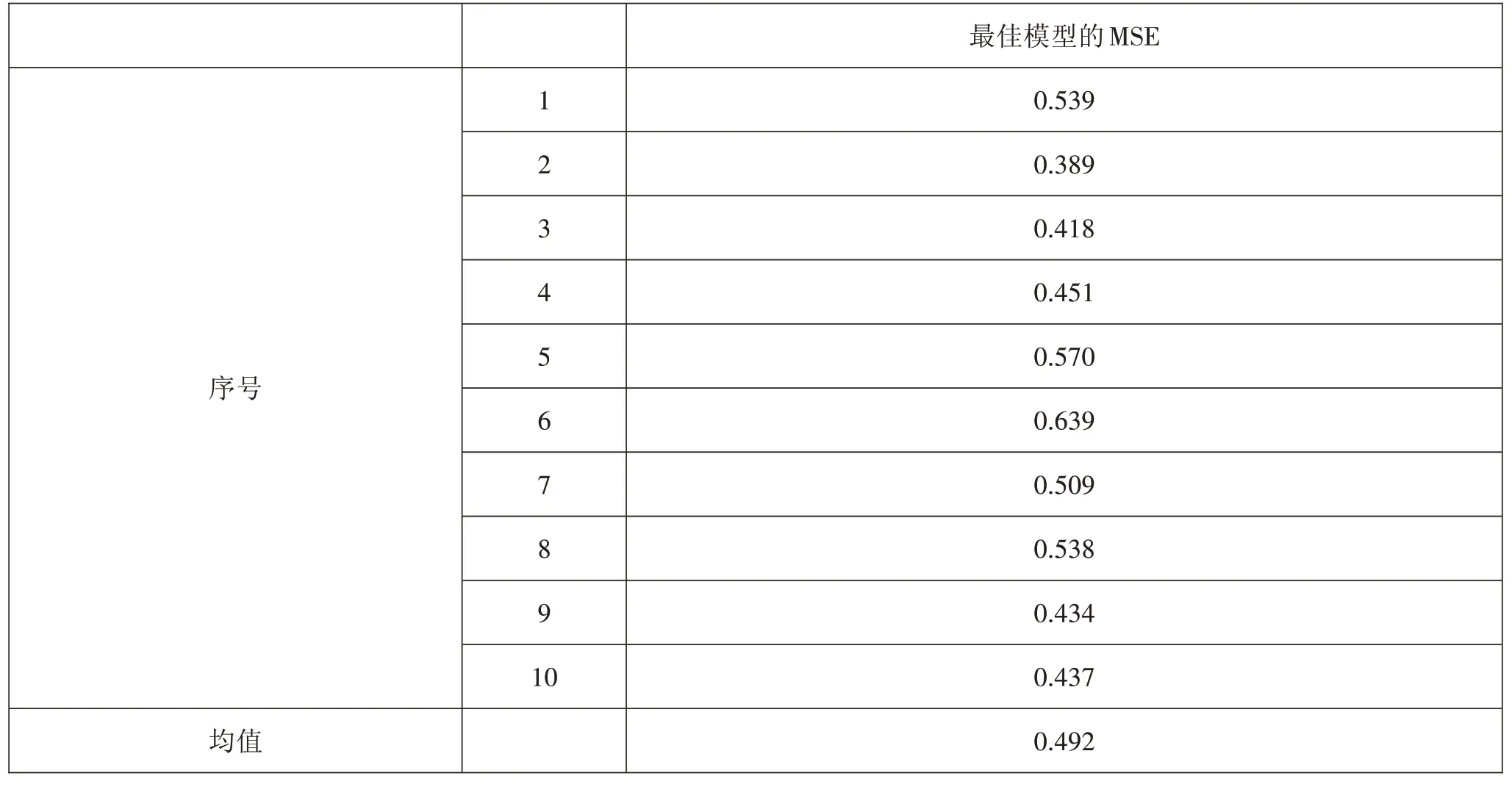
表8最佳支持向量回归模型交叉验证的均方误差

最佳支持向量回归模型进行十折交叉验证的平均均方误差为0.492，比径向基核函数进行核参数优化前的0.503更小。表9是一个测试集中试题的预测难度值与实际难度值。

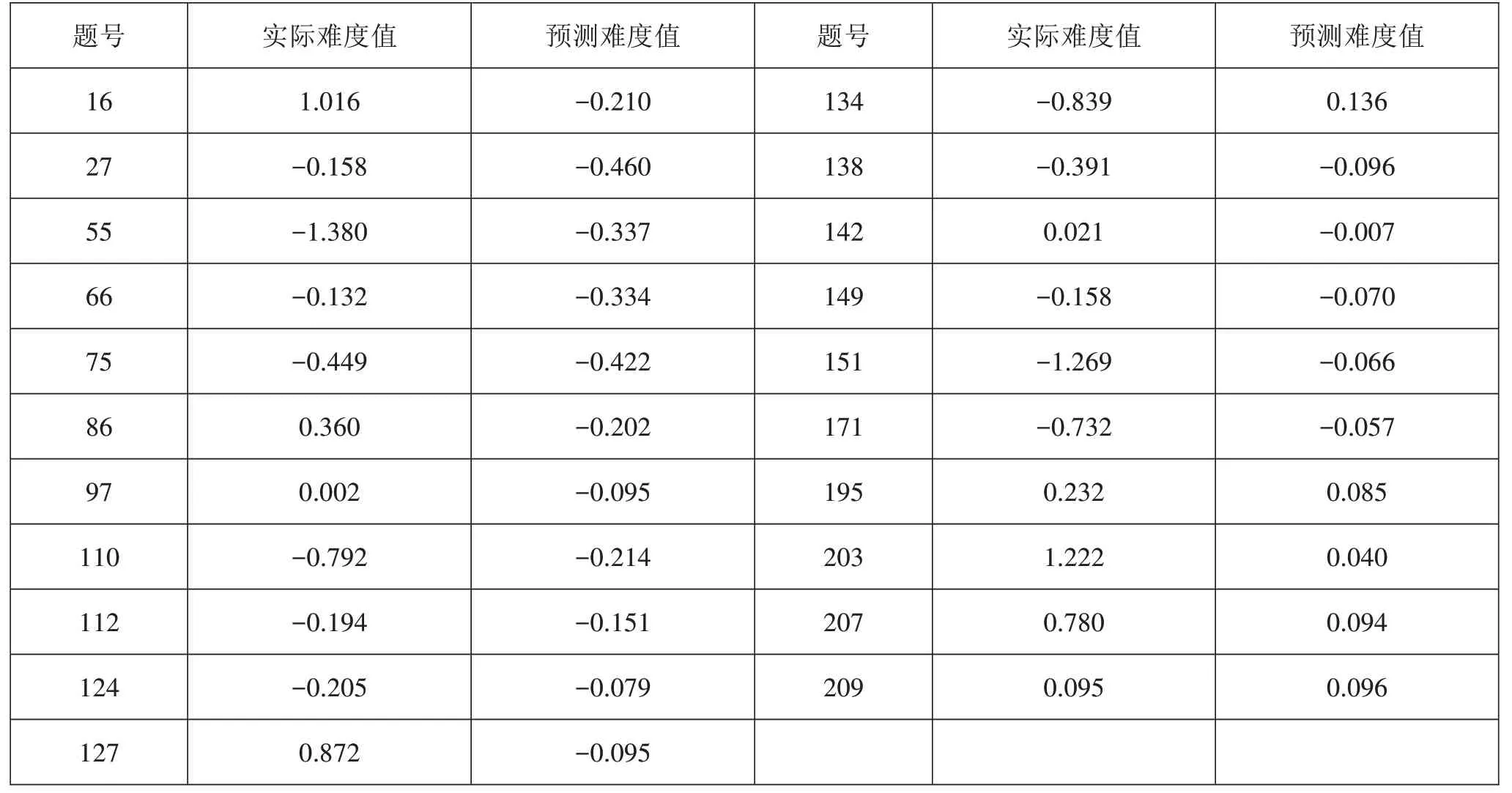
表9最优模型预测难度与实际难度的对比

为了更清楚地呈现模型的预测效果，图3绘制了支持向量回归预测的试题难度与实测的试题难度的折线图。

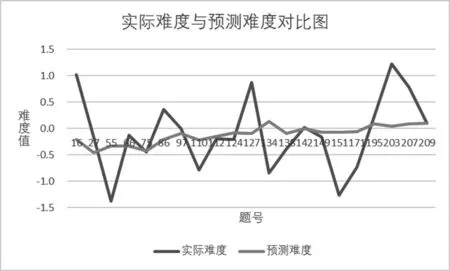
图3实际难度与预测难度对比图

由图3可知，支持向量回归模型对阅读理解试题的难度预测结果与实际难度值差距较大，二者在折线图上的波动趋势并不一致，且模型的预测难度值始终在-0.5至0.3之间，说明支持向量回归模型对阅读理解试题难度值的预测精度不理想。

四、结论与不足

根据计算出来的难度预估效果的评价指标，本研究得出的结论如下：

（一）支持向量机的最优分类模型对难度预估的准确率能够达到75%，支持向量机的最优回归模型的预测难度值与实际难度值的均方误差的平均值为0.492，但其预测的难度值集中在（-0.5，0.2）之间，趋于预测为中间难度。说明支持向量机方法用于阅读理解试题的题目难度预估是可行的，能够对题目的难度类别进行区分，但对于难度值的预测精度不佳。

（二）在使用支持向量机方法构建分类与回归模型时，分别选择了径向基核函数、多项式核函数、sigmoid核函数以及线性核函数四种核函数，其中多项式核函数在两种模型中的表现均不佳，径向基核函数在两种模型中的表现均较好。

在研究过程中，本研究也存在以下不足之处：

在对难度的影响因素进行等级分类时，很难兼顾类别的细致程度与每一类别的样本量，类别划分越精细，每一类别中所包含的样本量必然会减少，导致对这一类别预估的误差变大。本研究将题材按照学科划为了生物、化学、医学、科技等各个小类，因此各类别的样本量较少。

不同的难度影响因素对难度的重要程度是不一样的，明确不同难度影响因素的权重对于提高预估准确率具有重要意义。支持向量机的分类模型与回归模型均能够设置影响因素的权重，但本研究在构建预测模型时未考虑难度影响因素的权重问题，这也是本研究存在的另一不足之处。