基于改进自适应蚁群算法的无人机航迹规划研究

陈 侠， 毛海亮， 刘奎武

(沈阳航空航天大学，沈阳 110000)

0 引言

近年来，无人机技术逐渐成为航空领域最具挑战性和高潜力的技术之一。同时，航迹规划正在成为无人机的关键技术之一，受到世界各国学者的广泛关注。无人机航迹规划的主要任务是在已知起点和终点的情况下，找到一条可以避开障碍的可行路径[1]。

近年来，各国学者提出了许多航迹规划方法，如经典的Dijkstra算法、遗传算法[2]、快速随机搜索树算法[3]、粒子群算法[4]、A*算法[5]、蚁群 (ACO) 算法等。ACO算法自从被意大利学者DORIGO提出后，逐渐被应用于物流、路径规划等领域。该算法是根据蚁群觅食原理设计出的一种群智能算法，具有鲁棒性强、信息反馈好等优点，有利于解决复杂路径规划的问题，被广泛应用于无人机航迹规划[6]。但ACO算法在执行任务过程中存在收敛速度慢、效率低等缺点，于是，有关学者开始对其不断改进来满足无人机的飞行要求。文献[7]利用几何优化方法对蚂蚁进行引导，加快了收敛速度，但存在个别蚂蚁迷失的现象；文献[8]对状态转移函数和信息素更新规则进行改进，加快了算法前期的搜索速度，通过引入信息素调节因子，避免算法后期取得局部最优解，但该算法收敛速度仍然较慢；文献[9]将自适应与ACO算法相结合，提高算法寻找全局最优值的能力，通过自适应并行策略和自适应信息更新策略，提升算法全局搜寻能力，但该算法规划的航迹仍不平滑；文献[10]提出了多启发式改进蚁群 (IACO) 算法，并提出基于路径长度、转弯次数、梯度平滑度3个因素的改进启发式函数，综合计算转移概率，然后根据3个因素综合指标在每个路径上分配信息素量，引导蚂蚁以最佳整体性能接近路径，IACO算法被应用于机器人路径规划。虽然上述文献对ACO算法进行了改进，取得了一些研究成果，但基于改进蚁群的无人机航迹规划算法仍有提升空间，需要提高算法的效率，以满足空战的实际需求。

受到以上研究的启发，本文提出了一种基于改进自适应蚁群(IAACO)算法的无人机航迹规划方法。改进传统ACO算法中的启发式信息、状态转换概率、信息素更新规则，强化了算法的全局搜索能力并加快了收敛速度，提高了无人机的航迹规划效率。仿真表明，本文提出的改进算法可以满足无人机航迹规划中的要求，收敛速度快，能够生成安全、平滑且长度较短的路径。

1 改进的自适应蚁群(IAACO)算法

1.1 ACO算法基本原理

算法的数学表达：在初始时刻，将M只蚂蚁随机置于地图中，并设置所有节点的初始信息素，根据节点的信息素求出蚂蚁从i点到j点的概率，其表达式为

(1)

式中：τi j(t)为当前时刻从i点到j点的信息素浓度；ηi j为与(i，j)相关联的启发式信息；α，β分别为τi j(t)，ηi j的权重参数；N为所有节点数量；T为禁忌表；k表示第k只蚂蚁。

ACO算法迭代过程中信息素浓度值的更新表达式为

τi j(t+1)=(1-ρ)·τi j(t)+Δτi j

(2)

(3)

式中：ρ为信息素挥发系数；Δτi j(t)为当前循环中蚂蚁在t时刻向路径li j释放的信息素；Q为常数；Lk(t)为蚂蚁在本次循环中爬行长度。

1.2 改进的启发式信息

基本ACO算法的启发式信息值与从下一个节点到目标点的距离成反比，从而驱动蚂蚁选择短距离路径。然而，在不考虑当前节点与下一节点位置的情况下，所选路径不一定是最短路径，因此在后期搜索阶段，为了加快收敛速度，启发式信息对路径选择的影响应被削弱。本文引入了自适应调整因子来削弱后期搜索阶段启发式信息ηi j对路径选择的影响，其表达式为

(4)

式中：djG为j点到目标点G的距离；自适应调整因子ε可以表示为

(5)

式中：Nc为当前迭代次数；Nmax为最大迭代次数；e为自然常数。

1.3 改进的状态转移规则

为了提高算法的搜索效率，本节在ACO算法的转移概率中引入角度导向因子，改进的转移概率可以表示为

(6)

式中：μi j(t)为角度导向因子；γ为角度导向因子的权重。μi j(t)可以表示为

μi j(t)=acos θ·χ

(7)

(8)

其中：a为常数；χ为调整因子。

蚂蚁在当前节点位置直线移动到下一行节点与蚂蚁在当前节点位置直线移动到目标点(终点)之间的夹角角度示意图见图1。

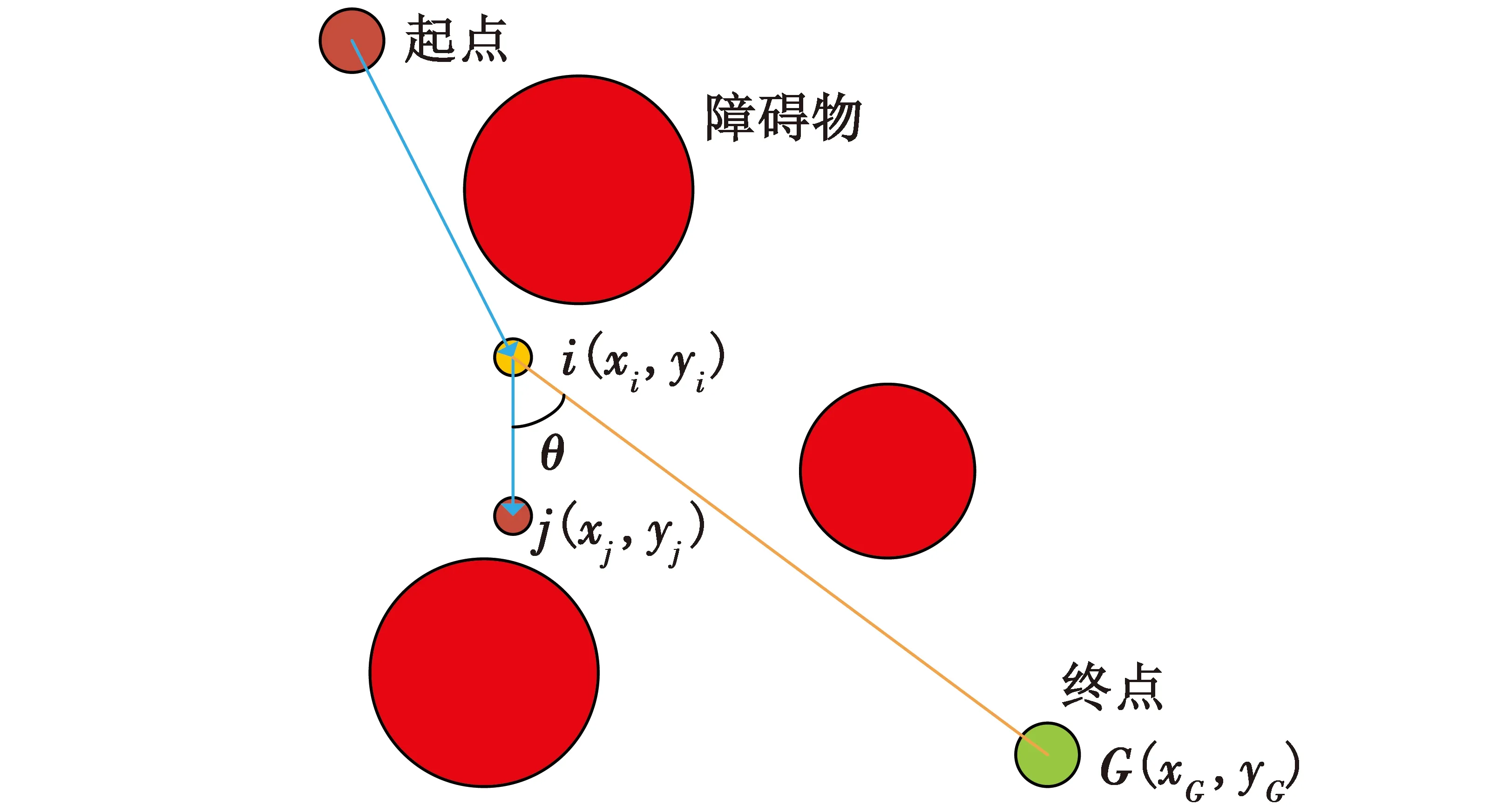
图1 角度示意图Fig.1 Schematic diagram of angle

图1中，i为当前点，j为下一步可行的点，θ为当前点i(xi,yi)至下一可行点j(xj,yj)的连线与当前点i(xi,yi)至目标点G(xG,yG)的连线所成夹角，取值范围为[0°,180°]。根据实际情况，角度θ越小，可行点所在路径越接近于理想路径，此时，角度导向因子μi j(t)越大，蚂蚁选择该路径上的点的概率越大，从而提高了算法的收敛速度。

为了避免蚂蚁在迭代初期盲目搜索，根据参数自适应伪随机比例规则进行状态转移，其表达式为

(9)

式中：q为[0,1]之间的随机数；q0为自适应转换概率的阈值，即

(10)

式中，δ0为比例系数。在迭代初期，q0的值较大，若q≤q0，根据式(6)，蚂蚁会选择转移概率最大的节点，避免了迭代初期盲目搜索；在迭代后期，q0的值较小，若q>q0，根据式(6)，蚂蚁会利用轮盘赌选择下一步要前往的节点，从而提高了全局搜索能力。

1.4 改进的信息素更新规则

为了使蚂蚁的搜索范围集中在最优路径的邻域，在每次迭代后，本文算法只更新到达目标点的蚂蚁走过路径上的信息素，从而避免信息素的盲目更新。

传统的信息素浓度更新公式仅与路径长度有关，本文将目标函数作为信息素更新的变量，改善的信息素浓度更新算式为

τi j(t+1)=(1-ρ)·τi j(t)+ρ·Δτi ji，j∈pbest

(11)

(12)

其中，Jk为蚂蚁k当前迭代路径的性能指标。

在每次迭代后，为了增强最优蚂蚁走过路径的信息素、削弱最差蚂蚁走过路径的信息素，对信息素更新规则进行改进，即

τi j(t+1)=(1-ρ)·τi j(t)+ρ·Q·Jbesti，j∈pbest

(13)

τi j(t+1)=(1-ρ)·τi j(t)-ρ·Q·Jworsti，j∈pworst

(14)

其中：Jbest为当前迭代最优路径性能指标值；Jworst为当前迭代最差路径的性能指标值；pbest为当前迭代的最优路径；pworst为当前迭代的最差路径。

2 目标函数的建立

首先定义了长度指标函数和角度指标函数，然后通过两个指标函数构建航迹优化的目标函数，最后实现了满足无人机航迹规划要求的全局优化。

1) 长度指标函数。

长度指标函数L(p)可以表示为

(15)

(16)

其中:n为无人机经过的路径点总数；pi为路径上的第i个点；(xi,yi)为pi的坐标值；d(pi,pi+1)为从pi到pi+1的欧几里德距离。

2) 角度指标函数。

本文将路径转弯角度作为角度指标的主要影响因素，角度指标函数E(p)可以定义为

(17)

式中：h为无人机的转弯次数；α(li,li+1)为无人机从当前航线进入下一点的转弯角度，其取值范围为[0°,180°]，如图2所示。

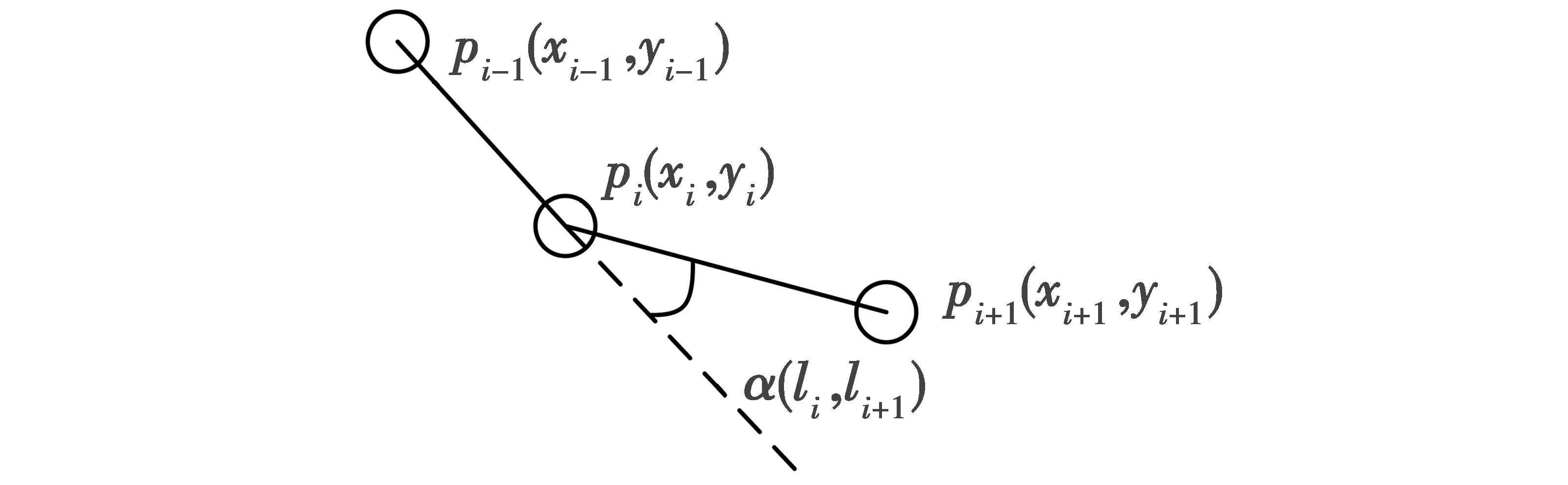
图2 转弯角度示意图Fig.2 Schematic diagram of turning angle

进而，根据长度指标函数和角度指标函数，可以将无人机航迹优化的目标函数J(p)定义为

J(p)=kL·L(p)+kE·E(p)

(18)

式中，kL和kE分别为长度指标和角度指标的权重，且满足kL+kE=1。在算法完成所有迭代后，得到使目标函数J(p)达到最大值maxJ(p)的路径，并将其视为最优路径。

3 算法流程

将本文提出的算法应用于无人机航迹规划问题，其算法流程如下所述。

1) 将二维空间栅格化，得到二维搜索空间的模拟图，可沿X轴将二维空间m等分，沿Y轴将二维空间l等分，所以二维空间可由m×l个栅格来描述，每一个栅格对应一个空间节点。若m=10，l=10，则可将空间划分为100个栅格，如图3所示。

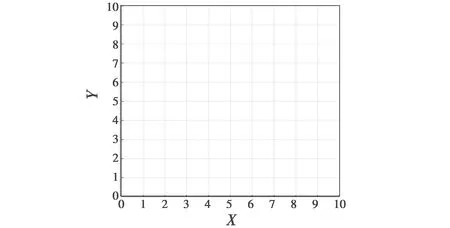
图3 二维搜索空间模型示意图Fig.3 Schematic diagram of 2D searching space model

2) 确定起点、终点、地图障碍信息及算法参数初始化。

3) 将第k只蚂蚁放入初始栅格，k=1,2,…,M。

4) 由式(4)和式(7)分别计算启发式信息及角度信息，蚂蚁根据式(6)和式(9)选择下一步到达的节点，并且将已访问的节点加入禁忌表。

5) 判断蚂蚁k是否到达终点或无节点可选，若是，则进行6)，否则，转到4)。

6) 清空禁忌表，判断蚂蚁数量是否小于数量上限M，若是，则将k加1，转到3)，否则，进行7)。

7) 统计到达目标点的蚂蚁走过路径的长度和角度，根据式(18)建立目标函数，选择最优蚂蚁和最差蚂蚁，并根据式(11)，(13)，(14)更新信息素。

8) 若当前迭代次数小于上限Nmax，将当前迭代次数加1，并转到3)，否则，进行9)。

9) 对航迹进行平滑处理并输出最优路径，算法结束。

4 仿真与结果分析

算法的重要参数如下：最大迭代次数Nmax为30，蚂蚁数量M为8，信息素因子权重α为1，启发值因子权重β为10，角度导向因子权重γ为4，式(7)常数a为2，增强系数Q为1，比例系数δ0为0.5，调整系数κ为0.5，长度指标的权重kL为0.6，角度指标的权重kE为0.4，信息素挥发系数ρ为0.3。

4.1 目标函数优化

在目标函数中，不同权重的取值会导致规划出的航迹不同，为了找到适合的权重，通过分析不同取值下规划出的路径长度和转弯次数来确定权重的取值，如表1所示。

表1 目标函数权重系数优化Table 1 Optimization of objective function weight coefficient

图4所示为不同权重系数下的航迹规划。

当kL=1,kE=0时，得到最短长度的路径，如图4中蓝色带圆圈的虚线所示；当kL=0,kE=1时，得到转弯次数最少的路径，如图4中绿色带*的虚线所示；本文旨在规划出路径更短且转弯次数相对较少的航迹，因此,最终选取kL=0.6，kE=0.4，得到综合最优路径，如图4中红线所示。

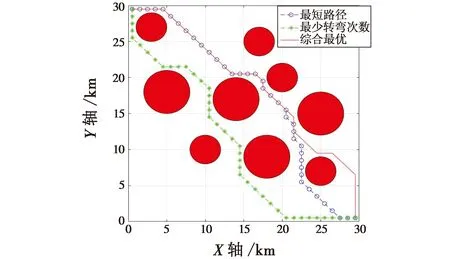
图4 不同权重系数下的航迹规划Fig.4 Track planning with different weight coefficients

4.2 算法的比较分析

为了验证本文提出算法的有效性，在Matlab中分别将ACO算法、文献[10]的IACO算法以及本文IAACO算法应用于无人机航迹规划进行仿真实验。实验环境为简单的9个障碍物环境和复杂的15个障碍物环境。

简单环境可以被划分为30 km×30 km的地图，如图5所示，起点坐标为(1 km,30 km)，终点坐标为(30 km,1 km)。

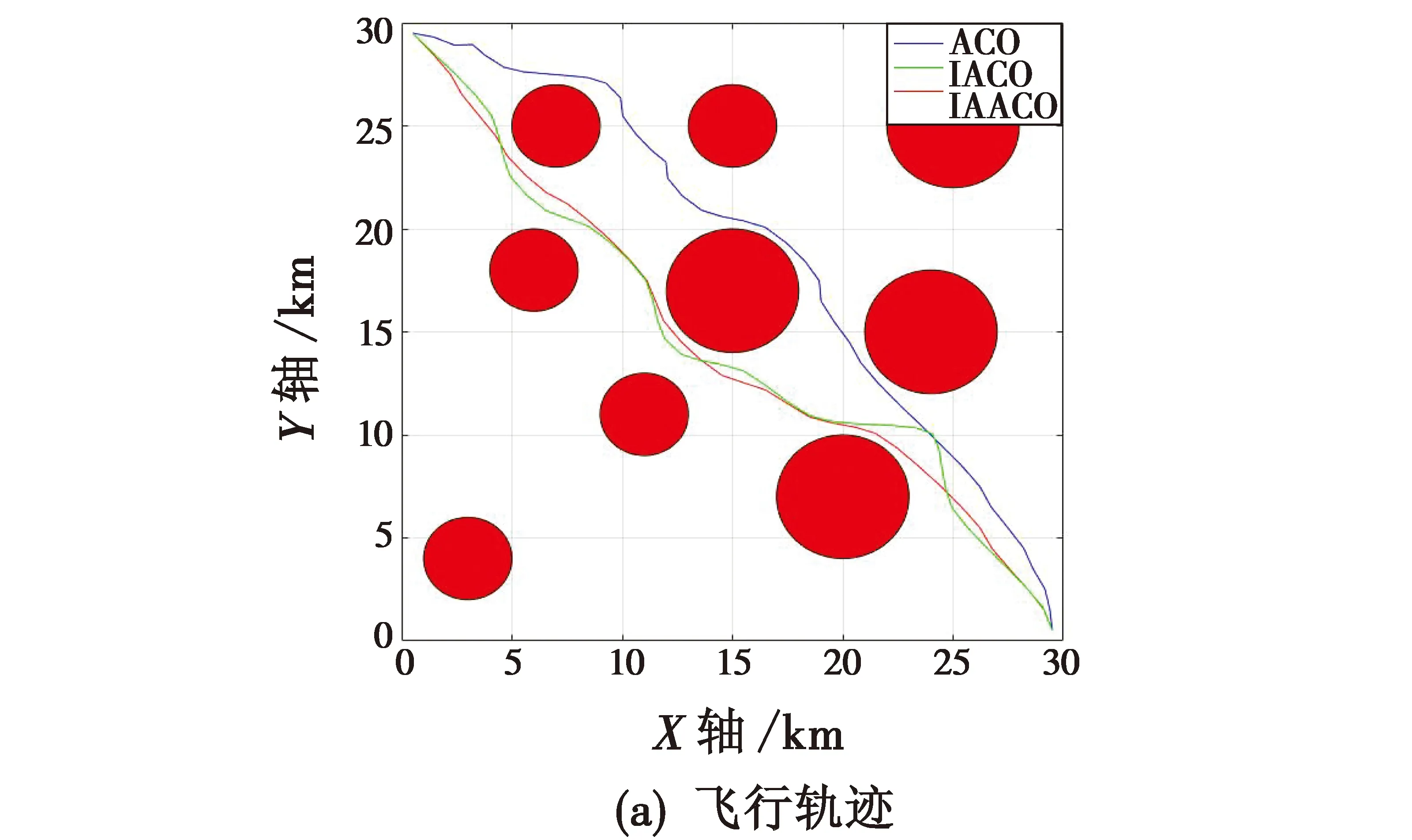
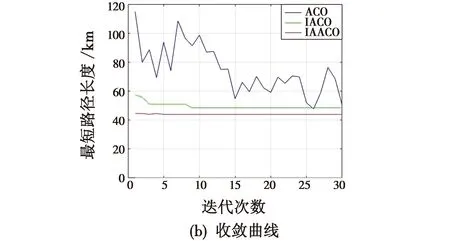
图5 简单环境下仿真Fig.5 Simulation in simple environment

从图5中的飞行轨迹和收敛曲线可以看出，相比于ACO算法和IACO算法，本文提出的IAACO算法收敛速度更快，规划的路径更为平滑且更短。

复杂环境可以被划分为50 km×50 km的地图，相对于简单环境规模更大，且障碍物更多，复杂环境的起点坐标为(1 km,50 km)，终点坐标为(50 km,1 km)。为了验证算法的稳定性，本文在复杂环境中对每种算法分别进行了30次实验，并记录算法的运行时间、生成路径的长度和迭代次数。飞行轨迹与迭代曲线如图6所示，30次实验平均值如表2所示。

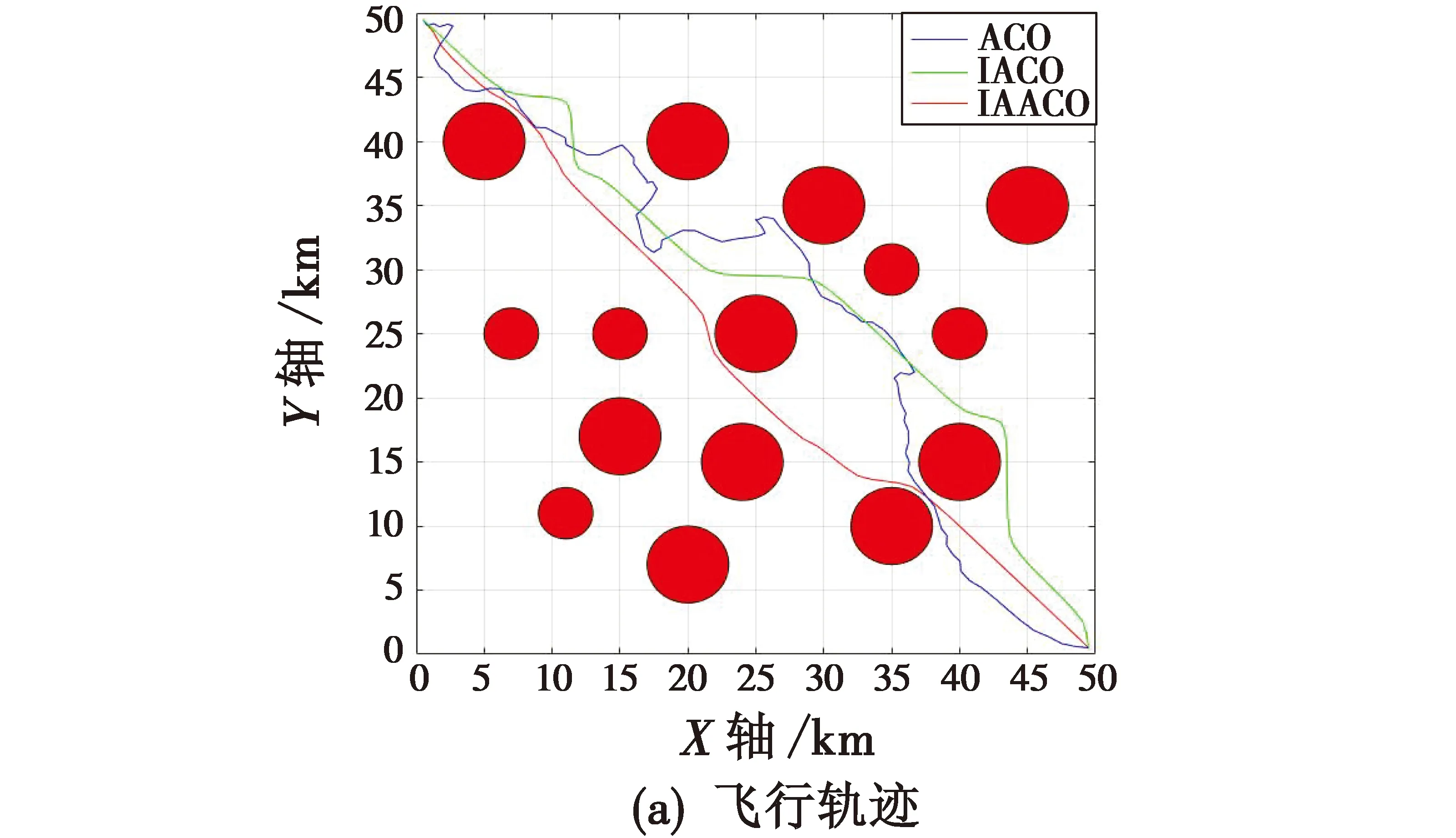
图6 复杂环境下仿真Fig.6 Simulation in complex environment

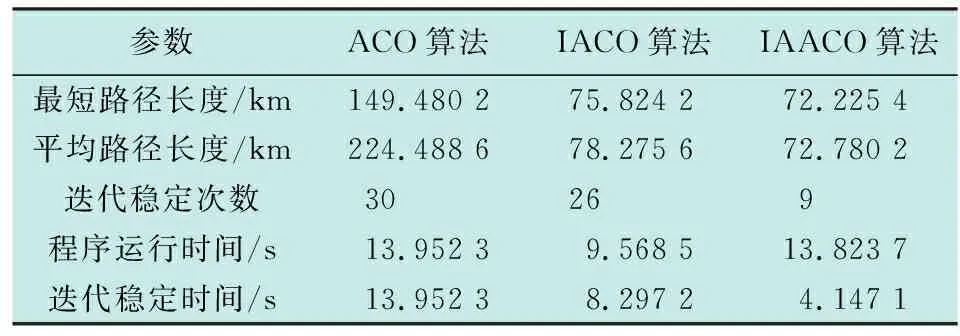
表2 3种算法的30次实验平均值Table 2 Average value of 30 experiments of the three algorithms

结果表明，虽然IAACO算法运行时间相较于IACO算法稍长，但是IAACO算法规划出的路径更短且更加平滑，综合性能表现更好。迭代稳定次数相较于ACO算法和IACO算法更少，因此迭代至稳定的时间更短。

5 结束语

针对蚁群(ACO)算法在无人机航迹规划中存在的收敛速度慢、易陷入局部最优等缺点，本文提出了改进的自适应蚁群(IAACO)算法。通过对二维空间进行网格划分，成功地将本文算法应用于无人机航迹规划问题的求解。实验结果表明，所提算法收敛速度较快，不仅可以安全避开威胁，且规划出的航迹相对平滑、长度较短。但本文只考虑单机航迹寻优，该方法还可以扩展到多无人机的航迹规划中，这有待进一步研究。