公轨合建盾构隧道管片-内部结构复合体系横向抗震性能研究——以济南黄河隧道为例

何应道， 肖明清， 封 坤， 曹翔鹏， 郭文琦

(1. 中铁第四勘察设计院集团有限公司， 湖北 武汉 430063； 2. 水下隧道技术湖北省工程实验室，湖北 武汉 430063； 3. 西南交通大学 交通隧道工程教育部重点实验室， 四川 成都 610031)

0 引言

盾构法以其对地层条件的适应性强、对周边建筑物影响小以及施工安全高效等优点成为目前修建穿江越海隧道的主流工法[1]。随着应用领域的拓展以及盾构技术的进步，大直径成为目前盾构隧道的一个显著特点。为实现土地资源的集约化和隧道断面的最大化利用，越来越多大直径隧道被设计为双层隧道或公轨合建隧道。随着隧道断面增大，隧道内部结构也变得复杂多样。内部结构通常由梁、板、柱等构件组成[2]，其空间布置对于隧道结构的抗震性能可能会产生影响，因此，探明盾构隧道管片-内部结构复合体系的横向抗震性能对保证隧道的正常运营具有重要意义。

目前，已有学者对盾构隧道抗震性能开展了大量研究。在数值模拟方面，刘晶波等[3]基于横断面反应位移法，提出一种非一致地震动下隧道纵向反应分析方法；宾佳等[4]在Pushover方法的基础上，采用自编程序对双线盾构隧道进行拟静力弹塑性抗震研究；张稳军等[5]通过建立三维精细化地层-结构模型，讨论不同地震强度下隧道接缝力学性能和防水性能退化规律；耿萍等[6]针对盾构隧道纵向接头，从整环管片与细部接头2个方面分别分析纵向接头在地震荷载作用下的力学性能；王程等[7]建立管片-内部结构静动力耦合三维有限元模型，分析复合结构在不同震级、不同管片拼装方式下的隧道应力和变形规律。在模型试验方面，张景等[8]以纵向等效刚度模型为基础，开展振动台模型试验，揭示盾构隧道在软硬突变地层条件下的地震响应特性；陶连金等[9]通过振动台试验，研究不同仰坡参数对隧道洞口段抗震性能的影响；信春雷等[10]为研究隧道洞身段抗减震措施，对设置减震缝、减震板的隧道分别开展模型试验，探明隧道在不同抗减震措施下的地震响应规律。

同时，也有部分学者开展了内部结构对隧道力学性能的影响研究。例如： Zhang等[11]开展双层车道公路隧道大型振动台试验，对比内部结构对盾构隧道的抗震性能影响，结果表明，考虑内部结构会抑制隧道断面变形，增加隧道外侧动土压力；黎晨等[12]针对内部结构采用预制双层车道板的盾构隧道，研究了行车荷载下结构的内力分布，并提出一种全新的内部结构设计方法；温竹茵等[13]通过建立二维数值模型，研究预制车道板与管片在铰接、链杆连接、固结和无连接4种接触属性下的力学性能差异；禹海涛等[14]采用梁-实体模型，探究内部结构采用预制与现浇方式时对隧道抗震性能的影响，并给出了内部结构与管片最佳刚度比；吴斌暄[15]建立二维“板-梁-柱”结构体系，比较复合体系在水土荷载下不同接触属性的优劣，结果表明，链杆连接可以同时满足荷载与变形要求；潘文韬等[16]比较了不同内部结构施工方式对隧道抵抗列车长期振动性能的影响，指出全装配内部结构在施工速度和受力变形方面均有较大优势。

通过现有研究可以发现： 1)目前对盾构隧道管片-内部结构复合体系力学性能的研究大多仍集中在行车荷载和水土荷载，而关于地震作用下管片-内部结构复合体系抗震性能的研究鲜有报道。2)内部结构与管片的连接方式通常采取简化处理，对于二维模型，通常将内部结构视作梁单元，与管片接触属性采用铰接、链接和固结，与工程实际不符；对于三维模型，内部结构与管片接触属性通常采用绑定接触，没有考虑到接触面的损伤退化。

鉴于此，本文以济南黄河隧道为工程背景，建立三维有限元计算模型，研究有无内部结构、内部结构不同施作方式对隧道结构横向抗震性能的影响。

1 依托工程概况

济南黄河隧道位于济南市中部，是国内第1条穿越黄河的大型交通隧道。隧道总长度为3 850 m，其中，盾构段长度约为2 519 m。隧址区地貌形态为冲积平原，地势较为平坦。隧道纵断面如图1所示。

图1 济南黄河隧道纵断面图Fig. 1 Profile of Yellow river tunnel in Jinan, China

本隧道为公轨合建隧道，上层为市政道路行车层，布置3条车道；下层布置地铁区间。隧道横断面包括管片衬砌和内部结构2个部分，隧道横断面示意如图2所示。

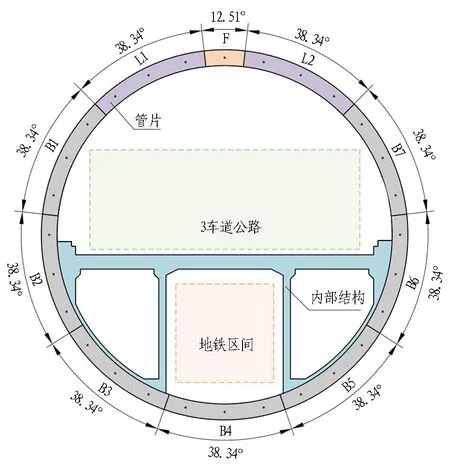
图2 隧道横断面示意图Fig. 2 Schematic of tunnel cross-section

2 数值计算模型

济南黄河盾构隧道主体由预制管片、纵向和横向螺栓拼接而成，内部结构由箱涵、弧形内衬和车道板组合而成。本文拟探究不考虑内部结构以及内部结构不同施作方式下隧道管片-内部结构复合体系横向抗震性能的差异，对模型做如下简化：

1)隧道采用分块处理，每环管片由封顶块、邻接块与标准块拼接而成，纵向与横向螺栓均采用Beam单元模拟(螺栓长度为684.9 mm，直径为36 mm，与接缝面夹角为60°)，管片钢筋网采用Truss单元模拟，考虑了主筋与箍筋对结构的影响。

2)内部结构预制箱涵采用分块处理，箱涵之间采用螺栓连接，非封闭二次衬砌与车道板简化为一个整体，不考虑变形缝的影响。

3)预制箱涵与非封闭二次衬砌内部钢筋网采用Rebar单元模拟，考虑了主筋与箍筋对结构的影响。

2.1 建立计算模型

隧道衬砌结构采用单层装配式钢筋混凝土通用管片环，管片外径15.2 m，内径13.9 m，幅宽2 m，厚0.65 m。模型三维尺寸为180 m×100 m×40 m，隧道埋深26.4 m。计算模型示意如图3所示。

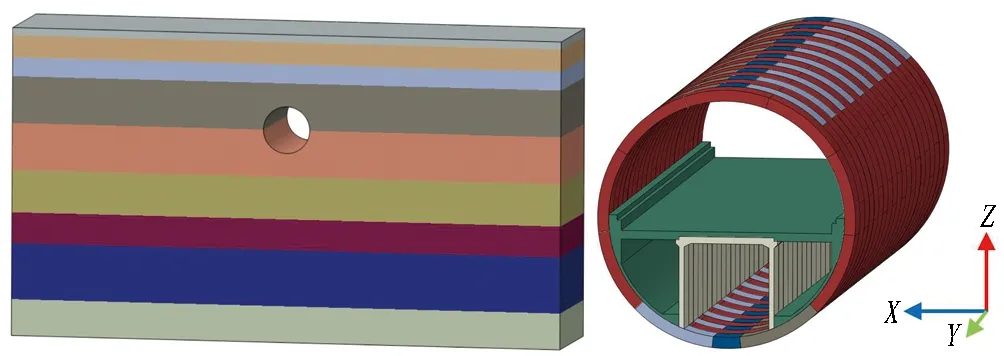
(a) 土体整体模型 (b) 隧道整体模型

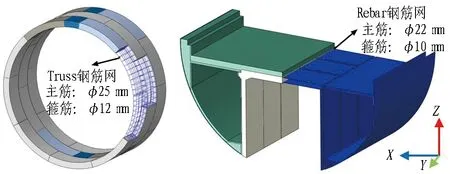
(c) 管片及配筋示意图 (d) 内部结构及配筋示意图 图3 计算模型示意图Fig. 3 Schematic of calculation model

2.2 材料参数

本计算中土层本构关系选用ABAQUS等效线性黏弹性本构[17]，以此模拟土体在地震作用下的非线性特性。土层材料参数取自济南黄河隧道项目最不利钻孔位置的土层参数，各土层动剪切模量比G/Gmax、阻尼比随剪应变的变化曲线如图4所示。

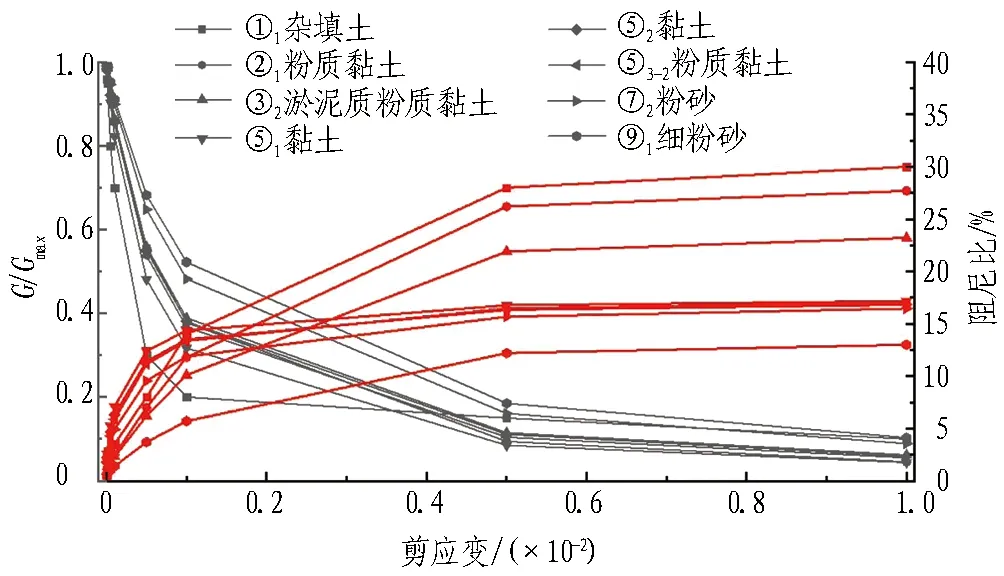
红色线代表阻尼比，黑色线代表动剪切模量比。图4 各土层动剪切模量比和阻尼比随剪应变的变化曲线Fig. 4 Variation curves of shear modulus ratio and damping ratio with shear strain of each stratum

依据《混凝土结构设计规范》[18]中对混凝土本构关系的相关描述，对管片与内部结构引入混凝土损伤塑性本构，以刚度折减系数(SDEG)衡量整体结构抗震性能的优劣[19]。该系数同时考虑单元历史最大受拉与受压损伤，取值为单元折减后强度与初始强度的比值，当参数为1时代表结构完全破坏。图5示出C60混凝土损伤塑性本构。

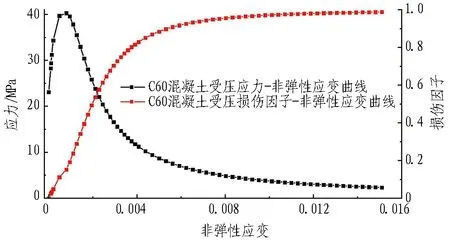
(a) 混凝土受压应力/损伤因子-非弹性应变曲线

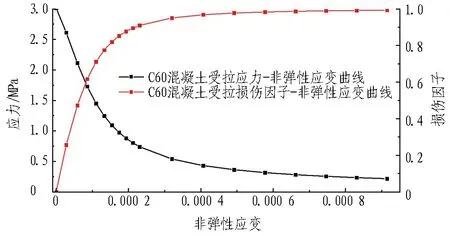
(b) 混凝土受拉应力/损伤因子-非弹性应变曲线图5 C60混凝土损伤塑性本构Fig. 5 Damage plasticity of C60 concrete

管片混凝土强度等级为C60，内部结构混凝土强度等级为C40，均采用混凝土损伤塑性本构，混凝土材料瑞利阻尼系数α与β分别取0.132 3和0.009 7。隧道环向与纵向、预制箱涵之间均采用10.9级高强度螺栓连接。管片与内部结构钢筋网均为HRB400螺纹钢，采用双折线本构。土层力学参数及隧道材料力学参数分别见表1和表2。

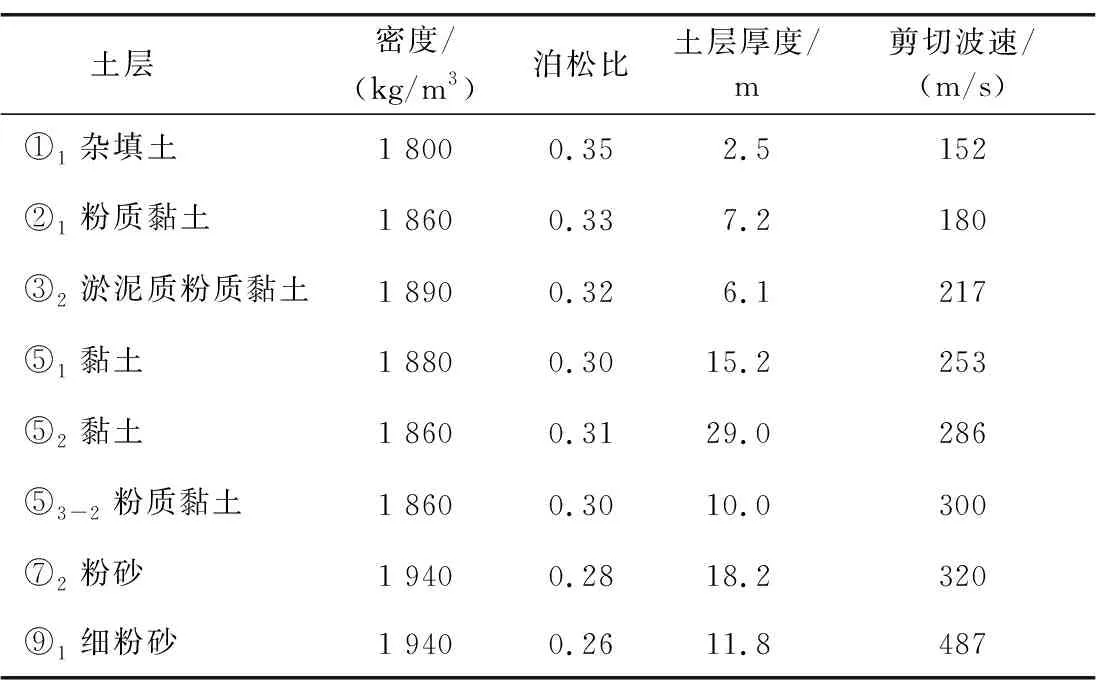
表1 土层力学参数表Table 1 Mechanical parameters of soils

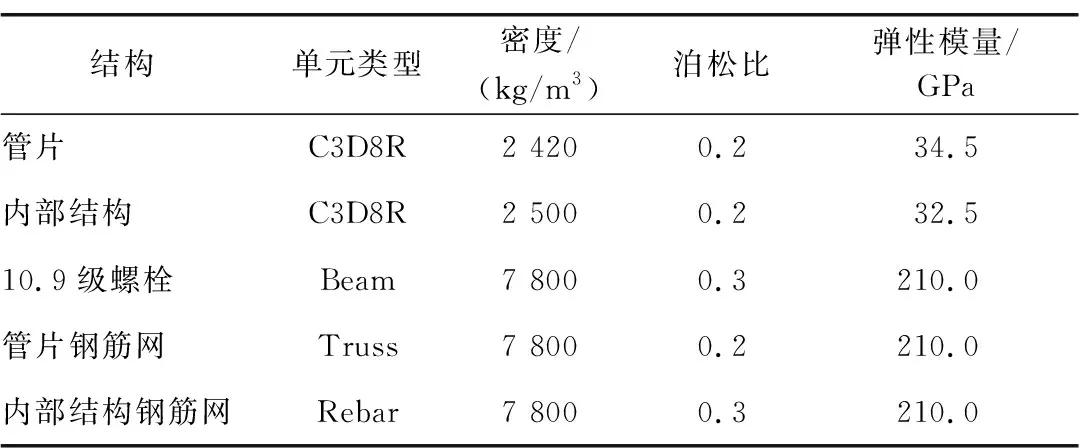
表2 隧道材料力学参数表Table 2 Mechanical parameters of tunnel materials

2.3 荷载输入

根据济南黄河隧道场地地震安全性评价报告可知，该地区地震峰值加速度为0.2g，特征周期为0.45 s，地震持续时间为30 s。本次计算分别输入人工波、Kobe波与El-Centro波，以避免地震动频谱特性对计算结果的影响。3种地震动加速度时程曲线和地震动反应谱曲线见图6。地震荷载采用等效节点力输入，地震动输入方向为X方向，动力边界采用黏弹性人工边界，在ABAQUS软件中采用连接器单元实现黏弹性人工边界弹簧阻尼器的功能。黏弹性人工边界与等效节点力参考文献[20]。

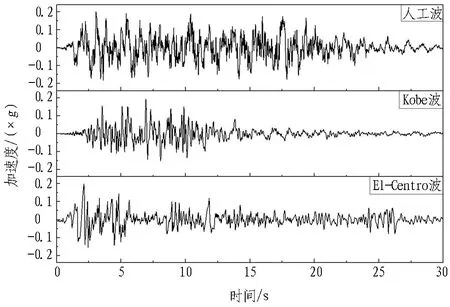
(a) 地震动加速度时程曲线

(b) 地震动反应谱曲线图6 3种地震动加速度时程曲线和地震动反应谱曲线Fig. 6 Time-history curves of three kinds of ground motion acceleration and curves of ground motion response spectrum

本次计算采用静力-动力耦合分析[21]，同时考虑了隧道衬砌和内部结构施工工序的影响，具体计算流程为：

1)土体贯通开挖同时施作管片，采用ODB循环迭代法进行第1次地应力平衡，最大位移达到10-4m时停止迭代。

2)施作内部结构，进行第2次地应力平衡，最大位移达到10-4m时停止迭代。

3)提取静力分析下土体边界处的边界反力，以集中力的形式施加在动力分析模型上。

4)提取静力平衡应力场，将该应力场作为动力分析初始应力场施加在动力分析模型上，完成静力-动力耦合分析。

模型初始应力云图和位移云图见图7。

(a) 静力分析中土体应力云图

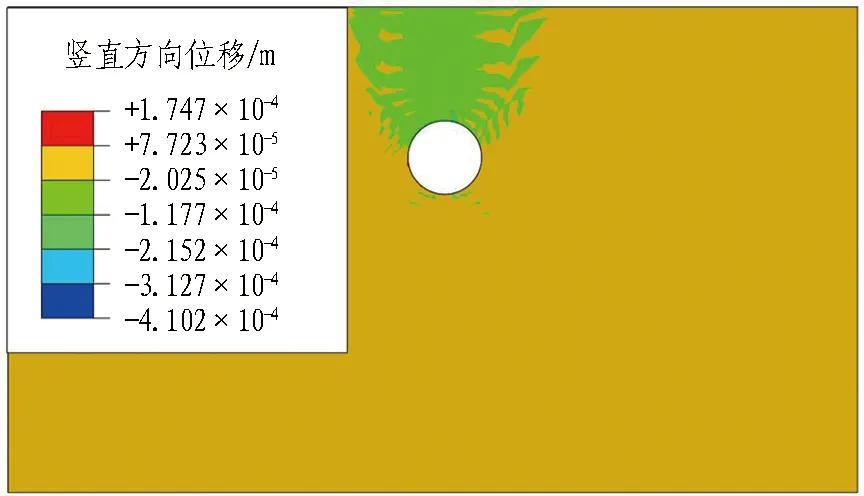
(b) 静力分析中土体位移云图

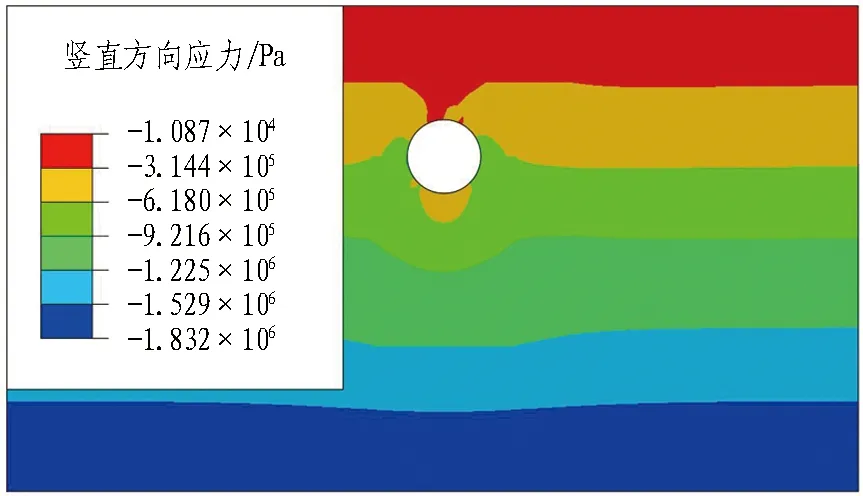
(c) 动力分析中土体应力云图

(d) 动力分析中土体位移云图图7 模型初始应力云图和位移云图Fig. 7 Initial stress and displacement nephograms of model

地震作用下，内部结构与管片、管片与管片、管片与土体之间接触均为高度非线性接触，存在频繁张开错动，应选取合适的接触方式对管片-内部结构复合体系进行动力分析。本次计算中管片表面与土体采用面-面接触，切向摩擦因数取0.4，法向为硬接触；管片与管片、预制箱涵之间采用面-面接触，根据文献[22]，切向摩擦因数取0.5，法向为硬接触。预制箱涵与非封闭内衬采用Tie绑定接触，隧道螺栓、管片钢筋网与内部结构钢筋网均采用Embedded嵌入接触。

2.4 工况设置

本文在对比有无内部结构对隧道横向抗震性能影响的同时，拟对比内部结构施作方式对管片-内部结构复合体系横向抗震性能的影响。内部结构施作方式见图8。

(a) 内部结构全预制(b) 内部结构预制+现浇图8 内部结构施作方式示意图Fig. 8 Schematic of internal structure application method

1)内部结构全预制。对于内部结构与管片，在左右拱腰及拱底位置植入钢筋接驳器，承担部分剪力与弯矩，同时，内部结构与管片接触面采用摩擦接触。

2)内部结构预制+现浇。对于内部结构与管片，在左右拱腰及拱底位置植入钢筋接驳器，同时赋予接触面初始黏聚力。当接触面应力小于黏聚力时，接触面体现绑定接触的性质；当接触面应力大于黏聚力时，则认为接触面开始破坏，黏聚力会随着应变的发展而折减。当黏聚力折减为0时，即从“黏”的状态变为“滑”的状态，此时变为摩擦接触。本次计算中，黏结接触接触面强度取值参考文献[23]中的试验值，文献中为C30混凝土交界面黏结强度，其中，劈拉强度取1.7 MPa，抗剪强度取11.56 MPa。

综上，本次计算采用的3种工况如表3所示。

表3 计算工况表Table 3 Working conditions

3 计算结果分析

3.1 管片及内部结构变形分析

济南黄河隧道内部结构采用公轨合建形式，上层为公路车道，下层为轨道交通，在地震作用下能否降低结构内部变形和提高行车安全是抗震分析的重点。取盾构隧道沿长度方向正中位置的1环管片作为研究对象，提取该环管片拱顶-拱底、左拱腰-右拱腰径向收敛时程曲线,结果见图9。

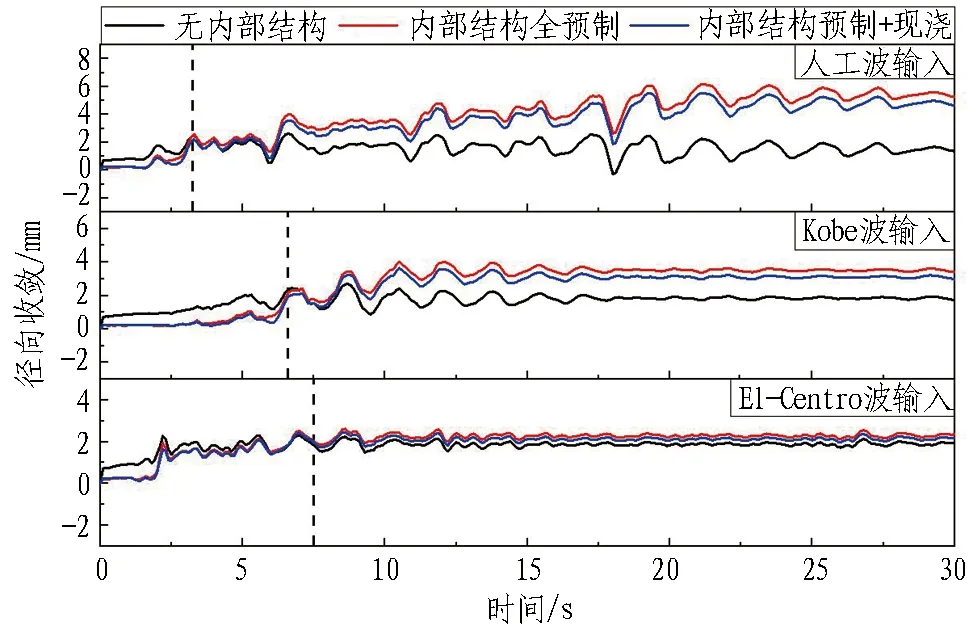
(a) 拱顶-拱底径向收敛时程曲线

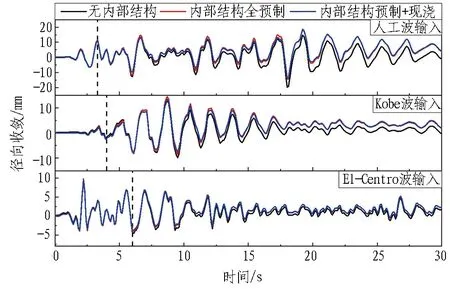
(b) 左拱腰-右拱腰径向收敛时程曲线图9 管片径向收敛时程曲线Fig. 9 Time-history curves of segment radial convergence

观察管片拱顶-拱底以及左拱腰-右拱腰的径向收敛可以发现，基岩地震动特性对盾构隧道变形的影响显著，其中，采用人工波输入时管片变形最大。观察不同工况下管片径向变形随时间的变化，可将管片的变形分为2个阶段：

1)弹性工作阶段，即图9中虚线之前的阶段。此时内部结构并未发生塑性损伤。工况2、3相比于工况1，拱顶-拱底径向收敛最大降低86.87%，左拱腰-右拱腰径向收敛最大降低15.56%，这与文献[11]中的振动台试验结果一致,即内部结构在弹性工作状态时，能够有效控制隧道衬砌的横断面变形。

2)塑性工作阶段，即图9中虚线之后的阶段。随着输入地震动加速度的提升，隧道发生不可恢复的形变，内部结构对管片的约束能力降低。在30 s地震动结束时刻，工况2、3相较于工况1，拱顶-拱底残余变形最大提升74.19%，左拱腰-右拱腰残余变形最大提升126.12%。

比较内部结构与管片不同连接形式下管片的径向收敛，符合“内部结构与管片的连接刚度越大，径向相对位移越小”的规律，这与文献[13]结论相同。在地震动结束时刻，工况3相较于工况2，拱顶-拱底径向残余变形降低15.95%，左拱腰-右拱腰径向残余变形降低3.64%。说明内部结构与管片接触面连接刚度越大，隧道下半部分整体性越好，结构整体刚度越大，管片径向收敛变形越小，且对管片拱顶-拱底径向约束更显著。

对比考虑内部结构与不考虑内部结构在地震动结束时(30 s时刻)管片的径向收敛可知： 工况2、3径向收敛均大于工况1，说明在弹性工作阶段，增大内部结构与管片接触面连接刚度能有效约束隧道变形；在进入塑性工作阶段后，内部结构对拱腰处的约束能力降低，同时由于惯性力和重力等因素的影响，反而会加剧隧道变形。

3.2 管片及内部结构应力分析

3.2.1 峰值应力结果分析

为减小边界效应对应力结果的影响，选取模型纵向正中心2环长度范围内的管片和内部结构，通过ABAQUS后处理模块，分别提取管片与内部结构在总时程下所承受的历史最大峰值应力。

管片及内部结构峰值应力如表4所示。分析表4可知： 1)考虑内部结构会略微提高管片峰值应力，但提升幅度并不明显； 2)工况2、3相比于工况1，峰值大主应力最大提升2.99%，峰值小主应力最大提升8.71%； 3)3种工况下管片峰值小主应力均小于C60混凝土抗压强度38.5 MPa，管片处于安全工作状态。

表4 管片及内部结构峰值应力表Table 4 Peak stress of segment and internal structure MPa

对比2种考虑内部结构的工况可知： 内部结构在地震荷载下承受较大受拉荷载，各工况峰值大主应力均达到C40混凝土峰值抗拉强度。随着内部结构与管片接触面连接刚度的提升，内部结构采用现浇+预制方式会明显提高内部结构的峰值小主应力，工况3相比于工况2最大增幅达54.77%。

3.2.2 应力分布结果分析

为探究管片-内部结构复合体系在地震作用下的应力分布情况，以人工波计算结果为例，在后处理模块中创建沿管片环向的应力路径，分别提取总时程下中间环管片沿应力路径上的峰值大主应力和峰值小主应力计算结果，绘制隧道管片环向峰值应力包络图，结果如图10所示。

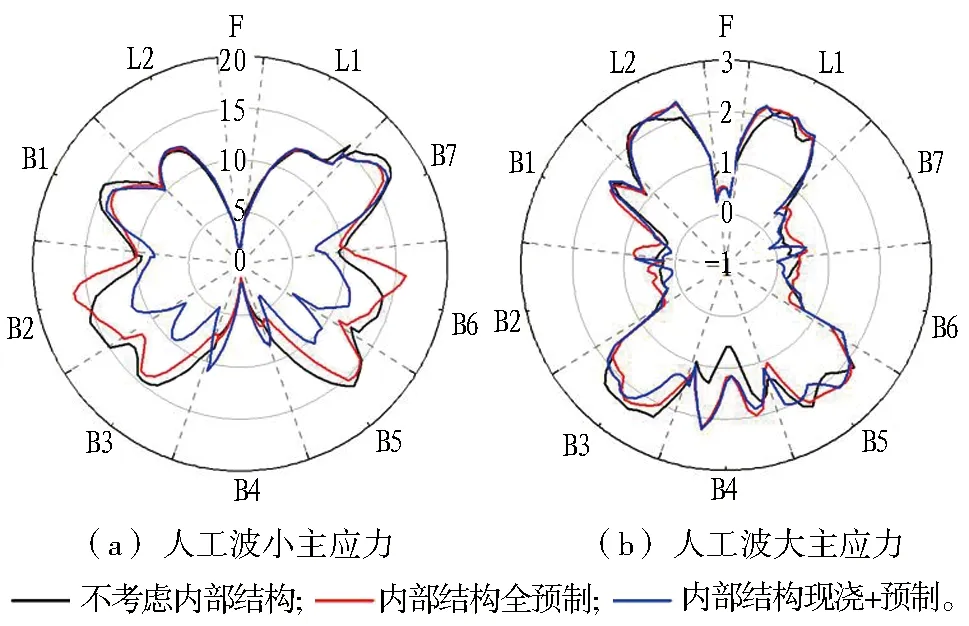
图10 管片环向峰值应力包络图(单位： MPa )Fig. 10 Distribution diagram of segment stress(unit: MPa)

在分布上，由于本次计算采用分块模型，小主应力包络图呈不规则“蝴蝶”形状，大主应力包络图呈不规则“X”形状，横向地震作用下管片在与隧道中线呈45°夹角附近的4个角点上受荷严重。在数值上，考虑内部结构会明显降低内部结构施作区域内管片的峰值应力，随着管片与内部结构接触面连接刚度增大，管片峰值应力降幅明显，应力峰值从大到小依次为： 不考虑内部结构≥内部结构全预制>内部结构预制+现浇。其中，工况3相较于工况1，小主应力最大降低50.75%，大主应力最大降低30.27%。

结合3.2.1节计算结果可知，增大内部结构与管片接触面连接刚度可以充分利用内部结构力学性能，在内部结构施作区域管片与内部结构共同承担地震荷载，可以降低管片局部应力，有利于提高管片-内部结构复合体系横向抗震性能。

3.3 管片及内部结构损伤分析

本节以人工波损伤结果为例，探究管片-内部结构复合体系各工况在地震作用下的混凝土损伤分布以及性能损失。分别提取隧道中间位置管片和内部结构在4.2 s、10.9 s以及18 s 3个人工波加速度峰值时刻的刚度折减系数(SDEG)，绘制刚度折减系数云图，结果如图11所示。

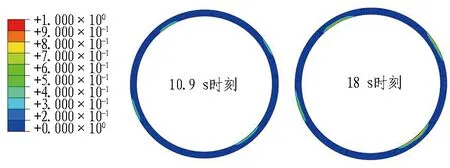
(a) 不考虑内部结构

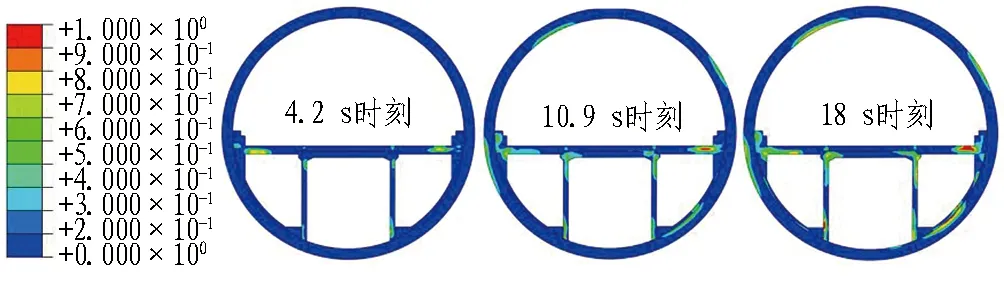
(b) 内部结构全预制

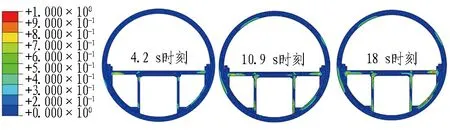
(c) 内部结构现浇+预制图11 管片及内部结构刚度折减系数云图Fig. 11 Stiffness reduction nephograms of segment and internal structure

提取18 s时刻管片与内部结构刚度折减系数最大值作为结构峰值刚度折减系数，提取管片与内部结构损伤单元占结构总单元数的百分比作为结构的损伤占比，结果见表5。

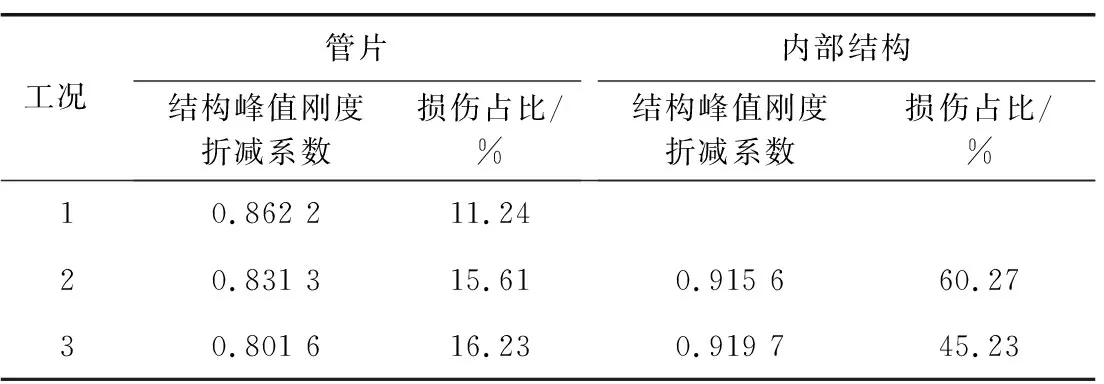
表5 管片与内部结构刚度折减系数及损伤占比表Table 5 Stiffness reduction coefficients of segment and internal structure

分析图11和表5数据可知：

1)在横向地震下，管片竖向45°共轭方向损伤较为严重，主要体现为管片偏压下的受拉破坏。内部结构的损伤发展呈阶段性，最先破坏的位置在车道板与管片连接处、预制箱涵与弧形内衬连接处及车道板与预制箱涵搭接处，内部结构先于隧道发生损伤破坏。

2)随着地震动加速度的增大，各位置刚度折减系数增大，损伤区域进一步扩展。在18 s时刻，内部结构损伤严重区域集中在右拱腰车道板与弧形内衬连接处及弧形内衬与管片右下拱腰连接处，且刚度折减系数均大于0.9，可以认为局部失去承载能力，在设计中需要着重考虑以上部位的加固。

3)对比工况1与工况2、3可知，考虑内部结构会降低管片的峰值损伤，但会增大管片损伤范围，内部结构在分担管片应力与损伤的同时，也会将损伤区域分担到附近管片。随着内部结构与管片接触面连接刚度的增大，刚度折减系数最大降低0.060 6，损伤占比最大增大4.99%。

4)对比工况2和工况3可知，随着内部结构与管片接触面连接刚度增大，内部结构刚度折减系数略微增大，内部结构损伤区域占比明显降低，工况3相较于工况2损伤区域占比降低15.04%。

综上可知，增大内部结构与管片接触面连接刚度可以充分发挥内部结构力学性能，内部结构与管片在地震荷载下能够协调变形，有效抑制车道板、弧形二次衬砌与管片间的张开错动，有利于提升管片-内部结构复合体系的横向抗震性能。

3.4 管片内力分析

为进一步分析不同工况下管片-内部结构复合体系在横向地震作用下的抗震性能差异，本节采用ABAQUS-Python二次开发技术，编制Python程序，并在后处理模块批量提取关键管片环沿环向的84个截面，计算每个截面的峰值弯矩与轴力，得到管片环向的弯矩和轴力包络图，如图12所示。

图12 管片内力包络图Fig. 12 Segment internal force envelope diagram

由图12可知： 由于本次计算采用分块模型，管片弯矩包络图呈现不规则“蝴蝶”状分布，管片轴力包络图呈现不规则“X”状分布，峰值均发生在隧道竖向共轭45°位置。在隧道轴线以上无内部结构区域，3种工况下的弯矩和轴力峰值基本相同；在隧道轴线以下区域，考虑内部结构能明显降低管片弯矩峰值。随着内部结构与管片接触面连接刚度增大，管片与内部结构连接紧密共同受荷，管片内力下降更为显著，这与3.2.2节和3.3节结论一致。其中，工况2、3相较于工况1弯矩分别降低393.2 kN·m(标准块5处)和769 kN·m(标准块3处)，最大轴力分别降低734 kN(标准块5处)和1 798 kN(标准块5处)。

观察3种工况下隧道中线车道板与管片连接处的弯矩值，工况1和工况3隧道中线处的弯矩变化曲线光滑，没有发生弯矩突变；而工况2由于内部结构与管片内壁仅为摩擦接触，两者在地震荷载下频繁张开与互相撞击，管片拱腰位置发生局部的弯矩集中，工况2相较于工况1、3弯矩分别增大613 kN·m和796 kN·m，若采用全预制内部结构，则需要对该位置进行局部补强处理。

4 结论与建议

本文依托济南黄河隧道，通过有限元计算比较有无内部结构、内部结构不同施作方式对管片-内部结构复合体系横向抗震性能的影响，得到如下结论：

1)管片-内部结构复合体系在地震作用下径向收敛呈阶段性变化。在内部结构弹性工作阶段，增大内部结构与管片接触面连接刚度能有效约束隧道变形；在内部结构进入塑性工作阶段后，连接处单元刚度发生折减，对拱腰处约束能力降低，同时，由于惯性力和重力等因素的影响会进一步加剧隧道变形，地震动结束时刻2种有内部结构的工况隧道残余变形均大于无内部结构的工况。

2)考虑内部结构会明显降低内部结构施作区域管片的峰值应力，相对应地，也会降低管片的峰值损伤，小幅度增加损伤区域。其中，管片峰值小主应力降低50.75%，大主应力降低30.27%，管片刚度折减系数降低0.060 6，损伤区域增大4.99%。随着内部结构与管片接触面连接刚度增大，内部结构与管片协调变形能力增强，能够充分发挥内部结构的承载能力，工况3相较于工况2内部结构小主应力提升54.77%，损伤区域占比降低15.04%。

3)内部结构能降低管片局部轴力与弯矩，随着接触面连接刚度增大，左下与右下拱腰处弯矩和轴力均明显呈下降趋势，弯矩最大降低769 kN·m，轴力最大降低1 798 kN。当内部结构采用全预制时，由于内部结构与管片拱腰处约束较弱，部件之间频繁发生张开与撞击，管片拱腰位置会发生弯矩集中现象。

综合来看，对于公轨合建盾构隧道，考虑内部结构能够降低弹性阶段隧道的径向收敛，降低内部结构施作区域内的应力、内力与损伤，有利于提升管片-内部结构复合体系的抗震性能，但应避免内部结构过早进入塑性工作阶段。内部结构的施作方式对管片-内部结构复合体系的横向抗震性能有重要影响，在实际工程中应尽量提高内部结构与管片接触面的连接刚度，提升两者协调变形的能力，充分发挥内部结构的力学性能。