动态约束下可重构模块机器人自适应滑模控制方法
2022-09-19刘先学
刘先学,李 婕
(山东省诸城市机关事务服务中心,山东 诸城 262200)
由于现代机器人自动化程度较高,可在一定程度上代替人力劳动,因此其研发备受关注。经过多年的研究与发展,该项技术已经被应用于工业、航天、娱乐、采矿、探险和医学等多个领域,存在部分功能无法完善的缺点,应用效果有待提升。目前部分机器人受到性能的影响无法应用于特定环境,或无法具有多项功能,随着科技的发展,机器人的能力将不断得到完善,其应用范围也会逐渐扩大。由于目前机器人可实现的功能过于简单,针对复杂任务,通常会采用具备不同特性的机器人来完成,该方法需要增加大量的成本。
目前,模块化设计概念正在电力电子工程、计算机软件工程、机械工程等多个领域中发挥作用,其基本思路是把一个复杂、繁琐的系统切割为具有各种功能的模块,让这些模块处于相互独立的状态,既易于维护,又能更好地保证各模块之间应用逻辑清晰。为提升固定结构机器人的应用性能,部分学者将模块化设计的概念引入机器人设计中,提出了可重构模块机器人的概念。为研究多自由度串联机器人的动力学模型,郑银湖等[1]提出基于双曲正切函数的工业机器人滑模控制方法。该方法主要是将机器人的滑模控制算法与双曲正切函数相结合,对其进行优化,从而在保障其原有不变性和抗扰动性的基础上大幅削减其输入信号的抖振,以解决电机冲击力大的问题。该方法在应用的过程中自适应能力一般,且对末端的约束力较差。郭文东等[2]提出基于模糊干扰观测器的自适应滑模跟踪控制方法,基于反演技术设计运动控制器和动力控制器,在运动控制器中采用分流技术克服了轨迹跟踪初期经常存在的速度跳变问题,在动力控制器中将模糊干扰观测器与自适应滑模控制相结合,解决未知扰动对其的影响。该方法在应用过程中自适应能力较好,但跟踪性能较差。针对上述问题,本文提出了动态约束下可重构模块机器人自适应滑模控制方法。
1 基于可重构模块的机器人运动学关系分析
在研究机器人滑模控制前,先根据运动学原理分析机器人各模块间的运动学关系。通过改变模块的装配方式可完成不同机器人的构形。一个n自由度可重构模块机器人的几何构形可用下面三维构形矩阵R描述:
(1)
式中:On代表第n个可重构模块机器人关节模块的输出口类型;L0代表可重构模块机器人第一个关节模块和基座模块的连接方位;Ln代表可重构模块机器人末端工具模块与第n个关节模块的连接方位;I1,I2,I3代表可重构模块机器人关节模块输入口的类型;0元素代表占位符。两个三自由度的可重构模块机器人构形及其构形矩阵如图1所示。
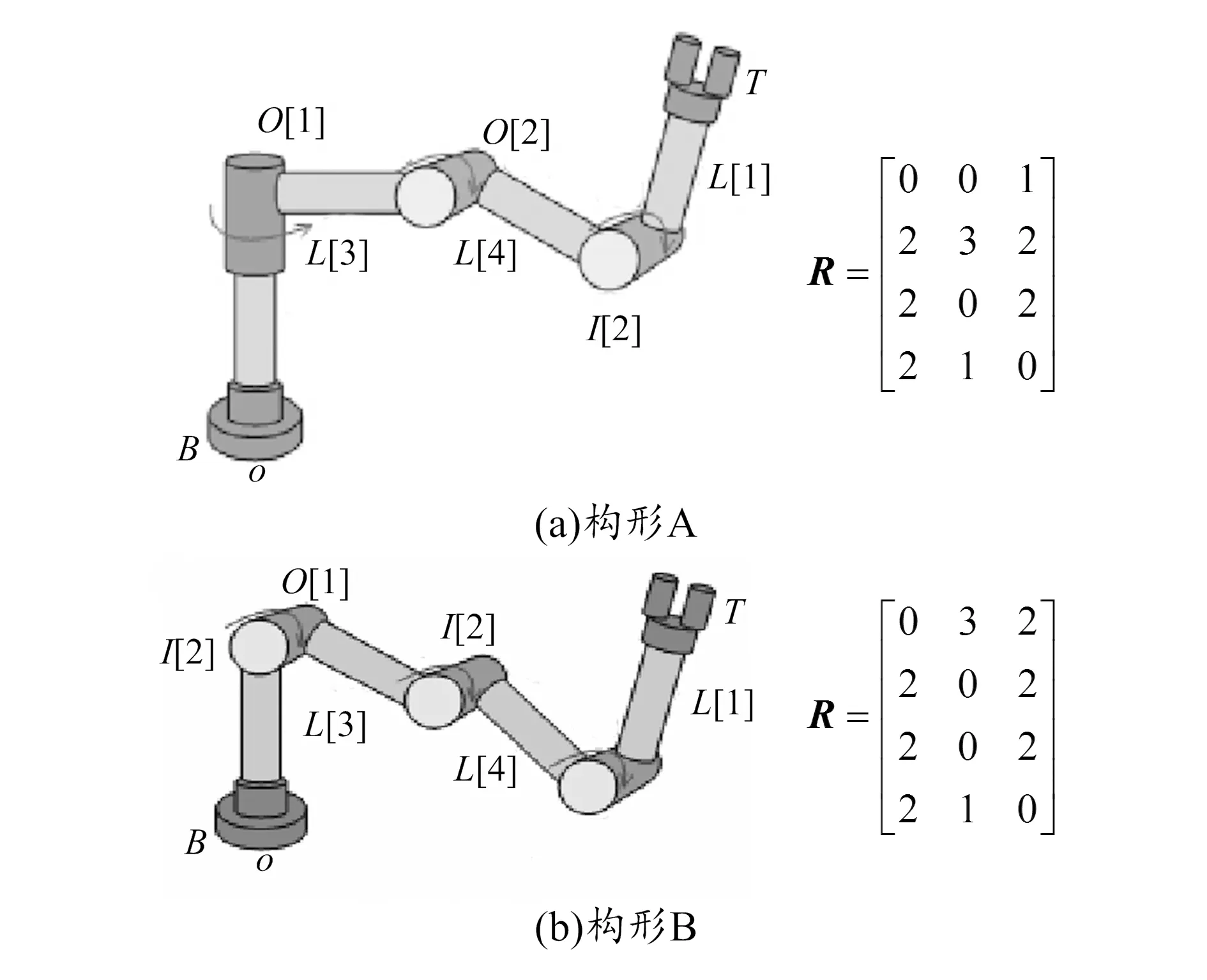
图1 机器人构形及构形矩阵
通过可重构模块机器人的主要架构构建两端坐标系[3]。基座模块与工具模块的特征函数为:
B=Trans(0,0,l)
(2)
T=Trans(0,0,l)
(3)
式中:B为基座模块特征函数;T为工具模块特征函数;Trans(0,0,l)为调用函数,即沿x,y,z轴分别移动0,0,l的距离。
在可重构模块机器人关节模块上建立坐标系。o为模块坐标系,其z轴与关节模块的旋转轴重合,I[1]和I[2]为输入口坐标系,O[1]和O[2]为输出口坐标系[4]。根据牛顿-欧拉迭代方程建立动力学模型,其中一个关节模块的几何参数可用下面4个齐次变换矩阵描述:
JI[1],o(0)=Trans(0,0,d)
(4)
(5)
Jo,O[1](0)=Trans(0,0,d)
(6)
(7)
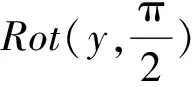
了解每个模块的几何参数以及它们之间的联系后,可得到模块之间的运动学关系。n自由度可重构模块化机器人的运动学关系可表示为:
(8)
(9)
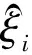
将式(8)、式(9)相乘,得到可重构模块机器人的运动学方程:
T0,n+1(q)=T0,1(q1)T0,2(q2)…T0,n(qn)Tn,n+1
(10)
2 自适应滑模控制方法
得到机器人各模块间运动学方程后,为提高机器人的自适应能力,基于等效控制径向基(RBF)神经网络设计自适应滑模控制方法。选择可重构模块机器人滑模面,对其进行控制,跟踪误差方程s(t)为:

(11)
式中:λ为位姿误差控制系数;ec为可重构模块机器人的位姿跟踪误差;t为时间。选取2个输入、N个隐藏单元及2个输出的网络结构,将RBF神经网络的输入与跟踪误差方程相结合[5],获得的RBF神经网络的输出BNN(i)为:
(12)
式中:Wi为网络向量;Hi为径向向量。RBF神经网络的稳定函数hij表示为
(13)
式中:exp(·)为调动函数;xi为RBF神经网络第i个输入节点函数;cij和σij分别为RBF神经网络第i个输入的第j个节点的中心和底部宽度,均大于0。假设神经网络逼近的最佳值BNN为:
(14)
式中:W1,W2为网络向量;H1,H2为径向向量。则BNN的等效控制变量B1为:
B1=BNN+ε
(15)

(16)

A=βiHiec(i) i=1,2
(17)
式中:βi为学习率;ec(i)为可重构模块机器人的位姿跟踪误差函数。为弥补由于网络不确定性对系统模型的影响,切换控制规则,提出一种基于比例控制的自适应滑模控制方法,以克服网络的初始学习错误,提高系统的暂态响应。
(18)
式中:Bhc为自适应控制权值;kp为比例系数;Bsw为切换的控制系数。Bsw可表示为:
Bsw=Γsgn(s)
(19)
式中:Γ为滑模控制的增益;sgn(s)为阶跃函数。当时间t≥0时,机械手的滑移运动轨迹误差公式如下:
(20)
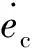
速度跟踪误差公式为:
(21)

此时,神经滑模控制方程B2为:
(22)
在控制过程中,除引入开关控制以消除错误外,还针对抖动,引入RBF神经网络对Γ进行调节。则RBF神经网络的输出Γi为:
(23)
式中:Ai为网络的权向量;ψi为径向基向量[7]。由此,径向基函数的输出φij可用下式表示:
j=1,2,…,m
(24)

(25)
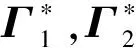
(26)

(27)
式中:κi为学习率;si为速度跟踪误差。由此,可得可重构模块机器人自适应滑模控制方程B3为:
(28)
3 实验结果与分析
为验证所提控制方法的有效性,对具有两个自由度的可重构模块机器人进行实验分析。实验平台为MATLAB,被测试的可重构模块机器人实物图如图2所示,实验参数见表1。

图2 可重构模块机器人

表1 实验参数
选用传统一阶滑模控制方法作为对比方法,与本文所提的控制方法进行对比分析,得到应用两种方法后构形A位置及力矩模拟曲线如图3、图4所示。
结合图3、图4可知,传统的滑模控制器在初期会出现较大颤动,因此本文采用了一种新的自适应滑模控制器,该控制器不仅可对初值偏差进行补偿,还可在较小的时间段中得到预期的错误特性,从而对抖动进行有效抑制。通过对传统滑模控制器的跟踪偏差分析表明,该控制器具有很好的控制精度,但它无法按照实际情况对控制精度进行调节,具有很大的周期性偏差;由电动机的输出扭矩和联合估算的扭矩分布可发现,在使用滑模控制器时,电动机的转矩会出现显著颤动,从而使综合估算的扭矩出现较大颤动;在应用本文所提控制方法后,电机输出转矩和联合估计转矩的抖振明显减小,达到了理想的控制效果。通过实验证明,本文方法可对可重构模块机器人的关节运动进行良好的跟踪控制。
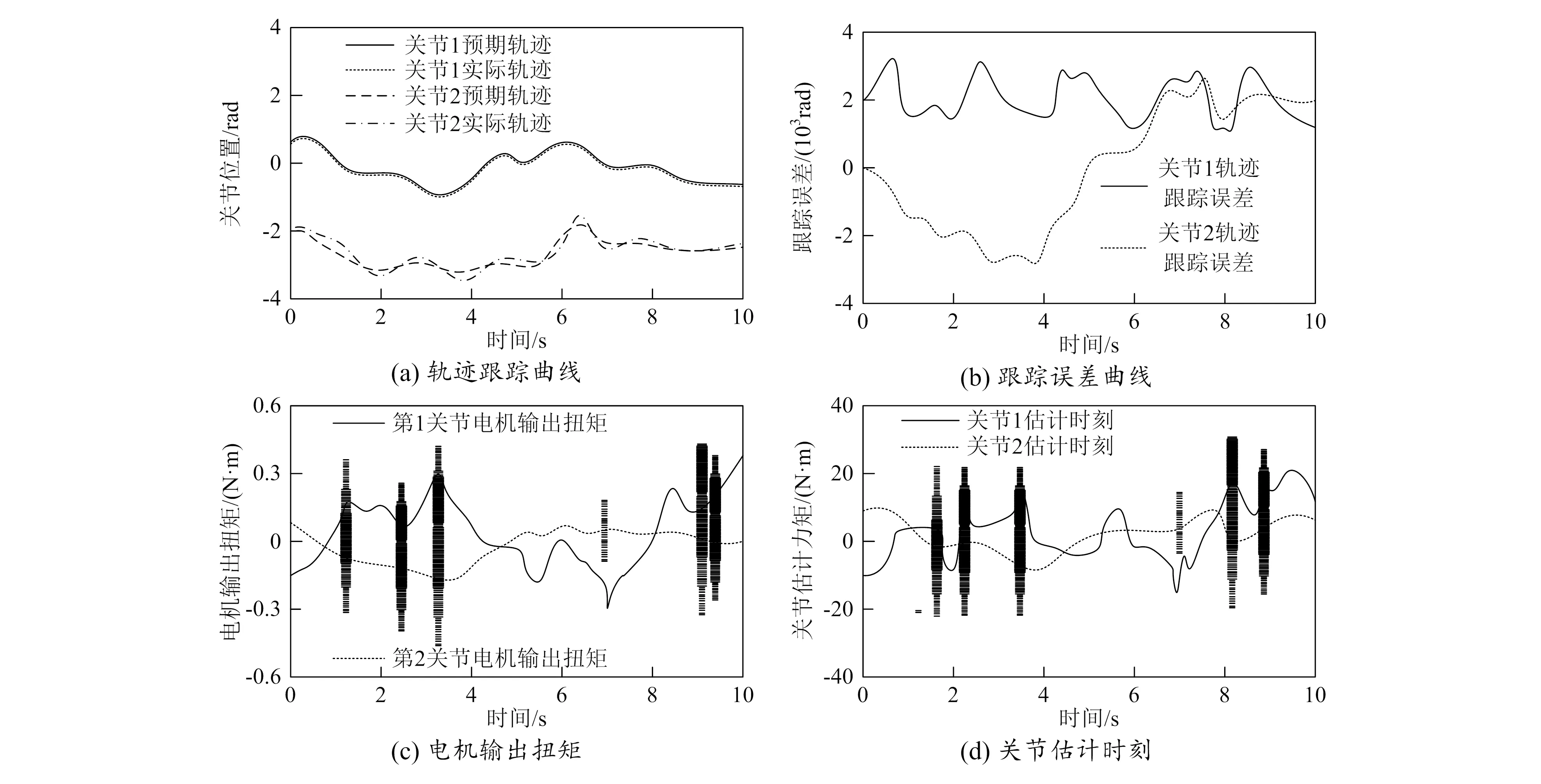
图3 应用传统方法后构形A位置、力矩曲线

图4 应用本文方法获得的构形A位置、力矩曲线
在结构B型铰链中,由于外部约束的作用,其关节位置和控制扭矩均为零。通过实验得到应用两种方法后构形B位置、力矩模拟曲线的结果,如图5、图6所示。
图6 采用本文方法获得的构形B位置、力矩曲线
由图5和6可知,这种滑模控制算法是行之有效的,而且在不改变控制参数的前提下有较好的适应性。

图5 采用传统方法获得的构形B位置、力矩曲线
采用本文方法获得的机器人末端约束力及轨迹追踪曲线如图7所示。

图7 采用本文方法获得的机器人末端约束力及轨迹跟踪曲线
由图7可知,在机器人末端受到外部约束力的情况下,所提出的方法能够有效实现机器人末端的运动目标,满足可重组模块机器人的可达性要求,取得了较好的控制效果。
4 结束语
可重组模块机器人是由一组带有标准连接界面的连杆组件和铰链组件构成,能够根据不同的工作环境,迅速装配出运动参数不同的机器人。本文针对现有机器人运动控制方法运动轨迹跟踪性能不佳、自适应能力差等问题进行研究,提出了基于动态约束下可重构模块机器人自适应滑模控制方法。实验表明,与传统控制方法相比,本文方法跟踪误差较小,且具有较好的适应性,在机器人末端受到外力约束的情况下可有效实现机器人末端运动目标,具有较好的应用效果,可为今后机器人运动控制研究与发展打下基础。
