非一致性条件下输沙对降水与径流的响应变化研究

陈 凯 吴彦昭 王巧娟

(1.甘肃省庆阳水文站，甘肃 庆阳 745000；2.甘肃省水文站，甘肃 兰州 730000；3.甘肃省陇南水文站，甘肃 陇南 742500)

河流水沙关系是河流生态环境研究的一个永恒课题，是河流生态治理保护与高质量发展的一项基础性研究。近40年来，由于我国经济高速发展，影响水沙关系的人类活动越来越频繁，主要体现在水土保持工程的大量实施、土地利用类型的改变等方面[1-2]。目前，国内学者对于河流泥沙的研究成果较多，如连秋晗等[3]对黄河佳芦河在生态治理影响下的水沙关系变化进行了研究，结果表明，与基准期(1957—1972年)相比,治理期(1973—2014年)的径流与输沙之间的关系在年尺度和次洪水尺度上均发生了显著变化,且径流输沙均显著减少；姚文艺等[4]、王鸿翔等[5]对黄河干流水沙长期关系进行了分析研究，结果表明，自20世纪60年代以来,黄河水沙变化经历了一个由“渐变”到“剧变”的过程，径流量、泥沙量大幅减少，且多数支流降水天然径流关系发生改变,而实测径流泥沙关系却未发生明显变化,即部分支流存在径流泥沙减少的“量”变与径流输沙关系“质”变之间的不协同现象；谢梦瑶[6]采用年值对黄河皇甫川流域水沙演变进行分析，对输沙量的减少量与同期降水量和径流量减少量进行了分析，结果表明，受气候变化及人类活动影响,皇甫川流域全时期(1954—2015年)水文要素平稳性受到破坏；赵阳等[7]对极端降水条件下水沙关系进行了分析，采用雨洪过程资料从短历时上进行分析，结果表明，相似极端降水条件下,水土流失治理后，韭园沟流域的径流模数和输沙模数较未治理的裴家峁沟流域明显减小,水土流失治理成效十分显著。但在水沙关系非一致性条件下流域内长期和短时均发生了变化，长期分析缺少输沙在雨洪过程中对降水和径流的响应分析，短时分析缺少对前期的降水和土壤状况进行考虑，因此在非一致性条件下研究输沙对降水与径流的响应变化关系十分必要。本文以长江西汉水流域为研究对象，在非一致性条件下研究输沙对降水、径流的响应变化，资料采用年、汛期、非汛期、月最大、日最大数据值，能够较全面、客观地进行综合分析。

1 研究区域概况

西汉水流域主要位于甘肃省西南部，在陕西省略阳县入嘉陵江，流域面积10178km2，甘肃省境内流域面积9785km2，河长212km。流域地貌上游主要以黄土丘陵为主，下游植被较好，以石山为主，是长江流域上游区的水土流失严重区、水资源短缺区，同时也是含沙量最大的区域。近年来，随着生态环境的改善、水土保持工程的实施，水土流失规模逐渐减少。

2 资料与方法

西汉水流域内有4处水文站，均有输沙、降水、径流等监测，西汉水流域水系及水文站点分布情况图1。本文收集了流域内水文站点近60年(1960—2019年)系列资料，选用西汉水干流下游控制站镡家坝水文站的输沙、径流，以及集水面积形心临近点平洛雨量站降水资料进行分析研究，对缺测资料进行插补延长处理。

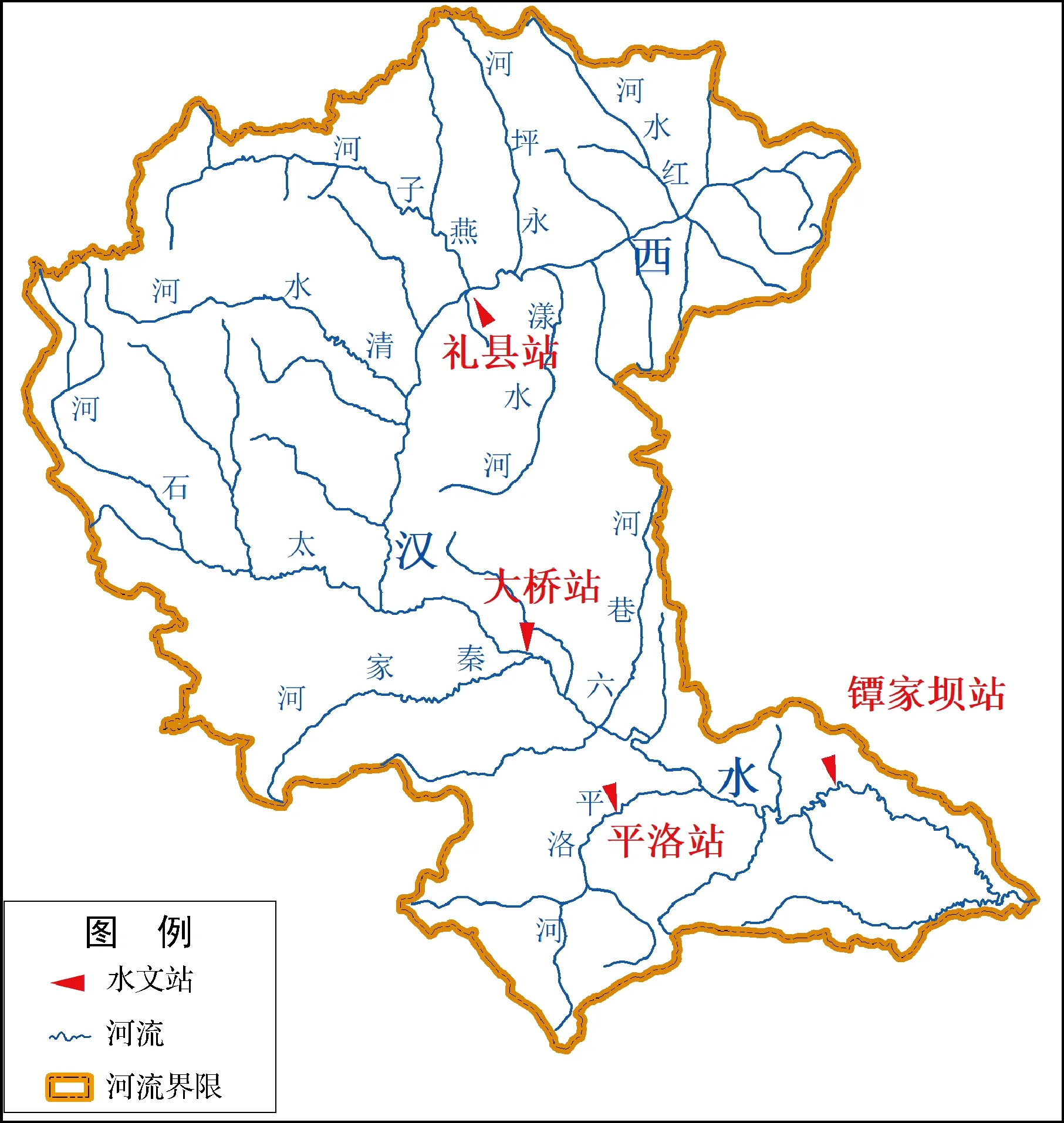
图1 西汉水流域水系及水文站点分布情况

3 水沙关系分析

3.1 多年变化分析

为了直观反映西汉水流域近60年的降水、径流、输沙变化过程，采用年降水量、年平均流量、年平均输沙率，作变率时序变化过程图，见图2。由图2可以看出，从整体上看，水沙变化具有一致性；年降水量、年平均流量和年平均输沙率均呈现减少趋势[8]。其中，1984年是建站以来洪水最大、年径流量最大、年平均输沙率较大的年份。从线性回归函数可以看出，年平均输沙率斜率(-3.0666)为负的最大值，其次为年平均流量(-1.2724)。采用坎德尔秩次相关法进行减少趋势显著性分析可知，年降水量显著性水平为1.332，减少趋势不显著；年平均流量显著性水平为3.014，减少趋势显著；年平均输沙率显著性水平为5.339，减少趋势显著。

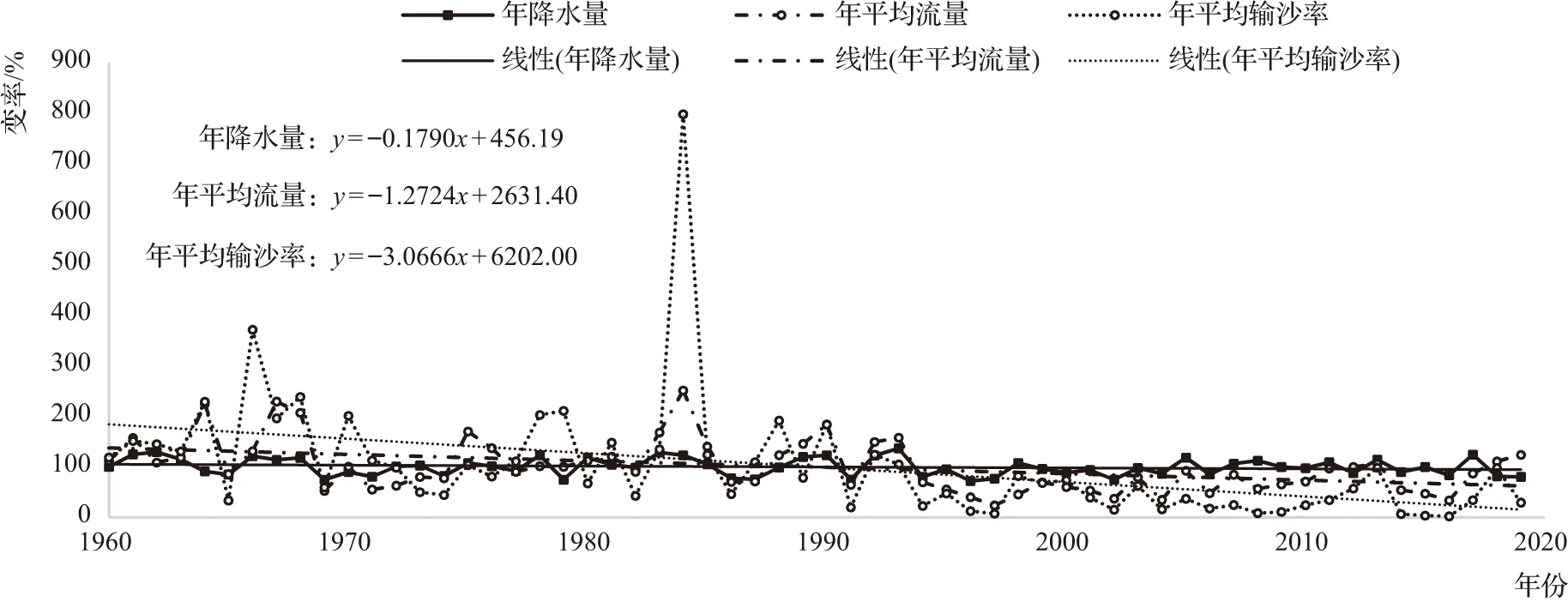
图2 相关要素变率时序变化过程

进一步对降水量、平均流量、平均输沙率的汛期(5—10月)、非汛期(11—4月)、全年、最大月值、最大日值分年代进行统计分析，结果见表1。从表1中可看出，1960—1969年的年降水量、年平均流量最大，1970—1979年的年平均输沙率最大，2000—2009年的年平均流量、年平均输沙率最小。从整体上看，1960—2019年的年降水量、年平均流量、年平均输沙率均呈逐渐减小趋势。降水量汛期、非汛期、最大月、最大日的均值最大值均出现在1960—1969年；平均流量汛期、非汛期、最大月的均值最大值均出现在1960—1969年，最大日的均值最大值出现在1970—1979年，其次为1980—1989年，均大于1000m3/s，可知极端洪水出现在这两个时段；平均输沙率汛期、最大月、最大日的均值最大值均出现在1970—1979年，非汛期的均值最大值出现在1960—1969年。

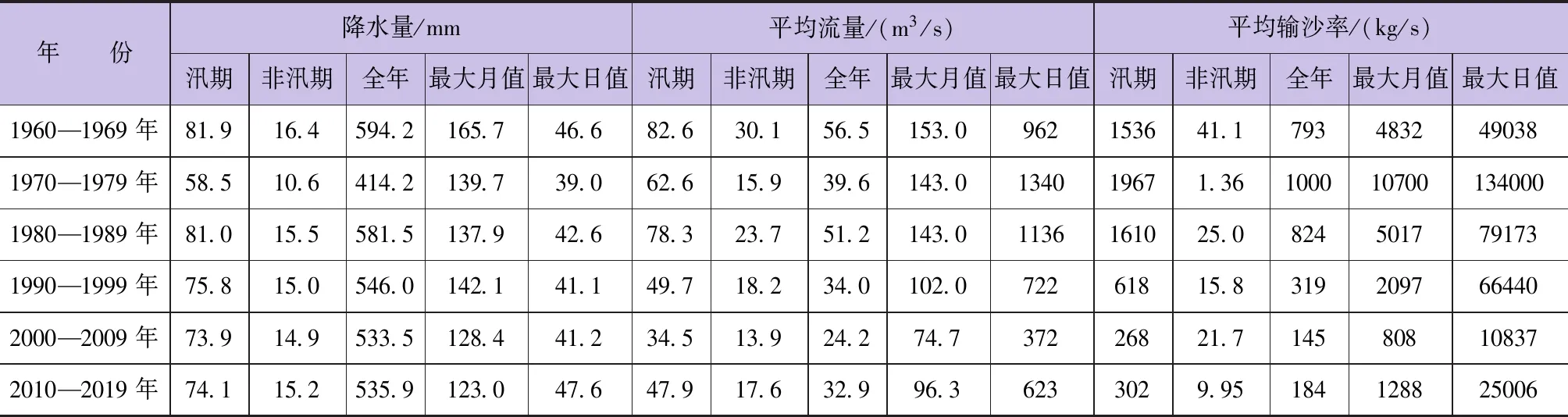
表1 相关要素不同特征值统计情况

3.2 一致性时段划分

受下垫面和全球气候变化的影响，输沙同其影响因素降水、径流系列发生突变，以突变点确定非一致性时间节点，划分一致性时段，是响应变化分析的基础[9]。因全年和最大月值具有一定的代表性，因此，对突变年份的确定，采用年降水量-年平均输沙率、最大月降水量-最大月平均输沙率、年平均流量-年平均输沙率、最大月平均流量-最大月平均输沙率双累积曲线进行分析[10]，汛期、最大日值不再作具体分析，降水、径流与输沙要素值双累积曲线见图3。由图3可知，突变年份出现在1993年，1960—1992年、1993—2019年为两个一致性时段，1960—1992年累积曲线的斜率远大于1993—2019年，说明西汉水在1993年以前输沙量较大，平均输沙率也较大。

图3 降水、径流与输沙要素值双累积曲线

3.3 相关性分析

水文分析中，在天然状况条件较好的情况下，降水量-输沙率、平均流量-输沙率关系视为线性关系。本文采用Pearson相关系数[11]、Correl相关系数对其进行相关性分析，相关要素不同特征值统计情况见表2。由表2可知，两种方法计算成果完全相同，降水量与输沙率的相关系数值较低，在0.28～0.41之间，其中最大日降水量与最大日输沙率相关系数最低，为0.28，说明降水量与输沙率直接相关关系较低；平均流量与输沙率的相关系数值较高，在0.40～0.73之间，其中非汛期相关系数最低，为0.40，说明平均流量与输沙率直接相关关系较高。

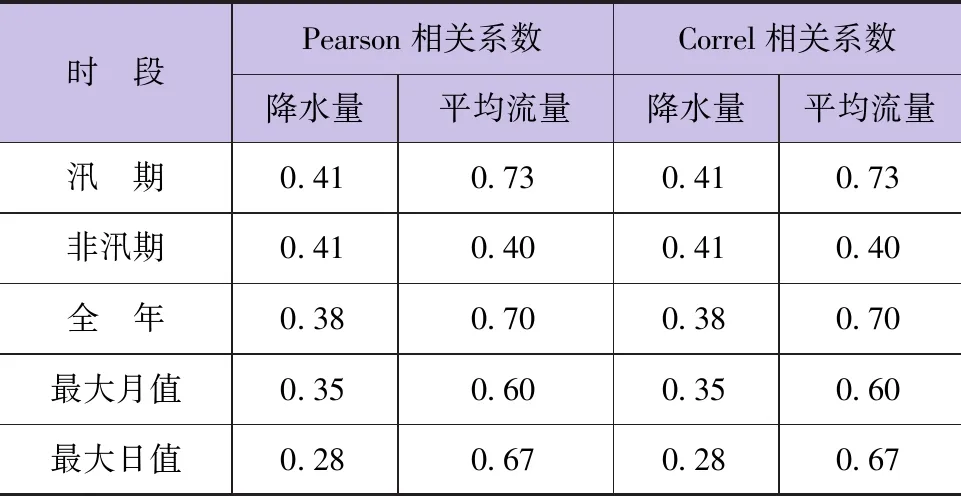
表2 相关要素不同特征值统计情况

3.4 输沙响应研究

如果在下垫面和气候条件一致的情况下，可视为水沙关系是相对稳定的，以这个思路建立输沙对降水、径流响应的数学模型[12]：

W=f(P,Q)

(1)

式中：W为输沙率，kg/s；P为降水量,mm；Q为流量，m3/s。

根据复相关3个变量以上存在线性和非线性相关两种形式，探究输沙对降水、径流两个因素共同变动的响应关系，同样假设两种数学模型，其中非线性变量最高取2次方，设计方程为

W=aP+bQ+m

(2)

W=a1P+b1Q+cP2+dQ2+ePQ+m

(3)

式中：a、b、a1、b1、c、d、e、m为常数参数。

假定不同的参数，将输沙、降水、径流按照年、汛期、最大月、最大日分别代入上述式中，求出最优参数。为了简化分析，选取时间长度具有代表性的年、最大月资料进行分析(一般汛期同年值基本相差不大，日值由于受前期水情影响较大，故不采用)。根据突变年份将系列分成1960—1992年、1993—2019年两个系列，分别建立方程式。

a.按照年值进行分析，利用线性相关性回归函数分析得出公式：

1960—1992年：

W=-0.1092P+11.930Q+77.94

(4)

1993—2019年：

W=-0.2983P+9.212Q+50.46

(5)

利用非线性相关性二次方回归函数求得公式：

1960—1992年：

W=0.6428P-2.607Q+0.0011P2+

0.0186Q2+0.1953PQ-62.51

(6)

1993—2019年：

W=2.893P-6.645Q-0.0036P2+

0.0024Q2+0.0724PQ-582.80

(7)

根据线性和非线性数学模型，对1960—2019年的年数据进行分析计算，将每年计算的年输沙率成果同原始数据进行对比分析，见图4。由图4可以看出，变化趋势基本一致，在特大值处模型值同实测值相差较大，相比线性相关数学模型，非线性相关数学模型同实测值变化峰型吻合度更高。

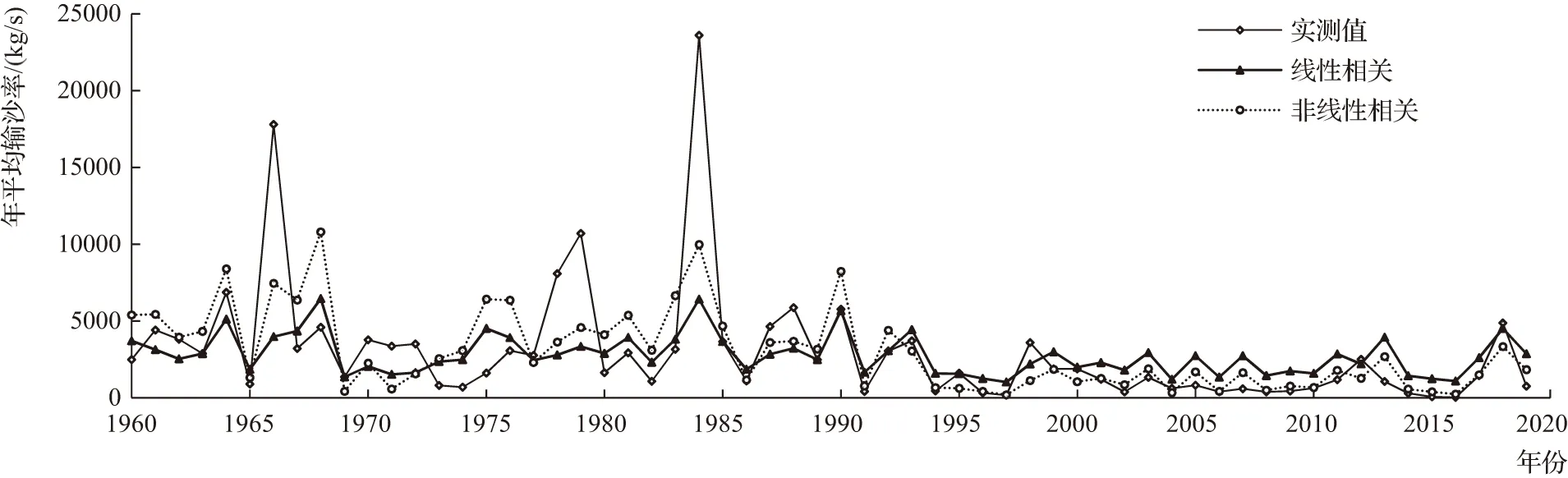
图4 年值数学模型分析值同实测值多年变化情况

为了进一步判断年平均输沙率对降水、径流响应关系模型拟合度，采用SSE(方差)、RMSE(标准差)、R-square(确定系数)3个参数进行分析，统计成果见表3。由表3可以看出，SSE、RMSE统计值远大于0，说明模拟成果较差；从R-square可以看出，1960—1992年数值更接近于1，说明该段的模型表征拟合度较好，1993—2019年数值与1偏离较大，说明该段的模型表征拟合度较差，但从整体上能够说明影响泥沙的因素较多，降水、径流是影响泥沙的部分因素，特别是在1993年以后，降水、径流影响程度减弱。

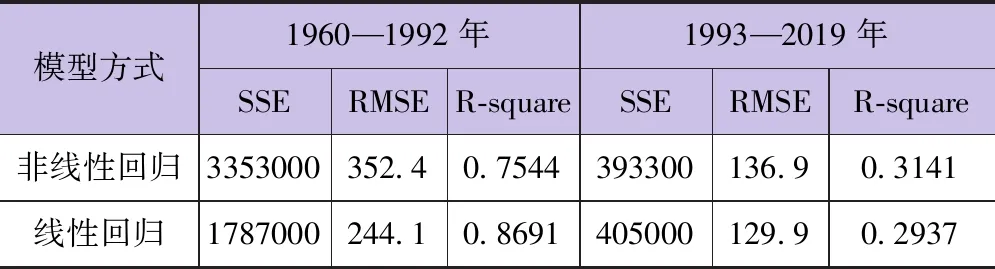
表3 年值数学模型分析值同实测值拟合度判别参数统计情况

b.按照最大月值进行分析，利用线性相关性回归函数分析得出公式：

1960—1992年：

W=0.4641P+19.22Q+530.5

(8)

1993—2019年：

W=4.968P+11.56Q-674.5

(9)

利用非线性相关性二次方回归函数求得公式：

1960—1992年：

W=-23.73P+35.89Q+0.3461P2-

0.4866Q2+0.1441PQ+690.3

(10)

1993—2019年：

W=-97.45P+67.18Q+0.5543P2-

0.5197Q2+0.0378PQ+3798.0

(11)

根据线性和非线性数学模型，对1960—2019年的最大月数据进行分析计算，将每年计算的最大月输沙率成果同原始数据进行对比分析，见图5。由图5可以看出，变化趋势基本一致，在特大值处模型值同实测值相差较大，相比线性相关数学模型，非线性相关数学模型同实测值变化峰型吻合度更高。

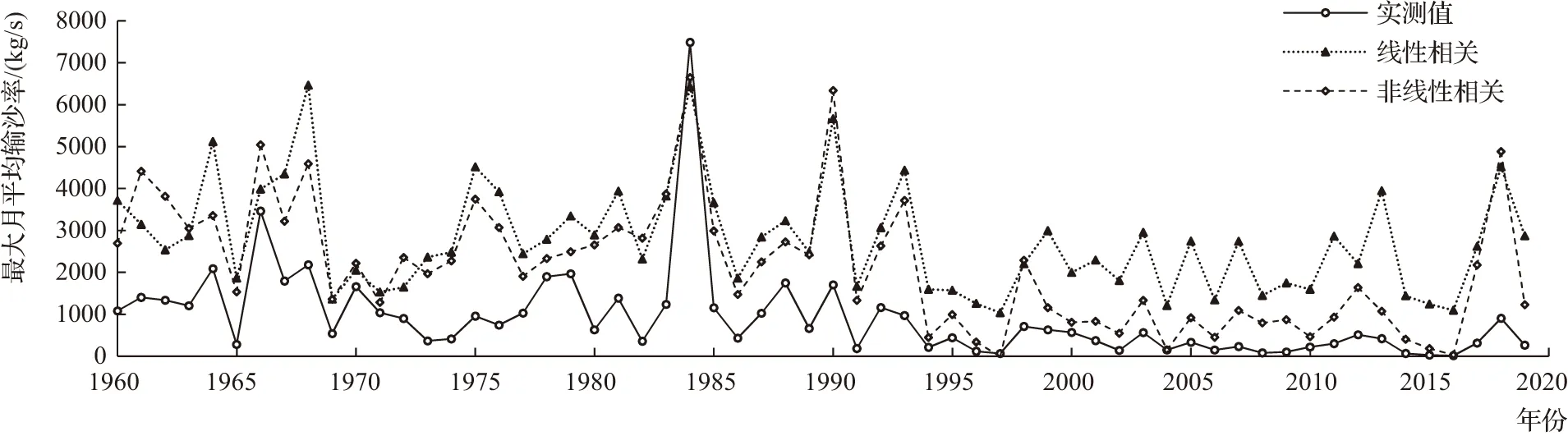
图5 最大月值数学模型分析值同实测值多年变化情况

最大月平均输沙率与最大月降水量、最大月平均流量响应关系模型分析值，同实测值判别拟合度3个参数成果统计情况见表4。由表4可以看出，SSE、RMSE值远大于0，同年值情况基本相同；从R-square可以看出，最大月值1960—2019年均较接近于1，说明该段的模型表征拟合度较好，较年值拟合度更好。

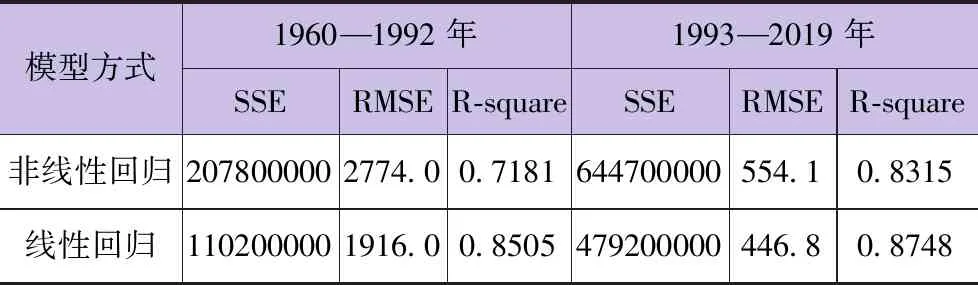
表4 最大月值数学模型分析值同实测值拟合度判别参数统计情况

4 结 语

本文选取长江上游输沙量较大河流(西汉水流域)进行非一致性条件下输沙对降水与径流的响应变化分析研究，通过对降水量、输沙率、流量的年值，汛期、非汛期、最大月值、最大日值的多年变化情况进行分析，表明该流域水沙整体呈减少趋势，降水减少趋势不显著，径流、输沙减少趋势显著；突变年份为1993年；流量同输沙率相关程度高于降水量同输沙率相关程度；相比线性相关数学模型，非线性相关数学模型与实测值变化峰型吻合度更高，因此今后宜用非线性数学模型对输沙响应变化进行研究。

受下垫面和全球气候变化的影响，区域内水沙关系发生了改变。对水沙关系的研究方法较多[13-14]，水文监测数据分析是一种比较传统的方法，输沙情况受到的影响因素较多，仅通过对降水、径流的响应变化进行分析研究，还存在一定的局限性，后续可加入植被覆盖、水利工程等相关资料进行更加全面地分析研究。