基于GWR模型的苏州市住宅价格空间分异与影响因素研究

朱 进，徐 昱，张委伟，李晨映

（1.苏州科技大学 地理科学与测绘工程学院，江苏 苏州 215009；2.中国科学院 地理科学与资源研究所，北京 100101）

自1998年住房制度改革以来，我国住房市场逐渐开放，计划经济体制下的住房福利分配逐渐被商品化住房取代，释放了巨大的住房消费，推动房地产业进入了长久的高速发展期，并渐渐成为国民经济的支柱产业。随着我国城市化的快速发展和相对宽松的货币政策等因素的影响，大城市中住宅价格迅速上涨，住房供需矛盾不断激化。高房价带来的影响涉及社会的方方面面，并将通过影响人才居留进而影响城市未来的竞争力。因此，城市住宅价格的影响机制亟待被进一步研究和剖析。

目前国内对住宅价格分异的研究主要以北京、上海、广州、深圳、长春等一二线城市为主[1-4]。其研究方法可以归结为两类：一类利用GIS技术和地统计分析，对住宅价格的空间分布规律进行探究，包括运用空间自相关、趋势面分析、空间插值等方法来定量刻画城市内部住宅价格的空间分异特征；另一类通过量化方法分析影响住宅价格分异的各个因素，在供需视角下，从需求方和供给方对住宅特征的市场均衡角度出发构建出的特征价格模型[5]。目前，基于最小二乘法（OLS，Ordinary Least Squares）的特征价格模型（Hedonic Model）得到了广泛应用，是目前国际公认的研究住宅价格机制最主流的方法。但住房特征价格模型基于空间均值的假设，缺乏对变量空间异质性的解释，忽略了不同地区住宅价格形成的特殊性，导致空间异质性的考虑不足[3-4]。地理加权回归（GWR，Geographically Weighted Regression）模型考虑不同因素的空间异质性，并被广泛运用在住宅价格及土地价格影响因素等研究领域[5-11]。近年来，已有一些文献研究基于GWR模型的城市住宅价格的影响因素与内在机制，但总体上仍相对不足。

苏州市是江苏省内人口最多和GDP最高的城市，其地处长三角中部，东临上海、南接嘉兴、西抱太湖、北依长江，是首批国家历史文化名城之一，有“人间天堂”的美誉。在空间结构分布上，苏州市中心城区由姑苏区、工业园区、吴中区、吴江区、虎丘区、相城区组成，与张家港、常熟、昆山和太仓等城区形成了明显的一主多副的空间分布结构，但相对主副城关系紧密的南京、无锡、杭州、嘉兴等城市，苏州市的主副城之间的关系较为松散。其中，张家港与无锡关系较为密切，而昆山、太仓与上海的关系较为密切。在经济上，苏州各区人均GDP均高于全国平均水平，其中，工业园区连续多年保持最高。除此之外，2020年苏州市总GDP首次突破2万亿元，成为了我国第六个2万亿元城市，近年来城市房价也在迅猛增长。据笔者所知，目前还没有利用GWR模型探讨苏州市住宅价格的相关研究。利用GWR模型，以苏州市2020年住宅价格数据为例，从社区属性、交通区位、商业区位三个方面出发研究苏州市住宅价格的空间分异，探究苏州市内住宅价格的影响因素的空间分布规律，以期为房地产管理部门深入了解城区住宅价格分布状况，进行区域房价调控提供依据，并为政府规划部门未来制定和实施相关政策提供参考。

1 数据来源与研究方法

1.1 数据来源

论文研究对象为2020年的苏州市内住宅小区，总计为3 671个。研究数据来自链家（https：//www.lianjia.com）和安居客（https：//suzhou.anjuke.com）网站，通过Python爬虫程序抓取。剔除信息严重不完整、明显有误的数据之后，利用SPSS的统计分析功能，通过对样本数据进行正态性检验和共线性检验，将出现变异的样本筛选去除，得到剩余样本1 710个。数据包括住宅小区的小区名称、小区均价、楼龄、容积率、绿化率、住宅套数、总户数等属性信息。以住宅小区为研究对象，可以避免一般住房与别墅、保障性住房等不同社区问题，以及户型朝向、装修程度等个性化差异造成的价格异常，增加结果的可靠性。住宅小区经纬度坐标信息通过高德地图获取，经过地理编码转换后得到坐标，将以上属性信息与住宅价格数据进行关联，建立住宅小区空间数据库，如图1所示。

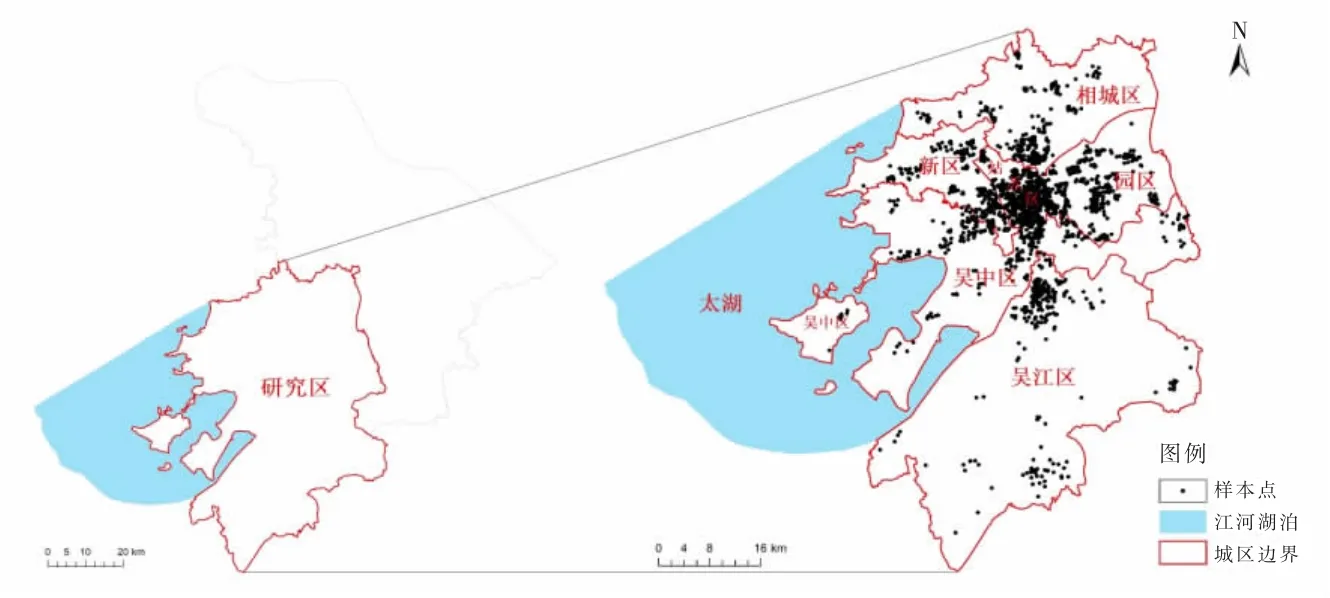
图1 研究区范围与样本小区

1.2 研究方法

特征价格模型认为商品的价格是由不同特征变量的隐含价格共同决定的，通过建立模型的方法可以将各个特征的隐含价格分离显示，而OLS回归是特征价格模型的一种分析方法，通过OLS模型可以对因变量与解释变量的关系建立线性回归模型[12-13]，常用于解释自变量与因变量的相互依存关系，基于OLS方法对参数进行估计，其基本形式为

式中，γi为在观测点i的因变量值，xik为在观测点i的第k个自变量，β0为模型的截距，βk为k个自变量的回归系数，εi为随机误差，服从N（0，σ2）分布。

该模型仅仅是对参数进行了平均或全局意义上的估计，很难体现参数在空间上的非平稳性。

地理加权回归是一种改进的空间线性回归方程，与传统的回归模型相比，该模型引入地理位置信息，容许局部而不是全局的参数估计[14]，其可以在任何一个选定的变量上，用数据的局部子集构建一个回归模型，使得数据包含在这个局部模型中，进行空间加权，权重的大小取决于空间的相邻程度和相互位置。同时，该方法可以把空间权重矩阵应用到线性回归模型中，从而形象的表现出空间结构分异[15]。其优点在于对普通回归方法的扩展，具有快速调节空间权重的功能，模型中的系数可以更好地反映各个要素的差异性和非均质性。因此，研究房价空间分异及其影响要素时，使用GWR模型相对于计量方法如一般线性回归效果更好。GWR模型表达式为

式中，（μi，vi）为样点i的坐标，β0（μi，vi）为回归常数，βj（μi，vi）为第i个样点的第j个回归值，εi为随机误差值。

文中，采用AICc准则确定带宽，并采用自适应带宽的方法来确定最优带宽，公式为

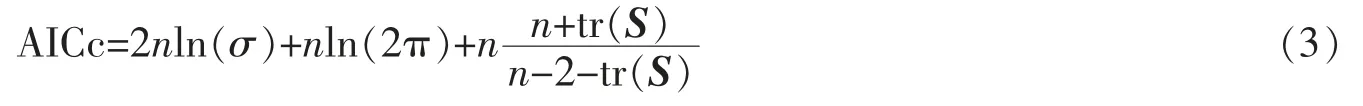
式中，AICc为修正的赤池信息准则，n为样本点数量，σ为误差估计项的标准离差，tr（S）为GWR的S矩阵的迹。

2 苏州市住宅价格影响因素研究

2.1 变量选取

在宏观或微观区位上，区域住宅价格均受到众多因素的影响，但住房的价值主要由自身结构特征、区位特征和公共服务设施便利性构成[16]。借鉴国内外相关研究中住宅价格影响因素的选取和量化方法[17-18]，根据GWR模型的变量要求，将已有数据根据属性划分为三类：社区属性（楼龄、容积率、物业管理费、绿化率），交通区位（周边公交站点总数、最近地铁站距离、最近学校距离、最近医院距离、CBD距离），商业区位（休闲娱乐、住宿服务、餐饮设施、购物中心、办公写字楼、金融大厦的数量），以求更细致地分析住宅价格影响因素的作用机理。由于商业区域通常包含大量餐饮、购物、娱乐等服务设施，因此引入综合各类服务设施转换的周边地块功能混合度作为评价指标，避免多种因素交错带来的复杂性和不确定性。借鉴信息熵的表示方法，地块的功能混合度计算公式为[19]

式中，H表示功能混合度，Pi是功能i的概率，用功能为i的POI数目除以该地块的各类POI数目总和表示。熵值越大，表明该地块混合度越高，周边配套设施程度越丰富，功能混合越均匀。在文中，混合度的计算首先将研究区范围划分为300 m×300 m的网格（街区范围）作为地块，然后将服务区位五类设施（休闲娱乐、住宿服务、餐饮设施、购物中心、办公写字楼）的POI数目空间连接至地块要素中，计算每个地块中各类设施POI的个数，最后计算每个地块中所有POI个数的总和和占比，依据公式计算熵值即可得到各地块的混合程度。将地块内所有小区单元与地块关联即可得到各小区的混合程度。从计算结果来看（如图2所示），苏州市功能混合度的空间分布特征呈现明显的“一主多副”结构，与相关研究[20-21]吻合度相当高，表明这一结果较为合理。

最终，得到10个与住宅价格有关的控制变量（见表1），利用SPSS对变量之间是否存在多重共线性进行检验，显示容差全部小于或等于0.1且自变量的方差膨胀因子（VIF，Variance Inflation Factor）值全部都大于或等于10，表明10个指标都可以作为商品住宅价格的影响因素。

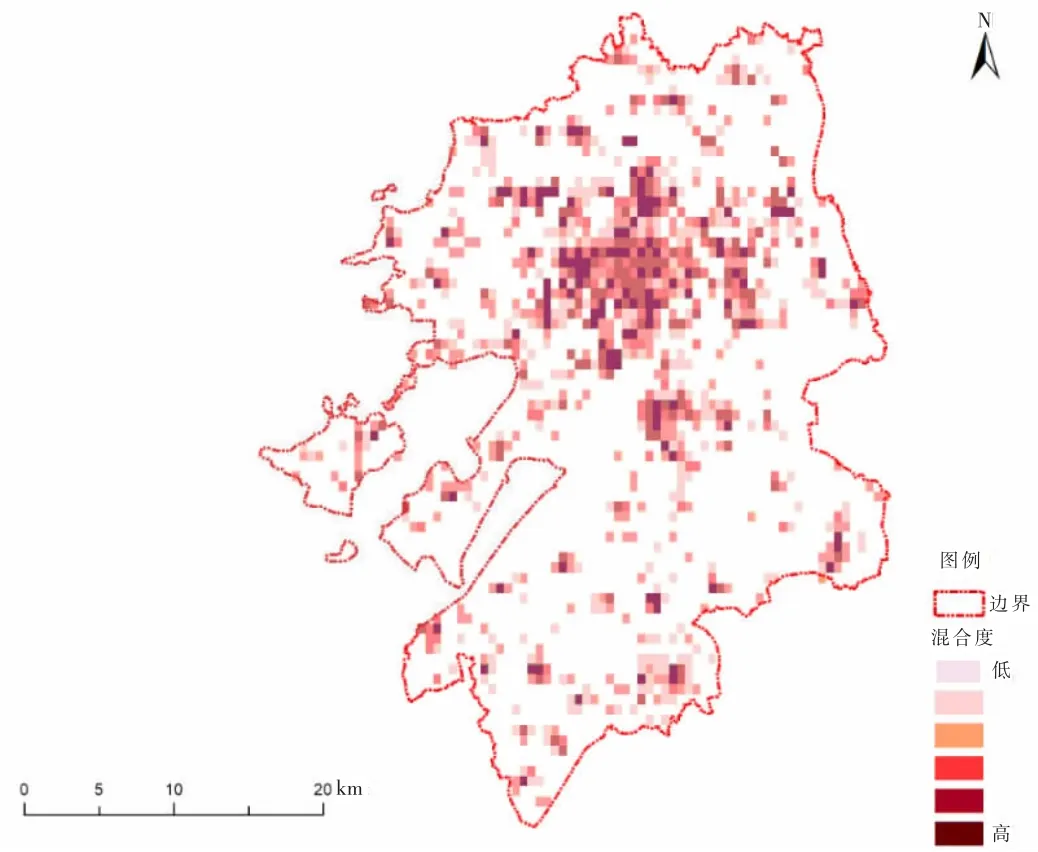
图2 功能混合度分布

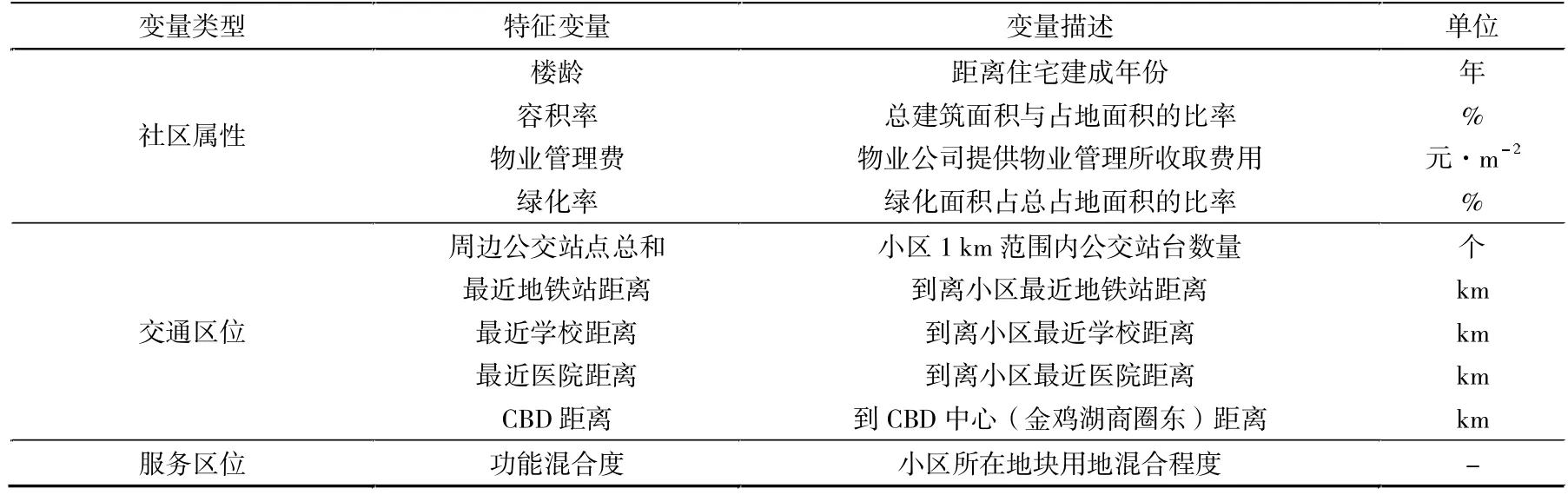
表1 变量选取与描述

2.2 模型构建

依据GWR构建模型，以自适应的高斯函数为核函数，黄金分割法作为带宽搜索方法，通过修正的赤池信息准则（AICc）方法计算带宽，运用ArcGIS软件计算得到OLS模型和GWR模型的相关参数，并且对两个模型的分析结果进行比较。由表2可知，OLS方法整体上显著，但是OLS残差的检验结果（Moran’s I指数验证）呈空间自相关，表明OLS的回归结果存在较大的误差，基于OLS方法的全局模型不合适。GWR模型的拟合优度（R2）大于OLS模型，并且GWR的残差平方和和标准差相比OLS模型均有明显下降，赤池信息准则和OLS方法比下降了14.2%。综上，基于GWR模型的空间回归分析方法有效缩减了残差，显著提升了模拟精度，最优带宽值亦显著改进，故笔者使用GWR方法分析苏州市住宅价格的影响因素。

表2 OLS与GWR结果对比

GWR得到的结果是各影响因素对每个样本生成的一个特定系数，即回归系数，将得到的数据进行统计和汇总，见表3。对回归系数进行对比可以看出，住宅价格的回归系数在表格中显示为有正有负、有大有小，但是差距不明显，说明各个影响因素都是存在的，形成的影响效应有高有低。

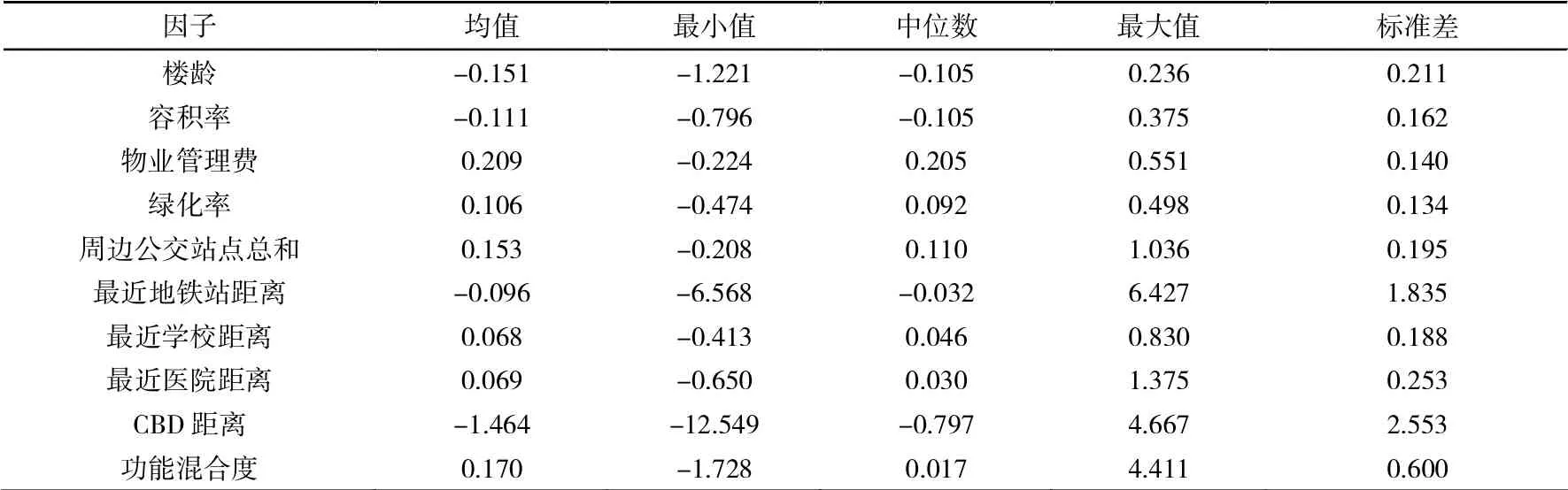
表3 GWR模型回归结果

3 结果分析

3.1 社区属性

楼龄因素总体呈现对房价的负向影响，如图3（a）所示，说明正常情况下楼龄越大，住宅价格越低。在工业园区和高新区内楼龄对住宅价格的影响系数为负，可能原因是作为近年发展重心的两区新楼盘较多，价格较高，在这两个区域内的老楼价格会低一些。在姑苏区内则存在一些楼龄的影响系数为正向的聚集区域，结合姑苏区内重点学校地理位置来看，系数为正的小区大都位于重点学校附近，小区内房价受学区房属性影响要明显高于同类小区均价，这与南京市内“教育型”设施逐渐成为居民购房行为的重要影响因素相似[22]，即城市点状公共设施例如医院、小学、幼儿园等对住宅地价的负向效应有扩大趋势。另外，楼龄的影响力相对减弱。结合现实情况，姑苏区作为古城区，其内新楼盘较少，住宅价格对于楼龄的敏感度本就应该偏低。

容积率具备显著的负向影响，其总体系数分布反映为中心城区周边较强而其他区内较弱，如图3（b）所示。结合苏州市政府近年不断启动市区城中村和旧城区改建项目的情况来看，苏州市中心城区内影响系数较大的小区大都是具有学区房属性的老小区，由于建筑密度和绿化率的因素，小区容积率偏高，然而学区房特性又决定了它对特定购房人群的必需性，在居住环境质量相近的情况下，容积率的高低成了很关键的衡量因素，因此区域内容积率的影响系数相对于其他地区更大。

物业管理费总体呈现对房价的正向影响，即物业管理费用越高，住宅价格越高。说明对于大部分小区住宅，物业费越高，住宅价格越高。系数最大值区域主要出现在城区边界附近，如图3（c）所示。原因可能是其离中心城区较远，开盘小区住宅价格大多较低，物业费对住宅价格往往会起到重要影响。回归系数为负值的区域则主要是苏州市内的封闭式高档住宅区，住宅价格对物业费这类管理服务因子敏感性较弱，因此系数大多趋向于0或为负值。

绿化率对房价的影响表现为正向影响，即绿化率越高，住宅价格越高，其中系数为负数的区域主要为太湖景区周边和姑苏古城区内，如图3（d）所示。太湖景区周边住宅对于绿化的需求上本身就已经达到满足，因此对于绿化率的需求相对较低。苏州城区内公园较多，且有金鸡湖和石湖等大型湖区，系数为负的区域主要集中在这些小区，小区周边绿化条件优良，小区内的绿化率对房价的影响力相对较弱。

3.2 交通区位

1 km半径内公交站台数量对城市住宅价格的影响呈现出正向关系，如图3（e）所示。即1 km半径内公交站台数量越多，住宅价格越高。值得注意的是，当住宅离中心城区距离超出一定范围后，影响系数逐渐变小，考虑到距离较远的区域前往中心城区的出行成本已经很高，住户对于交通便利的需求性远低于平均值，因此偏远城区对于交通区位的敏感性要远小于中心城区及其邻近区域。

到最近地铁站的距离整体上负向影响房价，距离地铁站越远房价越低，值得注意的是中心城区内大部分住宅小区的影响系数趋向于0，即距离地铁站距离的远近对于房价近乎没有影响，如图3（f）所示。其原因可能是中心城区内地铁站相对较多，许多小区距离地铁站的距离在1 km以内，而这些小区大多都是老小区或者旧大厦，楼房质量偏低，且商业设施大多邻近地铁站，居住环境也相对嘈杂。另一方面这些区域公交站点较多，对地铁的依赖相对较小。而周边区域如吴江区集聚在地铁线末端，离中心城区比较远，对地铁更为依赖，因此距离地铁越远房价越低。

CBD距离整体上表现为较为明显的负向影响，即距离CBD中心越远房价越低。其最显著的表现在工业园区，该区域内影响系数为负数且绝对值最大，如图3（g）所示，而高新区内和吴江区内部分住宅小区的系数正向，原因可能是这些区域距离CBD距离超出10 km，CBD距离对其影响较小。与南京市相比[23]，苏州市CBD中心对于房价的影响系数更大，一方面可能是苏州市新的CBD中心确立时间较短，其对于周边的辐射影响还没有明显见效，次级商业中心的数量和规模都还没有得到扩大，在一定程度上增强了CBD对地价的影响程度；另一方面，苏州市的新建地铁线更加完善了城市交通路网，进一步扩大了CBD对地价的影响范围，加强了影响力。

3.3 服务区位

如图3（h）所示，功能混合度的影响力体现出距离衰减的特征，具体表现为功能混合度在中心城区呈现正向影响，而随距离中心城区越远影响力逐渐衰弱，到偏远城区对住宅价格的影响已经呈现出负向影响。结合图2看，功能混合度的分布呈现“一主多副”的分布特征，中心城区经过长年的更新和发展，功能混合度非常高，已形成高度复杂而稳定的功能布局。偏远城区总体功能混合度偏低，但区域内已经存在部分高功能混合度的聚集区域，表明该地区的发展正日渐成熟但仍需时间发展。因此，偏远城区当地住户的消费和娱乐等日常需求更偏向于前往功能设施多样且完善的中心城区解决，对于住宅小区周围的功能配套设施需求并没有那么强烈，导致偏远城区住宅价格对周边配套设施的敏感性较弱。

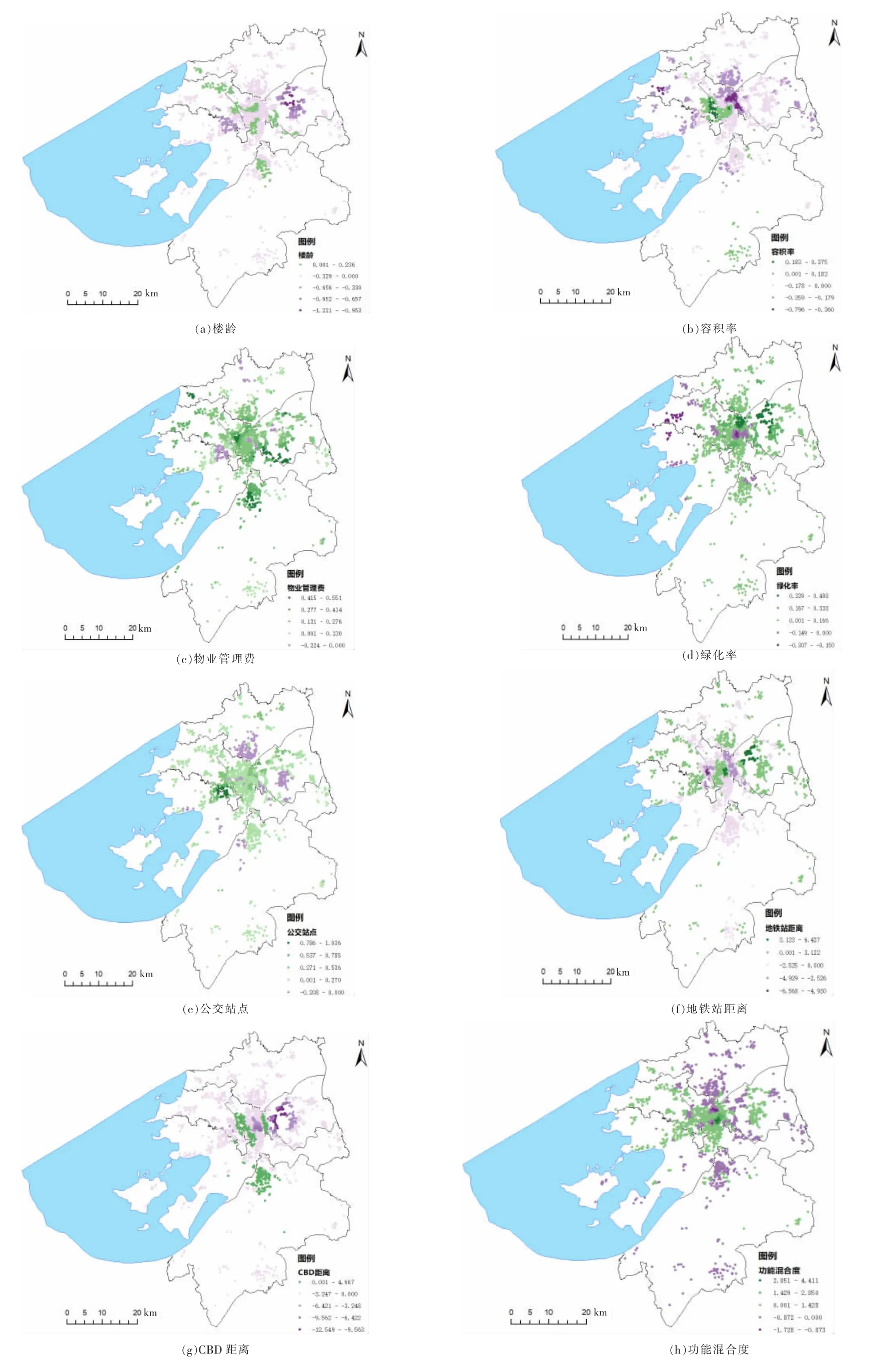
图3 GWR模型回归系数的空间分布

4 结语

通过将地理加权回归模型应用于实证研究中，结合苏州市2020年房价数据，对苏州市内住宅价格的空间分异和其影响因素进行研究，主要结论有：

影响苏州住宅价格及其空间差异的因素多样，其中因素按其影响力从大到小分别为：CBD距离、物业管理费、混合度、周边公交站点总和、楼龄、容积率、绿化率、最近地铁站距离，CBD距离的平均影响力是所有变量中最大的，接近于1.5。

住宅价格影响因素存在显著的空间异质性，各影响因素在城市不同区域对住宅价格的影响尺度存在差异，其中中心城区受CBD距离、最近地铁站距离等传统特征因子影响较大。偏远城区则主要受物业管理费、混合度影响，形成近似带状或块状的分布。

CBD距离、物业管理费、功能混合度等体现住房消费者收入能力、居住环境诉求、生活方式的要素，成为最具房价影响力的影响因素，表明城市房价分异与居住群体的空间分异存在着一定的联系。住宅价格影响因素的空间异质性表明根据社区档次和类型的不同，住房消费群体的经济社会属性也会不同，由此导致不同社区内住户对房屋属性需求的不同，各类影响因素因此在不同区域呈现不同的影响力，使城市房价与居住分异在一定程度上表现为空间结构的关联性[22]。

由于数据的局限性，影响因素在时间尺度上的空间差异有待补充，未来可从时间和空间两个方面进行探究，全面分析苏州市房价影响因素的时空异质性，为各区域制定不同房价调控政策提供更加科学的依据。同时已有的研究没有纳入具体的学区变量，因此无法具体讨论这些因素的影响。最后，在住宅价格影响因素方面的筛选中，不可避免带有部分主观因素，不能做到完全的客观。今后的研究还需在影响因素的划分上进一步的细化，以深入分析住宅价格空间分异及影响机制。