一种基于动态解相的高反射率表面三维测量方法

严海源，杨延竹，李 恒

(东华大学 机械工程学院，上海 201620)

光栅投影三维测量方法具有速度快、非接触、数据易于存储以及精度高等优点[1]，但是该方法的应用与被测物体表面的光学反射特性密切相关。对于高反射率物体而言，由于其表面部分反射区域特性存在巨大差异，将导致图像部分饱和像素区域的解算相位不准确，为部分曝光不足的像素带来较低的信噪比[2]。高反射率物体表面给光栅投影三维测量方法的应用带来很大困难。

目前为了降低因饱和像素导致的解算相位误差，国内外研究人员对高反射率物体表面的三维重建方法进行了大量的研究[3-10]。例如：Zhang等[6]提出一种基于多重曝光的光栅投影三维测量方法，拍摄一系列不同曝光时间的条纹图像，通过筛选每个像素处灰度值最大的非饱和强度组成高动态范围(high-dynamic range,HDR)图像。Waddington等[7]提出一种投影正弦条纹图案技术，通过不断调整投影仪的曝光时间，拍摄一系列不同投影亮度的相移图像，并从中选择灰度值最大的非饱和强度像素合成HDR图像。Feng等[8]通过偏振和多重曝光法相结合，即将两个正交偏振滤光片分别添加在相机和投影仪前面，再结合多重曝光来进行测量。Chen等[9]提出一种饱和式相移图技术，设置相移步长N等于一个相位周期编码列数的整数倍或设置10步以上，都能保证高反射率物体表面点云的重建质量。雷彦章等[10]提出一种单、双目结合的光栅投影三维测量方法，采用双目测量进行点云重建，同时利用两个单目的重建结果对双目重建中的点云孔洞区域补缺，以此来解决因过曝导致的点云孔洞问题。

上述方法主要通过拍摄多组曝光图像和不断调整投影条纹图案的对比度合成HDR图像，其曝光时间依赖于经验，难以满足实时测量的要求；采用饱和式相移或多步相移进行测量的耗时较长，单、双目结合的三维测量步骤复杂，不利于应用实现。

本文提出一种基于动态解相的高反射率表面三维测量方法，引入过曝因子判断像素是否饱和，使得相位解算时参与计算的相移图的数量不同，从而滤掉因过曝而带来的相位误差，在保证点云重建质量的同时，缩短测量时间且便于应用实现。

1 动态解相的高反射率表面三维测量方法

基于动态解相的三维测量方法主要利用光栅投影进行测量，测量原理如图1所示。

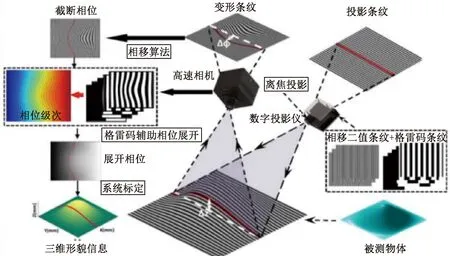
图1 光栅投影测量原理图Fig.1 Grating projection measurement principle diagram

动态解相的三维测量方法实现步骤如下：

(1)在数字光线处理(digital light processing，DLP)投影仪中烧录计算机生成解算相位所需的正弦相移条纹图和格雷码图，并标定投影仪与相机的位置关系。

(2)分别投影正弦相移条纹图和格雷码图至被测物体表面，在投影的同时用相机采集图像，组成一组解相图集。N步相移法主要通过N幅正弦相移条纹图来解算相位，条纹图如式(1)所示。

Ii(x,y)=I′(x,y)+I″(x,y)·

cos[φ(x,y)+σi]，i=1,2,…,N

(1)

式中：Ii(x,y)为第i幅正弦相移条纹图中(x,y)像素坐标处的光强；I′(x,y)为该像素坐标处的平均灰度值；I″(x,y)为该像素坐标处的条纹幅值；φ(x,y)为待求物体包裹相位；σi为相移大小；i为相移步数。

动态解相采用改进后的N步相移公式求解包裹相位，其推导过程如下：

Ii(x,y)=a0(x,y)+b(x,y)cos[φ(x,y)]·

cosΔφi+b(x,y)sin[φ(x,y)]sinΔφi

Ii(x,y)=a0(x,y)+a1(x,y)cosΔφi+

a2(x,y)sinΔφi

(2)

式中：a0(x,y)=I′(x,y)；b(x,y)=I″(x,y)；a1(x,y)=I″(x,y)cos[φ(x,y)]；a2(x,y)=I″(x,y)sin[φ(x,y)]；Δφi=σi。

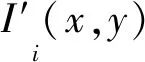
(3)

式中：ε为偏差平方和；δi(x,y)为过曝因子，

由于环境光等全局光照的影响，这里灰度阈值设置为250，判断每幅相移图的像素灰度值大于等于250即被认定该相移图像素位置过曝。相机饱和像素导致相移法解相的不准确，主要因为该像素位置的物体表面区域反射的光强大于相机的光强量化等级。遍历位于同一像素点的每幅相移图，由于同一像素点的每幅相移图的灰度值存在差异，大于等于灰度阈值的像素点判断为过曝，则将δi(x,y)值设置为0，从而因过曝而带来相位误差的点不参与计算，即每个像素点参与计算的相移图数量是不同的动态解相。而传统方法解算相位不管该像素点是否存在过曝的相移图，采用所有的相移图全部参与计算相位。

(4)

(5)

(6)

式(4)、(5)和(6)存在a0、a1、a23个未知变量，解算相位主值需要3个方程，意味着相移步数小于3步则解算不出相位值。由于在一个相位周期内的相移图上某一像素点的灰度值可能均≥250，即δi(x,y)过曝因子赋值为0，此时参与计算的相移图数量少于3张，因此解算不出该像素点的相位主值。为防止出现解算不出相位主值的情况，设置了以下策略：

判断每幅相移图上的某像素位置的灰度值是否大于等于灰度阈值，设置某相移图上的某像素的过曝因子值。当参与计算的相移图数量少于3张时，设置一个临时变量存储该像素点相移图信息，将其用于查找未过曝的相移图。正弦条纹示意图如图2所示，通过观察图2中P点的灰度值大于250即处于过曝状态，将正弦条纹1相移π之后得到与之反向的正弦条纹2，此时P′点处于与P点最远处，即P′点最可能处于不过曝状态，将由相移π之后的P′点灰度值代替P点灰度值参与计算。

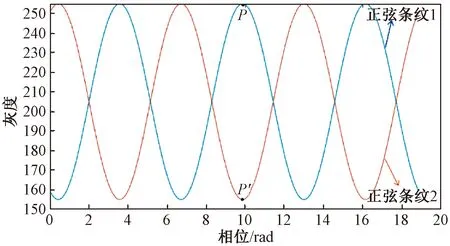
图2 正弦条纹示意图Fig.2 Schematic diagram of sine fringe

因每幅相移图某像素位置处的灰度值不同，即δi(x,y)值不一样，该像素位置相位解算时参与计算的相移图信息和相移图数量不一致，因此过曝因子未能消掉。将式(4)、(5)和(6)化为矩阵形式，如式(7)所示。

(7)

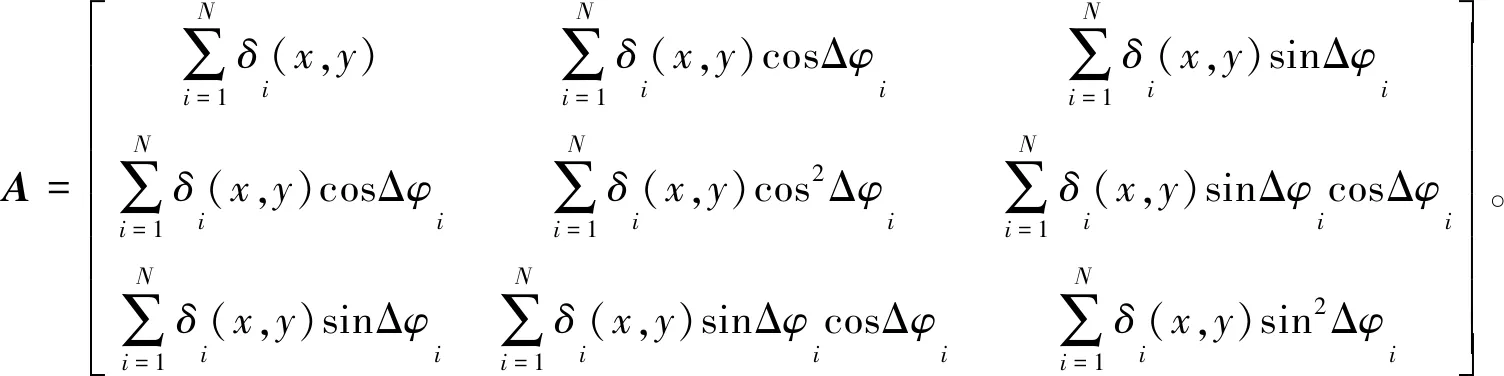
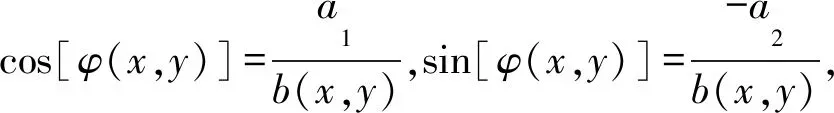
φ(x,y)=arctan(-a2/a1)

(8)

(6)DLP投影仪将格雷码图案投射到物体上，利用相机捕获被深度调制后的6张格雷码图案。通过对拍摄图集的二值化处理，并对每一级的图片进行黑为0和白为1的判定，对黑白分界处存在相位跳变等相位误差进行中值滤波消除，按照对应投射图案的先后顺序组合得到格雷码，并转换为二进制数，再转换为十进制数K值，每个像素对应一个K值，代入式(9)得到相位值φ(x,y)。再通过相位值和投影仪与相机的位置关系运用三角法进行点云重建。

φ(x,y)=φ(x,y)+2π·K

(9)

2 试验与分析

为了验证本文算法检测高反射率表面的有效性，对高反光铝合金表面(如图3所示)进行检测试验。试验中投影仪采用DLP 3010型光机，相机为海康MV-CA050-20UM型号相机，相机分辨率为2 592 像素×2 048像素，帧率为60帧/s。相机距投影仪光轴约为60 mm,相机光轴与投影仪光轴的角度约为15°,工作距离约为240 mm。设置投影仪和相机的曝光时间为5 000 μs，条纹周期为21，通过DLP投影仪烧录格雷码图和相移图，再利用标定板完成相机和投影仪的标定，拍摄图像解算相位，结合标定结果完成点云重建。在相同条纹频率、曝光时间和工件位姿等条件下进行试验，采取3组不同的相移步数，在相同相移步数条件下利用动态解相方法的点云重建质量与传统多步相移方法的点云重建质量来进行对比。

图3 高反光金属件Fig.3 High reflective metal parts

解算相位所需图集包括相移图和辅助条纹(格雷码图)，以相移步数10步为例，采集相移图和辅助条纹图如图4所示。其中，解包裹所需的辅助条纹图如图4(c)～(h)所示，解算相位主值所需的相移图如图4(i)～(r)所示。

图4 解相图集Fig.4 Phase resolution picture

采集相移图和辅助条纹图解算相位，结合相机与投影仪的位姿关系完成点云重建，通过拟合生成的工件点云的标准差判断点云重建质量。

5步相移条件下的传统方法与动态解相的结果对比如图5所示。其中：图5(a)为拍摄的高反光工件原图；图5(b)为5步正弦相移条纹图；图5(c)为采用5步相移传统解相方法重建的点云图，由浅蓝-深蓝-绿的顺序依次表示点云重建质量由好到坏，可看出在工件过曝区域点云重建的质量并不理想；图5(d)为采用5步相移传统解相方法拟合的点云平面图；图5(e)为采用5步相移动态解相方法重建的点云图，对比传统方法结果，从直观上来看过曝区域的点云质量区别不大，其他区域的点云质量有所改善；图5(f)为采用5步相移动态解相方法拟合的点云平面图。

图5 5步相移条件下的传统方法与动态解相的结果对比Fig.5 Comparison of the results of the traditional method and the dynamic phase resolution under the condition of 5-step phase shift

10步相移条件下的传统方法与动态解相的结果对比如图6所示。其中：图6(a)为拍摄的高反光工件原图；图6(b)为10步正弦相移条纹图；图6(c)为采用10步相移传统解相方法重建的点云图，较5步相移而言点云质量有了明显的改善；图6(d)为采用10步相移传统解相方法拟合的点云平面图；图6(e)为采用10步相移动态解相方法重建的点云图，对比传统方法结果，从直观上来看在过曝区域的点云由绿色变为了深蓝色，点云质量略有提升；图6(f)为采用10步相移动态解相方法拟合的点云平面图。

图6 10步相移条件下的传统方法与动态解相的结果对比Fig.6 Comparison of the results of the traditional method and the dynamic phase resolution under the condition of 10-step phase shift

15步相移条件下的传统方法与动态解相的结果对比如图7所示。其中：图7(a)为拍摄的高反光工件原图；图7(b)为15步正弦相移条纹图；图7(c)为采用15步相移传统解相方法重建的点云图，较10步相移而言绿色点云区域明显变少；图7(d)为采用15步相移传统解相方法拟合的点云平面图；图7(e)为采用15步相移动态解相方法重建的点云图；图7(f)为采用15步相移动态解相方法拟合的点云平面图。

图7 15步相移条件下的传统方法与动态解相的结果对比Fig.7 Comparison of the results of the traditional method and the dynamic phase resolution under the condition of 15-step phase shift

通过分别拟合传统解相方法和动态解相方法的点云平面，对5步相移、10步相移、15步相移进行求解标准偏差和平均距离来判断点云质量的好坏，平均距离为整个点云集到该拟合平面的距离。不同相移步数下传统解相方法和动态解相方法的平面拟合的标准偏差、平均距离和时间对比如表1所示。由表1可以看出，在相同的相移步数下，采用动态解相方法的点云质量比传统解相方法略有提升,并缩短了测量时间。

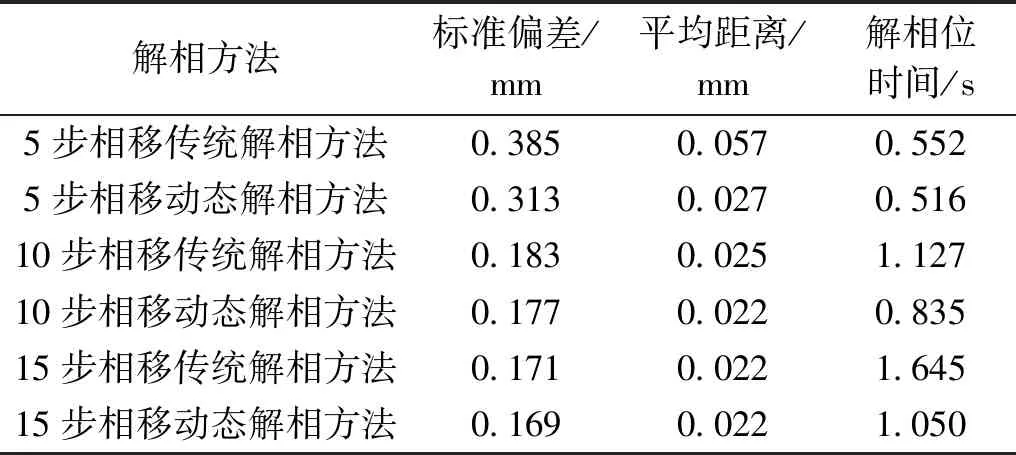
表1 不同相移步数下传统方法和动态解相方法对比

为了进一步评价本文算法，将Li等[11]所提的自适应投影强度调整方法与15步相移动态解相方法所需图像数量、时间以及拟合高反射率物体表面的标准偏差进行对比，结果如表2所示。由表2可以

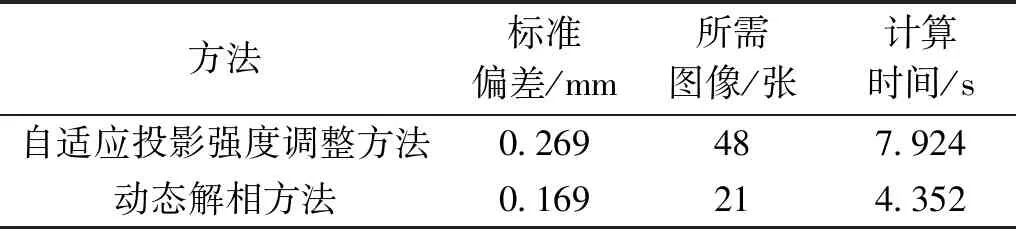
表2 自适应投影强度调整方法与15步相移动态解相方法对比

看出，动态解相方法比自适应投影强度调整方法的点云质量有所改善，但动态解相方法步骤简单，只需拍摄一组解相图集就可完成点云重建,即无需采集多组不同曝光时间图像，所需计算时间较少。

3 结 语

本文针对高反射率表面三维点云测量存在的因像素饱和引入的解相位误差、难以实时测量及实现过程复杂等难题，提出一种基于动态解相的高反射率表面三维测量方法，并在高反射率金属表面进行三维测量。结果表明，该方法只需拍摄一组解相图集即可完成点云重建，且不需要附加硬件设备。在相移步数少的情况下，对高反光区域点云重建的质量并不理想，动态解相时间和传统方法基本一致；当相移步数大于10步时，动态解相方法重建的点云质量略高于传统方法，并有效缩短测量时间。由此表明，本文提出的动态解相三维测量方法能有效测量高反射率表面并且效率更高。