二维变分模态分解在轴承检修中的应用

张惠丽，李嘉楠，石炜，黄迎久

(1.包头职业技术学院电气工程系，内蒙古包头 014010；2.内蒙古科技大学机械工程学院，内蒙古包头 014010；3.内蒙古科技大学工程训练中心，内蒙古包头 014010)

0 前言

列车轴承是保障运输安全的重要部件,轴承故障是威胁列车安全的重要因素之一，为此铁路部门一直对轴承故障的检修十分重视。如图1所示，铁路部门主要通过眼、手和经验判别轴承表面的缺陷程度和缺陷类型，检测结果过于依赖检修人员的经验和责任感，结果并不精确，而且检测结果无法量化，检测数据不能存储和上传，导致检测信息无法利用。轴承内表面的缺陷信息是判断轴承好坏的重要依据。获得高质量图像、更多有效信息的图像，有利于制定检修方案，从而排除安全隐患。

图1 人工检测列车轴承内圈外表面缺陷

变分模态分解(Variational Mode Decomposition,VMD)在2014年由DRAGOMIRETSKIY等正式提出。变分模态分解是自适应信号的分解方法，可将输入信号分解为若干个固有模态函数(Intrinsic Mode Function,IMF)分量。由变分模态分解算法提出了一种自然的二维扩展，即二维变分模态分解(2D-VMD)。该模型可以同时提取多个2D模型并能够寻找各自的中心频率，是一种非递归、完全自适应的变分方法，同时拥有强大的数学理论支撑，能够稀疏地分解图像，参数最小且不需要显式插值就能实现信号的准确分离。因此，本文作者使用模糊线性指数、标准差对IMF分量图像进行客观筛选，剔除无效信息分量后将2D-VMD算法与其他常用去噪算法进行对比；通过均方差和峰值信噪比(Peak Signal-to-Noise Ratio，PSNR)对几种去噪算法进行客观评价。

1 2D-VMD算法的数学模型

为能够更好地应用于图像，将原始VMD模型改造为2D-VMD模型。在二维模型下，不仅能够实现数据保真而且能够最小化组成子信号的带宽，但由于二维信号缺乏一维信号的唯一延伸性，应用单边傅里叶将图像频率移至基带。

由于解析信号频谱具有单边特性，在二维信号中需要将一个半平面的频域设置为0，此分界面向量记为，从而得到2D-VMD在频域中的表达式：

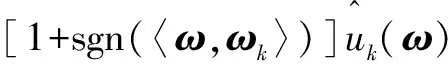
应用傅里叶性质定义二维解析信号:

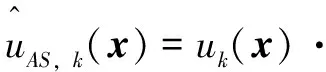
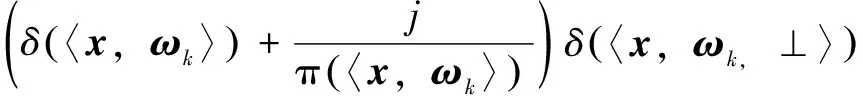
解析信号沿参考方向逐行计算，因此该定义本质上是一维的，但却具有所需求的二维傅里叶特性。

2D-VMD算法是把一个原始信号分解为有限个离散子信号，令原始信号()通过2D-VMD算法进行个分解得到固有模态函数()使得每个IMF都有最小的带宽和，从而得出约束条件下的变分模型表达式：

分解得到个固有模态分量:={，，...，},各分量中心频率：{，，...，}。

为解决重构约束问题，进行算法优化，通过二次惩罚因子，拉格朗日乘子获得交替方向乘法算子(Alternate Direction Met Hod of Multipliers，ADMM)，通过迭代、、，可得到其拓展后的表达式：

({},{},):=

通过上述分析可得数学表示如下：

为解决变分问题,通过迭代，在频域中对其进行傅里叶等距变换：

由于2D-VMD拥有强大的数学理论基础，将信号在频域内对、不断迭代，并更新，当满足迭代停止条件时停止迭代，最后再对其进行傅里叶逆变换，得到最终结果。

2 图像质量评价

主观评价是通过人的自身感官和经验对图像进行判断，人为因素较多，所以主观评价不适于大规模检测。因此，在轴承检测领域更多使用客观评价指标对图像质量进行评价。故引入模糊线性指数、标准差对IMF分量进行客观筛选，选用均方差MSE、峰值信噪比PSNR对去噪算法进行客观评价。

2.1 模糊线性指数

模糊线性指数是反映有效信息量和对比度量值的一种指标，在图像处理中使用比较广泛。经过模糊线性指数验证的图像，值越小图像质量越好，有效信息越明显，越能较好地反映处理前后的变化幅度，其表达式如下：

式中：表示像素点(，)的灰度；表示图像最大灰度；表示图像尺寸。

2.2 标准差

标准差反映各灰度相对于灰度均值的离散情况，是图像对比度的关键量值，在图像处理中同样被广泛应用。值越大图像对比度越高，越能更好地筛选并突出有效信息，其表达式如下：

2.3 均方差

均方差MSE，是图像中各点数据与实际值的偏离程度，两个×的单色图像去噪前、后的灰度(,)、(,)在经过图像处理后的变化程度。去噪后的图像均方差越小，则去噪后的图像质量越好，去噪方法越好。

2.4 峰值信噪比

峰值信噪比PSNR，是最大图像信号与噪声信号的比率，衡量图像在压缩后所呈现的客观品质。目前在世界学术领域内峰值信噪比被广大学者作为常用的客观评价图像质量指标，峰值信噪比越大，图像处理前后的差别越小，失真越少，图像处理后其图像质量越好。

3 2D-VMD算法的去噪原理及参数优化

VMD算法使得一维信号分解为若干个子分量，并对每个分量进行判定，剔除噪声分量，完成一维信号的去噪。2D-VMD是基于VMD的特性扩展而来的，2D-VMD可以实现准确的信号分离，将含有噪声的图像信号分为若干个IMF分量图。采用模糊线性指数和标准差作为IMF的评价指标，分别对每个分量进行筛选，剔除噪声项保留其余含有有效信息的分量，完成二维图像信号的去噪。最后，通过计算MSE和PSNR，对基于2D-VMD的去噪方法进行评价，判定该算法的可行性。2D-VMD去噪原理如图2所示。

图2 2D-VMD去噪原理

2D-VMD算法需要预先设定其中的参数，最主要是分解次数，其次是惩罚参数因子，两个参数的确定对分解过程有着极为重要的作用。在对图像进行处理时，取值过大会导致层数分解过多，丢失大量有效信息，影响重构图像质量；取值过小会使得分离层数少，难以分离噪声和有效信息，达不到良好去噪效果。

2D-VMD对信号进行次分解，产生个IMF分量图，不同的和对分解结果的影响不同。因此，通过粒子群算法对2D-VMD进行参数优化，以避免人为因素干扰，自适应地对合适的参数进行计算，最终选出最优化参数。粒子群算法可以计算每个粒子经过2D-VMD算法处理时，其任意位置所对应的适应度，对粒子位置和移速进行更新，直到循环迭代满足停止条件时停止，最后得出最佳适应度和粒子位置信息。通过粒子群算法对轴承图像进行2D-VMD分解时，当满足=6、=50时有最优参数组合，图像去噪效果最好。

4 实验与结果分析

以Windows10专业版为对操作系统，MATLAB R2015a为仿真软件，研究对象为铁路运输专业轴承(SKF 47N)。

实验选用腐蚀缺陷图像图3(a1)、烧附缺陷图像图3(b1)进行测试。为模拟图像在现实环境中所受到的噪声干扰影响，故对图像添加均值为0、方差为0.04的高斯噪声，缺陷图像分别为图3(a2)、图3(b2)，最后应用2D-VMD算法对缺陷图像进行去噪。

图3 原图和噪声图像

应用2D-VMD算法对含有高斯噪声的两组缺陷图像分别进行分解，令分解层数=6，分别将噪声图像信号分解为6个IMF分量，如图4所示。

图4 2D-VMD分解实验结果

由2D-VMD分解得到的6个IMF分量分别反映了不同层次所对应的原始图像的不同尺度信息，通过观察并对比各分量发现：IMF1包含了原始图像的大部分信息，IMF2、IMF3、IMF4、IMF5为能够表现出原始图像有效信息大致轮廓的趋势分量图，但IMF6则无法看清图中的信息表达，通过主观评价分析IMF6应为噪声项。

应用模糊线性指数和标准差分别对两组实验的6个IMF分量进行客观筛选，腐蚀缺陷组得到的指标为、，烧附缺陷组得到的指标为、。当值较小、值较大时，图像有效信息含量多，图像质量好，最终形成的去噪图像也会呈现出很好的去噪效果。

由表1可知：两组实验的IMF6对应的两项指标都过于异常，模糊线性指数值过大且标准差值过小，证明IMF6图像质量极差，故客观评价IMF6为噪声项。因此，分别去除受噪声影响最大的IMF6，保留其余含有较多有效信息的分量，对其余5个IMF分量图分别进行重构，得到应用2D-VMD算法进行去噪的图像。最后，对含有噪声的图像图3(a2)、图3(b2)进行均值滤波、中值滤波，对比3种去噪算法的去噪效果，结果如图5所示。

表1 6个IMF分量的γ值和σ值

图5 去噪效果对比

针对3种去噪算法，分别计算其对应的评价指标：MSE1、PSNR1、MSE2、PSNR2，对3种算法进行定量分析，客观评价哪种算法去噪效果更好，结果如表2所示。

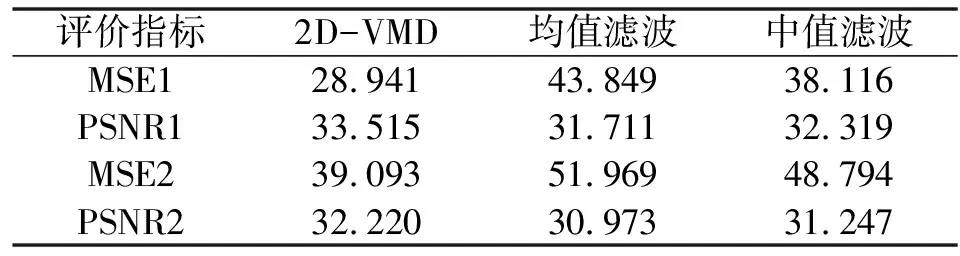
表2 3种算法的MSE和PSNR

通过分析腐蚀缺陷和烧附缺陷去噪实验，可以由MSE1、PSNR1和MSE2、PSNR2直观看出，虽然3种去噪方法都能实现图像的去噪处理，但应用不同的去噪方法得到的去噪图像质量并不相同。通过表2可知：使用2D-VMD得到的去噪图像，均方差最小、峰值信噪比最大，去噪效果最好；中值滤波效果相对较好；均值滤波其均方差最大、峰值信噪比最小，去噪效果最差。由此可知，使用2D-VMD算法进行图像去噪具有较好的去噪效果。

5 结论

本文作者通过分析2D-VMD算法原理，提出基于2D-VMD的列车轴承缺陷图像的去噪方法。将输入的图像信号分成若干个IMF分量，通过粒子群算法对2D-VMD进行参数优化，确定最优参数组合；通过模糊线性指数和标准差两个指标对IMF进行合理客观的筛选，剔除无效信息分量；最后，对其他有效信息分量进行重构，实现对图像信号的去噪处理。通过对比均方差和峰值信噪比，对2D-VMD算法、均值滤波算法和中值滤波算法进行了客观评价，发现使用2D-VMD算法进行图像去噪得到的去噪效果最好、图像质量最清晰、失真最小。研究结果能够为铁路部门的相关故障检修提供参考。