近50年石羊河蔡旗站径流长期演变特征及趋势研究
2022-09-18康建瑛
康建瑛
(甘肃省武威水文站,甘肃 武威 733000)
水资源是人类生产、生活的基础性自然资源,是实现可持续发展的重要基础。甘肃省河西内陆河流域有三大水系,分别是疏勒河、黑河、石羊河,河川径流量主要来自祁连山脉的高山融雪。受干旱气候影响,该地区水资源量极度短缺。研究表明,河西内陆河流域三大水系蕴藏水资源总量约为61.4亿m3,其中疏勒河水系21.2亿m3,占比34.5%;黑河水系23.1亿m3,占比37.6%;石羊河水系17.1亿m3,占比27.9%,石羊河水系水资源量最小。为研究石羊河流域径流的演变趋势及规律,郝强[1]根据石羊河水系各支流1956—2016年的实测径流资料,采用相似年对比法,结合2001年以来景电、西营河调水资料,对蔡旗站2018年的断面来水量进行了分析及预测,为该站在水资源量监测、防汛抗旱方面提供了重要的数据支撑,取得了较好的效果。卢书超等[2]采用MIKE BASIN模型研究了蔡旗断面下泄水量变化特征,认为建立的水资源管理模型是正确的,总体上能反映出蔡旗断面水资源量的变化过程。
为了能够进一步分析蔡旗站降水径流的时序变化特征,使水文监测在水资源监管中更好地发挥作用,本文在上述学者研究的基础上,对蔡旗站的降水、径流量时序变化特征进行研究,可为当地水资源管理提供技术指导与数据支撑。
1 流域概况
石羊河流域是我国河西内陆河流中人口最集中、水资源开发程度最高、用水矛盾最突出的地区之一。石羊河发源于祁连山东端冷龙岭北侧的牛头山,流域面积13.02万km2,出山口以上河长60km,主要支流有西大河、东大河、西营河、黄羊河、金塔河、大靖河、古浪河等,流域内多年平均径流量为15.6亿m3[3]。蔡旗水文站位于石羊河下游,始建于1967年,下游25km处有一座水库,集水面积10209km2。石羊河流域水系及蔡旗站位置见图1。
2 资料与方法
本次研究采用蔡旗站实测长系列逐月、逐年径流资料,分析年际径流变化时,将资料采用线性相关法展延至1956年。经过分析对比,延展方法合理,资料系列经过一致性修正,已经整编为成果资料,可靠度较高,可以使用。采用滑动平均法、Spearman秩次相关法、累积滤波器法对年际径流变化进行趋势分析;采用累积距平法对年径流的丰枯情况及周期变化进行分析;采用有序聚类法、Mann-Kendall检验法检验趋势变化显著性。
2.1 滑动平均法
假设有一水文序列,计算几个前期值和后期值去平均[4],通过计算可以求得一个新的水文序列yt,该方法一般应用在时间序列周期性变化趋势分析中,其结果具有一定的统计性,构造统计量为
(1)
当k=2时,其为5年滑动平均,依次往下计算,但首先要假设原序列具有趋势性,在处理后的yt中能够显示。
2.2 Spearman秩次相关法
Spearman秩次相关法主要是通过分析水文序列Xi及序列i的相关性来检验水文时间序列变化趋势[4],在计算时,时间序列Xi用其秩次Ri代表,可以构造统计量:
(2)
式中:n为时间序列长度;di=Ri-i。如果秩次Ri与时间序列相近,则di较小,秩次相关系数较大,则趋势性显著。
2.3 累积滤波器法
累积滤波器法能够充分显示出时间序列定性的变化趋势,统计量为
(3)
2.4 有序聚类法
有序聚类法是以有序分类来估计序列最有可能存在的突变点,原理为:对于系列Xt(t=1,2,3,…,n)假设具有最优分割点τ,可使同类之间的离差平方和较小,而类与类之间的平方和较大,其计算公式为
(4)
(5)
(6)
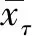
2.5 Mann-Kendall检验法
Mann-Kendall检验法简称M-K检验法[5],是一种非参数统计检验法,也被称为无分布检验,优点在于不需要样本遵从一定的分布规律,也不受异常值的限制,更适用于类型变量及顺序变量,计算也比较简单。主要用于一组序列的变化趋势显著性检验,但前提条件是假设需要检验的序列变化趋势不显著,其计算公式为
(7)
(8)
(9)
(10)
(11)
式中:UFk为检验统计量;Sk为样本统计量;Var(Sk)为Sk的方差。

3 径流长期演变特征及趋势研究
3.1 径流的年内分配特征
胡彩霞等[6]利用基尼系数法对水文年内分配进行了分析,取得了较好的效果,但计算复杂,过程烦琐。本文采用不均匀系数法、完全调节系数法[7-11]对蔡旗站的径流年内分配特征进行研究,其计算过程为
(12)
(13)
(14)
(15)
(16)

经统计,月最大径流量为0.300亿m3,出现在每年的3月,最小值为0.136亿m3,出现在每年的9月;连续4个月径流量最大值为1.115亿m3,出现在1—4月,平均值为0.279亿m3;连续4个月最小值为0.811亿m3,出现在9—12月,平均值为0.203亿m3,连续4个月极值比为1.37,变化基本稳定。点绘逐月径流量年内分布情况,见图2。流量集中期与汛期出现时间相反,主要原因是蔡旗站处于石羊河下游,受上游灌区调水影响。
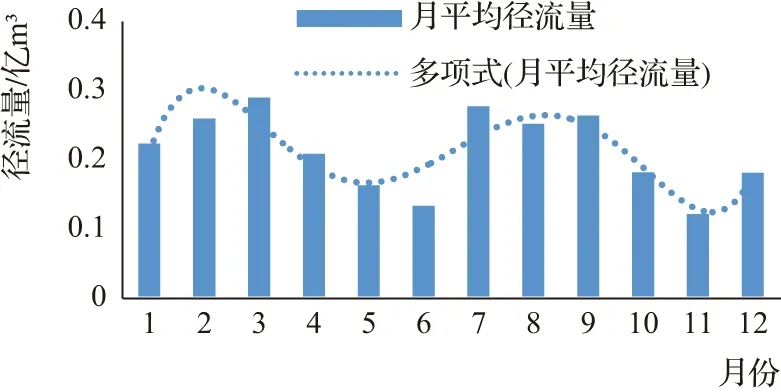
图2 径流量年内分布情况
将蔡旗站的逐月径流量代入式(12)~式(16)中,计算可得该站径流量年内不均匀系数(变差系数),逐月径流量不均匀系数变化曲线见图3。由图3可以看出,不均匀系数最大值为1.54,出现在1988年;最小值为0.29,出现在1985年;多年平均值为0.28;说明1988年径流量的年内分配最不均匀,1985年分配最均匀。计算可得该站逐月完全调节系数Cr值,点绘逐月径流量Cr值变化曲线,见图4,由图4可以看出,Cr最大值为0.419,出现在1988年;最小值为0.002,出现在1989年;多年平均值为0.940。
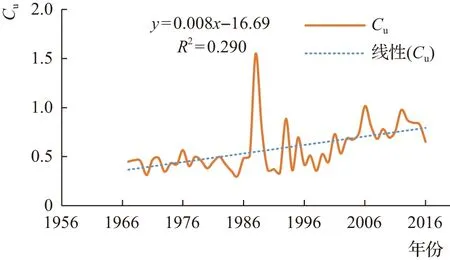
图3 逐月径流量不均匀系数变化曲线

图4 逐月径流量Cr值变化曲线
由图2、图3、图4可以看出,径流量年内分配集中在1—4月、7—9月,进一步证实了上述分析结论;1988年径流量年内分配极不均匀,不均匀系数呈现逐年增大趋势,年内分配逐年不均匀化,但变化不明显;径流量年内分配变得集中,1988年径流最为集中,导致年内分配极不均匀,Cr值出现逐年增大趋势,说明年内分配在逐年集中,进一步验证了径流年内分配不均的结论。造成径流年内分配不均匀的原因主要是大型灌区及水利工程建设导致径流在一定程度上受到影响。
3.2 径流的年际变化特征
径流的年际变化表征水资源量的周期变化,年际径流是水资源量的主要来源。石羊河流域径流量主要靠上游祁连山脉冰雪融水补给。近50年来,该流域共有水资源量176.200亿m3,水资源量比较短缺。经统计,年最大径流量为6.200亿m3,出现在1958年;最小值为0.845亿m3,出现在2002年;多年平均值为2.908亿m3,统计值与《甘肃省第三次水资源评价报告》数据一致。
点绘蔡旗站径流年际变化曲线,见图5。由图5可以看出,该站径流年际变化过程共经历4个阶段:1956—1964年,径流逐年减小;1965—1970年,径流逐年增加;1971—2002年,径流长期处于减小趋势;2003—2016年,径流呈逐年增加趋势;从整体上看,径流量呈逐年减小趋势。牛最荣[3]研究表明,河西内陆河流域径流随流程和年份的增长呈现径流量减小趋势,并计算出了径流定量变化规律,与本次研究结果基本吻合。
图5 蔡旗站径流量年际变化曲线
为了进一步验证该站径流量的演变趋势,采用上述提到的Spearman秩次相关法、累积滤波器法进行趋势分析。经计算,发现两种方法均显示径流呈逐年减小趋势,结果与线性回归法及5年滑动平均法分析一致。采用有序聚类法和Mann-Kendall检验法对径流量序列变化趋势进行显著性及突变检验,变化趋势均表现为不显著。有序聚类法计算显示,|T|=11.9>T0.05/2=1.64,序列在1973年出现显著性跳跃;Mann-Kendall检验法计算的|UF|=2.43>T0.05/2=1.96,突变年份也出现在1973年,且变化显著。点绘两种检验方法的统计曲线,见图6、图7,由图6、图7可以看出,二者检验结果基本一致。

图6 Mann-Kendall检验法趋势检验统计曲线

图7 有序聚类法趋势检验统计曲线
3.3 径流丰枯变化特征
采用累积距平法对蔡旗站径流丰枯情况进行分析,计算其P值(距平百分比),按照径流丰枯划分标准[12]:P>20%,为丰水;10% 本文在收集石羊河蔡旗水文站实测资料的基础上,采用不均匀系数法、线性回归法、滑动平均法、Spearman秩次相关法、累积滤波器法对该站径流量年内分配、年际变化、趋势演变进行了研究;采用有序聚类法、Mann-Kendall检验法对年径流的变化显著性进行了检验。结果表明,径流量年内分配集中在1—4月、7—9月,径流量年内分配逐年不均匀化、逐年集中;径流量整体呈现逐年减少趋势,趋势整体变化不显著,1973年序列出现显著性跳跃;丰枯情况没有很明显的变化特征。受资料系列限制及人类活动影响,本研究稍有欠缺,建议在以后的测验工作中,可将实测来水量进行细致的修正后再进行分析。4 结 语
