基于PSOFS和TSK模糊系统的不平衡心电数据分类算法

李鑫辉，申情，张雄涛

1. 湖州师范学院信息工程学院，浙江 湖州 313000；

2. 浙江省现代农业资源智慧管理与应用研究重点实验室，浙江 湖州 313000；

3. 湖州学院理工学院，浙江 湖州 313000

0 引言

在收集到的心电图数据集中，正常心电图的数量远远多于心律不齐以及心肌梗死的心电图数量，这是典型的不平衡数据[1]。心电图波段繁多、信息繁杂，而且心电图易受各种因素影响，例如过度紧张、发热、躁动等。医学研究者从繁杂的心电图中建立预测规律或者预测模型是极其困难的。而机器学习善于从繁杂数据中挖掘出对应的线性或非线性规律，这能为建立预测模型提供很大帮助。其中，模糊神经网络（fuzzy neural network，FNN）是机器学习中的一个重要领域，其能以规则和模糊集的形式对知识进行表达，因此模糊神经网络具备良好的可解释性。

模糊分类一般包括以下过程：一是模糊划分，将输入样本映射到模糊子空间中；二是建立与子空间相对应的模糊规则；三是借由模糊规则对输入样本进行分类判断。在训练模糊规则时，通常会使用模糊C均值（fuzzy C-means，FCM）算法学习模糊规则的前件。研究表明，FCM算法的集中效果与数据集规模有关，随着数据集规模增大到一定程度，数据规模越增加，集中效果越差。

学者们提出了很多人工神经网络（artificial neural network，ANN）的经典学习算法，例如反向传播（back propagat ion，BP）算法、极限学习机（extreme learning machine，ELM）[2]、径向基函数（radial basis function，RBF）网络[3]等。其中，模糊神经网络是由模糊系统和神经网络构成的网络。然而随着时代的发展，现有的模糊分类器难以满足人们对性能的要求，有学者提出使用集成方法提升模糊分类器的性能。

● Stacking型集成方法：Stacking型集成方法可以多级融合模糊分类器或模糊规则。例如，参考文献[4]训练多个分类器并将其作为初级分类器，再集成初级分类器得到最终集成器；参考文献[5]在模糊规则层面进行集成融合。这种方法的优点是可以提高模糊分类器的分类精度，缺点是集成模糊分类器的初级子分类器不具有可解释性，训练时间较长。

● Boosting型集成方法：Boosting型集成方法的核心在于通过训练得到多个相似却不同的子分类器，典型方法有参考文献[6]介绍的基于AdaBoost的方法，也有参考文献[7]介绍的直接通过修改参数得到不同子分类器的方法。这些方法的缺点在于子分类器之间存在联系，一旦修改就必须重新训练所有子分类器，并且模型的复杂度会变得更高。

● Bagging型集成方法：Bagging型集成方法[8]通过随机放回抽样得到多组子数据集，并用子数据集独立地训练子分类器。这种方法的缺点是其难以准确地处理大规模数据集，且在多数数据集中，Bagging的准确性略低于Boosting。

为了解决上述问题，本文提出基于粒子群优化特征选择（particle swarm optimization feature selection，PSOFS）算法和TSK（Takagi-Sugeno-Kang）的并行集成模糊神经网络（PE-PT-FN）。PE-PT-FN的集成方法是对Bagging型集成方法的改进。PE-PT-FN的贡献如下。

● PE-PT-FN通过对不同标签集分别进行随机放回抽样后再合并获得子训练集，确保子训练集中各类样本分布平衡，从而提升模型对不平衡数据的处理能力。每个子训练集都是原始数据集中的一部分，能在充分保留子训练集可解释性的前提下，降低子分类器之间的相关性。而且，独立且并行的集成模式也确保了模型在集成层面的可解释性。

● PE-PT-FN能控制子训练集的数量规模。训练前件可以提高FCM的聚类性能，使得前件学习更加精确；训练后件能防止因数据集规模过大产生的过拟合问题。

● PE-PT-FN通过PSOFS算法从子训练集中获得特征子集，能减少冗余数据对模型的干扰，从而有效地提升模型的精度。特征选择得到的特征子集还能为医学研究者总结预测规律提供参考数据。

1 相关工作

1.1 TSK模糊系统

本节简单介绍TSK模糊系统[9-11]的构成，对于经典的TSK模糊神经网络（TSKFNN）而言，模糊规则表示如下：

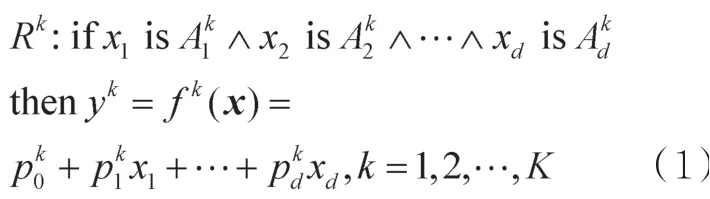
其中，∧表示并且，Rk表示第k条规则，is表示属于，x= [x1,x2,…,xd]表示输入向量，表示第i个输入变量xi对应的第k条规则所描述的模糊子集，K表示模糊规则的数量，是真值参数，yk是按照第k条规则得到的解，f k(x)是yk的函数表达形式。而对于输入向量x而言，y(x)就是yk的加权和：

其中，wk是yk的权值；u k(x)是对应 模糊子集Ak的隶属函 数，可将u k(x)与所有隶属函数的比值之和作为k y的权值，第k条规则的隶属函数如下：代替式（2）中的u k(x)，可得：

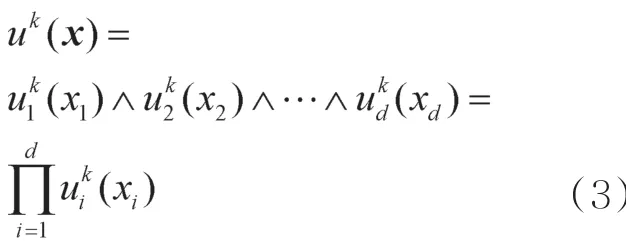
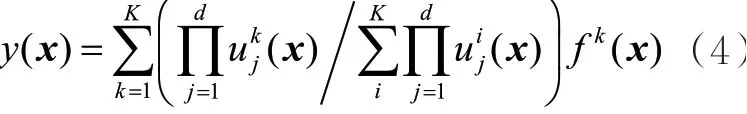
隶属函数有很多种，如三角函数、梯型函数和高斯函数等。式（5）就是高斯函数型的隶属函数。

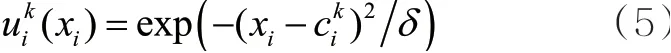
传统的TSK模糊系统难以处理复杂的现实数据，如不平衡数据、大规模数据等。随着社会的发展，人们对模型分类性能的要求逐步提升。为了解决上述问题，本文提出一种基于PSOFS和TSK的并行集成模糊神经网络。该网络能够很好地保留模糊子分类器的可解释性，同时提升对复杂数据的处理能力。

1.2 PSOFS

粒子群优化（p a r t i c l e s w a r m optimization，PSO）算法源于对昆虫、鸟群和鱼群等相互合作的群体集聚行为的思考。这些群体中的成员会根据自己的经验和周围同伴的经验改变自己的搜索策略。PSO算法通过设计一种无质量的粒子群来模拟自然界中的群体，粒子仅具有速度和位置两个属性，速度代表粒子在空间中移动的快慢和方向，位置代表粒子在空间中的坐标。每个粒子都在搜索空间中单独地搜索最优解，并将其记为自身最优位置。粒子群中的所有粒子都会共享自身最优位置，在所有的自身最优位置中挑选出最好的位置作为粒子群全局最优位置。随后，每个粒子都会根据当前自身最优位置和当前全局最优位置来调整自己的速度和位置。

特征选择[12-14]是为了从数据集中选择出效果更好的特征子集。当前的特征选择算法主要分为3种。

● 过滤法：过滤法基于特征的通用表现来选择特征。

● 包裹法：包裹法将结果性能作为特征子集的评价准则。

● 嵌入法：嵌入法将特征选择嵌入训练过程。

PSOFS算法属于典型的包裹法，将结果性能作为特征子集的评价标准。PSOFS算法将数据集的特征空间作为搜索空间，其搜索最佳的特征子集与PSO算法在搜索空间中搜索最佳位置相对应。PSOFS算法使用搜索到的当前特征子集训练学习器，其通过结果性能评估特征子集与PSO算法评估位置相对应。

2 并行集成模糊神经网络

2.1 并行集成模糊神经网络

并行集成模糊神经网络的模型架构如图1所示。DTR和DTE分别表示训练集和测试集，将DTR根据不同标签分成多个不同的标签集。S1,S2,…,SL是L组独立的子数据集。子分类器是相互独立的模糊系统，通过FCM求解前件参数，通过RBF求解后件参数。

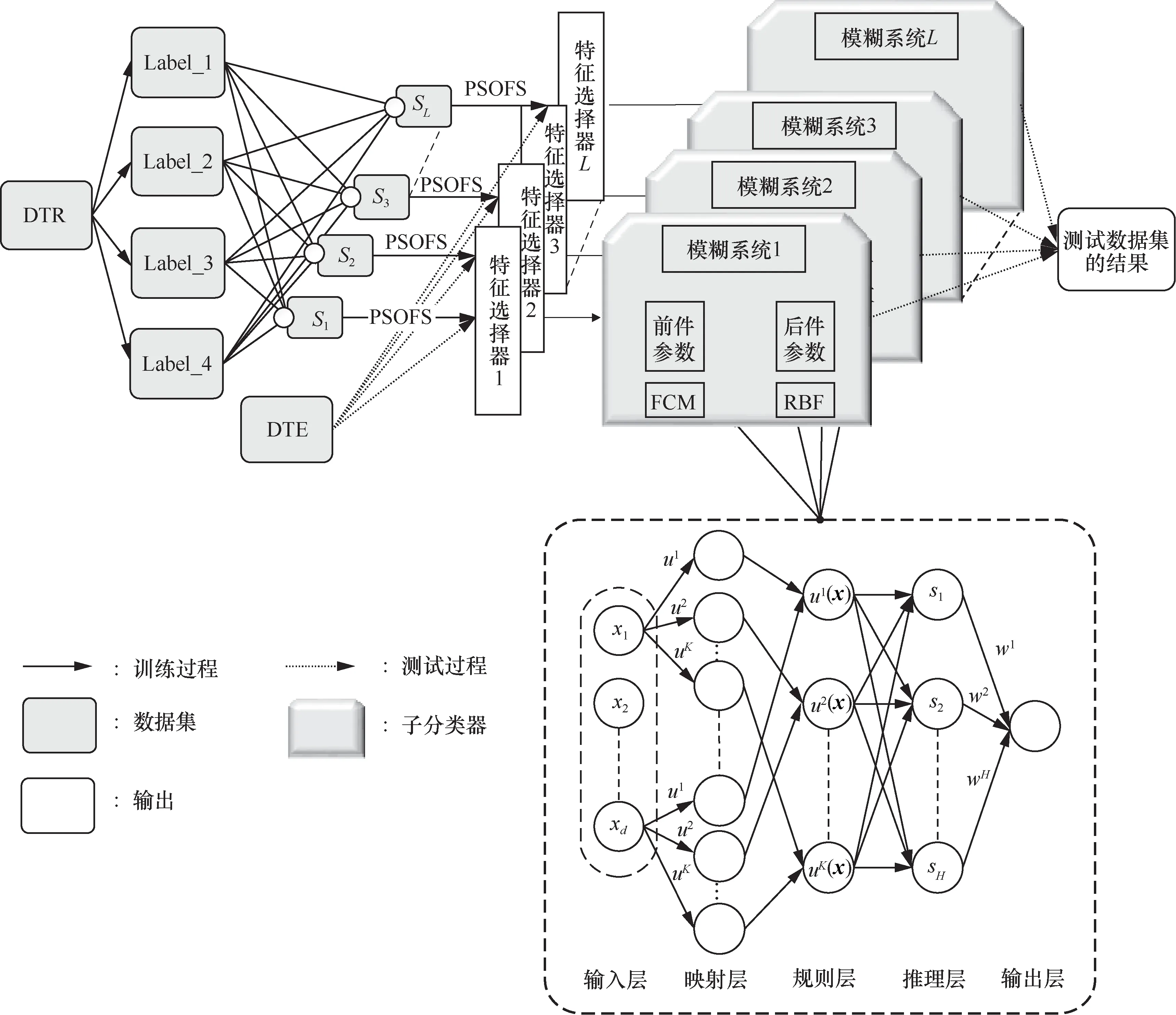
图1 并行集成模糊神经网络的模型结构

训练阶段：为了解决各类标签样本数量不平衡的问题，综合考虑整体样本数量之后，以1 0 0 0为基准从不同标签集中抽取样本。为了尽可能保留训练集的原始特征，子训练集会根据目标标签集的样本量对抽取样本量进行调整并后得到子数据集Si。其中number_Lable_i是当前标签集的样本量，min_number是所有标签集中的最小样本量。每个Si都会通过PSOFS算法搜索得到对应的特征选择器。L组特征子集对不同特征的选用次数表示不同特征的重要程度。每个特征子集都独立地训练出对应的模糊子分类器TSK-FN。在训练TSK-FN时，通过FCM算法学习模糊规则的前件，通过RBF学习模糊规则的后件。与传统的集成学习不同，所有TSK-FN之间都是独立的，可以并行地训练模糊子分类器。这样的并行结构可以独立地对子分类器进行操作而不影响整个集成分类器的效果，后期维护也更加简单。子分类器的实现方法属于神经网络，在本质上属于TSK模糊系统，因此其既有强大的自学习能力，也有可解释性。

测试阶段：测试样本首先通过特征选择器得到特征样本，再通过对应的子分类器得出标签结果，对所有标签结果求算数平均数，取整后作为输出标签。

正则化RBF会将训练集中的所有样本都作为隐藏层节点，拥有部分可解释性和不错的结果。但随着训练集数据量的增加，隐藏层节点数量也增加，时间和空间要求呈指数级上升，且易产生过拟合现象，导致结果精度下降。为了解决上述问题，本文通过对数据集进行随机放回抽样获得多个独立的子数据集，将子数据集规模控制在训练效果较好并且训练的空间成本和时间成本较低的范畴内，使得整个集成分类器能够得到较好的精度，同时降低训练的空间成本和时间成本。子数据集被作为真实数据集的一部分，这为模型带来以下3个好处：

● 提高模型的泛化性，使用不同样本训练得到的子分类器之间的差异性会更大；

● 有利于处理不平衡数据，提高少数类别标签样本的使用率；

● 放回抽样保证子分类器之间有一定的相关性。

2.2 TSK模糊神经网络模型

本节介绍TSK模糊神经网络[15-17]的网络结构，这个网络架构就是图1中模糊系统的模型结构。图2中TSK-FN的第一层到第五层分别是输入层、映射层、规则层、推理层、输出层。其中前3层体现了前件学习。x1,x2,…,xd作为一组d维的输入，通过高斯隶属函数ui获得隶属度u1(x) ,u2(x) ,…,uk(x)，w1,w2,…,wH是正则化RBF隐藏层的权值，也是TSK模糊神经网络需要求解的后件参数，H表示隐藏层的节点个数。

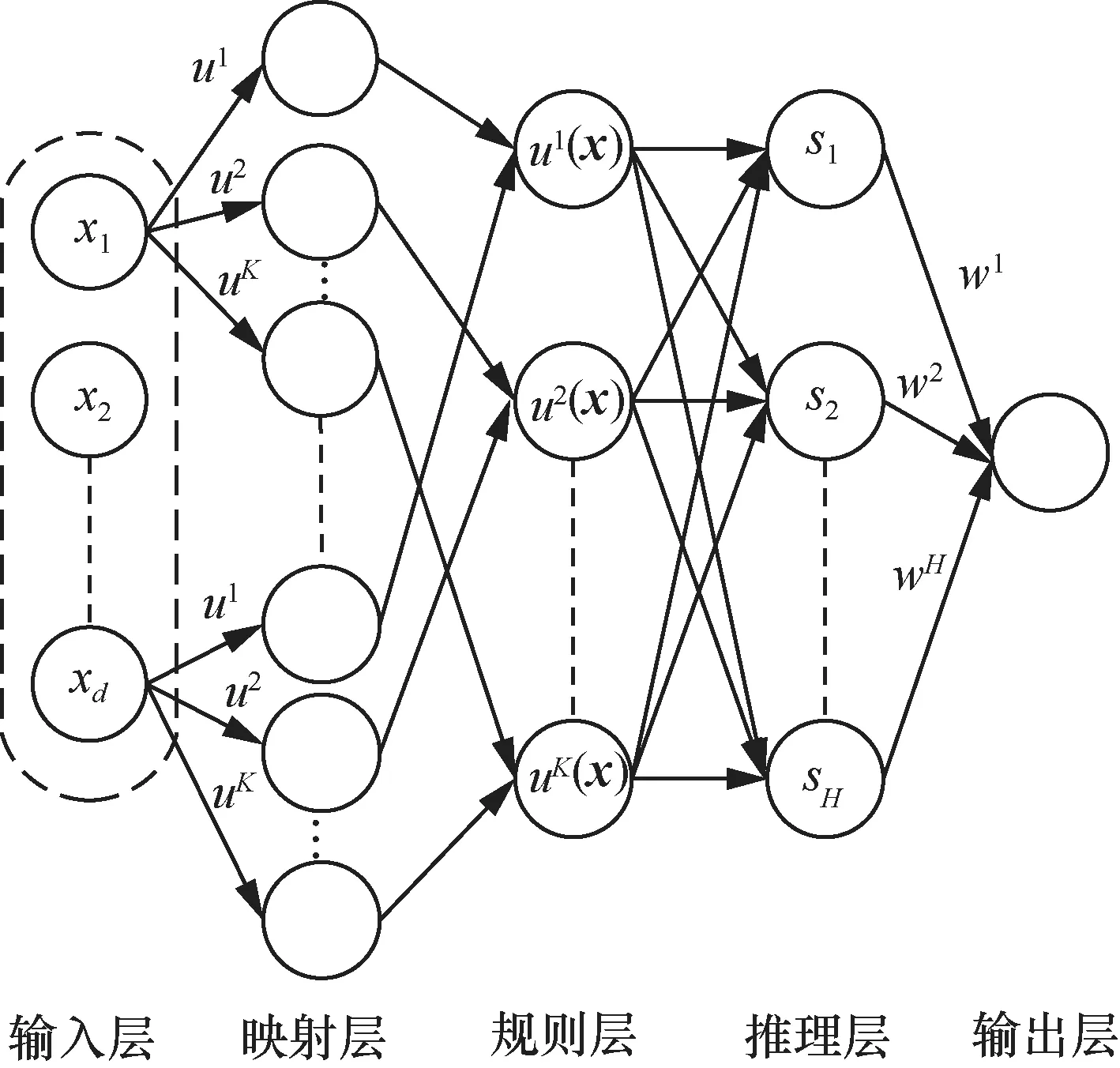
图2 TSK模糊神经网络的模型结构

本文采用的算法是参考文献[18]介绍的FCM模糊聚类算法，以迭代的方式找出最佳的模糊聚类中心，将相应样本的隶属度与该样本到各个类中心的距离乘积之和作为目标参数J。设训练数据集为，，H表示隐藏层的节点个数。

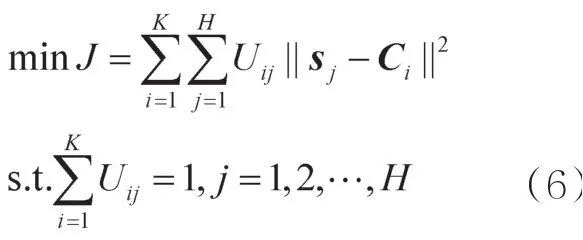
隶属度矩阵U的迭代计算式为：

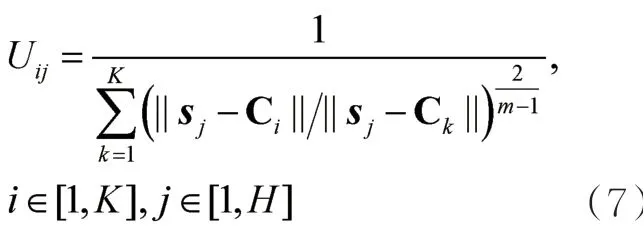
模糊类中心矩阵C的迭代计算式为：

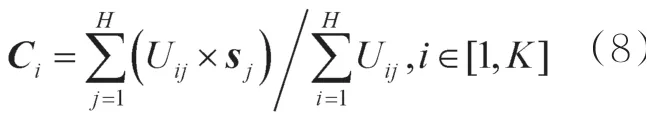
先随机给定一个U，U和C之间能通过式（7）和式（8）获得新的矩阵，反复迭代至收敛。

后两层中的模糊推理和反模糊化输出主要由RBF通过自学习的方法从训练数据集中自行学习得到。将最小均方（least mean square，LMS）规则作为获得模糊后件参数的标准。

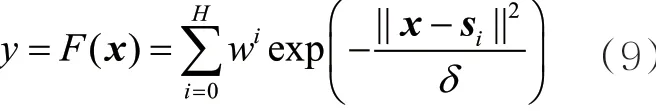
其中，si表示隐藏层节点，在正则化RBF中，每个隐藏层节点对应一组训练数据，iw就是隐藏层节点的权值，求最小均方误差E：

用最小梯度算法就可以求得最小E，对应的w1,w2,…,wH就是隐藏层的权值，也就是模糊后件 的参数。

TSK-FN使用FCM模糊聚类算法求得相应的隶属函数参数，隶属函数参数包含在模糊映射层中。隶属度通过高斯隶属函数模糊化输入数据得到。从规则层到输出层可以被视为一个RBF，其中将规则层作为RBF的输入层，将推理层作为RBF的隐藏层，将输出层作为RBF的输出层。TSKFN上的参数都具有一定程度的可解释性，在医疗研究领域能起到一定的辅助作用。

2.3 PE-PT-FN实现算法

算法1中给出了PSOFS的实现过程。PSOFS算法能在特征维度对应的D维搜索空间中寻找大量的潜在解，在每一代的演化中都会保留历史最优位置best，包括所有粒子的自身最优位置Pi、当前位置sitei和速度Vi。而在下一代的演化中，粒子的信息被用于计算新的速度和位置。其中fit函数表示对位置的评估，位置信息表示特征是否被选用，用被选上的特征训练分类器。将分类器的测试精度作为评估标准。

算法1PSOFS算法

输入：数据集S

输出：特征子集

PE-PT-FN的实现算法可以分为3个过程：一是预处理过程，包括划分子集和选取特征子集；二是训练过程，包括获取模糊前件参数和模糊后件参数；三是测试过程，使用测试集对模型进行评估。

算法2PE-PT-FN算法

输入：数据集data

输出：标签

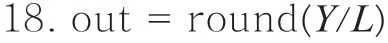
算法2中，PSOFS函数表示算法1描述的粒子群优化算法，Neti表示训练得到的子模糊神经网络，sim函数将测试集通过模型得到预测结果，round函数对结果进行求整，并将其作为标签输出。PE-PTFN算法流程如图3所示。

图3 PE-PT-FN算法流程

PE-P T-F N的空间复杂度体现在隐藏层节点和记录权值的矩阵所需的空间上。例如，n行m列的数据集需要的空间为隐藏层节点个数加上记录权值，即m×n+n×m×n，由此可以 推 断出，空间复杂度为O(n2)。在PE-PT-FN中，空间复杂度为O(n)。分析如下，假设子数据集的规模在9 000左右，每个子分类器的空间复杂度都是O(n2)，分类器个数接近n/9 000，因此整个PE-PT-FN的空间消耗为9 0002×n/9 000=9 000×n。由此可知，PE-PT-FN的空间复杂度是O(n)。

PE-PT-FN的时间复杂度主要体现在计算隐藏层节点的权值和PSOFS迭代所需的时间上。获取隐藏层节点的权值会产生大量的内积计算，RBF的时间复杂度为O(n2)，与上述空间复杂度同理，计算得出训练时间复杂度也是O(n)。PSOFS所需的时间主要消耗在迭代过程中，与数据量大小的相关性很低，单次特征选择的时间复杂度可以被认为是常数量T。假设子数据集的规模在9 000左右，PSOFS的时间消耗为T×n/9 000，时间复杂度为O(n)。由此可知，PE-PT-FN的时间复杂度为O(n)。

综上所述，可以得出结论：PE-PT-FN的空间复杂度和时间复杂度都是O(n)。

3 实验

3.1 实验环境

在硬件平台为Intel Core i5-9400 C×6 CPU，主频为2.90 GHz，内存为8 GB，且编程环境为MATLAB R2018a的系统上进行实验。

3.2 实验数据和设置

实验采用的数据集为阿里云天池大数据竞赛中的训练数据集。该数据集的总样本量为10万份，每列心电信号对应不同类别的病例，分别为正常、心律过快、心率过慢和心肌梗死。对每个心电图样本的信号序列进行频次一致、长度相等的采样，得到1列205维的心电信号序列数据和1维标签数据。实验目标是预测心电图心电信号类别。数据集作为公开数据集，可以从阿里云天池官网中获得。

表1给出了不同模型的参数设置，其中r表示模糊聚类的尺度参数，C表示模糊聚类的聚类中心个数，δ表示高斯核函数的带宽，penalty parameter表示惩罚参数，hidden layer表示隐藏层参数的个数，“—”表示不需要设置该参数。PE-PT-FN有r、C、δ这3个参数需要设置；RBF需要设置δ；ELM需要设置隐藏层参数的个数；ANFIS[19]是将模糊逻辑和神经元网络有机结合的自适应模糊推理系统；参考文献[20]提出用于处理不平衡数据的最近邻插值法GFRNN（gravitational fixed radius nearest neighbor），该方法不需要设置参数；参考文献[21]提出用于处理不平衡数据的少数类合成过采样技术（sy nthetic minority oversampling technique，SMOTE），SMOTE+SVM中高斯核函数的带宽设为1，惩罚参数设为1 000，SMOTE取5个近邻样本。

表1 不同模型的参数设置

3.3 实验结果与分析

本节给出模型从不同标签集中抽取不同数量样例下的实验结果、心电数据集在不同模型中的实验结果以及通过PSOFS得到的特征子集。使用宏准确率（macro-P）、宏召回率（macro-R）和宏F1分数（macro-F1）3种不同的衡量指标来分析评估实验模型。

准确率（P）和召回率（R）是二分类模型的性能度量，准确率的含义是在所有预测正例中真正例的比例；宏准确率是指在执行多分类任务时，两种类别的每个组合都计算一遍准确率，再计算所有准确率的平均值，计算式如下：

召回率的含义是真实情况下所有正例被识别为正例的比例；宏召回率是指在执行多分类任务时，两种类别的每个组合都计算一遍召回率，再计算所有召回率的平均值，计算式如下：

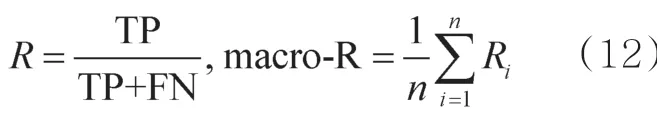
macro-F1是分类问题的平均衡量指标，是macro-P和macro-R之间的调和平均数，计算式如下：

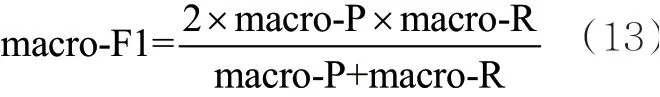
如图4所示，每个子数据集对标签集的取样规模不同，呈现出的实验结果也不同。图4（a）中对每个标签集都取1 0 0 0，图4（b）中对每个标签集都取，图4（c）中对 每 个 标 签 集 都 取。横坐标表示训练时的参数δ，即训练子分类器的高斯核函数的宽度（δ的范围为[0,5]，变化频率为0.1），纵坐标分别表示3种衡量指标。由图4可以直观地发现，通过控制不同标签的数量比例可以有效地改变模型的macro-P和macro-R。引入number_Lable_i来调整从目标标签集中抽取样本的数量，改变子数据集中不同标签样本的比例，从而在一定程度上提升了性能。综合分析可知，子集规模约为9 000时，3种衡量指标效果都较好。当子集规模约为9 000时，与其他模型进行比较，具体见表2。

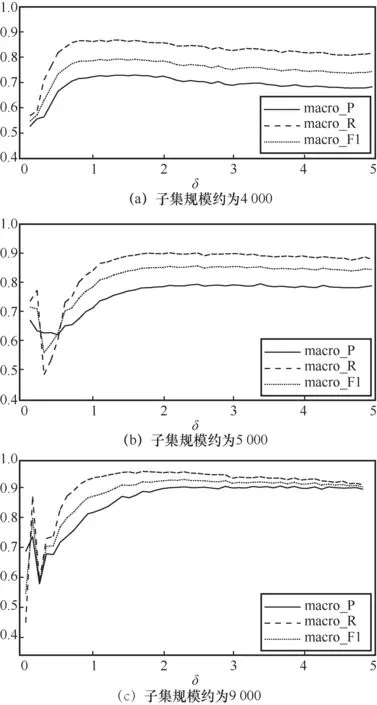
图4 不同规模的子集在不同δ下的实验结果

RBF的实现过程在引言和第2.2节已经有所描述。ELM实现过程的要点在于用给定的输入、输出及随机的输入权重，以求解广义逆的方式得到输出权重。ANFIS在模糊控制的模糊化、模糊推理和反模糊化3个基本过程中使用神经网络的学习机制自动地从输入输出样本数据中抽取规则，构成自适应神经模糊控制器。GFRNN首先在固定半径最近邻规则下从训练集中生成选取模式并将其作为候选，然后根据万有引力定律引入度量值来度量查询模式与每个候选模式之间的距离，最后根据候选对象对查询模式的所有引力之和进行决策。SMOTE的核心在于特征空间上邻近的点的特征都是相似的，因此SMOTE在特征空间中搜寻每个样本点的多个最近邻样本点，随机选择部分邻近点进行差值处理，乘上一个[0,1]的阈值，从而达到随机合成数据的目的。分析表2中的macro-P和macro-R可以发现，RBF、ELM和ANFIS的macro-R均低于macro-P，其中ELM的macro-P与macro-R的差值接近0.1，是3种模型中差值最大的。究其原因，一般的经典算法在面对不平衡数据时，往往会因为考虑精度而以多数类样本为主导，忽略少数类样本，导致macro-R低于macro-P。 PE-PTFN、GFRNN和SMOTE的macro-R均高于macro-P，其中GFRNN的macro-P与macro-R的差值接近0.33，是3种模型中差值最大的。GFRNN会舍弃较多的多数类样本，导致其macro-P远低于其他两种模型。macro-P上表现最佳的是ELM，macro-R上表现最佳的是PE-PT-FN。分析表2中的macro-F1，PE-PT-FN的性能要高于其他对比模型，这表明PE-PT-FN能在保证较好的macro-P的前提下，更好地提升macro-R。综合分析表2能够得到如下结论，PE-PT-FN能够有效地处理不平衡的心电信号数据，并且能够得到较好的结果，在现实中拥有较强的应用性，即PE-PTFN能够更加准确地分析繁杂的心电图数据，从中建立预测模型。

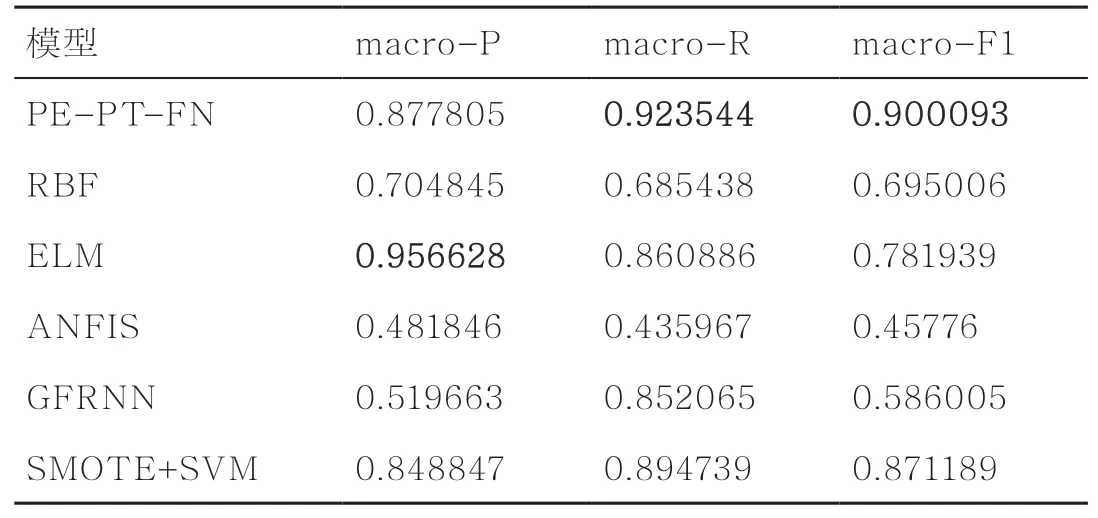
表2 子集规模约为9 000时不同模型的实验结果

使用上述3种衡量指标对不同模型进行评估。从图5可以更加直观地发现，PEPT-FN的 macro-P并不是所有模型中最高的，但在macro-R和 macro-F1上，PEPT-FN要略高于其他模型。RBF、ELM和ANFIS都是macro-P高于macro-R，这主要是受到不平衡数据的影响。GFRNN的macro-R相对较高，但在macro-P上表现相对较差。SMOTE+SVM的表现证明了SMOTE算法能有效地处理数据不平衡问题。PE-PT-FN在macro-P上低于ELM，但在macro-R上均高于其他模型，在macro-F1上也要高于其他模型。综上所述，PE-PT-FN能够很好地处理不平衡心电信号数据的分类问题。

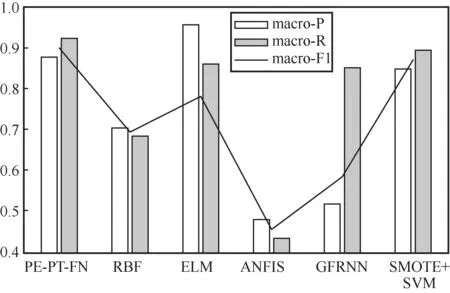
图5 6种模型在3种衡量指标下的表现

实验中设置子集数量为1 4个，通过P S O F S算法对上述3种不同取样策略得到的3组不同的子集进行特征选择。在图4（a）的情况下，通过P S O F S算法得到的特征子集维数分别为(57,52,50,87,70,100,57,69,52,80,40,41,58,58)；在图4（b）的情况下，通过P S O F S算法得到的特征子集维数分别为(47,81,39,67,27,30,60,39, 52,43,50,36,16,67)；在图4（c）的情况下，通过PSOFS算法得到的特征子集维数分别为(68,2 3,18,78,57,5 6,9 0,4 0,3 2,47,27,50,44,39)。对特征选择的结果进行统计，如图6所示。特征维数的被选中次数在一定程度上可以表示该特征维的重要程度，可以为医学研究者的研究工作提供更直观的分析数据。

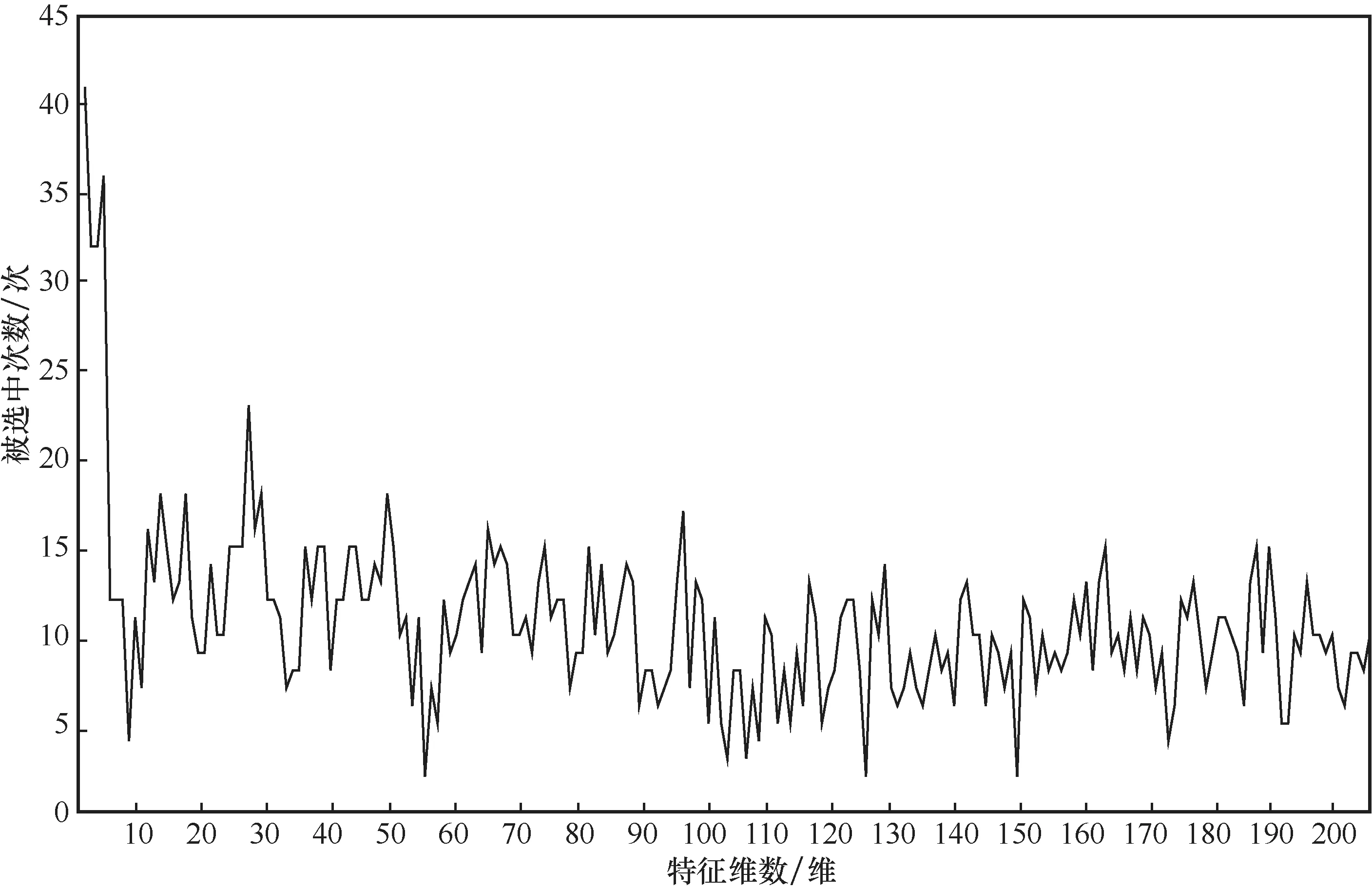
图6 PE-PT-FN实验中不同特征维选中次数统计

4 结束语

本文提出的PE-PT-FN模型在理论部分属于集成TSK模糊系统，具有良好的可解释性；在实现方法部分属于神经网络，具有强大的自学习能力。基于Bagging的集成形式确保了PE-PT-FN模型的稳定性。子分类器之间的独立性确保了PEPT-FN在后期维护中具有良好的操作性。实验证明，PE-PT-FN能够很好地处理不平衡心电数据。同时在训练PE-PT-FN模型时，通过PSOFS算法得到的特征子集、模糊系统中的参数和各个子分类器的结果都能为医学工作者的研究提供分析数据，用于分析心电图与不同疾病之间的关系。

PE-PT-FN模型的训练耗时相对较长，且模糊系统中的参数无法与现实世界对应，仍需研究如何将其转换成对应现实世界的直观知识。为了提高模型的实用性和可信度，未来仍需提高模型的训练速度和参数的可解释性。