一种可重构Stewart型并联机器人的静刚度分析

仇 鑫,尤晶晶,2,叶鹏达,王林康

(1.南京林业大学机械电子工程学院,江苏 南京 210037) (2.南京航空航天大学江苏省精密与微细制造技术重点实验室,江苏 南京 210016)

1965年,英国工程师Stewart在进行飞行模拟器的研究中首次提出一种含6条相同支链的机构,学者们称其为并联机器人[1]. 相比于串联机器人,并联机器人具有结构稳定、承载能力大、累积误差小、动态特性好等特点[2-3],广泛应用于飞行模拟器[4]、医疗机械[5]、六维加速度传感器[6]、人工智能[7]等领域,成为了国内外热门的研究课题. 静刚度是并联机器人一项重要的性能评价指标,直接影响机构的稳定性、承载能力和定位精度. 静刚度不足,往往会使机构产生变形、工作不稳定、定位精度差,甚至会导致机构本身结构的严重破坏. 因此,对于并联机器人的静刚度研究具有非常重要的意义[8].

Gosselin[9]在只考虑主动关节弹性变形的前提下,采用虚功原理建立了空间机构操作力与末端变形间的映射模型. Deblaise等[10]运用矩阵位移法,建立了Delta并联机构的刚度模型. Khasawneh等[11]基于奇异值理论探讨了给定末端位姿后沿任意方向的刚度及其极值间的比例关系,并借助有限元法解算出若干典型构型的末端刚度. 汪满新等[12]以3-RRS并联机构为研究对象,建立了考虑所有运动部件重力及构件/铰链弹性的半解析静刚度模型. 朱伟等[13]研究了一种平面张拉整体机构,基于能量公式对机构刚度进行了分析,并得到了机构在平衡状态下的刚度分布等高线图. 张东胜等[14]针对2RPU/UPR+RP五自由度混联机器人,分别求解并联部分与串联部分两子系统的静刚度模型,从构造系统的力旋量系和弹性变形协调条件入手,结合变形叠加原理与串联部分微变形,建立了混联机器人的整体刚度模型.

然而,现有的研究主要聚焦于少自由度并联机构的静刚度,对于六自由度并联机构,尤其是六自由度变拓扑驱动型并联机器人的静刚度特性分析相对较少. 该类问题的难点是系统的输入、输出量较多,特别是同时包含了移动和转动,而且,转动又会进一步衍生出新的移动. 本文提出一种新型的含混合单开链支路的Stewart型并联机器人. 首先,为降低机构的耦合度,设计了一种三重复合虎克铰链;为实现变拓扑驱动,设计了一种可以转换主、从运动的移动副;接着,基于速度基点法推导出并联机器人的速度雅可比矩阵,并结合虚功率原理,建立了机器人的静刚度计算模型;最后,运用SolidWorks Simulation静力学仿真软件分析了机器人的刚度特性,进一步验证了理论算法的正确性. 这为并联机器人后续的结构优化以及性能分析研究奠定了理论基础.

1 机构描述

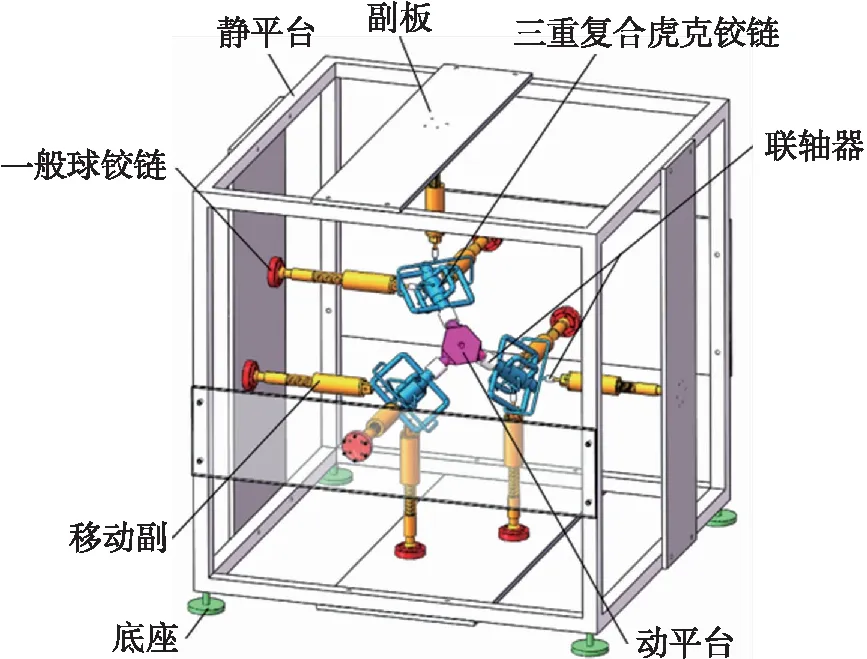
图1 Stewart型并联机器人结构模型Fig.1 Structure model of Stewart parallel robot

图2 Stewart型并联机器人拓扑构型Fig.2 Topological configuration of Stewart parallel robot

图3 三重复合虎克铰链结构模型Fig.3 Structure model of triple compound Hooke hinge

如图3所示,为了降低机构的运动耦合度,设计了一种三重复合虎克铰链[15],其主要由第一层铰链、第二层铰链、第三层铰链和中心柱组成. 第一层铰链由第一套筒、外叉和第一U形过渡段组成,第二层铰链由第二套筒、中叉和第二U形过渡段,第三层铰链由第三套筒和内叉组成. 三层铰链均具有3条互相垂直的转动轴线,并且转动轴线始终相交于点Uj(j=1,2,3).

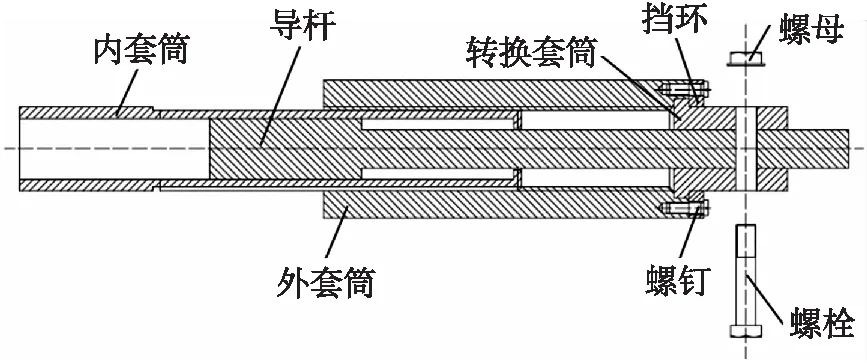
图4 移动副剖面图Fig.4 Profile of prismatic joint

图5 移动副3种工作模式结构简图Fig.5 Structure diagram of three working modes of prismatic joint

如图4所示,为了改变机构的冗余度,设计了一种可转换主、从运动的移动副[16],其主要由导杆、内套筒、外套筒和转换套筒组成. 导杆与内套筒之间滑动连接,内套筒与外套筒之间通过螺纹连接. 当转换套筒与导杆通过螺栓和螺母固定时,旋转外套筒,带动转换套筒和导杆一起移动,此时为主动模式,该工作模式下的移动副又称为驱动副. 当转换套筒与导杆无固定时,外套筒不起作用,导杆在内套筒的筒体内光滑移动,此时为从动模式,该工作模式下的移动副又称为从动副. 当转换套筒与导杆通过螺栓和螺母固定时,外套筒固结于内套筒外表面,套筒和导杆相对静止不动,此时为锁合模式,在该工作模式下移动副等效为刚性杆件. 移动副3种工作模式下的结构简图如图5所示. 当任意选取与自由度相等个数的移动副为驱动副时,机构为一般驱动;当选取大于自由度个数的移动副为驱动副时,机构为冗余驱动. 限于篇幅,锁合模式将另文研究.

基于移动副的工作模式,将Stewart型并联机器人重构为3种拓扑构型,分别是3-3-3构型、3-2-1构型和2-2-2构型(前、中、后3个数字各代表一条混合单开链支路中驱动副的个数),如图6所示. 其中,3-3-3构型为冗余驱动,3-2-1构型和2-2-2构型为一般驱动.

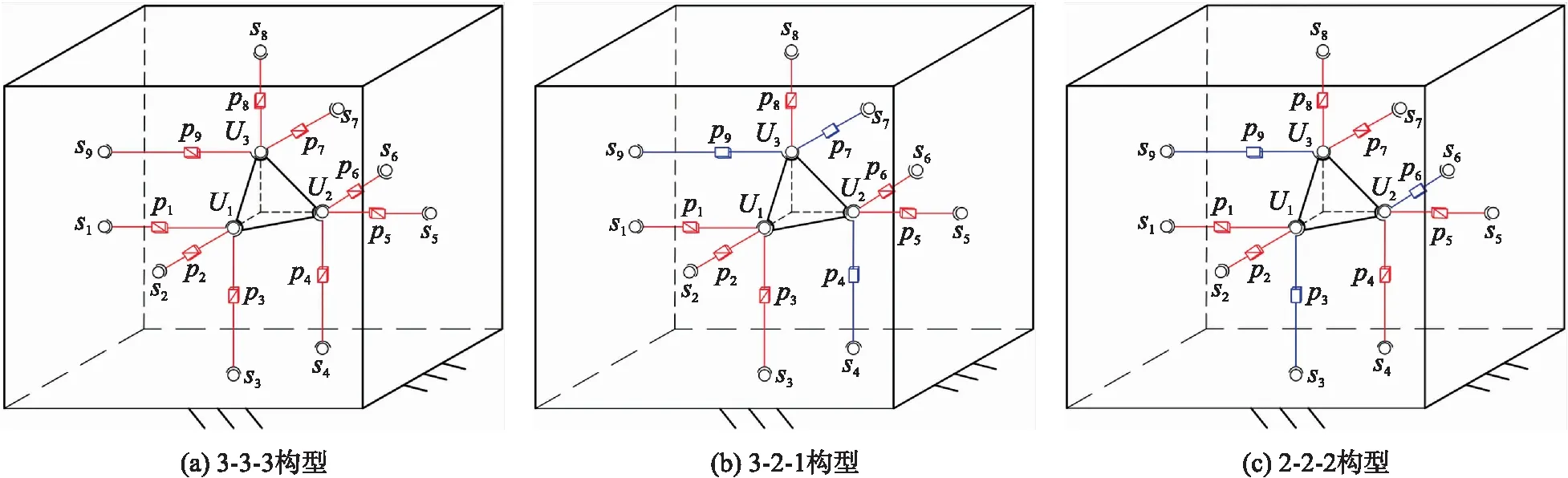
图6 Stewart型并联机器人重构构型Fig.6 Reconfiguration of Stewart parallel robot

2 并联机器人静刚度的数学模型

2.1 速度雅可比矩阵的推导

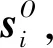
表1 铰链几何中心在静坐标系中的位置矢量Table 1 The position vector of the geometric center of a hinge in a static coordinate system

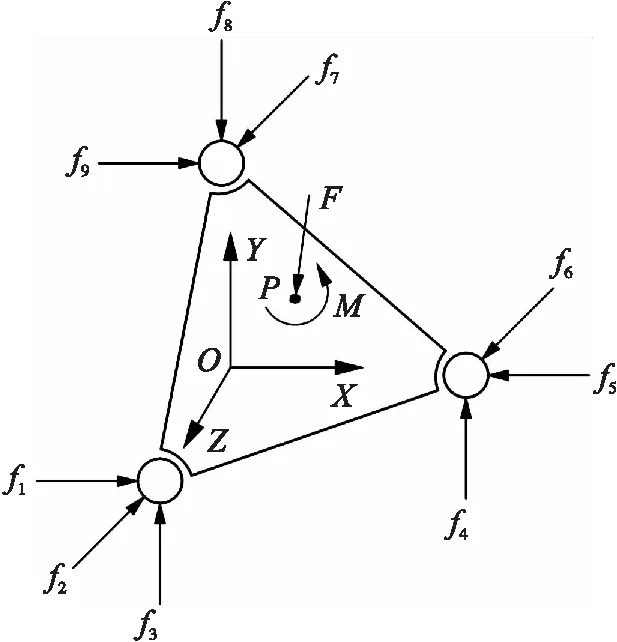
图7 3-3-3构型并联机器人受力分析图Fig.7 Force analysis diagram of 3-3-3 configuration Stewart parallel robot

以3-3-3构型并联机器人为例,当机器人的位形一定时,各支链长度确定,成为一个稳定的机构. 此时在动平台上作用六维力矢,9条支链上会产生反作用力,忽略其自身重力和运动关节处的摩擦力,则这些反作用力是沿支链方向的. 受力分析如图7所示.

在动平台上任选一点P为参考点,基于速度基点法,三重复合虎克铰链的速度可以解析表示为

(1)

式中,vP、ωP分别表示点P的线速度和动平台的角速度,PO表示点P在静坐标系中的位置矢量.

将式(1)等号两端同时点乘支链的单位方向向量,整理后可得第i条支链的速度为

(2)

式中,hi表示支链i的单位方向向量.

(3)

式中,li表示为第i条支链的长度.

将式(2)写成矩阵形式

(4)

(5)

同理,3-2-1构型和2-2-2构型并联机器人的速度雅可比矩阵分别为

(6)

(7)

2.2 静刚度矩阵的推导

基于式(4)及变分原理,可得虚位移方程

δl=JAδX,

(8)

式中,δX=(δxδyδzδαδβδγ)T.

式(8)进行一阶等时变分处理,可得虚速度方程

(9)

通过对式(8)和式(9)的观察后发现,得到两个虚位移矢量和两个虚速度矢量都与机构的速度雅可比矩阵有关.将施加在动平台上的六维力矢简化为一个合力矢量F和一个力偶矢量M,根据虚功率原理,可得

(10)

将式(2)、(4)代入式(10),虚功率原理还可以表示成矩阵形式

(11)

式中,f=(f1,f2,…,f9)T.

将式(9)代入(11),可得

(12)

式(12)对于任意虚速度均成立,因此,施加于动平台上的外力和驱动支链产生的反作用力之间的关系可通过速度雅可比矩阵联系起来

(13)

根据Hooke定律,驱动支链轴向力及其变形之间关系为

f=kAδl,

(14)

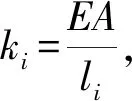
结合式(8)、(13)及(14),可得动平台所受的外力与其产生的微位移的关系为

(15)

假设各支链的等效弹簧系数相同,均为k,以动平台原点M为参考点.初始位姿下,3-3-3构型并联机器人的速度雅可比矩阵和静刚度矩阵分别为

(16)

(17)

同理,3-2-1构型和2-2-2构型并联机器人的速度雅可比矩阵和静刚度矩阵为

(18)

(19)

(20)

(21)

式中,JB、KB分别为3-2-1构型并联机器人的速度雅可比矩阵和静刚度矩阵,JC、KC分别为2-2-2构型并联机器人的速度雅可比矩阵和静刚度矩阵.

3 软件仿真

以3-3-3构型并联机器人为例,在SolidWorks中建立简化的三维模型,其中,将每条驱动副等效为二力杆,三重复合虎克铰链等效为三重复合球铰链,机构的主要结构参数如表2所示.

表2 3-3-3构型并联机器人主要结构参数Table 2 Main structural parameters of 3-3-3 configuration Stewart parallel robot mm

以机构初始位姿为研究对象,借助SolidWorks Simulation静力学仿真软件对其进行仿真. 为简化分析,将静平台、动平台、一般球铰链以及三重复合球铰链等效为刚度无限大的刚体,并根据并联机器人的运动特点及零件的应用场合,驱动副材料设定为45钢,材料属性如表3所示.

表3 材料属性Table 3 Material properties

网格划分是进行静力学分析的关键,划分不合理会导致计算不收敛. 并联机器人整体使用四面体单元进行网格划分,整机共有140 597个单元和267 843个节点,如图8所示.

图8 3-3-3构型并联机器人网格划分模型Fig.8 Meshing model of 3-3-3 configuration Stewart parallel robot

将静平台设定为固定几何体,在动平台原点处同时施加3个作用力,方向分别沿X、Y、Z轴方向,大小分别为100 N,得到机构中零部件的微位移变化云图,结果如图9所示.

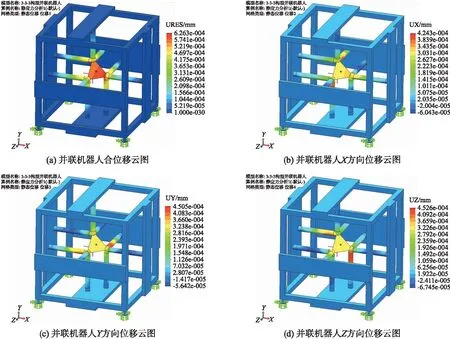
图9 3-3-3构型并联机器人位移云图Fig.9 Displacement cloud of 3-3-3 configuration Stewart parallel robot

对于3-2-1构型和2-2-2构型并联机器人,构型中有3条从动副,由于从动副在机构运动过程中不承受力,因此在简化三维模型中可将从动副删除,其余仿真条件不变. 仿真结果如图10、图11所示.

图10 3-2-1构型并联机器人位移云图Fig.10 Displacement cloud of 3-2-1 configuration Stewart parallel robot

图11 2-2-2构型并联机器人位移云图Fig.11 Displacement cloud of 2-2-2 configuration Stewart parallel robot

通过观察图9、图10、图11可以得出,在初始位姿并施加相同的作用力时,3-3-3构型并联机器人静刚度性能最优,2-2-2构型并联机器人静刚度性能最差;3-3-3构型和2-2-2构型并联机器人在各自的X、Y、Z3个方向上的静刚度性能基本相同;3-2-1构型并联机器人在X、Z方向上的静刚度性能基本相同,在Y方向上的静刚度性能最差. 该结果与各构型并联机器人的结构特征相吻合.

限于篇幅,本文仅对比并分析δX中前3个元素的理论计算值和有限元仿真值. 根据式(15)～(21),求解出并联机器人在3个方向上的位移值. 定义σ为有限元仿真结果与理论计算结果的相对误差,其表达式为

(22)

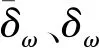
表4 数值计算与有限元仿真结果对比Table 4 Comparison of numerical calculation and finite element simulation results

从表4可以看出,理论计算结果均接近于有限元仿真的结果,相对误差在18.36%以内,参考文献[17-19],该结果在允许的范围内,其主要原因是两者支链的等效弹簧系数ki存在相对误差. 这表明,所建立的Stewart型并联机器人静刚度模型是正确、有效的.

4 结论

(1)提出了一种构型冗余且对称的新型 Stewart型并联机器人,并对并联机器人的结构模型进行了设计. 通过设计三重复合虎克铰链,降低了机构耦合度;通过设计可以转换主、从运动的移动副,实现了变拓扑驱动.

(2)基于移动副的工作模式,将Stewart型并联机器人重构为3种拓扑构型,基于速度基点法推导出3种构型的速度雅可比矩阵,并结合虚功率原理,建立了并联机器人的静刚度模型.

(3)采用SolidWorks Simulation静力学仿真软件对机构静刚度模型进行了分析,结果表明,3-3-3构型并联机器人静刚度性能最优,2-2-2构型并联机器人静刚度性能最差,且两种构型在各自的X、Y、Z3个方向上的静刚度性能基本相同;3-2-1构型并联机器人在Y方向上的静刚度性能与其余两个方向相比较差.

(4)与有限元仿真结果对比发现,所建立的静刚度模型误差在18.36%以内,验证了静刚度模型的合理性和正确性,为Stewart型并联机器人下一步的结构优化和性能分析奠定了基础.