红椿近成熟天然次生林直径分布

钟昌龙, 施维华, 李国秀, 汪洋, 宋菲

红椿近成熟天然次生林直径分布

钟昌龙1, 施维华2, 李国秀1, 汪洋1, 宋菲3, *

1. 湖北生态工程职业技术学院, 武汉 430200 2. 堵河源自然保护区管理局, 湖北竹山 442200 3. 湖北省林业科学研究院, 武汉 430075

红椿; 近成熟天然次生林; 直径分布; 拟合; Weibull函数

0 前言

林分结构是森林生态系统的基本特征, 是森林不同自然生态过程以及人为干扰的结果[1-2]。天然林林分内部的许多特征因子, 如直径、树高、形数、材积和树冠等, 都具有一定的分布状态, 而且表现出较稳定的结构规律性[3], 是决定森林能否充分发挥其功能的前提[4]。林分直径结构反映了林木在各径级的株数分布, 对林木的树高、树干干形、材质与出材率、枝下高和冠幅大小等因子有显著的影响[5-6]。研究林分直径分布有助于诊断森林结构是否稳定, 并解释特定林分的独特生长模式[7], 评价林分效益与功能, 辅助编制各种林分生长过程表和林分出材量表, 以便制定合理的经营方案和有效的森林经营措施[8]。

作为研究林分直径结构的重要方式, 林分直径分布函数研究历来受到国内外学者的关注[9]。利用不同概率分布函数, 如Gamma分布[10-11]、Logistic分布、Normal分布、Lognormal分布和Weibull分布[8, 11-13]拟合林木直径分布是较常见的方法。由于林分直径分布可以综合反映林分发展过程如更新方式、竞争、自稀疏和经历的干扰活动[2], 对于生长发育过程中因某一年龄阶段受到环境筛的过滤而导致濒危的“关键阶段”型濒危植物[14], 是否可以通过直径分布研究, 揭示造成其生态幅狭窄的关键因子, 从而制定物种保护策略, 是具有一定科学意义的。

红椿()是国家二级重点保护植物, 具有重要的经济价值和生态价值。人为的过度开发以及天然更新较慢, 导致其数量不断减少[15]。目前, 红椿研究主要涉及植物生理、生长特性、造林、生态学、优树选择和遗传研究[15-17]。本研究以湖北红椿近成熟天然次生林为研究对象, 选用5个分布模型对红椿直径结构进行模拟分析和检验, 选出最优模型, 并利用最优模型的参数进一步构建预测模型, 以期在生产实践中快速准确预测红椿天然林分直径分布规律, 了解林分结构特征, 合理调节林木直径结构, 使林分中小径级红椿获得足够环境资源, 促进林下小径级红椿林木的正常生长和林下更新, 为红椿资源保护和发挥群落生态功能提供依据。

1 研究区概况

湖北省位于东经108º21′—116º07′, 北纬29º05′—33º20′, 全省地势呈西高东低状, 地貌形态多样化。湖北气候和土壤条件变化丰富, 生境复杂多样。红椿主要分布在鄂西南、鄂西北山区和鄂东南山区或丘陵。红椿分布区森林资源丰富, 主要植被类型为常绿阔叶林、常绿落叶阔叶混交林或针阔混交林。红椿地理信息与立地条件见表1。

2 研究方法

2.1 样地设置与调查

2017年对湖北红椿天然次生林进行调查。选取人为干扰程度相对较轻, 具有代表性的10个红椿近成熟天然次生林。每个样地设置20 m×20 m标准样方。共设置15个样方, 其中10个样方用于直径分布研究, 5个样方(建始、通山、黄石、竹山、谷城各一个)用于检验预测分布模型(见表1)。对样方内乔木进行每木检尺, 林木起测直径(DBH)为2 cm。分别测定林木直径、树高和枝下高, 并记录林下主要灌木和草本(表2)。

2.2 分析方法

2.2.1 峰度和偏度

直径分布的形状可以用偏度与峰度来评价[10-11]。表示非对称的偏斜方向与偏斜程度,>0表示正偏差数值较大, 即均值在峰值的左边, 为左偏;<0表示负偏差数值较大, 即均值在峰值的右边, 为右偏。的绝对值越大则表明偏斜程度愈大。峰度表示分布曲线的尖峭或平坦程度,>0表示尖峭;<0表示曲线较正态分布平坦。

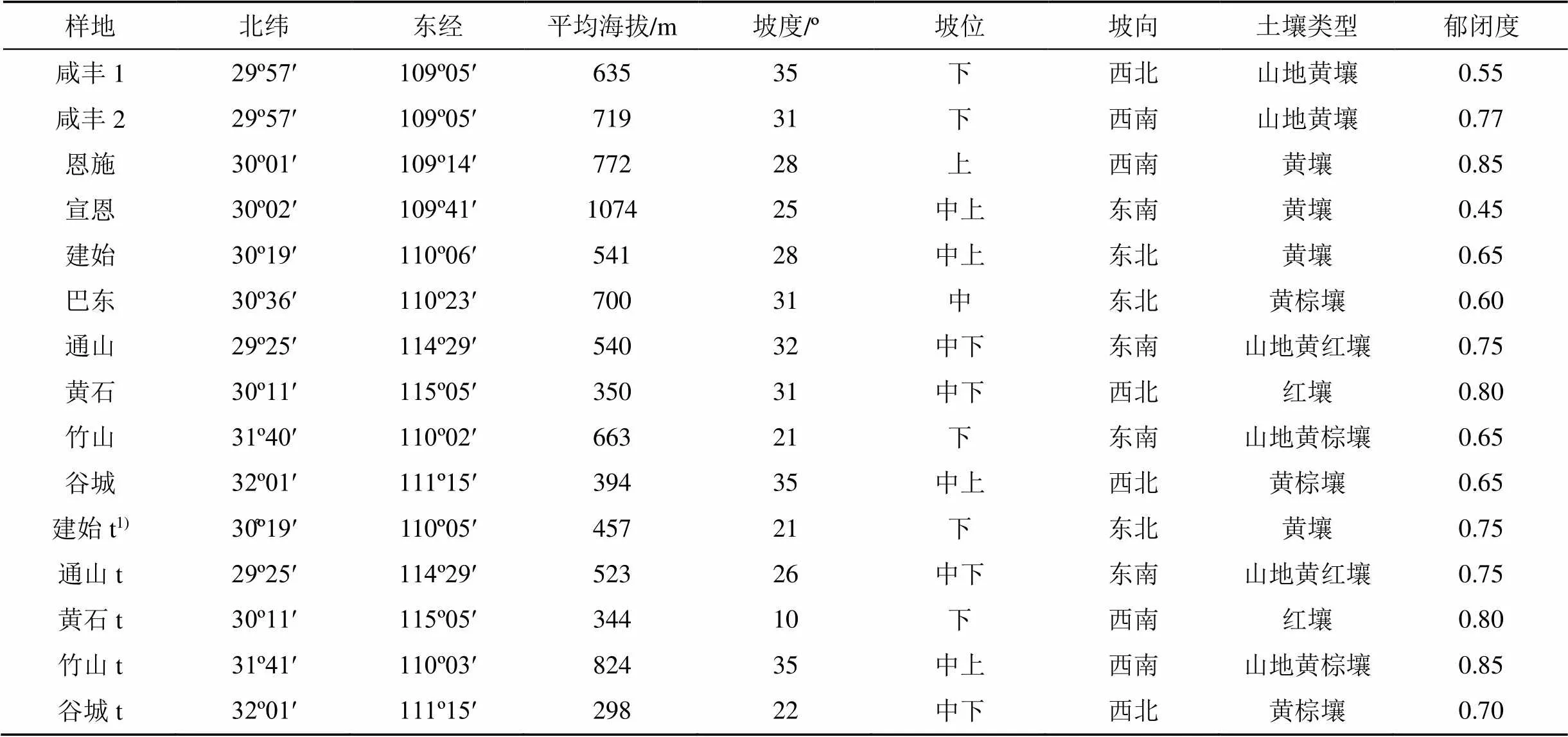
表1 红椿样地地理信息与立地条件

注:1)t.该样地数据用于对预测模型的检验。

表2 红椿样方群丛组成与林分密度

偏度和峰度的计算公式为:

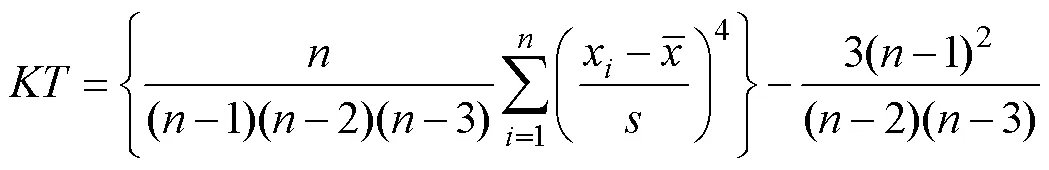
式中为林木株数;x为每木直径; ͞为算术平均直径;为标准差。

变异系数是直径标准差与算术平均直径的比值, 其值越大, 表明直径分布范围越大。

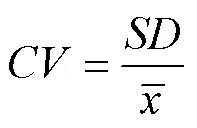
2.2.2 林分直径分布选择模型

利用Gamma分布、logistic分布、normal分布、lognormal分布、Weibull分布分别拟合10个红椿天然次生林林木直径分布。

(1) Gamma分布概率密度函数:

式中:为尺度参数,为形状参数。

(2) Logistic分布概率密度函数:

式中:()为各径阶株数的累计频率;为径阶中值;为累积分布概率为1/2时所对应的林木直径;为尺度参数。

(3) Normal(正态)概率密度函数:

式中:为正态分布的数学期望,为林分直径标准差。决定正态分布的位置,决定正态分布的分散大小。

(4) Lognormal(对数正态)概率密度函数:

式中:为随机变量ln()的平均数,为随机变量ln()的标准差。

Lognormal分布为偏态概率分布, 有的林分直径分布为此形状[18-19]。

(5) Weibull(正态)概率密度函数:

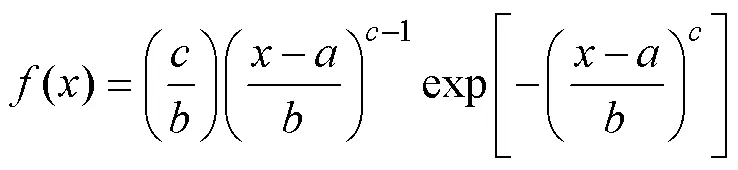
≤≤∞,>0,>0 (8)

式中:为林木实测直径;为位置参数,为尺度参数,为形状参数。

2.2.3 分布模型检验

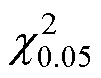
2.2.4 参数预测模型

多因子模型参数采用方差膨胀因子(, variance inflation factor)进行检验。即利用各变量之间存在多重共线性时的方差与不存在多重共线性时的方差比值来进行判断。当0<<10时, 表示参数间不存在多重共线性[10-11,20]。表达式如下:

研究按2 cm标准整化径阶并分级, 数据采用Excel 2013、SPSS 22和ForStat2.1处理。

3 结果与分析

3.1 红椿直径分布特征

直径分布曲线左偏的程度越大, 说明其越偏向中小径阶, 变异系数较大[8]。10个红椿样地的林分直径分布>0, 平均值为0.6081, 曲线均为左偏,大小依次为: 咸丰1>宣恩>建始>咸丰2>黄石>谷城>巴东>竹山>恩施。统计学意义上, 样地直径分布偏斜程度均不大。平均值为-0.4053, 表明大多数样地直径分布曲线比标准正态分布曲线略平坦。咸丰1和宣恩的>0, 直径分布偏尖峰态, 其林分直径分布相对比较集中, 离散程度较大; 其它8个样地的<0, 直径分布偏平坦, 表明不同径阶林木株数在林分中较为均匀, 直径分布离散程度较小。

表3 红椿样地林木统计

3.2 分布拟合与检验

林木直径分布拟合参数见表5。以2检验值(>0.05)为依据, 咸丰1、咸丰2、宣恩、建始和谷城样地的林木直径分布符合Gamma分布, 且1<≤2, 曲线基本为单峰曲线。除黄石外, 全省9个样地林木直径分布符合Logistic分布。Normal函数拟合不能解释10个样地林木直径分布。咸丰1和竹山样地林木直径符合Lognormal分布。除黄石外, 全省9个样地林木直径分布符合Weibull分布。

表4 SK、KT与林木特征因子相关分析

注: **. 0.01显著相关; *. 0.05 显著相关。

10个样地林木的Gamma函数形状参数估计值均大于2, 说明红椿林分林木直径分布曲线是先下凹, 中间上凸, 最后下凹, 其密度函数曲线与图1所显示的结果基本一致。10个样地Weibull分布函数形状参数的估计值均大于1, 且小于 3.6, 林木的直径分布曲线表现为左偏山状, 即反“J”型, 与系数研究的结果相似。

由图1可以看出, 咸丰1、咸丰2、宣恩、建始和谷城样地红椿林木分布观测值与Gamma分布曲线相似。黄石样地林木直径分布观测值与Logistic拟合值相差较大。10个样地Normal分布拟合值与观测值相差很大。仅咸丰1和竹山样地直径分布观测值与Lognormal分布拟合相似。黄石样地林木分布观测值与其Weibull分布拟合值与有较小差异, 其他样地Weibull分布拟合值与样地林木直径分布观测值分布曲线的相似程度较高, 表明Weibull分布函数拟合红椿天然林林木直径分布较为理想。

3.3 参数预测模型与检验

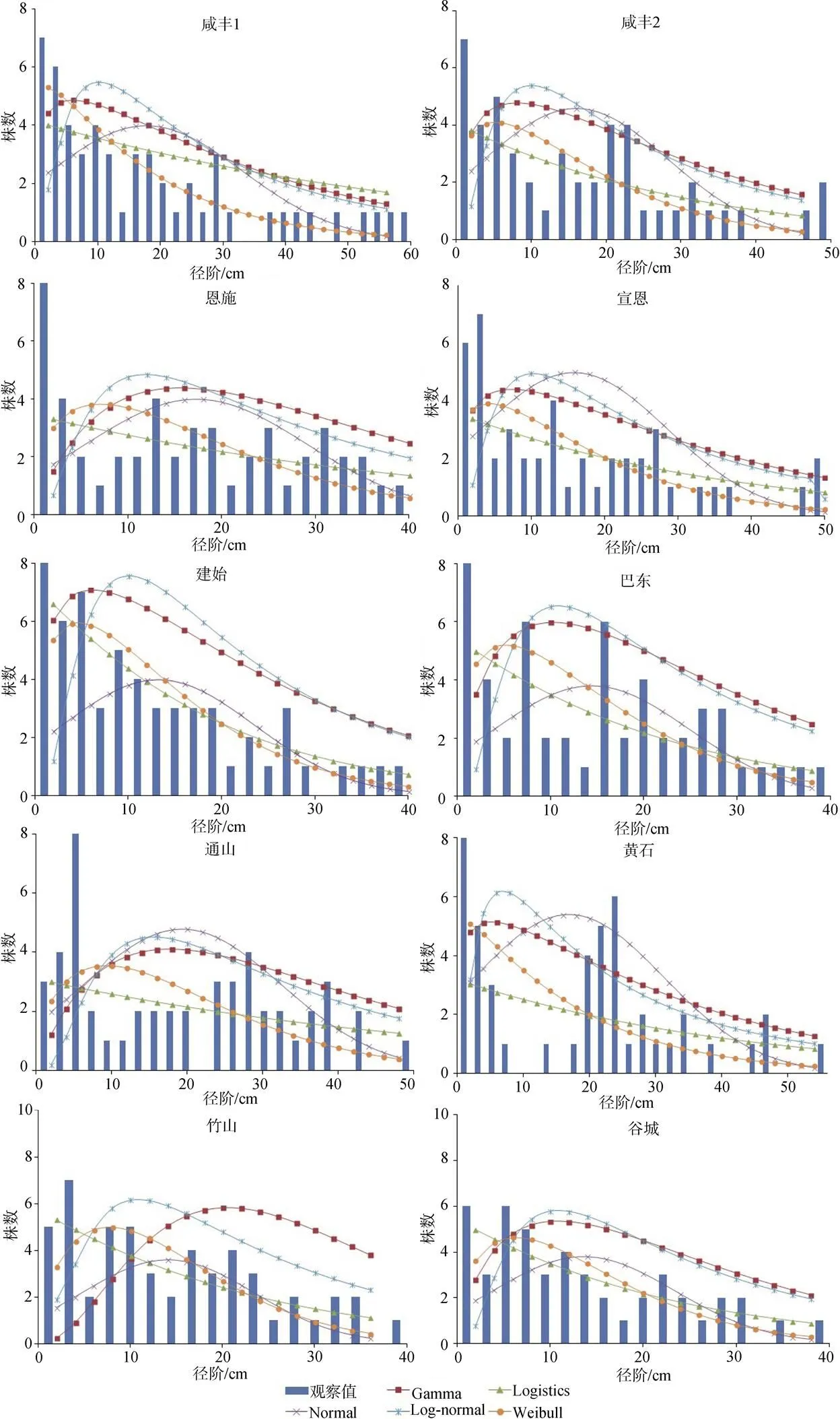
图1 林木直径分布的观测与模型拟合曲线

Figure 1 Observed and fitting curves of diameter distribution functions

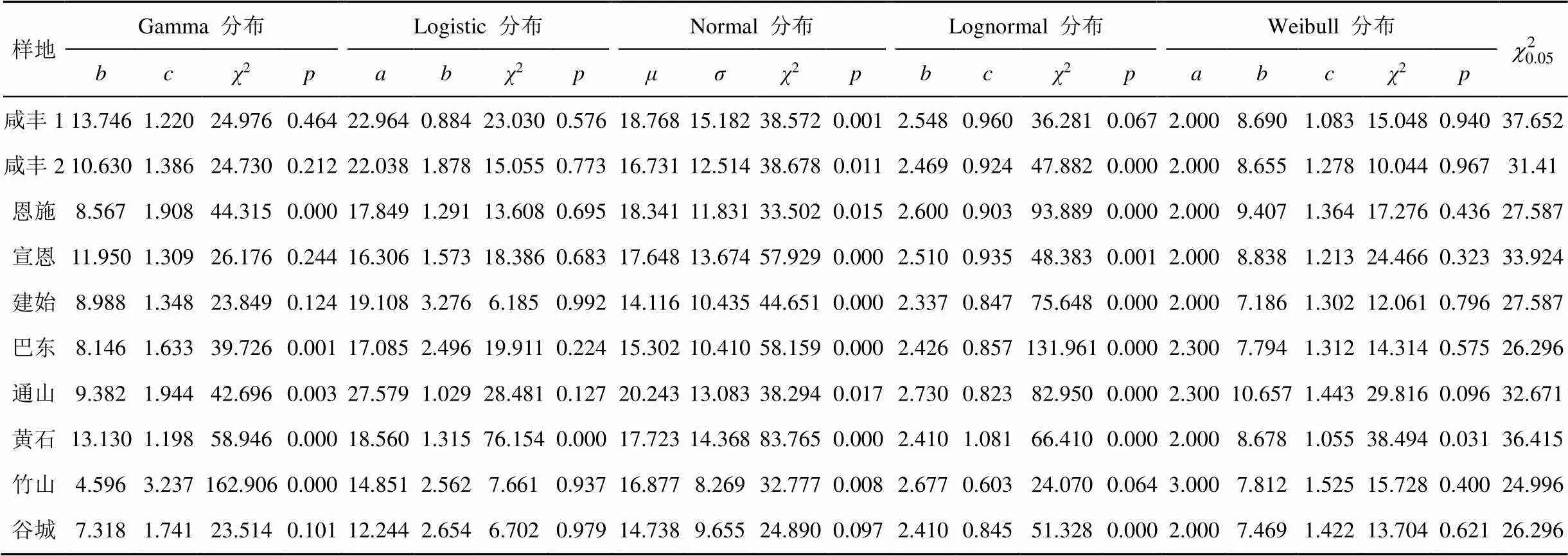
表5 红椿样地林木直径分布参数估计值

注: 各分布函数经2检验, 接受百分率见表6; 10个红椿样地中, 符合logistic分布和Weibull 分布函数的各9个, 其接受率最高, 均为90.0%。Gamma分布、normal分布和lognormal分布拟合的接受率分别为50.0%、10.0%和80%。对logistic和Weibull分布的2值进行配对样本T检验, 配对样本的=0.589>0.001, 不存在显著差异; 表明logistic和Weibull分布函数均适宜拟合红椿直径分布。

表6 红椿样地林木直径分布函数检验统计结果

表7 Weibull分布参数b、c回归分析

3.4 直径分布预测

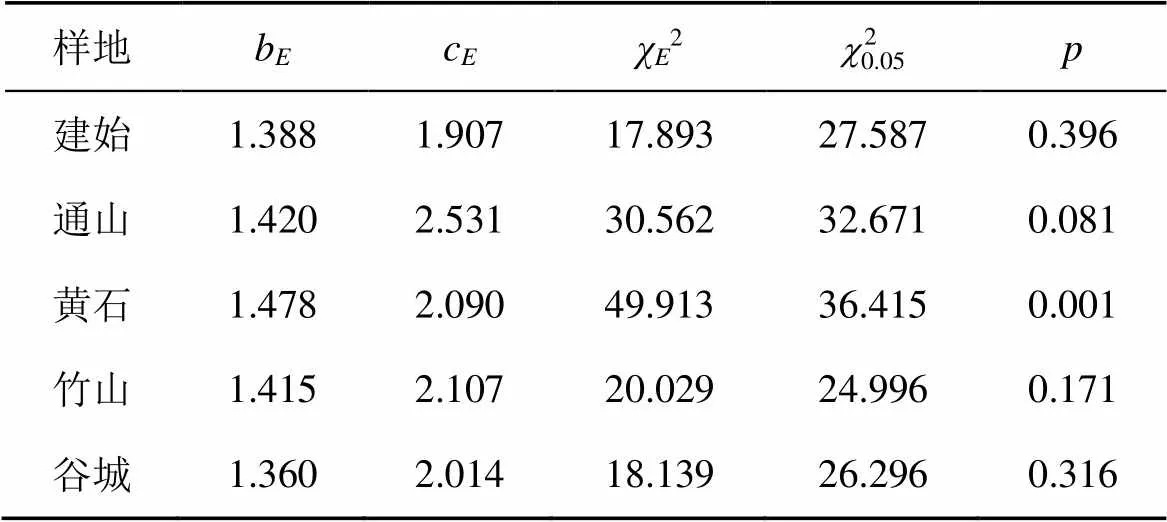
表8 Weibull分布预测效果

4 讨论与结论

红椿天然次生林林木的直径分布主要为左偏山状, 即反“J”型, 表明林木分布偏向中小径级。研究结论与巢林等[8]对中亚热带杉阔混交林直径分布研究, 李效雄等[26]对祁连山云杉林径级结构呈反“J”型结果相似; 与Meyer[27-28]等学者对大尺度范围下美国东北部林分直径分布, 以及他们对山毛榉、桦树、枫树、铁杉混交林林分直径分布研究时发现直径分布普遍呈反“J”型也很相似。

在大区域或高海拔梯度的研究中, 随小气候的变化, 地形一般通过改变光照、温度、水分等生态条件对树木生长产生作用[29]。红椿为强阳性树种, 尽管不同样地海拔、坡度和坡向不同, 但必须充分满足林冠层光照条件, 群落才能维持稳定。因此, 红椿常栖生于光环境较好的溪流、河道边或狭窄的林缘地带, 并出现小种群现象[30], 但群落外部光环境条件较好, 不同小环境下光照条件基本一直, 均能满足光照需求。随着径级增高, 对应直径的红椿林木株数相应减少, 在较高径阶时株数逐渐趋于平稳, 说明直径分布可反映林分曾经受到的干扰[5]。林内未能达到林冠层的红椿植株很难通过光环境筛, 导致直径8—16 cm的红椿幼树或中树植株死亡较多, 幼树数量相对增加, 直径分布的离散程度较小, 中等和略偏小直径的林木占大多数, 林分的峰度和偏度均会下降。

综合拟合优度排序为: Weibull分布≥Logistic分布>Gamma分布>Lognormal分布>Normal分布。模型比较表明, Weibull分布函数和Logistic分布函数均可较好地解释湖北地区红椿近成熟天然次生林林木直径分布规律, 从理论与实际观测结果都表现出了良好的适应性和灵活性。2检验表明, Logistic分布函数也能很好地解释10个样地红椿天然林林木直径分布, 但拟合优度略低于Weibull分布。Logistic分布函数较为适合偏度较小的林木直径分布拟合[31], 但模拟林分样地面积的大小、径阶宽度的划分等因素都会对林分直径分布模拟结果产生影响[8]。Logistic分布是否能够应用于较大范围红椿天然林直径分布模拟还有待进一步研究。

由于湖北红椿天然林林木直径分布影响因素复杂多变, 尤其是环境、人为干扰和树龄等因素存在较大差异, 在模型选择时, 应根据拟研究红椿林分的具体情况和研究定位综合考虑。林分因子和Weibull参数和经过回归后, 获得的直径分布参数估计值b和c, 代入Weibull函数预测红椿天然林林木直径分布, 效果较为理想。生长环境变化可能导致植物生长发生明显变化[32], 林木直径分布模型具有较高的时效性、敏感性和可操作性[33]。对于具体物种而言, 红椿是光敏感型濒危植物, 可以通过监测观测值与直径分布模型拟合值的差异变化, 合理调节林木直径结构, 如制造林窗等正相干预,以此促进林分中小径级红椿林木获得足够光资源, 突破生态幅狭窄带, 即突破造成红椿濒危的关键生理期, 提高模型拟合度。促进中小径级林木进入主林层和林下更新, 保护红椿资源并使其发挥群落生态功能。

[1] GADOW K V, ZHANG C Y, WEHENKEL C, et al. Chapter 2: forest structure and diversity[M]//PUKKALA T, GADOW K V. Continuous cover forestry. Springer, Berlin: Managing Forest Ecosystems, 2012.

[2] 雷相东, 唐守正. 林分结构多样性指标研究综述[J]. 林业科学, 2002, 38(3): 140—146.

[3] 陈昌雄, 黄宝, 林立法. 南平市延平区天然阔叶林直径分布的研究[J]. 福建林业科技, 2004, 31(1): 1–9.

[4] 惠刚盈, 胡艳波, 徐海. 结构化森林经营[M]. 北京: 中国林业出版社, 2007.

[5] OBIANG N L E, NGOMANDA A, HYAMA O, et al.Diagnosing the demographic balance of two light-demanding tree species populations in central Africa from their diameter distribution[J]. Forest Ecology and Management, 2014, 313: 55–62.

[6] 张连金, 胡艳波, 赵中华, 等. 北京九龙山侧柏人工林空间结构多样性[J]. 生态学杂志, 2015, 34(1): 60–69.

[7] DIAMANTOPOULOU M J, ÖZÇELIK R, CRECENTE-CAMPO F, et al. Estimation of Weibull function parameters for modelling tree diameter distribution using least squares and artificial neural networks methods [J]. Biosystems Engineering, 2015, 133: 33–45.

[8] 巢林, 洪滔, 林卓, 等. 中亚热带杉阔混交林直径分布研究[J]. 中南林业科技大学学报, 2014, 34 (9): 31–37.

[9] 汪求来. 广东省针阔混交林直径分布规律研究[J]. 林业调查规划, 2014, 39(6): 28–34.

[10] 褚欣, 潘萍, 李琦, 等. 闽楠天然次生林直径分布模拟研究[J]. 江西农业大学学报, 2019, 41(2): 273–280.

[11] 张雄清, 雷渊才. 北京山区天然栎林直径分布的研究[J]. 西北林学院学报, 2009, 24(6): 1–5.

[12] 雷娜庆, 铁牛, 刘洋, 等. 兴安落叶松天然林林分直径分布和树高分布[J]. 东北林业大学学报, 2017, 45(1): 90–93.

[13] 国红, 雷渊才. 蒙古栎林分直径Weibull分布参数估计和预测方法比较[J]. 林业科学, 2016, 52(10): 64–71.

[14] 张文辉. 裂叶沙参种群生态学研究[M]. 哈尔滨: 东北林业大学出版社, 1998.

[15] 汪洋, 陈文学, 明安觉, 等. 湖北红椿天然种群小叶表型性状变异研究[J]. 植物资源与环境学报, 2019, 28(2): 96–105.

[16] 李培, 阙青敏, 欧阳昆唏, 等. 不同种源红椿SRAP标记的遗传多样性分析[J]. 林业科学, 2016, 52(1): 62–70.

[17] 汪洋, 田玉娥, 甘小燕, 等. 湖北红椿天然居群表型变异地理趋势面研究[J]. 森林与环境学报, 2018, 38(3): 309–317.

[18] BLISS C L, REINKER K A. A log-normal approach to diameter distributions in even-aged stands [J]. Forest Science, 1964, 10:350–360.

[19] 陈瑞杰, 盖新敏, 翁怀锋, 等. 突脉青冈天然林主要种群直径分布结构特征的研究[J]. 福建林业科技, 2005, 32( 2): 27–30.

[20] NELSON T C. Diameter distribution and growth of loblolly pine [J]. Forest Science, 1964, 10(1): 105–114.

[21] DUAN Aiguo, FU Lihua, ZHANG Jianguo. Self-thinning rules at Chinese fir () plantations, based on a permanent density trial in southern China[J]. Journal of Resources and Ecology, 2019, 10(3): 315–323.

[22] 张岗岗, 王得祥, 刘文桢, 等. 火地塘林区不同径级华北落叶松结构参数研究[J]. 西北林学院学报, 2014, 29(6): 180–185.

[23] BORDERS B E, SOUTER R A, BAILEY R L, et al. Percentile-based distributions characterize forest stand tables [J]. Forest Science, 1987(33): 570–576.

[24] HAARA A, MALTOMO M, TOKOLA T. The-nearest-neighbor method for estimating basal-area diameter distribution[J]. Scandinavian Journal of Forest Research, 1997(12): 200–208.

[25] BURKHARTE H E, TOMÉ M. Modeling forest trees and stands[M]. Springer Netherlands, 2012.

[26] 李效雄, 刘贤德, 赵维俊. 祁连山青海云杉林动态监测样地群落特征[J]. 中国沙漠, 2013, 33(1): 95–100.

[27] MEYER H A. Structure, growth, and drain in balanced uneven-aged forests[J]. Journal of Forestry, 1952, 50(2): 85–92.

[28] MEYER H A, STEVENSON D D. The structure and growth of virgin beech-birch-maple-hemlock forests in northern Pennsylvania [J]. Journal of Agricultural Research, 1943, 67: 465–484.

[29] 池源, 郭振, 石洪华, 等. 北长山岛人工林健康状况评价[J]. 生态科学, 2017, 36(1): 215–223.

[30] WANG Yang, YUE Dan, LI Xinzhi. Genetic diversity ofpopulations based on SSR markers[J]. Journal of Resources and Ecology, 2020,11(5): 466–474.

[31] 王明亮, 孙德宙. Logistic分布预测林分直径结构的研究[J]. 林业科学研究,1998,11(5): 537–541.

[32] 彭玉华, 谭长强, 郑威, 等. 环境因子对广西红锥幼林生长的影响[J]. 生态科学, 2020, 39(2): 90–94.

[33] 惠刚盈, 盛炜彤. 林分直径结构模型的研究[J]. 林业科学研究, 1995, 8(2): 127–131.

Diameter distribution of natural near-mature secondaryforests in Hubei region

ZHONG Changlong1, SHI Weihua2, LI Guoxiu1, WANG Yang1, SONG Fei3, *

1. Hubei Ecology Polytechnic College, Wuhan 430200, China 2. Management Office, Duheyuan Nature Reserve, Zhushan 442200, Hubei, China 3. Hubei Academy of Forestry, Wuhan, Hubei 430075, China

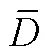
; natural near-mature secondary forest; diameter distribution; fitting; Weibull function

10.14108/j.cnki.1008-8873.2022.06.014

S792.33

A

1008-8873(2022)06-114-09

2020-10-08;

2020-12-11

湖北省科学技术厅公益性研究项目(402012DBA40001);中德财政合作林业重大研究项目(zdczhz2021ky09); 中德财政合作中国南方(湖北省)森林可持续经营项目(BMZID200665778); 湖北省教育厅科研项目(B20160555)

钟昌龙(1980—), 男, 湖北武汉人, 副教授, 主要从事景观规划与生态恢复研究, E-mail: 67322082@qq.com

通信作者:宋菲, 女, 工程师, 主要从事植物栽培与育种研究, E-mail: 506448615@qq.com

钟昌龙, 施维华, 李国秀, 等. 红椿近成熟天然次生林直径分布[J]. 生态科学, 2022, 41(6): 114–122.

ZHONG Changlong, SHI Weihua, LI Guoxiu, et al. Diameter distribution of natural near-mature secondaryforests in Hubei region[J]. Ecological Science, 2022, 41(6): 114–122.