面结构光测量曲面特征的不确定度评估
2022-09-17程银宝赵一帆罗哉王中宇王学影
程银宝,赵一帆,罗哉*,王中宇,王学影
(1.中国计量大学 计量测试工程学院,浙江 杭州 310018;2.北京航空航天大学 仪器科学与光电工程学院,北京 100191)
1 引言
近年来,自由曲面的高精度测量在汽车、飞机、模具等制造业呈现爆炸式增长[1-2]。自由曲面面形是无法用函数表达式表示的非对称复杂曲面,基于有限点的传统测量无法提供足够的测量信息。三维测量技术具有非接触扫描、测量速度快、实用性强等优点,在逆向工程、质量检测[3]等领域发挥着重要作用。其中,结构光式扫描仪因其精度高可以用于复杂曲面测量[4]。测量不确定度,及不确定度分析和溯源是计量型仪器测量的基本要求。基于面结构测量曲面的技术虽然逐渐成熟,但其测量结果的不确定度评估仍是难点,这也限制了结构光式三维测量技术在计量领域的应用。因此,对面向具体任务的面结构光测量信息进行可靠的不确定度评价是亟待解决的问题。
不确定分析对于被测物的质量评价以及量值溯源均必不可少。Fortmeier等[5]展示了全场测量倾斜波干涉仪对于非旋转对称工件的形状测量,可以校准其半径和球度,可用于非球面和自由曲面的可追溯参考。Ren等[6]基于最小二乘原则建立误差评定的数学模型,分析了曲面测量中采样策略和评估方法引起的不确定性,基于蒙特卡洛模型分析了测量评定中的相关不确定度。Kim等[7]利用蓝光扫描仪对基台角度的重复性和复现性进行了评定。Susana等[8]将蓝光扫描仪和三坐标测量机(Coordinate Measuring Machine,CMM)的轮廓度测量值进行比较,分析不同视场下的测试效果,给出了每种配置下的精度。He等[9]采用单纯性法和差分进化结合的算法优化轮廓度误差模型,该方法优于最小二乘法。温秀兰等[10]针对自由曲面的特点,使用CMM设定多种曲面测量策略,通过比较轮廓度误差寻求最优采样策略,考虑了测量策略的影响并进行优化,但是没有分析测量策略不同引入的不确定度差异。陈满意等[11]基于Bootstrap法对测量点数均匀分布的曲面实现了最佳适配不确定度评定,但此方法计算量大,需多次测量。王东霞等[12]通过拟粒子群优化算法实现曲面定位,在已知CAD模型下得到了曲面轮廓度误差,以均方根误差和峰谷误差指标综合评定了自由曲面。程银宝等[13]结合经典的精度理论,分析了CMM繁杂的不确定度来源,建立普适性的黑箱评定模型,通过实例验证了此方法符合国际标准测量不确定度表示指南(Guide to the Expression of Uncertainty in Measurement,GUM)中的基本原理[14]。
综上所述,学者们更关注轮廓度误差的评定算法,给出的不确定评定是不完善的,不仅没有分析仪器自身的误差源,而且对于评定算法的数据处理引入的不确定度分量是忽略不计的,但是在不确定度评定中应不能遗漏或者重复计算各不确定度来源。因此,本文针对蓝光扫描仪测量轮廓度的不确定度来源进行详细分析,并给出量化方法。测量系统的输入量和输出量存在因果关系,可以由因得果,也可以由果析因。由于缺少可溯源测量制造曲面的评定方法,自由曲面在精密加工行业的应用仍有阻碍。本文采用海克斯康Primescan系列蓝光扫描仪采集点云数据,依据Polyworks软件[15]处理并计算被测工件的曲面轮廓度,采用2种不同的方法分析测量系统的不确定度来源并进行不确定度建模。根据测量原理以及评定准则,从误差溯源方面建立透明箱模型;从量值统计分析测量结果的量值特性指标建立黑箱模型,分别采用两个模型实现此任务的不确定度分析。
2 测量原理
2.1 蓝光扫描仪的测量原理
蓝光扫描仪是基于双目视觉构成的光栅投影系统[16]。中间的光栅传感器发射多条投影结构光栅至工件表面,光栅经物体表面的高度调制发生变形,变形后的光栅包含工件的表面信息,经相机编码匹配两张照片采集的信息,实现对应的解码计算,经三角测量法得到物体的三维数据。其测量原理如图1所示。
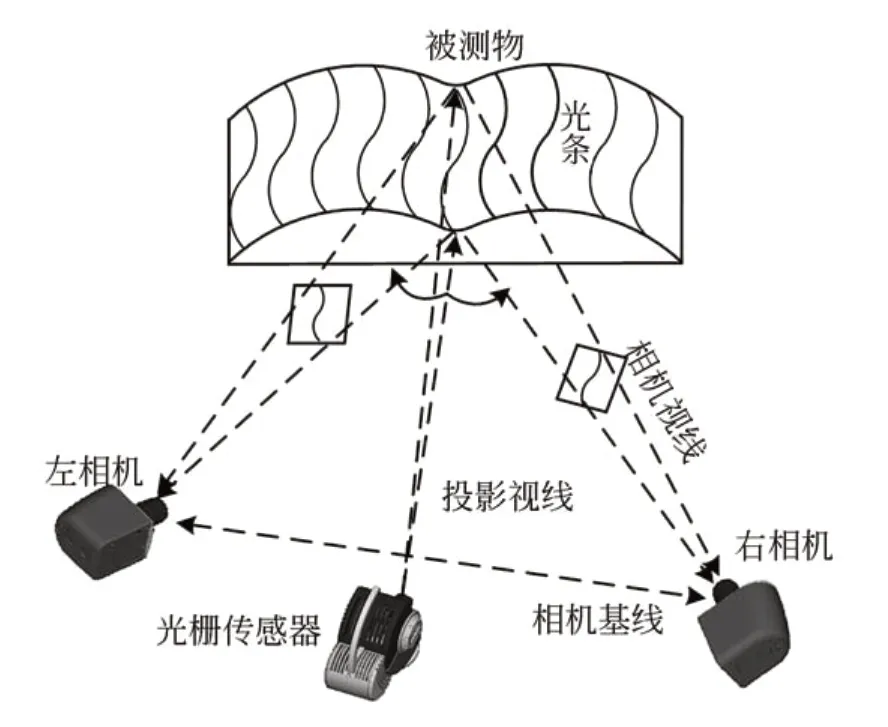
图1 蓝光扫描仪的测量原理Fig.1 Measurement principle of blue light scanner
2.2 自由曲面形状特征的评定准则
当测量曲面不存在加工与检测误差时,两组曲面会完美的重合。但是由于加工、检测误差的存在,测量曲面相对于理想曲面会存在一定的偏差和扰动。依据国家标准[17],曲面轮廓度误差值是被测实际轮廓相对于理想轮廓的变动情况,是通过坐标转换统一坐标系得到的。在已知CAD数模的实际测量过程中,假设点云数据所在的测量坐标系为o1-t1t2t3,CAD数模所在的设计坐标系o2-e1e2e3,点 云 数 据 中 的 极 大 值 点 为Q(xM,yM,zM),经T(R,D)坐标旋转平移变换后,统一在设计坐标系下,可得其极大值点相应的定位点为S(xL,yL,zL),与定位点相对应的最近点是P(x#,y#,z#)。其轮廓度误差是定位点和最近点的偏差的2倍,坐标转换过程如图2所示。

图2 曲面轮廓度的评定准则Fig.2 Evaluation criteria of surface profile
3 基于透明箱模型的不确定度分析与建模
3.1 不确定度分析
基于误差源分析的透明箱模型是指在充分了解测量原理后,被测参数与每个输入量之间都可以通过函数表达式得到,且每一个输入量带来的影响都可以经计算表达出来,可以通过函数关系量化出被测参数与误差源的传递系数[18]。
对于CAD模型已知的自由曲面,计算轮廓度误差需要进行定位,将测量点从测量坐标系转换到设计坐标系下[19]。假设实测点集中的极大值点为Q(xM,yM,zM),与CAD数模配准后的定位测量点设为S(xL,yL,zL),CAD数模上与极值点相对应的最近点设为P(x#,y#,z#)。将实测点集统一在理论点集坐标系下,其坐标变换可以表述为:

其中:D表示在X,Y,Z轴方向的平移参数;Rx,Ry,Rz表示在X,Y,Z轴方向的旋转参数。
假设θx,θy,θz分 别表示实测点集 绕 坐 标 轴旋转的角度,Δx,Δy,Δz分别表示实测点集绕坐标轴平移的分量。根据坐标转换,式(1)可转换为:

其中:sx表示sinθx,同理可得sy,sγ的含义;cx表示的是cosθx,同理可得cy,cγ的含义。
通 过 式(2)可 以 得 到Q(xM,yM,zM)到S(xL,yL,zL)的转换公式为:

根据定义,曲面轮廓度的函数表达式为:
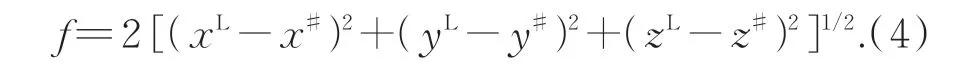
将式(3)代入式(4)中,其函数表达式可转换为:

3.2 不确定度建模
分析式(5)可知,轮廓度误差与测量极大值点坐标、转换参数和最近点坐标有关,而最近点是经坐标变换后确定的,不用考虑最近点引入的不确定度。多次测量会使得测量极大值点之间存在不确定度,也会导致变换参数矩阵之间存在不确定度,而且具有相关性。假定极大值点在3个方向的不确定度分量是互相独立的,而转换参数之间是具有相关性的。根据方差合成定理以及不确定度传播规律,可得自由曲面轮廓度的不确定度表达式为:

将6个转换参数看作是统计量,得到n组旋转平移量,其协方差矩阵表达式如下:

在同一条件下重复测量n次,测量极大值点可由n次测量结果计算方差表示其坐标的不确定度。各个变量的灵敏度系数通过对式(5)求偏导得到。
4 基于黑箱模型的不确定度分析与建模
4.1 不确定度分析
基于量值统计的黑箱模型是指将复杂的函数关系简化成具有激励源输入的测量方法,其优点是假定各个不确定度分量的灵敏度系数为1,省去了偏导求解的复杂计算过程,只需要找出不确定度分量即可。蓝光扫描仪在获取和处理三维点云信息的过程中涉及许多误差影响,这些误差使得采集的点云数据精度受限,复杂的测量任务必然伴随着量值传递,而测量系统的误差则伴随着量值传递体现在测量结果中。本文通过分析整个测量系统的测量原理和评定准则,从黑箱模型的角度将仪器示值误差、自校准误差、点云拼接误差、点云配准误差、重复性、复现性以及仪器分辨力等量值特性指标作为测量系统的不确定度分量,为评价测量系统提供支持。
4.2 不确定度建模
蓝光扫描仪的说明书没有给出示值误差,故需要设计实验得到仪器的示值误差。结合实验条件采用陶瓷标准球作为实验装置,根据国家计量技术规范JJF1059.1-2012《测量不确定度评定与表示》,测量结果的平均值和重复性实验以10次的测量结果为佳[20],取其重复性均值降低随机误差的影响,假设其服从均匀分布,示值误差量化后为:
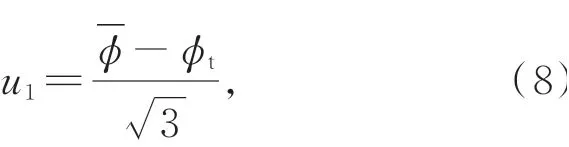
蓝光扫描仪在使用前需要对相机进行自校准,将相机的镜头畸变、硬件结构误差合成,经Optocat软件处理后可得误差为Ubd,则自校准误差引入的不确定度分量为:

三维数据的拼接是将两个或者两个以上的点云集合转换到同一坐标系下[21]。由于蓝光扫描仪的测量视角较小、被测工件超出其测量范围,扫描一次不能实现工件上轮廓度的测量,需要多角度多次扫描。在测量时,调整扫描仪的角度以及快门设置,使得点云集合之间有重合部分,经拼接实现工件表面信息的重构,数据点集之间进行拼接时存在姿态偏差,多次扫描必然会引起误差传递。
数据拼接的实质是通过旋转、平移参数实现坐标转换。实验选择包括曲面的两个区域,分别扫描10次,将10次拼接重合部分的标准偏差si的均值作为点云拼接引入的不确定度分量,即有:

在CAD数模已知的前提下,实测点集经拼接后需要和CAD进行配准。大多数软件都利用同名点的坐标解算,通过旋转和平移把测量点统一在CAD数模所在的坐标系实现坐标配准,因此在对齐过程中配准误差是不可避免的。将10次坐标配准的标偏差ri的均值作为配准引入的不确定度分量,即:

重复性是不确定度评定必不可少的分量之一,经上述拼接、配准后计算轮廓度误差值。重复性引入的不确定度分量用贝塞尔公式表示为:

其中:fi表示轮廓度误差;n表示测量次数;N是指取N次测量结果的平均值作为最佳估计值。
不同测量人员独立重复测量m组,求出每一组测量列的平均值,将每组得到的均值重新组成一个测量列,将新的测量列作为复现性引入的不确定度分量,即:
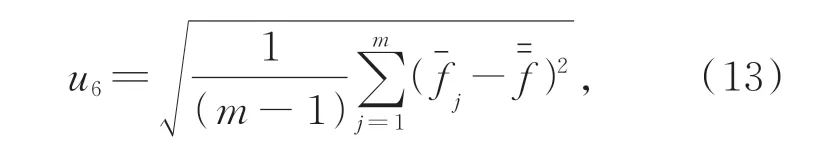
式中:m为测量的组数;为第j组重复测量列的均值为m组测量列的均值的均值。
即使蓝光扫描仪提前预热,依然无法完全消除稳定性的影响,在所有测量条件都不改变的情况下,对工件间隔24 h重复测量3次,每次测量10组数据,计算每组的轮廓度均值,得到最大值fmax和最小值fmin。假设服从高斯分布(分布因子为0.5),则稳定性引起的不确定度分量为:

将上述不确定度分量进行合成,可得基于黑箱模型的不确定度分量为:
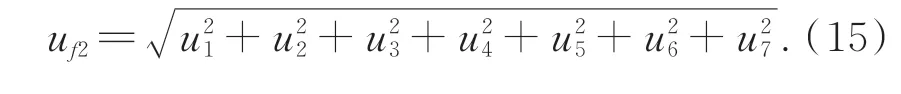
5 测量实验与结果
使用海克斯康的PrimeScan扫描仪,其视场为130 mm×85 mm×78 mm,分辨率为69 μm,工作距离为370 mm。实验选择仪器厂家海克斯康提供的标准实验件,此工件上的曲面为自由曲面。故以某工件上的曲面轮廓度为被测对象。在恒温恒湿的实验室内,通过Optocat软件完成蓝光扫描仪对工件表面信息的采集。Optocat软件是和蓝光扫描仪配套的三维采集软件,涉及扫描过程的整个任务范围。其数据采集过程如图3所示。

图3 蓝光扫描仪测量曲面轮廓度Fig.3 Measurement of surface profile by blue scanner
在Polyworks软件实现曲面轮廓度误差的测量。综上可知,曲面轮廓度误差与坐标转换有关。曲面轮廓度评定时的操作步骤如图4所示。
5.1 透明箱模型的不确定度评定
在Polyworks中,采用“最佳拟合数据至参考对象”,以综合偏差最小为目标来求取最佳匹配时的R和T,当迭代结果小于10-6时满足最佳匹配,采样选择“1/1”,经多次实验调整,将最大角度设置为45°,最大距离设置为0.1 mm,使用“N点对齐”后实现预对齐。此时10次测量实验坐标配准的迭代值分别为0.111×10-6,0.106×10-6,0.109×10-6,0.288×10-6,0.182×10-6,0.262×10-6,0.200×10-6,0.115×10-6,0.225×10-6,0.189×10-6。通过“最佳拟合对齐”操作实现精确对齐,其坐标转换矩阵如下:

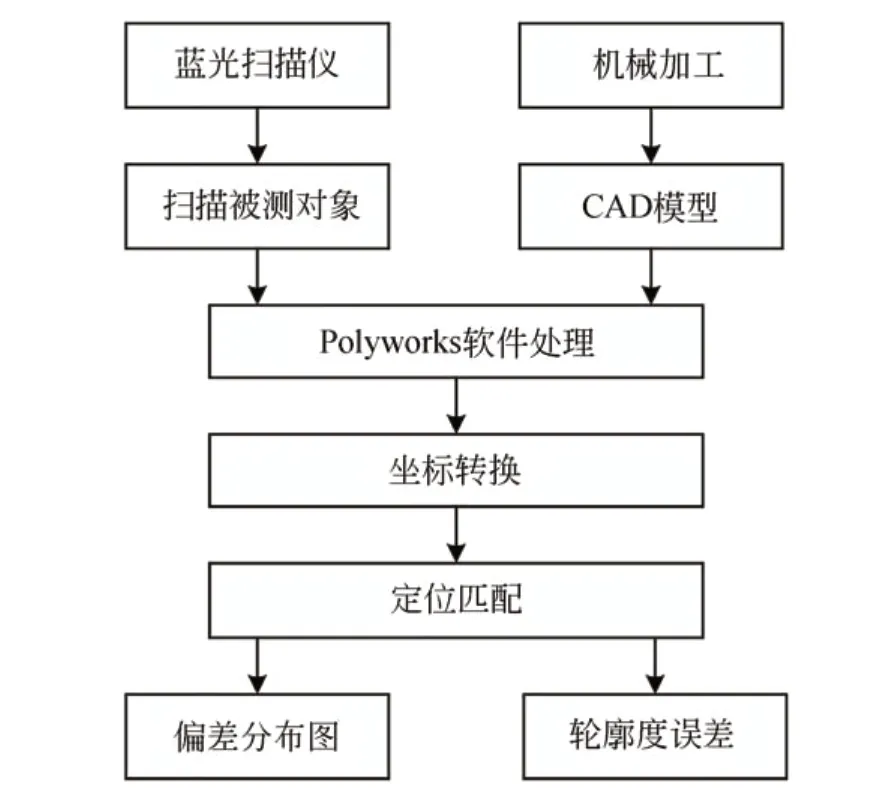
图4 曲面轮廓度评定流程Fig.4 Flow chart of surface profile evaluation
根据上述坐标转换矩阵可以求得旋转平移量。在蓝光扫描仪的扫描角度和快门设置不变的情况下,短时间内重复扫描10次,得到的旋转平移参数如表1所示。

表1 旋转平移参数Tab.1 Values of rotation and translation parameters
SPSS软件不仅提供数据处理和数据分析等操作,而且涵盖各种方法和模型,对于协方差矩阵的求解是便利的。将表1中数据利用SPSS软件计算可得到其协方差矩阵值为:
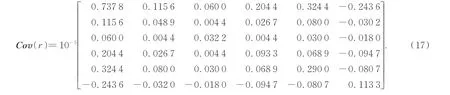
测量10次,每次测量都有一个定位点和相应的最近点,测量数据如表2所示。通过坐标转换可以得到定位点在测量坐标系下的极大值点。极大值点在3个方向的不确定度可依据贝塞尔公式计算。将上述数据带入到式(5)中并求偏导,可得灵敏度系数如表3所示。
将上述所得结果带入式(6)中,最终可得曲面轮廓度的不确定度uf1=0.020 mm。
取包含因子为k=2,扩展不确定度为:


表2 定位极值点及最近点的坐标值Tab.2 Locating coordinate values of extreme points and nearest points (mm)

表3 灵敏度系数Tab.3 Sensitivity coefficients (mm)
5.2 黑箱模型的不确定度评定
实验采用标准球作为校准装置,采用海克斯康的global S 09.12.08-green三坐标测量机标准球。坐标测量机的最大示值允许误差为:MPEE=(1.7+2.8 L/1 000)μm。其标准球直径值30.005 5 mm是三坐标测量机的实测值,则标定实验引入的测量不确定度为:

对于用标准球标定蓝光扫描仪示值误差来说,标准球直径值30.005 5 mm的不确定度为1 μm,可以忽略不计。
蓝光扫描仪对标定后的标准球重复测量10次,经拟合后得到标准球的实测值,取其均值与理论值进行比较,消除随机误差的影响,从而得到蓝光扫描仪的示值误差。其实验过程及拟合效果如图5所示。
经最佳拟合后,标准球直径的10次测量结果为30.022,30.018,30.020,30.024,30.024,30.021,30.020,30.018,30.011,30.024 mm。将上述数据代入式(8)中得到:
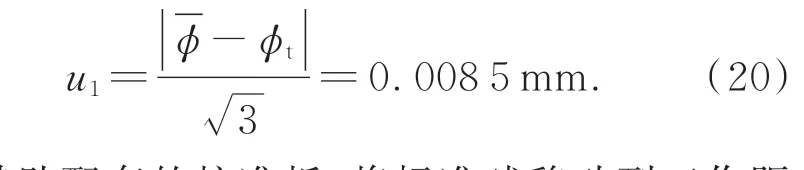

图5 蓝光扫描仪测量标准球Fig.5 Measuring standard ball by blue light scanner
借助配套的校准板,将标准球移动到工作距离内,使用9个标准位置执行校准,不仅对照相机的图像计算校准,而且对投影设备也进行校准。校准完成后,可得标定误差为Ubd=6 μm,则标定误差带来的不确定度分量为:

在数据拼接前需进行预处理,通过非接触测量获取的数据,在曲率变化较大的表面或者尖锐边缘会出现噪声点,故先去除多余的杂点和噪声,再调用Polyworks软件的“最佳拟合数据至数据对象”操作实现拼接,重合部分的拼接结果如图6所示。重合部分经拟合后得到的拼接偏差如图7所示。

图6 数据点集的拼接Fig.6 Splicing of data point sets

图7 数据点集重合部分的偏差Fig.7 Deviation of overlapping part of data point set
10次拼接的标准偏差分别是0.013,0.013,0.014,0.013,0.013,0.012,0.013,0.014,0.014,0.013 mm,带入到式(10)可得点云拼接引入的平均标准偏差,即标准不确定度分量为:

将CAD数模和实测点集分别作为参考对象和数据对象,经多次实验,设置最大距离为1 mm以及最大角度为45°,实现实测曲面与理论曲面的最佳匹配对齐,点云至数模的配准示意图如图8所示。

图8 点云至CAD数模的坐标配准Fig.8 Coordinate registration from point cloud to CAD
由于评价对象是曲面轮廓度,故在Polyowrks软件只选择制定的曲面区域,该区域所有的采集点都参与计算,曲面部分的点云至CAD数模配准结果的偏差分析图如图9所示。10次配准结果的标准偏差分别是0.017,0.017,0.016,0.016.0.016,0.016,0.017,0.016,0.016,0.016 mm,带入到式(11)可得点云配准引入的平均标准偏差,即标准不确定度分量为:

图9 点云至数模配准的偏差图Fig.9 Deviation graph of point cloud to digital-analog registration

不同测量人员测量的轮廓度如表4所示。

表4 不同测量人员的测量结果Tab.4 Measurement results by different measuring personnel (mm)
测量结果的重复性反映的是随机效应的影响,从表中抽取某位操作人员的测量数据作为重复性考察指标。将表4中操作人员A的测量数据代入式(12)中,可得重复性引入的不确定度分量为:

将操作人员A的数据带入式(13)中,可得复现性的不确定度分量为:

蓝光扫描仪和校准板提前24 h处于恒温恒湿的环境中,减少其特性因时间流逝而发生微小变化,正式测量前传感器提前打开30~60 min,使得照相机和镜头预热到合适的工作温度。在测量条件不变的情况下,3天测量中的最大均值fmax=0.120 6 mm,最小均值fmin=0.113 1 mm。将它们代入式(14)可得稳定性引入的不确定度分量为:

根据方差合成定理,整个测量任务的合成标准不确定度为:

取包含因子为k=2,扩展不确定度为:

5.3 评定结果比较
误差源分析的不确定度主要与测量的极大值点和相应的最近点坐标以及转换参数有关。量值统计分析主要是从测量结果的量值特性作为不确定度分量。后者较前者计算简单、效率高。如表5所示,其标准不确定度相差3 μm,扩展不确定度相差6 μm,满足精度要求。量值统计方法可以用于蓝光扫描仪面向曲面轮廓度的不确定度可靠评定。

表5 两种评定模型的比较Tab.5 Comparison of two evaluation models(mm)
6 结论
为解决面结构光类仪器测量自由曲面特征的不确定度溯源问题,本文基于误差源分析和量值统计方法提出了两种不同的不确定度分析思路,分别建立了透明箱模型和黑箱模型,相比于透明箱模型,运用黑箱模型实现轮廓度的不确定度评定具有简便、高效的优点。实验结果表明,透明箱模型得到的自由曲面测量结果的不确定度为0.020 mm,黑箱模型得到的自由曲面测量结果的不确定度为0.023 mm,两者之间的偏差在μm级,验证了简单高效的黑箱模型可以实现蓝光扫描仪面向曲面轮廓度的不确定度可靠评定。本文提出的方法为自由曲面轮廓度表征的质量指标提供了量化手段,解决了结构光式扫描仪及类似三维测量仪器的自由曲面测量不确定度溯源问题。
