增强分布估计算法求解双边装配线第二类平衡问题

张腾飞，胡 蓉,，钱 斌,，张梓琪，吕 阳

（1.昆明理工大学信息工程与自动化学院,云南昆明 650500；2.昆明理工大学机电工程学院,云南昆明 650500）

1 引言

双边装配线是新能源汽车、军工等制造业中广泛采用的生产方式.双边装配线平衡程度决定制造系统生产率［1］，该平衡程度由生产节拍（Cycle Time，CT）内各工作站的繁忙状态决定.研究求解双边装配线平衡问题的高效算法对于制造业提高生产效率具有实际意义［2］.

双边装配线第二类平衡问题（Two-side Assembly Line Balancing Problem of type-Ⅱ，TALBP-Ⅱ）研究给定工作站前提下如何最大化生产效率.针对TALBP-Ⅱ，唐等［3］设计一种新颖的离散人工蜂群（Discrete Artificial Bee Colony，DABC）算法进行求解.Li［4］等利用改进迭代贪婪（Iterative Greed，IG）算法对其求解.此外，变邻域搜索算法［5］、殖民竞争算法［6］、蚁群算法［7］等应用于TALBP-Ⅱ也取得不同程度的优化效果.上述研究主要以CT 为优化目标对TALBP-Ⅱ进行建模和求解.当CT 达到最优值时，并不能保证工作站的平滑指数（Smoothing Index，SI）同时最优.由于SI 影响双边装配线的负载均衡，进而影响生产效率.因此有必要将SI作为次级优化目标对TALBP-Ⅱ进行建模与求解.

分布估计算法是一种基于概率统计的新型智能算法［8］，目前已成功用于求解传统ALBP［9］、机器人作业的ALBP［10，11］、含生产与装配过程的集成调度问题［12～14］.分布估计算法利用针对问题结构特点设计的概率模型来学习和积累优质解中的结构信息，通过采样概率模型可生成问题的新优质解.这种“学习-采样”的方法能引导算法较快地搜索到解空间中的优质区域.

综上，本文针对TALBP-Ⅱ，建立以CT和SI 为主次优化目标的排序模型，提出增强分布估计算法进行求解.在算法初始化阶段，设计一种自适应策略生成初始节拍来提升初始解质量.在全局搜索阶段，设计符合问题结构特点的概率模型来学习生成解的信息，使算法能够快速搜索到优质解区域.在局部搜索阶段，设计适合主次目标的局部搜索策略，提升算法局部搜索能力.此外，提出利用空闲时间最大值对新解可行性进行快速判断的方法，节省较多评价解的时间，从而提升算法搜索效率.

2 问题模型

2.1 问题描述及相关符号

TALBP-Ⅱ描述如下：在拥有m组工作站的双边装配线上装配一件包含n项工序的产品.同一工作站可装配多项工序.L（R）型工序只能由工作站左侧（右侧）装配.E 型工序由任意侧装配.装配过程须满足装配顺序约束.在此条件下，寻找使生产效率最大的可行解.表1为本模型中所用符号及说明.

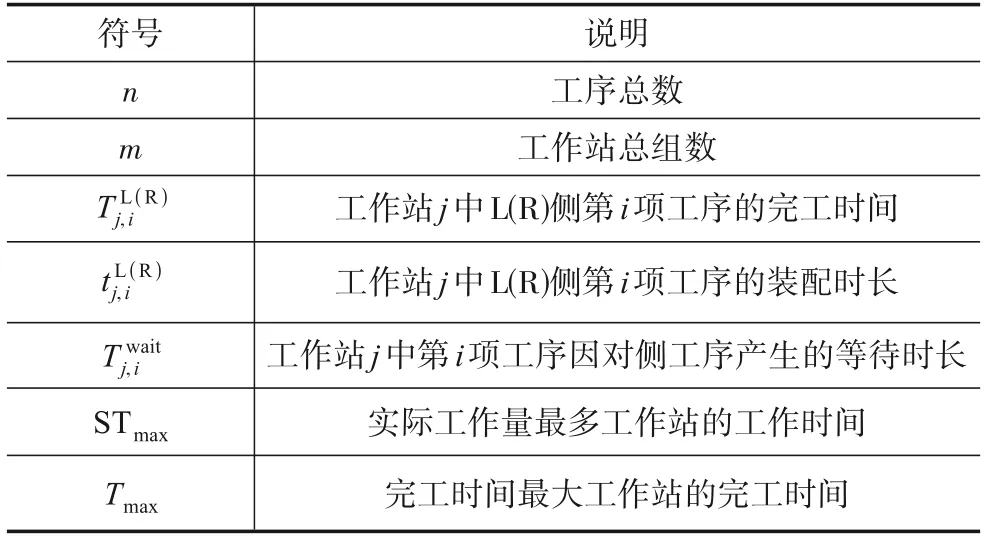
表1 符号及说明

2.2 TALBP-Ⅱ排序模型

设集合Π中包含所有满足TALBP-Ⅱ问题约束的可行解.优化目标为在Π中找到一个最优解，使该解满足最小CT且该CT下SI也最小，即：

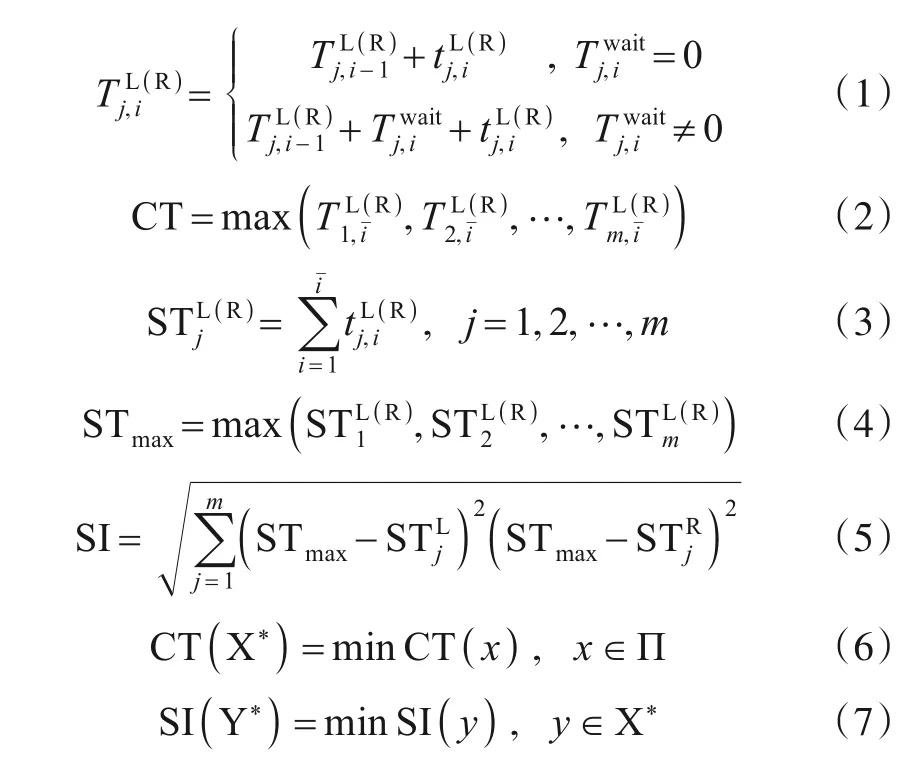
式（1）用于计算工作站中各工序的完工时间.式（2）用于计算生产节拍，iˉ表示工作站中最后一项工序.式（3）用于计算工作站的实际工作量.式（4）计算实际工作量最多工作站的工作时间.式（5）用于计算平滑指数.式（6）表示在解空间中找到满足CT最优的解集合.式（7）表示在CT 最优的解集合中找到满足SI 最优的解.

3 TALBP-Ⅱ中SI的分析与证明

在双边装配线中可推导如下性质：

性质1给定工作站数目和生产节拍，若x是可行解，且工序间空闲时间为零，则CT和SI可同时优化.

性质3给定工作站数目和生产节拍，x是可行解.在满足约束条件下，将工作站j中工作量较多侧工序i移入对侧.若满足，则SI得到优化.

性质3证明同性质2.性质1指出，针对完成时间最大的工作站，减小该站IDTmax和STmax是优化主要目标的两种途径.而性质2和性质3 指出，当主要目标达到最优或近似最优时，次要目标仍可能存在优化空间.因此，性质2 与性质3 为进一步优化TALBP-Ⅱ的次要目标提供了方法.综合利用性质1 至性质3，可实现主次目标的整体优化.

4 EEDA算法设计

EEDA 主要包括初始生产节拍设置方法、可行解快速判断方法、全局和局部搜索方法.EEDA 求解TALBP-Ⅱ的算法流程如图1 所示.生产节拍既作为优化目标，同时又与生成解时约束条件有关.本文生产节拍约束的更新方式如图1所示，当找到满足约束条件的可行解时，生产节拍约束将缩减.该更新方式能够保证生成新解时生产节拍约束始终小于历史最优生产节拍，进而使搜索过程始终沿着生产节拍最小化方向前进.

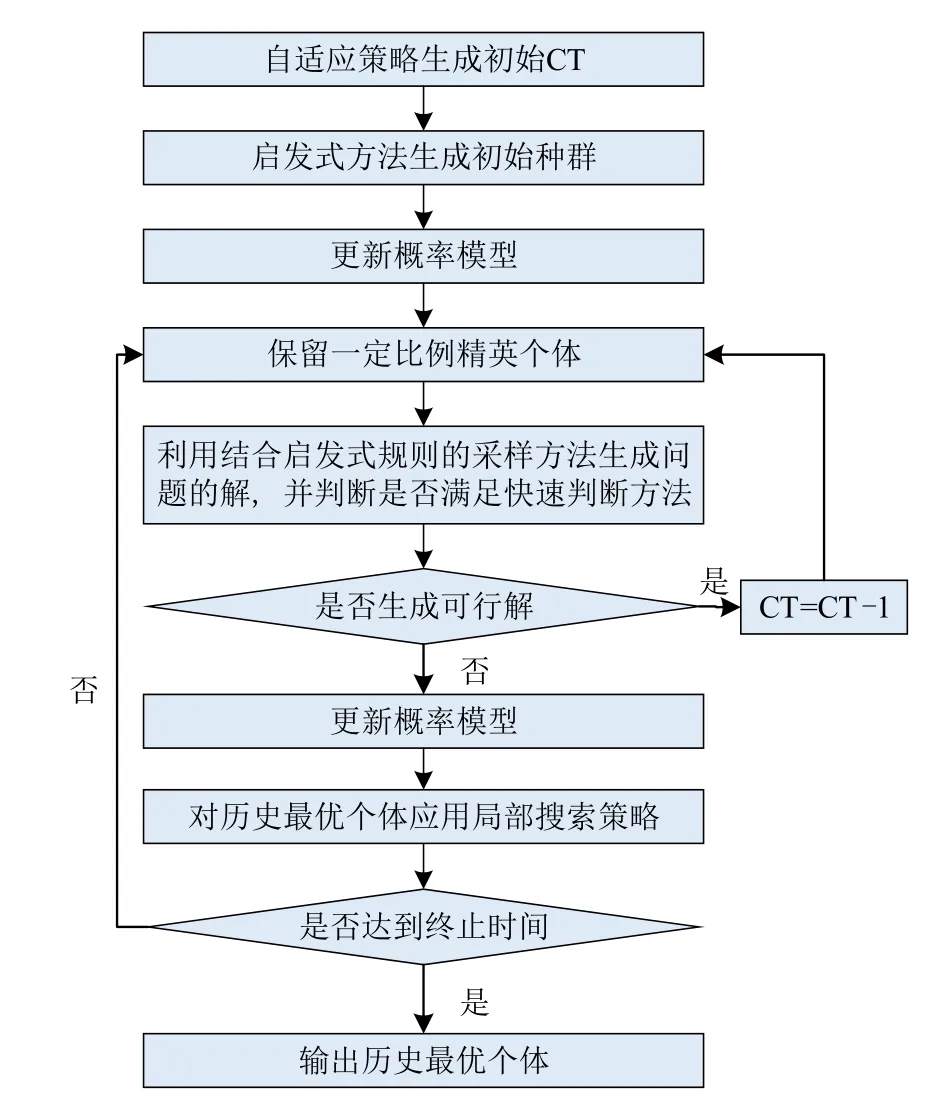
图1 EEDA算法流程图

4.1 生成初始CT的自适应策略

以a×LB(a∈(1，2))作为初始CT存在不足.例如，a取值偏大易使搜索过程变慢，a取值偏小则可能无法找可行解.为克服上述问题，本文提出一种自适应策略来生成初始CT，具体如算法1.其中，LB 表示CT 下界［3］.启发式规则确定分配方向具体为，优先选择空闲时间较大一侧工作站，仅当不存在满足该侧约束的工序时选择对侧工作站.确定分配工序具体为，在工序集中优先选择产生空闲时间最小的工序来分配，仅当存在多个优先级相同的工序时随机选择工序.

4.2 快速判断方法

快速判断方法是基于问题特性，利用最大允许空闲时间来判断生成解是否为可行解.最大允许空闲时间由式（8）计算.生成解过程中产生的空闲时间与最大允许空闲时间相比较，若前者大于后者，则生成解为不可行解.若生成完整解中前者小于等于后者，则生成解为可行解.通过提前判断生成解的可行性能够提高算法的执行效率.

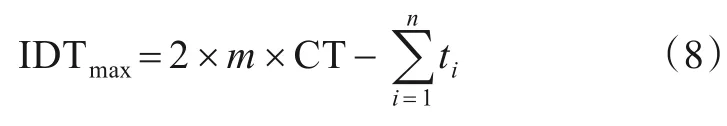
4.3 全局搜索策略

在EEDA中设计一种结合4.1节启发式规则的采样方法来生成问题的解，并基于该方法对问题解空间展开全局搜索.

4.3.1 概率模型

（1）建立概率模型

设π1，π2，…，πn为生成解时的工序分配排序.矩阵Pi，j，k表示三维概率模型.模型中记录了排序中三个工序被连续选择的概率.概率值越高，工序组合表现越好.

（2）结合启发式规则的采样方法

π1，π2由启发式方法选择，π3，…，πn由结合启发式规则的采样方法选择.采样方法选择时，首先利用启发式方法确定分配方向和分配工序.若存在多个优先等级相同工序，则以轮盘赌方法采样概率模型的Pi，j，k(i=πa，j=πa+1)得到工序πa+2.重复该过程能够生成问题的解.

（3）更新概率模型

设πk与πk-2，πk-1组合后产生的空闲时间为idtk.若idtk=0，则应用式（9）奖励若idtk＞0，则应用式（10）惩罚重复k=(3，4，…，n)能够学习生成解中三个连续工序的组合信息.

4.3.2 生成种群

在EEDA 中，种群大小设置为PS.种群中γ%个体从工作站j继续生成解，j为不满足快速判断方法时记录的工作站.其余个体从首个工作站生成解.生成种群过程如算法2.

4.4 局部搜索策略

生成种群后，首先采用针对主要目标的搜索策略，若该策略在连续三次种群迭代间未能更新CT，则采用针对次要目标的搜索策略.两种搜索策略的处理对象均为历史最优解.

4.4.1 针对主要目标的搜索策略

给定工作站数目和生产节拍，工序分配排列π1，π2，…，πn为满足约束的历史最优解.缩减生产节拍使πk分配至工作站j后生成非可行解.设πt为工作站j首个工序.考虑到工作站j之前的所有工作站已取得满足约束的部分解，为避免这种优质结构被破坏，随机地从πt，…，πk中选择工序插入其后工序来产生新解，并判断新解是否为可行解.该策略如图2所示.在每次启用时该策略执行10次.

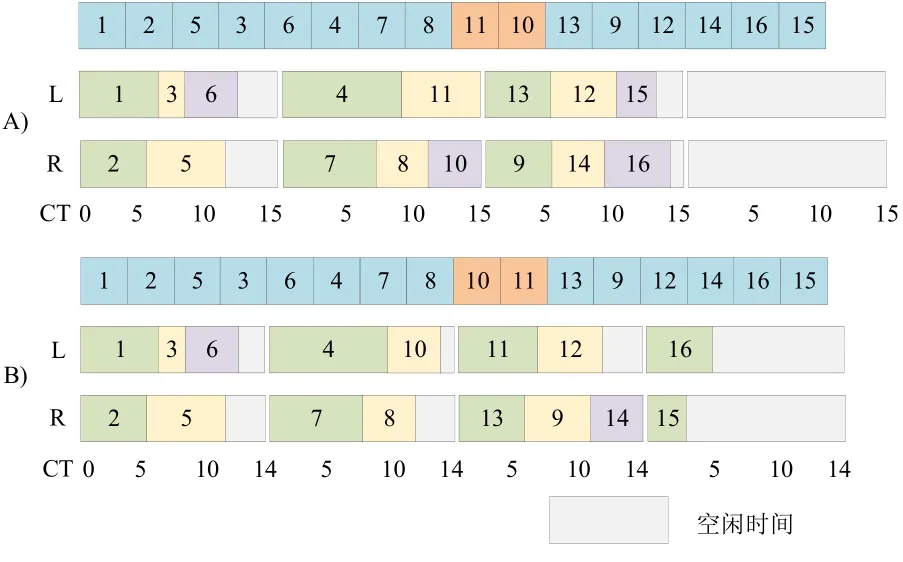
图2 针对CT的局部搜索示意图

4.4.2 针对次要目标的搜索策略

由式（5）可知，工作量偏差较大的工作站相比偏差较小的工作站存在更大的优化空间.因此，本策略针对偏差值最大工作站进行操作.如图3 所示，首先计算所有工作站两侧的偏差值，随机地从偏差值最大工作站中选取工序向后续工序做插入调整，然后判断新解是否为可行解及是否更新SI 且不降低CT.本搜索策略在每次启用时执行3次.

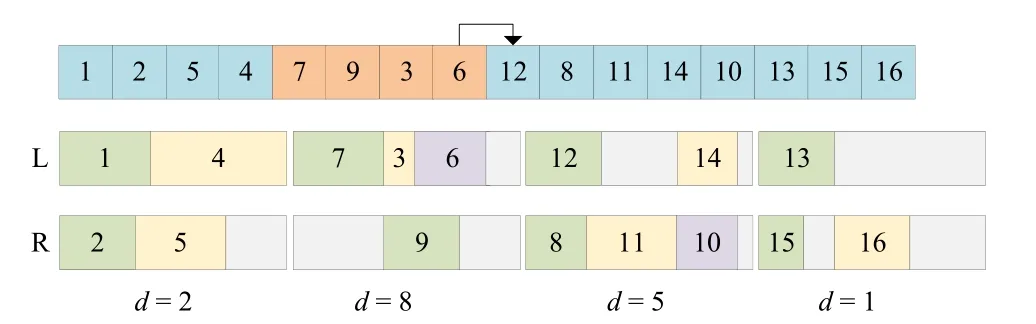
图3 针对SI的局部搜索示意图

5 实验分析与比较

实验中问题实例源于Kim 等［15，16］的研究.所有测试由Delphi7 编程实现.CPU 为2.33 GHz，内存为8 GB.每种算法单次实验的运行时间设置为n×n×15 毫秒.每种问题实例独立地进行20 次实验，取结果的平均值作比较.

5.1 参数设置

EEDA主要参数为种群规模PS、精英个体占比γ、奖励系数α和惩罚系数β.采用实验设计方法确定参数取值为PS=50，γ=0.5，α=0.7，β=0.3.

5.2 EEDA关键环节有效性验证

5.2.1 验证自适应策略生成初始CT有效性

表2为实验结果.CTDABC表示DABC 算法在相同时间内计算获取的CT.DABC 算法中参数设置方法为考虑不同结构特点的问题实例将起始CT 设置较大，导致算法自较高起点“自上而下”寻优，而EEDA中自适应策略采用“自下而上”的方式确立初始CT.在大规模问题实例上，只需百次左右迭代即可生成可行的初始CT.因此自适应策略在生成初始CT较参数设置方法有优势.

试验和实际使用表明：钻机车在坡度行驶时，可通过液力缓速器和发动机制动联合作用使车辆在下坡过程中选择合适档位，降低车速。具体过程如下：首先打开缓速器开关(液力缓速器功能激活)，操纵缓速器杆，它共有7个档位选择，制动强度依次增加，可根据下长坡路段的驾驶操控情况选择合适的制动档位，该操纵杆只有在松开油门的情况下才能起作用。

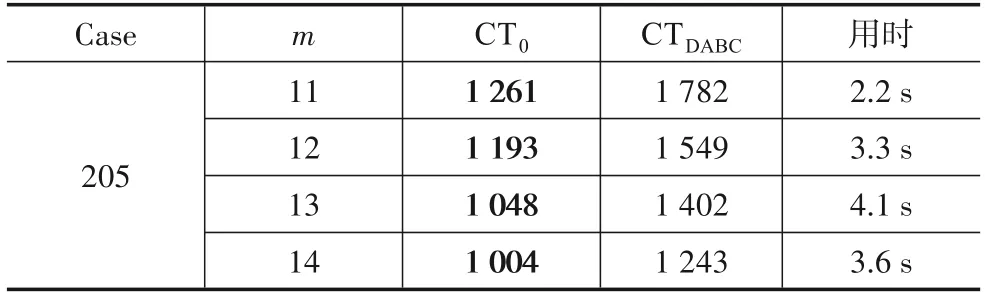
表2 大规模问题实例下初始CT设置方法的实验结果

5.2.2 验证结合启发式规则采样方法的有效性

将EEDA与其变体Rand_EEDA、Heuristic_EEDA进行实验比较，Rand_EEDA和Heuristic_EEDA 分别采用随机方法和启发式方法选择工序.表3 实验结果表明，Rand_EEDA、Heuristic_EEDA和EEDA 的性能依次增强.相比随机方法，由于启发式方法能从产生空闲时间最小工序集中随机选择工序，所以启发式方法能够生成较优解.而EEDA 利用概率模型从产生空闲时间最小工序集中选择工序，能够生成更为合理的工序排列，从而能获得更好的优质解.

表3 三种工序选择方法的实验结果

5.3 EEDA与其他算法对比

为进一步验证EEDA 性能，将EEDA 与求解TALBP-Ⅱ的有效算法DABC［3］、IG［4］和GA［15］对比.表4和图4 为实验结果.各算法在CT 指标上性能近似，但在SI 指标上EEDA 明显占优.其他比较算法仅在已有的进化算法框架或IG算法框架中加入一些通用搜索操作，故这些算法实际性能较为有限.EEDA 采用基于三维概率模型的EDA 算法框架，可合理学习优质解信息并避免其他比较算法存在的优质解模式破坏问题［17］，从而能更好地引导算法搜索方向.同时，EEDA 进一步考虑问题特性，设计并引入了新颖有效的新解生成方法、主次目标协同优化的局部搜索方法、可行解快速判断方法.这使EEDA 具有更强的搜索效率，故能在算法对比中明显占优.

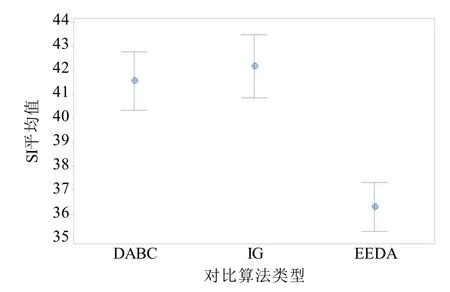
图4 对比算法实验结果的区间图比较

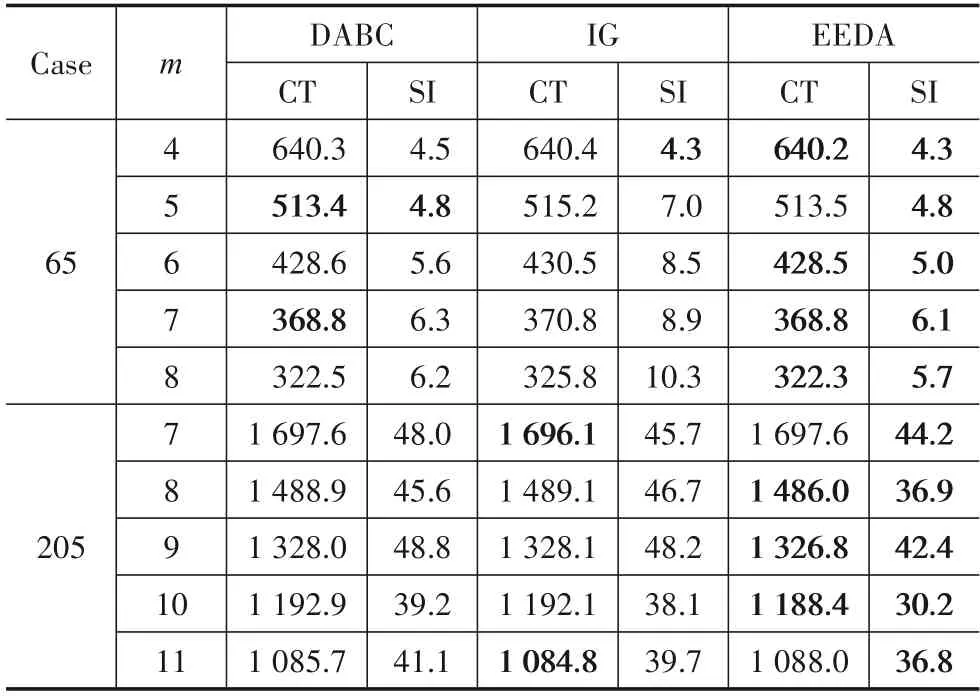
表4 各对比算法在各种问题实例下的实验结果

6 结论

针对双边装配线第二类平衡问题（TALBP-Ⅱ），将生产节拍（CT）和平滑指数（SI）作为主次优化目标，提出增强分布估计算法（EEDA）对TALBP-Ⅱ求解.具体结论如下：（1）采用自适应策略生成初始CT，可提升初始解质量；（2）设计结合启发式规则的采样方法，可提高生成优质解的概率；（3）利用主次目标协同优化的局部搜索方法，可增强算法局部搜索能力；（4）提出可行解快速判断方法，能缩短算法每代的运行时间从而提升算法搜索效率.