自适应非局部空间约束与K-L信息的模糊C-均值噪声图像分割算法

王小鹏，魏统艺，房 超，朱生阳

(兰州交通大学电子与信息工程学院，甘肃兰州 730070)

1 引言

模糊C-均值聚类(fuzzy C-means，FCM)算法[1-6]是一种典型的无监督聚类算法，因其不需要提前训练样本、算法结构简单和聚类效果好等优点被广泛应用于图像分割领域，但该算法没有考虑图像的空间信息，因此对噪声的鲁棒性较差，为此国内外学者提出了许多FCM变体算法[7-8].文献[9]考虑了中心像素以外的其他邻域像素，提出了带有空间限制的FCM 算法(FCM with spatial constraints，FCM-S)，第1次将图像的空间信息引入FCM目标函数之中，对噪声具有一定的鲁棒性，但该算法在每次迭代时都需要计算邻域像素与聚类中心的距离，计算复杂度较高.文献[10]提出了一种加强的FCM算法(enhanced FCM，EnFCM)，该算法将基于像素的聚类转化为基于直方图的聚类，使算法复杂度降低，虽然基于直方图的聚类算法运行速度较快，但很难将其推广到彩色图像之上，因为彩色图像的直方图数量和像素个数基本相等，使得基于直方图的彩色图像聚类算法复杂度增加.文献[11]提出一种基于超像素的快速FCM算法(superpixel-based fast FCM，SFFCM)，该算法通过超像素预分割，将传统基于单个像素的FCM聚类转化为基于超像素区域的FCM聚类，有效降低了算法的复杂度，同时实现了基于直方图的彩色图像分割，聚类效果较好.文献[12]提出一种模糊局部双邻域信息C-均值聚类算法(fuzzy local double neighborhood information C-means，FLDNICM)，该算法通过构造权衡加权模糊因子和先验概率函数，实现局部空间信息和光谱信息的自适应计算，使得算法的灵活性和鲁棒性提高.为了提高运算效率，文献[13]提出一种基于形态学重建和隶属度滤波的

(morphological reconstruction and membership filtering，FRFCM)FCM变体算法，该算法用隶属度滤波代替目标函数中的邻域像素与聚类中心的距离计算，简化了计算过程.文献[14]提出一种带有空间约束的偏差校正嵌入式FCM 算法(bias correction embedded

FCM with spatial constraint，BCEFCM-S)，该算法通过双边滤波确保估计偏差的平滑性，通过对隶属度的空间约束抑制噪声，提高算法鲁棒性.虽然基于局部信息的FCM算法对噪声具有一定的鲁棒性，但该类算法没有考虑图像的上下文信息，因此当图像被噪声污染严重时，算法鲁棒性下降.文献[15-16]利用隐马尔可夫模型，计算相邻像素之间的先验概率，并将其引入FCM目标函数之中，提高了算法的鲁棒性;虽然隐马尔可夫模型能有效描述相邻像素之间的信息，但该模型是基于假设，而且随着噪声密度的升高，中心像素周围的邻域像素也可能是噪声像素，因此考虑邻域像素以外的其他像素块有利于提高算法鲁棒性.文献[17-18]提出基于非局部空间信息的FCM算法(FCM with non-local spatial information，FCM-NLS)，该算法考虑了邻域像素以外的其他像素块，其算法鲁棒性显著提高，但该类算法将当前像素的估计值用图像中与其具有相似邻域结构的像素加权平均代替，导致算法复杂度较高，且当图像被噪声污染严重时，容易出现欠分割现象.针对该问题，文献[19-20]提出了快速自适应非局部加权与隶属度连接的FCM算法(fast and adaptive non-local fuzzy C-means with membership linking，FANFCM-M)和自适应局部和区域级信息的FCM 算法(fuzzy adaptive local and region-level information C-means，FALRCM)，FANFCM-M算法利用递归高斯滤波计算非局部信息，降低计算复杂度，FALRCM算法将局部空间信息与非局部空间信息结合，提高了算法的鲁棒性，解决了非局部空间信息的欠分割问题.

虽然上述算法对噪声具有一定的鲁棒性，但仍然存在以下问题:1)FANFCM-M和FALRCM在计算非局部空间信息时，搜索窗口和邻域窗口的半径均为固定值，而对于不同均质区域的像素应设置不同的窗口半径，因此如何自适应设置窗口半径，是一个需要解决的问题;2)分割的模糊化在FCM中也至关重要，而带有隶属均值模板的Kullback-Leibler(K-L)信息可以有效的减少模糊化，但均值模板忽略了邻域像素的上下文信息，鲁棒性较差;3)在选择原始图像和局部或非局部空间信息项约束参数时，上述算法均采用人工设定的方法，使得算法灵活性较低.

本文提出一种自适应非局部空间约束与K-L信息的模糊C-均值聚类算法用于噪声图像分割.首先，通过定义平滑度，设计自适应匹配函数，实现非局部空间信息项搜索窗口和邻域窗口的自适应计算，克服非局部空间信息窗口大小固定的问题;其次，将K-L信息添加到目标函数，利用隐马尔可夫模型计算图像像素的上下文信息，减少分割的模糊性;最后，利用原始图像和非局部空间信息项局部方差的绝对差和其倒数自适应约束原始图像和非局部空间信息项，实现约束项参数的自适应选择，提高算法的灵活性.

2 非局部空间信息

为提高FCM算法的鲁棒性，文献[17-18]在目标函数中引入非局部空间信息项，该空间信息项不仅考虑了邻域像素对中心像素的影响，同时考虑了除邻域像素块以外的具有相似邻域结构的其他像素块，因此能更加充分的挖掘图像的冗余信息，提高算法的鲁棒性.其非局部空间信息项表述为

其中:Rj为以像素yj为中心的S×S搜索窗口，M(yq)和M(yj)分别为以像素yq和像素yj为中心的l×l(l＜S)邻域窗口，Gauss[M(yq)-M(yj)]是标准差为σ4的[M(yq)-M(yj)]2高斯和，h为平滑程度参数.

3 本文算法

传统FCM算法对异常值(如噪声点和离群点)较为敏感，难以分割噪声图像.本文算法通过定义平滑度，设计自适应匹配函数，实现非局部空间信息项搜索窗口和邻域窗口的自适应计算，同时将K-L信息引入目标函数，利用隐马尔可夫模型减少分割的模糊性，最后根据原始图像和非局部空间信息项的局部方差，自适应约束原始图像和非局部空间信息项，提高算法的灵活性.

3.1 搜索窗口和邻域窗口的自适应计算

首先，图像X的平滑度定义为

其中:为以像素Xj为中心的r×r邻域，NR为该邻域的基数，多次实验表明，r取3得到的分割结果较好.由平滑度定义可知，δj大小取决于Xj与其r×r邻域像素的差值，差值越大，平滑度值越大.其次，针对具有不同平滑度的区域，设置不同的搜索窗口和邻域窗口:当区域的平滑度值较大时，说明该区域中邻域像素与中心像素的差值较大，该区域属于非均质区域，即区域被噪声污染严重或其他非噪声干扰导致区域的像素值发生改变，而非局部空间信息项中当前像素的像素值是用图像中与其具有相似邻域结构的像素的加权平均代替，因此在非均质区域对应设置较小的搜索窗口和较大的邻域窗口，保证算法能用较小的搜索步长遍历图像像素，同时用较大的邻域窗口使得中心像素受其邻域像素的影响较大，尽可能平滑噪声、保持图像的边缘和细节信息;当区域平滑度值较小时，表明区域中邻域像素与中心像素的差值较小，即区域较为平滑，因此设置较大的搜索窗口和较小的邻域窗口，使算法用较大的搜索步长遍历图像像素，加快处理速度，同时用较小的邻域半径使得中心像素受其邻域像素的影响较小，尽量保持原始图像的信息.为此，设计了两个自适应匹配函数lj和Sj，分别表示为

其中:表示向下取整运算，δmax为所有像素平滑度的最大值，lj为像素Xj的邻域窗口，Sj为像素Xj的搜索窗口.通过以上匹配函数，实现非局部空间信息项搜索窗口和邻域窗口的自适应计算，进而通过式(1)-(2)计算图像的非局部信息，并将其引入FCM目标函数之中，提高算法的鲁棒性.

3.2 基于隐马尔可夫模型的K-L信息

为了减少分割的模糊化，文献[21]将K-L信息作为正则项引入FCM目标函数之中，其表示为

隐马尔可夫模型作为经典的统计模型，用于图像分割时能充分考虑图像的上下文信息，因此本文利用隐马尔可夫模型计算图像的邻域信息，并用其代替原始K-L正则项中的均值运算，提高算法鲁棒性.隐马尔可夫模型的逐点先验概率表示为

其中:μ为基团参数，Eij为邻域能量函数，表示为

式中:∂j为以像素yj为中心的邻域范围，δ(·)为克罗内克函数

通过隐马尔可夫模型计算图像逐点的先验概率，并将其作为正则项引入到FCM目标函数之中，从而达到减少分割的模糊性、提高算法鲁棒性的目的.

为了说明本文提出的基于隐马尔可夫模型的K-L信息在噪声抑制能力和降低分割的模糊化方面均优于传统K-L信息，使用Gibbs采样器产生三幅不同的合成图像，并用5%的高斯噪声污染图像，然后分3种情况讨论两种算法的性能.在图1-3中，(a)为噪声图像，(b)为用红色矩形框标记的区域的像素值，其中灰色背景的为噪声像素，(c)为本文算法分割的最终结果，(d)为用文献[21]分割后的3个聚类簇的隶属度值，(e)为本文算法分割后的3个聚类簇的隶属度值.

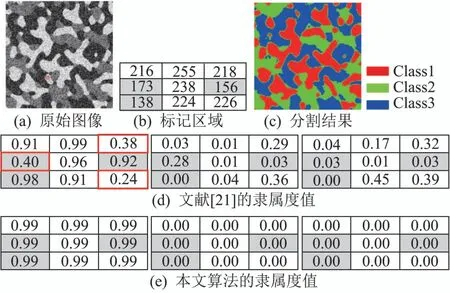
图1 中心像素不含噪声Fig.1 No noise in the center pixel

情况1区域的中心像素没有噪声，它的邻域像素被噪声污染.图1(a)中标记的3×3区域的像素值如图1(b)所示，图中的噪声像素的灰度值分别为173，138和156，与中心像素的灰度值(238)相差较大.文献[21]和本文算法分别在第36次和第9次迭代后收敛，理论上，迭代后属于某一类的隶属度值应大于0.5，但基于传统K-L信息的FCM算法在迭代后，有1个噪声像素和2个非噪声像素的隶属度值小于0.5(如红色矩形框标记所示)，说明传统K-L信息难以分割被噪声污染严重的图像，无法很好的解决分割的模糊化，而本文算法在迭代完成之后，所有像素的隶属度值均大于0.99，说明本文算法能有效解决分割的模糊化，较好的实现像素聚类.

情况2区域的中心像素被噪声污染，它的邻域像素没有噪声.该情况中，中心噪声像素的灰度值为0，与其邻域像素相差较大.文献[21]和本文算法分别在第30次和第8次迭代后收敛，如图2(d)-(e)所示，基于传统K-L信息的FCM算法在迭代后，有3个像素出现误分类，其中中心噪声像素也未能正确分类，而本文算法的最终隶属度值均大于0.99，说明在此情况下，本文算法具有同样的噪声抑制能力和去模糊化能力.

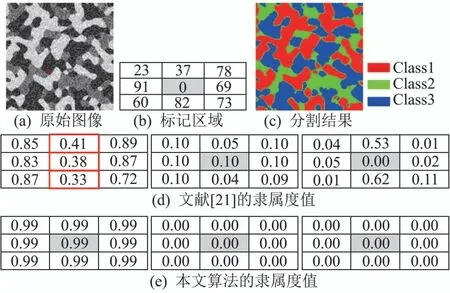
图2 中心像素为噪声像素Fig.2 The center pixel is a noisy pixel

情况3在情况1和2中，给定的局部窗口的像素是同质的，即像素属于同一区域，事实上，也有一些像素位于物体的边界上，如图3所示，图3(b)显示了两个区域的像素(黑色背景区域为第1类像素，白色背景区域为第2类像素，噪声像素背景为灰色).文献[21]和本文算法分别在第45次和第15次迭代后收敛，如图3(d)-(e)所示，基于传统K-L信息的FCM算法在迭代后，有4个像素未能正确分类，而本文算法的最终隶属度值均大于0.5，说明本文算法能较好的分割噪声图像，同时保持图像的边缘信息.

图3 像素位于物体的边界上Fig.3 Pixels are located on the boundary of the object

3.3 本文算法目标函数

为了自适应计算非局部空间信息项的搜索窗口和邻域窗口，有效减少分割的模糊化，提出一种自适应非局部空间约束与K-L信息的模糊C-均值噪声图像分割算法，目标函数为

其中:αj和βj为原始图像和非局部空间信息项的权值，为非局部空间信息项的第j个像素的像素值，为像素邻域范围内的先验概率.对于噪声图像，当图像被噪声污染严重时，应当设置较大的βj和较小的αj，使得非局部空间信息项主要影响分割结果;当图像噪声较小时，原始图像应占主要权值，从而保持图像细节信息，因此αj应足够大而βj应尽可能小.本文利用原始图像和非局部空间信息项的局部方差，自适应计算其权值，提高算法的灵活性.

对于图像数据，其局部方差反映了图像的局部均匀程度，局部方差越小，则图像越平滑，被噪声污染越轻，反之，图像被噪声污染越严重，因此有

本文算法详细步骤如下:

步骤1输入参数，包括聚类数目K，最小误差ε，最大迭代次数T，高斯函数平滑参数h，正则项控制参数γ;

步骤2利用式(3)计算每个像素的平滑度;

步骤3利用式(4)-(5)自适应计算非局部空间信息的搜索窗口和邻域窗口;

步骤4计算非局部空间信息项

步骤5利用式(12)计算αj和βj;

步骤6初始化隶属度矩阵，并令a1;

步骤7利用隶属度为图像分配初始标签;

步骤8利用式(8)计算像素点的先验概率;

步骤9利用式(14)计算聚类中心

步骤10利用式(13)计算隶属度

步骤11利用式(11)计算目标函数

步骤12判断≤ε是否成立，若是则退出迭代，若否则返回步骤8;

步骤13将每个像素分类到隶属度最大的聚类簇中，完成图像分割.

4 实验结果与分析

为了验证算法的有效性，采用含噪合成图像以及BSDS500[22]，AID[23]和MSRC[24]数据库的彩色图像进行测试，并将实验结果与FCM[6]，FCM-NLS[17]，FRFCM[13]和FANFCM-M[19]进行对比.为了模拟真实环境的噪声情况，本文采用等量高斯白噪声、椒盐噪声以及乘性噪声的混合噪声污染图像，并通过改变混合噪声密度控制图像被噪声污染的程度.分割性能指标采用分割精准度(segmentation accuracy，SA)、平均交互比(mean intersection over union，mIoU)、归一化互信息(normalized mutual information，NMI)、模糊分割系数(fuzzy partition coefficient，VPC)和模糊分割熵(fuzzy partition entropy，VPE)

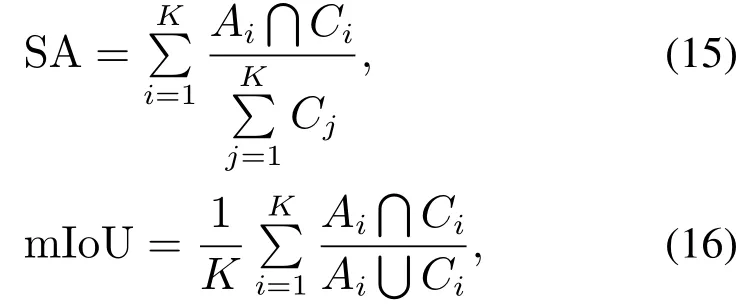
其中:Ai为分割结果中第i个聚类簇的像素集合，Ci为参考图像中第i个聚类簇的像素集合，SA与mIoU越大，分割性能越好.对于灰度图像I1和I2

其中:MI(I1，I2)为图像I1和I2的互信息，H(I1)和H(I2)分别表示图像I1和I2的熵，NMI越大，分割结果越好.模糊分割系数和模糊分割熵定义为

VPC越大分割效果越好，VPE越小分割效果越好.

4.1 合成图像分割实验

为了测试算法性能，选取3幅人工合成图像进行实验，其大小均为256×256，分别加入等量的密度为5%，10%，15%和20%的混合噪声，分割结果如图4所示，分割指标如表1所示.

图4 5种算法对三幅合成图像的分割结果Fig.4 Segmentation results of 5 algorithms for three synthetic images

视觉效果上，传统FCM的分割效果最差，结果中含有大量的噪声;FCM-NLS在分割合成图像1和3时存在欠分割现象，结果中存在少量噪声，因此视觉效果较差;FRFCM对合成图像1和3的分割效果较好，但在边缘处存在少量的噪声斑点，而对合成图像2的分割效果较差，结果中存在大量噪声;FANFCM-M可以对3幅合成图像进行较好的分割，但在合成图像2的结果中存在少量噪声斑点，导致视觉效果较差;本文算法在视觉效果上优于其他几种比较算法，且能对3幅合成图像进行精准的分割.

在性能指标上，各种算法的分割指标随着混合噪声密度的升高而降低.4种比较算法中，FANFCM-M算法在SA，NMI和VPC上表现得最好，而在mIoU和VPE指标上效果最好的为FRFCM算法，本文算法在各种性能指标上均优于其他几种比较算法，值得注意的是，本文算法的VPC和VPE分别达到99.92%和0.14%，分割性能显著提升.

4.2 彩色图像分割实验

上一节的数值结果表明，本文算法对噪声合成图像有较好的分割性能，为了测试本文算法对噪声彩色图像的分割性能，本节对不同数据库的彩色图像进行了2次实验.

实验1首先对BSDS500数据库中的所有彩色图像进行实验，各种算法的平均性能指标如表2所示，为了展示各个算法的分割结果，选取7幅具有代表性的图像进行视觉效果分析，分割结果如图5所示.其中:FCM算法的分割结果中存在大量噪声，视觉效果较差;FCM-NLS 对#3063，#42049和#241004图像的分割结果较好，基本能有效地分割目标，但#86016，#100007和#24063的结果中存在严重的过分割现象，导致视觉效果较差;FRFCM结果中图像#42049的分割结果边缘轮廓清晰、细节保持较好，但在其他图像的分割结果中出现严重的误分割现象，几乎不能分割图像的主要目标和背景，因此视觉效果最差;FANFCM-M对#3063同样存在误分割现象，将飞机和白云误分割为一类，在图像#3096，#24063和#241004的结果中，存在大量的噪声斑点，说明FANFCM-M对噪声的抑制能力有限，在#36016和#100007的结果中存在过分割现象，导致视觉效果较差;本文算法对7幅图像均能进行有效的分割，视觉效果较好.各种算法的平均性能指标显示，本文算法在各个指标上均优于其他几种比较算法，说明本文算法能精准分割噪声图像.

图5 5种算法对BSDS500数据库的图像分割结果Fig.5 Image segmentation results of 5 algorithms on BSDS500 database

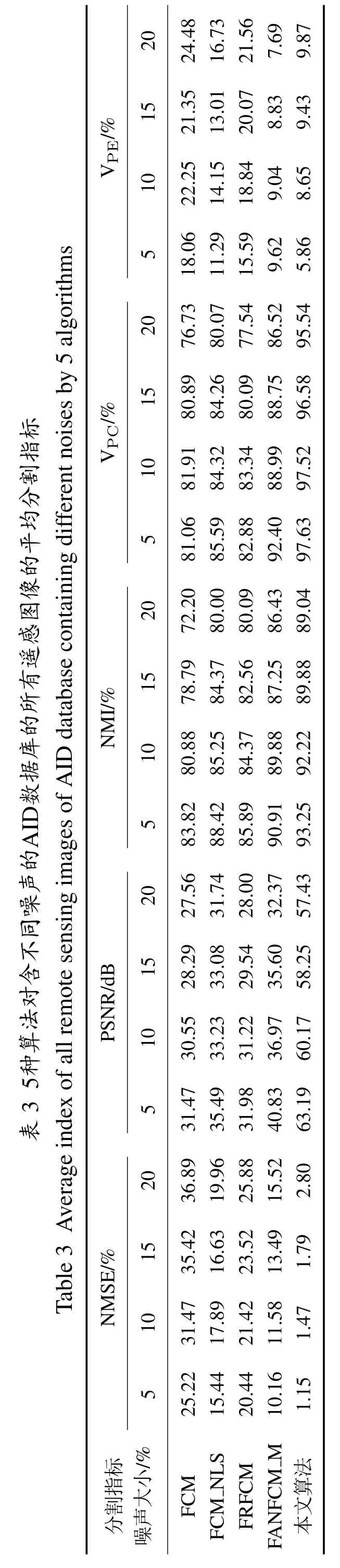
实验2其次，本文对AID数据库中30个类别的遥感图像和MSRC数据库中19个类别的目标识别彩色图像进行了相同实验，各个算法的平均性能指标如表3-4所示，由于AID和MSRC数据库没有对应的真值图，因此本节所选用的评价指标为:归一化均方误差(normalized mean square error，NMSE)、峰值信噪比(peak signal-to-noise ratio，PSNR)，NMI，VPC和VPE，图6-7为本文算法对含噪的遥感图像和目标识别图像的分割结果，其中:NMSE和PSNR的计算公式为

图6 本文算法对AID数据库的图像分割结果Fig.6 The image segmentation results of the algorithm in the AID database

其中:M和N分别为图像的宽和高，I(i，j)为原始图像，I′(i，j)为分割后的图像，NMSE越小，分割效果越好，PSNR越大，分割效果越好.表3和表4数值结果显示，5种算方法中，FCM的分割精度最低，主要原因是原始FCM算法没有考虑图像的空间信息，因此对噪声较为敏感;FCM-NLS 和FRFCM 算法相较于原始FCM，分割性能有所提升;FANFCM-M的分割性能接近本文算法，主要是因为该算法也是基于非局部空间信息的FCM变体算法，因此鲁棒性较好;本文算法将非局部空间信息引入FCM目标函数，实现了窗口的自适应计算，考虑了图像的上下文信息，因此鲁棒性更好，分割精度更高;与AID数据库相比，各种算法在MSRC数据库的分割精度更高，这是因为AID数据库中的遥感图像目标较小、地物类型相对复杂，因此分割精度较低.

4.3 复杂度分析

复杂度是评价算法性能的重要因素，由于编程思想不同，准确的复杂度是很难获取的，因此，对于聚类过程，可计算每种方法的目标函数的计算复杂度.各种算法的计算复杂度和分割BSDS500数据库的平均时间复杂度如表5所示.

在表5中，N为图像的像素个数，K为聚类数目，a为迭代次数，Q为灰度级数，S和l分别为搜索窗口半径和邻域窗口半径.计算复杂度最低的为FCM和FANFCM-M，由于FANFCM-M将逐像素循环修改为搜索区域逐像素循环，因此复杂度从O(n5)降到O(n3);而FCM-NLS算法采用原始的非局部空间信息，因此复杂度为O(n5);FRFCM在形态学重构过程中，使用邻域搜索，因此复杂度为O(n4);本文算法的复杂度虽然为O(n5)，但各个窗口的大小都是自适应计算的，因此鲁棒性较好，而且随着近几年GPU的发展，利用GPU将串行计算改为并行计算，可以节省一些时间，因此本文算法可以应用在不同的图像分割场景.而从时间复杂度来看，传统FCM 算法的运行时间最短，FCM NLS的运行时间最长，主要原因是非局部空间信息在运算过程中，需要将图像分为若干个像素块运算，因此计算成本较高;而本文算法由于实现了搜索窗口和邻域窗口的自适应计算，且引入了基于隐马尔可夫的K-L正则项，因此使得算法的模糊化降低，进而使得迭代步数减少，因此运行时间较快.

5 结束语

提出了一种自适应非局部空间约束与K-L信息的模糊C-均值噪声图像分割算法.针对传统FCM算法对异常值较为敏感，难以分割噪声图像的问题，考虑了图像的非局部空间信息，提出了一种基于匹配函数的非局部信息窗口自适应计算方法和基于局部方差的原始图像和非局部空间信息项自适应加权方法，实现了搜索窗口和邻域窗口的自适应计算，提高了FCM抗噪性;同时将K-L信息引入FCM目标函数，并用隐马尔可夫模型计算图像的上下文信息，减少分割的模糊性.通过含噪的合成图像和彩色图像实验，相比于FCM-NLS 算法、FRFCM算法和FANFCM-M算法，本文算法的抗噪声性能更强，分割精度更高.而本文算法的计算复杂度较高，如何降低复杂度将是下一步的研究目标.

图7 本文算法对MSRC数据库的图像分割结果Fig.7 The image segmentation results of the algorithm in the MSRC database