质子交换膜燃料电池模型的频域分数阶子空间辨识

叶伟琴，戚志东，田家欣，孙成硕

(南京理工大学自动化学院，江苏南京 210094)

1 引言

质子交换膜燃料电池(proton exchange membrane fuel cell，PEMFC)是一种清洁、高效的氢燃料电池，具有启动温度低、功率密度高、响应速度快、效率高等突出优点[1].PEMFC发电过程包括流动、传热、传质和电化学反应等多种物理化学现象，具有典型的分数阶特性[2-3].建立准确的电特性模型是对其进行电特性控制研究的基础.

近年来，不少研究人员对PEMFC的电特性建模作出了相应探索，建模方法分为机理建模和辨识建模，机理建模过程复杂、模型参数众多且获取难度大，因此考虑辨识建模.然而，经典的辨识方法在处理多变量系统辨识方面具有局限性和不足，考虑到辨识算法的实用性、计算量、收敛性等问题，子空间辨识方法是最合适的选择[4].如Sami等人[5]采用子空间辨识方法建立了PEMFC/超级电容混合供电系统的状态空间模型，用于研发一种动态响应速度快、可持续发电的高效电源管理单元.徐夏吟[6]采用多变量输出误差状态方 程(multivariable output error state space，MOESP)子空间辨识算法建立了PEMFC温度与冷却水流量之间的状态空间模型，该模型可以很好地描述PEMFC的温度动态特性.

研究表明，PEMFC发电过程中气体扩散[7]、对流扩散[8]、热量传导[9]以及电化学反应等动态过程均存在分数阶特性.为此，一些研究人员在建模方法中加入分数阶微积分理论，以求更加准确地描述PEMFC的动态特性.Taleb[8]建立了PEMFC分数阶等效电路模型.Leng等人[10]和Qi等人[9]采用分数阶微分方程描述PEMFC反应气体扩散的动态过程，能更加精确的刻画PEMFC内部的气体扩散现象.胡聪[11]采用分数阶子空间辨识方法建立了空冷型PEMFC的分数阶状态空间模型(fractional order state space，FOSS)，但没有采用全局优化算法对辨识算法中较多的未知参数进行寻优.戈卫平[12]采用时域分数阶子空间辨识方法建立了PEMFC分数阶电特性模型，该辨识方法得到的模型能够较好的描述PEMFC的电特性.但上述方法都是基于时域，计算时域信号的分数阶导数时，存在较大的计算复杂度.目前用频域分数阶子空间辨识建立PEMFC电特性模型的研究较少.本文考虑将计算从时域转换到频域，时域中的微分将在频域中转化为乘积的形式.此外，只要覆盖系统的带宽，频域辨识算法所需的数据量也较少，这些优点使得频域子空间辨识方法在分数阶系统的辨识中具有更大的优势.

本文考虑到质子交换膜燃料电池PEMFC系统发电过程中的分数阶特性，将分数阶微积分理论与频域子空间辨识结合，提出一种频域分数阶子空间辨识方法建立PEMFC的FOSS.为了得到输入输出的频率响应数据，采用随机多频正弦激励信号对时域采集的信号进行处理;构造实、虚部矩阵，通过RQ分解、SVD分解以及最小二乘法求解系统系数矩阵.考虑到频域分数阶子空间辨识过程中，存在多个未知参数，本文将粒子群算法(particle swarm optimizatio，PSO)作为主线，加入遗传算法(genetic algorithm，GA)中的选择、交叉和变异操作，提出了一种遗传-粒子群GAPSO混合优化算法对参数进行寻优，以获得更加准确的PEMFC的电特性FOSS模型.

2 PEMFC

PEMFC是一个复杂系统，其发电过程包含有气体扩散、质子传输、电化学以及热量耗散等物理、化学过程.空冷型PEMFC测控系统的结构如图1所示.氢气进入PEMFC电堆与氧气发生还原反应生成水、热量和电能;风扇负责带来电化学反应所需的氧气并对电堆进行散热;排气阀负责排出水和多余的氢气;测控系统通过采集负载电流、氢气流量、氢气压力、输出电压、输出功率、电堆温度、环境温度等变量的电信号传送给控制器，进而调节风扇电压、氢气流量对PEMFC的发电性能进行调控.

图1 空冷型PEMFC测控系统结构图Fig.1 Structure diagram of air cooled PEMFC measurement and control system

PEMFC是一个典型的多输入多输出系统，影响PEMFC发电过程的因素有气体流量、气体压力、堆温、湿度和负载电流等，为了减小建模复杂度，本文采用文献[13]中的典型相关分析法[13]选取与PEMFC电特性相关性最大的输入变量，并采用相关性分析去除冗余输入变量.最终选取氢气流量和负载电流作为输入变量，输出电压和功率作为输出变量.

3 频域分数阶子空间辨识方法

子空间辨识方法可以分为时域和频域，但是在计算时域信号的分数阶导数时，存在较大的计算复杂度.而频域辨识方法能够将时域中的微分将在频域中转化为乘积的形式，此外，只要覆盖系统的带宽，频域辨识算法所需的数据量也较少.

3.1 问题描述

线性时不变分数阶系统的分数阶状态空间方程为

其 中:A ∈Rn×n，B ∈Rn×m，C ∈Rl×n，D ∈Rl×m为常数未知矩阵，需要通过辨识得到，α是微积分阶次，Dα为微积分的操作算子，n为系统矩阵A维数，u(t)∈Rm为输入变量，y(t)∈Rl为输出变量，m为输入变量个数，l为输出变量个数.假定系统是稳定且可观测的，系统系数矩阵A的维数已知.

本文选取Caputo 定义作为理论推导的基础[14]，Caputo定义的分数阶微积分表达式如下:

其中:a和t表示微积分的上下限，Γ(·)为Gamma函数，m-1 ≤α ＜m，m ∈N，其Laplace变换为

借助分数阶微积分的Laplace变换，可以得到系数矩阵与传递函数的关系如下:

其中n为系统矩阵A维数.

3.2 频域分数阶子空间辨识

3.2.1 激励信号

在进行频域子空间辨识之前，首先需要从时域采样的数据中获得频率响应函数(frequency response function，FRF).一般情况下，用于系统辨识的激励信号需要满足一些激励条件，即用于辨识的信号需要足够的带宽相对于被辨识的系统，可用的输入信号有白噪声、伪随机二进制序列、多频正弦等[15].对于FRF[16]的测量，需要选择合适的激励信号，除了具有足够的频谱宽度外，还应该具有较小的峰值因子/时间因子[16].本文采用的是多频正弦激励信号.多频正弦是一组正弦谐波信号的和，其表达式如下:

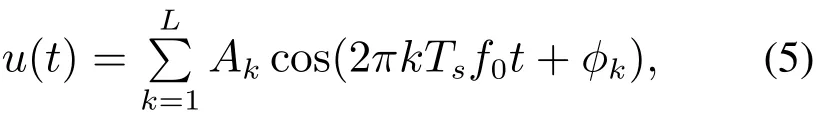
其中:Ts是采样周期，f0是基频，根据相位可以选择多频正弦的形式，不同的多频正弦形式φk不同，本文选择随机多频正弦:φk～U(0，2π)，U(0，2π)表示在区间(0，2π)内均匀分布.

当获得输入输出数据后，使用以下公式直接从时域信号中获得FRF:

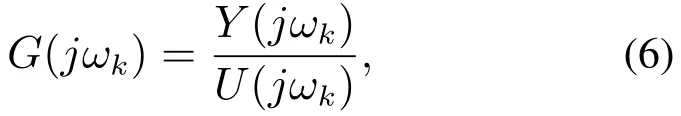
其中Y(jωk)可以通过离散傅里叶变换获得，公式如下:

其中N表示采样点个数，U(jωk)通过同样的方式定义.由于这些直接使用的时域信号不是稳态响应，因此这种方法不能产生可靠的频域数据.

为了获得准确的无频谱泄漏误差的FRF，需要对系统进行特殊的激励信号处理.本文采用的方法是利用整数周期的u(t)，如图2所示，这表示整个激励信号u(tall)包括几个完整的信号，即u(t)，u[1](t)，u[2](t)，···，u[i](t).然后，每一个输入周期都对应一个输出周期，最后一个输出周期y[i](t)对应的u[i](t)可以看作是相对准确的稳态响应.最后，利用时域中的这部分信号，通过计算式(5)-(6)得到FRF.

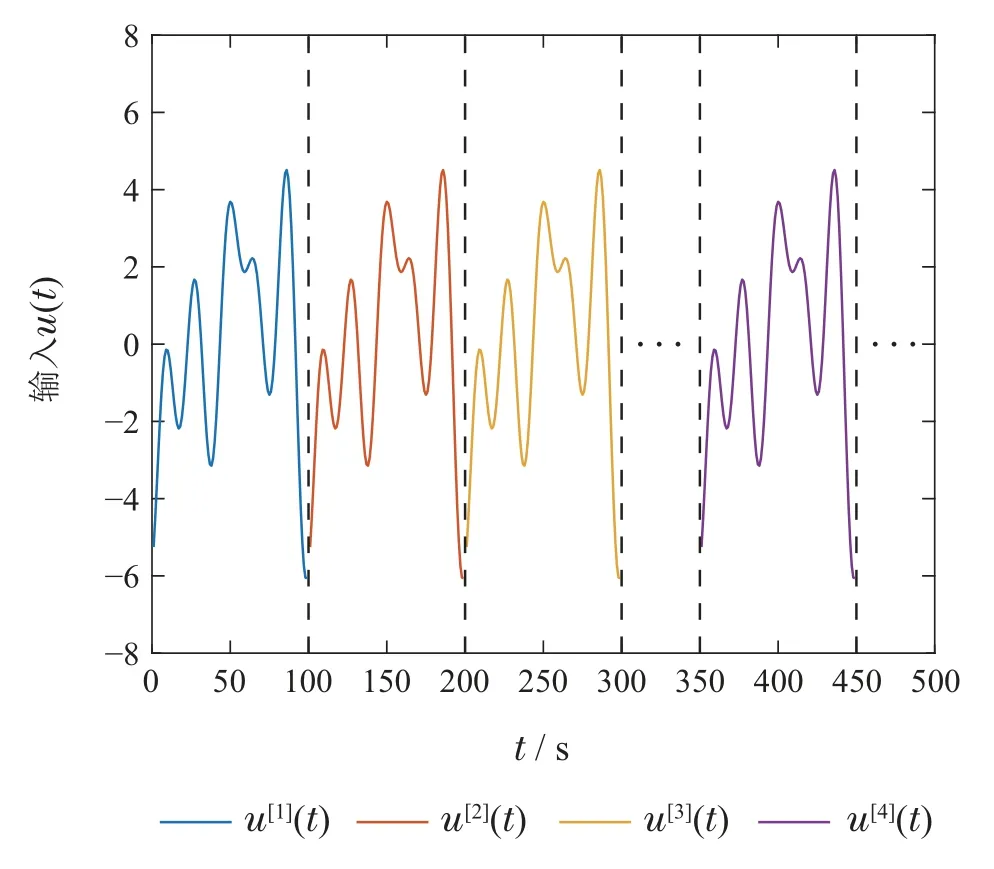
图2 周期性多频正弦激励信号示意图Fig.2 Schematic diagram of periodic multi-frequency sinusoidal excitation signal

利用设计的周期性激励信号得到输入输出数据的FRF后，开始进行频域分数阶子空间辨识过程，最后期望得到一个FOSS模型.

3.2.2 系统系数矩阵辨识

1) 将时域模型转换到频域模型.

首先，通过Laplace变换，将分数阶系统模型转换到s域，令sjω，可得

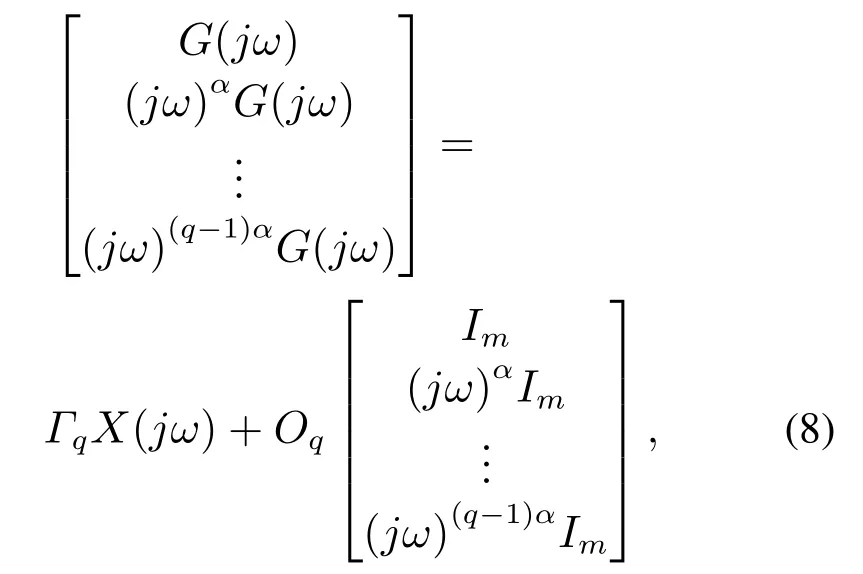
其中q是一个辅助阶次，表示扩展可观测矩阵的行数，且满足条件q≥n，其矩阵构成为

且Oq为下三角Toeplitz矩阵，其矩阵构成为

对于式(8)中所有的ω，都是使用不同采样频率ωk下的采样数据，其中k1，2，···，M，这M个向量可以被合并为

其中G表示为

Gk表示为

引入术语Gre，定义如下:

3) 对R22进行SVD分解

其中Σ+的对角线元素是R22的非零奇异值，且Σ+的选择取决于系统矩阵A的维数.

5) 计算矩阵A和C

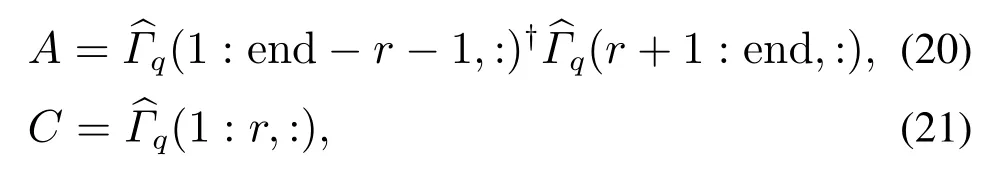
其中符号†表示矩阵的广义逆.

6) 用最小二乘法计算矩阵B和D

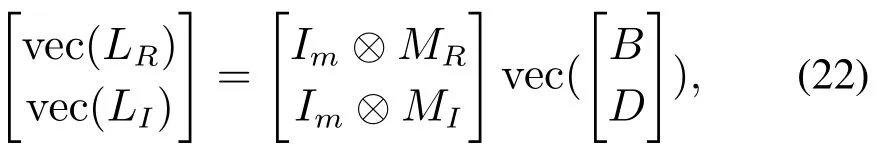
其中:⊗是Kronecker积，vec(·)表示将矩阵的每一列合并排成一列，且有

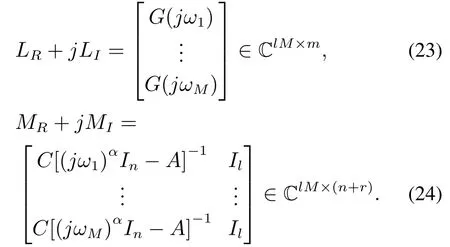
3.2.3 未知参数优化

在上述辨识过程中，同元分数阶次α(0＜α ＜2)、辅助阶次q(2＜q ＜10)以及频域采样点数M(2＜M＜20)未知的，因此需采用优化算法对参数进行优化.本文将GA和PSO算法结合起来，提出GA-PSO混合优化算法，将PSO算法作为主线，其中加入GA中的选择、交叉和变异操作，以进一步提高种群中个体的自适应调整搜索方向、增强全局寻优的能力.GA-PSO混合优化算法具体步骤如下:

1) 初始化GA-PSO混合优化算法中的粒子种群和参数;

2) 根据构造的适应度函数，计算每个粒子的适应度值，将每个粒子作为粒子组中当前种群的局部最优粒子，记为Ppbest，将适应度最好的粒子作为全局种群中的全局最优粒子，记为Pgbest;

3) 设置当前迭代次数为g，根据以下公式更新粒子的速度和位置;

4) 从均匀分布U(0，1)中选取随机数，判断其是否大于预设的阈值，若满足条件，则对种群进行编码，并执行种群的选择、交叉、变异操作，否则，将粒子的速度归零，位置保持不变，跳过该步骤;

5) 重新计算粒子的适应度值，将当前粒子组中适应度最好的粒子作为局部最优，记为Gpbest，将粒子群中适应度最好的粒子作为全局最优，记为Ggbest;

6) 比较Ppbest和Gpbest选出局部最优粒子记为Gpbest，比较Pgbest和Ggbest选出全局最优粒子记为Ggbest;

7) 根据式(25)-(26)更新粒子的速度和位置，判断是否满足算法终止条件，即当前迭代次数达到最大进化代数或粒子群的适应度值满足优化目标，若未满足终止条件则令迭代次数gg+1并返回步骤2)，直到满足终止条件，输出粒子群的全局最优解Ggbest即为待优化问题的最优解.

为了对上述提出的GA-PSO混合优化算法的寻优性能进行评估，与GA、PSO算法进行寻优性能的对比仿真测试.选取4个常用的标准测试函数作为优化对象，其表达式如下:

1) Sphere函数，如式(27)所示:

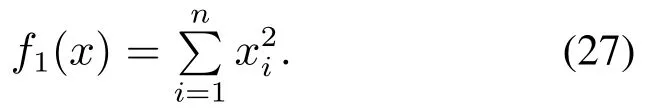
2) Ackley函数，如式(28)所示:

3) Rastrigin函数，如式(29)所示:

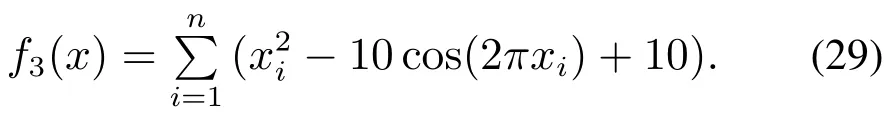
4) Griewank函数，如式(30)所示:

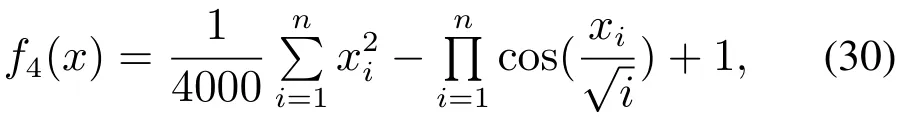
其中Sphere函数是简单的单峰值函数，而Ackley函数、Rastrigin函数以及Griewank函数是含有许多局部最优值的多峰值函数，可以用来测试优化算法的全局收敛性能和寻优精度.

标准测试函数的优化参数设置:维数为10，种群规模为100，适应度函数为测试函数本身，最优值为0，最大进化代数为500，学习因子c1的变化范围为[1，2.5]，学习因子c2的变化范围为[1.5，2.75]，惯性权重的变化范围为[0.4，0.9].Sphere函数的取值范围为[-10，10]，Ackley函数的取值范围为[-40，40]，Rastrigin函数的取值范围为[-5.12，5.12]，Griewank函数的取值范围为[-600，600].3种优化算法对4种标准测试函数的寻优曲线图如图3所示.

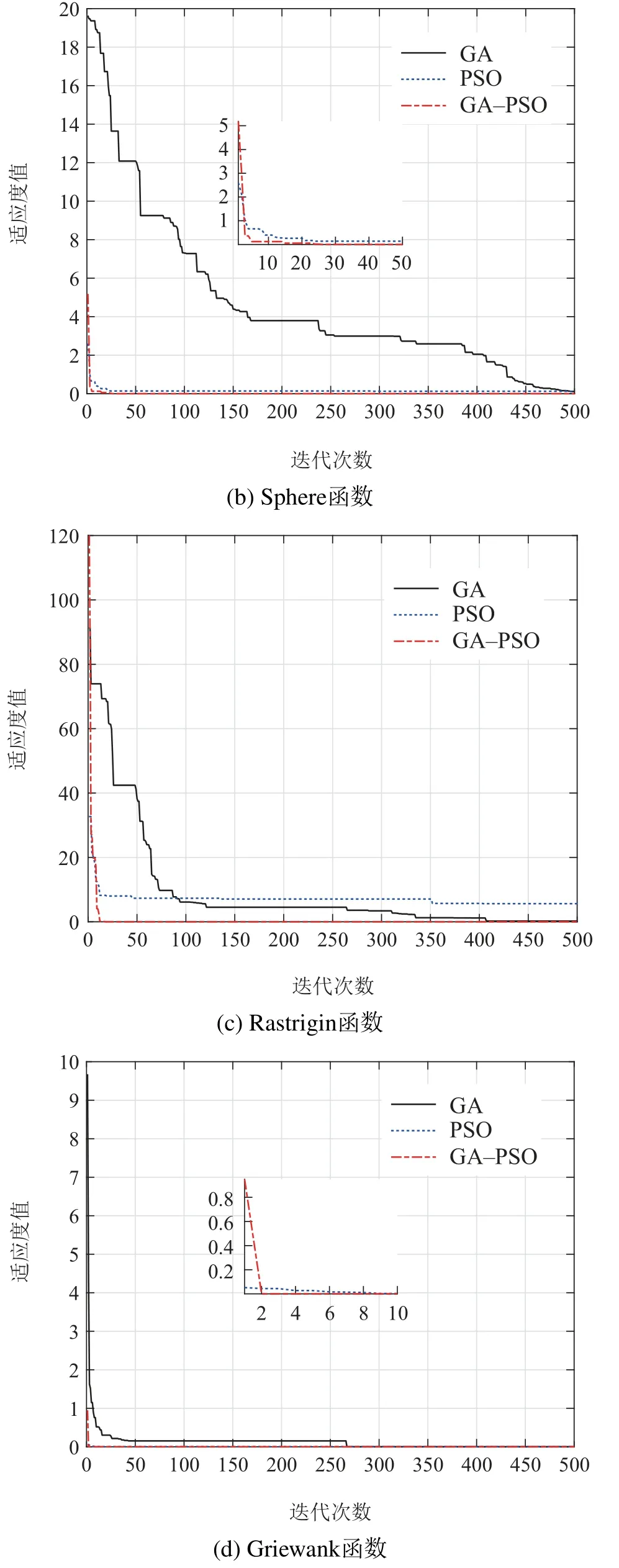
图3 适应度函数的寻优曲线Fig.3 Optimization curves of fitness functions

如图3，对于单峰值的Sphere函数，GA的搜索速度较慢，PSO的收敛精度不足，而GA-PSO混合优化算法的收敛速度和收敛精度都很高;对于存在多个局部极值的多峰函数Ackley 函数、Rastrigin 函数以及Griewank函数，PSO寻优时很容易陷入局部最优解，收敛精度和寻优成功率都很低;而GA-PSO混合优化算法的寻优成功率很高，这是因为该算法含有交叉、变异操作，能够帮助粒子跳出局部最优解，并收敛于全局最优解.

综上所述，分数阶系统的FOSS模型辨识的流程图如图4所示.

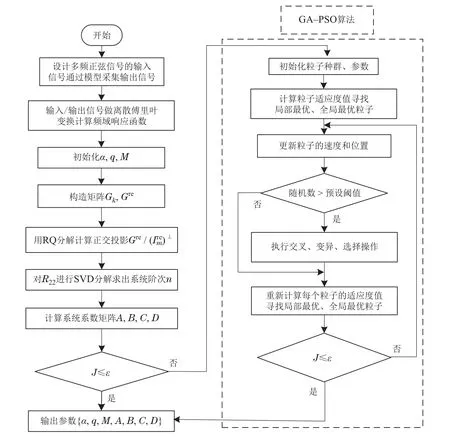
图4 分数阶系统的FOSS模型辨识流程图Fig.4 FOSS model identification flow chart of fractional order system

设置同元分数阶次、辅助阶次、频域采样点数的初始值，得到系统的系数矩阵后，将预测输出与实际输出的差值作为目标函数，判断其是否小于等于容许误差，即≤ε;若满足上述条件，则辨识结束;若不满足则需用优化算法对分数阶次进行寻优.定义目标函数如下:

转化为一个非线性优化问题:

4 PEMFC电特性FOSS模型

4.1 采集时域输入/输出数据，设计输入激励信号

为PEMFC的输入变量负载电流和氢气流量设计周期性多频正弦信号作为激励信号.输入信号为随机相位的多频正弦，系统由5个周期的输入信号激励，选择采样频率fs5 Hz，频谱分辨率f00.05 Hz，则采样间隔Ts1/fs0.2 s，测量采集输入/输出信号N100个点对应一个激励周期.输入u(t)和输出y(t)信号曲线如图5-6所示.

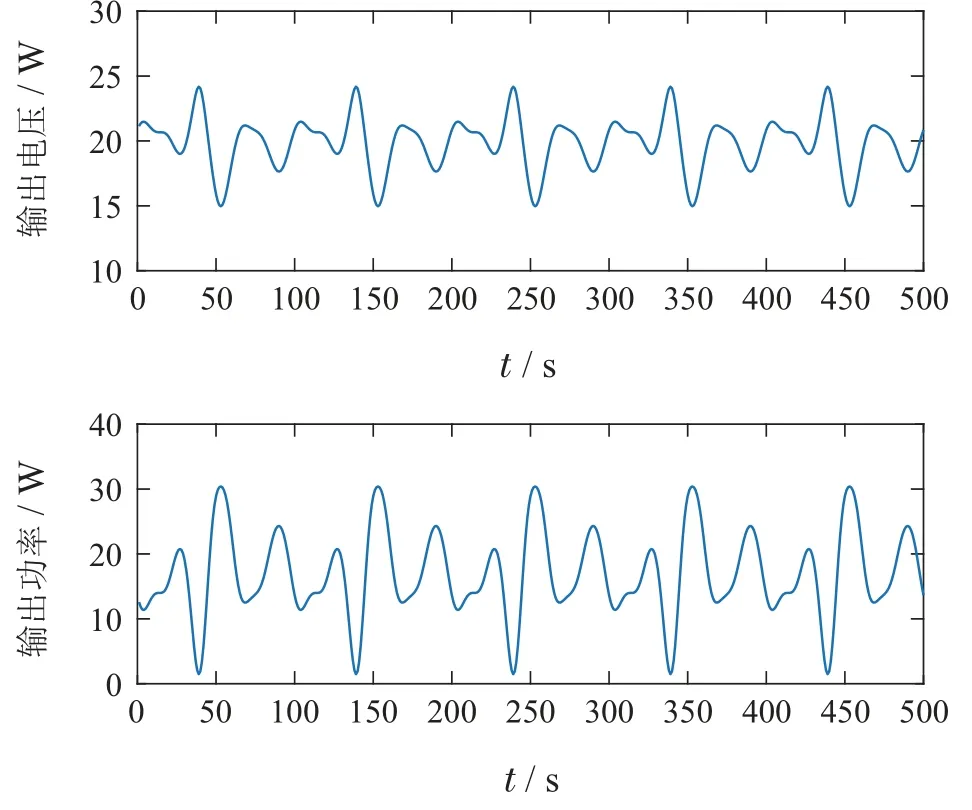
图5 负载电流和氢气流量的周期性多频正弦激励信号Fig.5 Periodic multi-frequency sinusoidal excitation signal of load current and hydrogen flow

4.2 获取频域数据，计算FRF

对最后一个周期的输入/输出时域信号按照式(3)作离散傅里叶变换，得到频域数据U(jωk)和Y(jωk).然后按照式(6)求得系统的FRF，即G(jωk)矩阵.

图6 PEMFC系统输出电压和功率Fig.6 Output voltage and power curve of PEMFC system

4.3 频域分数阶子空间辨识

设置初始值，迭代次数i0，同元分数阶次α0.9，辅助阶次q5，频域采样点数M7.系统奇异值分布的柱形图如图7所示，系统阶次取n2;得到系统的系数矩阵后，将预测输出与实际输出的差值作为目标函数，判断其是否小于等于容许误差，即≤ε;若满足上述条件，则辨识结束，输出模型参数{α，q，M，A，B，C，D};否则令迭代次数ii+1，重复频域分数阶子空间辨识步骤，直到结束条件满足为止.

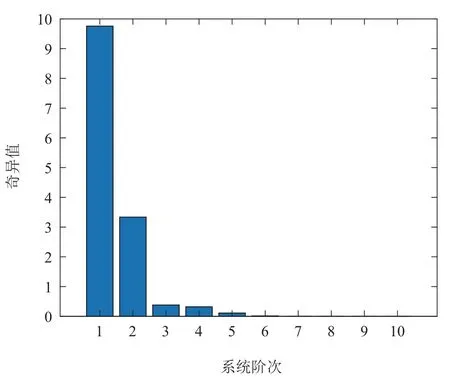
图7 PEMFC系统奇异值分布图Fig.7 Singular value distribution of PEMFC system

4.4 GA-PSO优化过程

对GA-PSO混合优化算法中的粒子种群和参数初始化，其中种群规模N20，惯性权重的上下限值ωmax0.9，ωmin0.4，最大迭代次数Gmax100，交叉概率pc0.5，变异概率pm0.05，粒子速度的上下限值Vmax1，Vmin-1，粒子位置的上下限值Xmax10，Xmin-10，学习因子c1和c2的初始值c1s1，c2s1.5，终止值c1e2.5，c2e2.75.另外，适应度函数为模型实际输出与预测输出的均方根误差(root mean square error，RMSE)，遗传算法的选择操作采用轮盘赌法，学习因子的取值方法采用非对称线性变化取值法，并选用线性惯性权重递减策略.

5 仿真结果

为了验证频域分数阶子空间辨识算法及改进优化算法的有效性，用输入/输出数据进行辨识和验证.以式(22)为目标函数，待优化参数为同元分数阶次α(0＜α ＜2)、辅助阶次q(2＜q ＜10)以及频域采样点数M(2＜M ＜20).经过GA-PSO的寻优和频域分数阶子空间辨识过程，得到优化参数和PEMFC电特性FOSS模型的值如下:

基于GA 优化[17]、PSO 优化[18]、GA-PSO 优化的PEMFC频域分数阶子空间辨识模型的辨识结果如图8-11所示.

从图8-9中可以看出，带GA优化、带PSO优化与带GA-PSO优化的频域分数阶子空间辨识方法辨识得到的输出均能够跟随实测数据的变化趋势，但都存在一定的误差.通过图10-11可以看出，带GA-PSO优化的频域分数阶子空间辨识的输出电压误差绝对值小于0.25 V，输出功率误差绝对值小于0.63 W.与带GA优化、带PSO优化的频域分数阶子空间辨识相比，误差较小，精度更高.带GA-PSO优化的频域分数阶子空间辨识能够更精确的描述PEMFC的电特性.表1为频域分数阶子空间辨识与时域分数阶子空间辨识[12]的辨识时间比较.

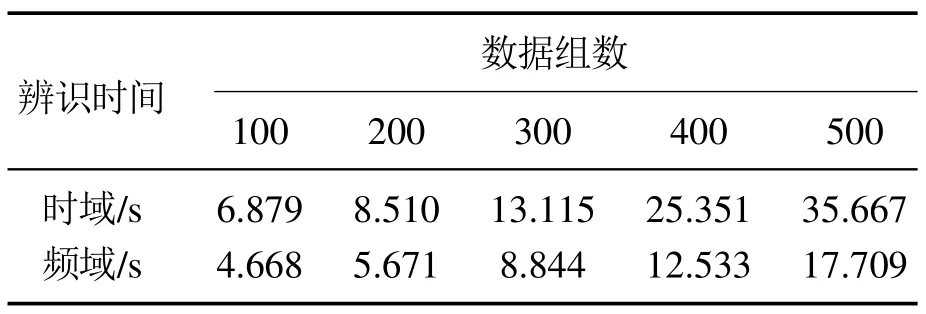
表1 频域与时域分数阶子空间辨识的辨识时间比较Table 1 Time comparison of fractional subspace identification in time domain and frequency domain

图8 输出电压Fig.8 Output voltage

图9 输出功率Fig.9 Output power

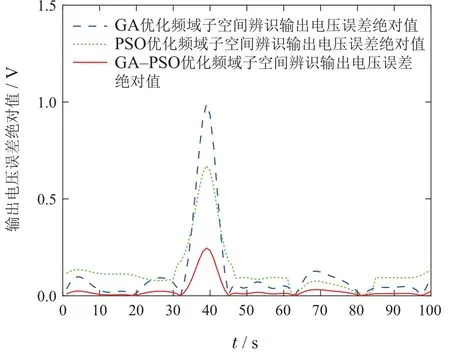
图10 输出电压误差绝对值Fig.10 Absolute value of output voltage error

图11 输出功率误差绝对值Fig.11 Absolute value of output power error

从表1可以看出频域分数阶子空间辨识的辨识时间明显比时域分数阶子空间辨识短.当辨识数据组数取100，200，300时，频域分数阶子空间辨识的辨识时间大约是时域分数阶子空间辨识三分之二;当辨识数据组数取400，500时，频域分数阶子空间辨识的辨识时间大约是时域分数阶子空间辨识二分之一.由此可以看出，频域分数阶子空间辨识能够大大减小计算复杂度.

6 结论

本文针对PEMFC发电过程中存在的分数阶特性，建立了PEMFC电特性的FOSS模型.在频域子空间辨识方法中引入分数阶微积分理论，提出一种频域分数阶子空间辨识方法.对影响PEMFC系统电特性的因素进行分析，选取负载电流、氢气流量为模型输入，输出电压和功率为模型输出，采用上述频域分数阶子空间辨识方法得到系统的系数矩阵，并在辨识过程中采用一种GA-PSO混合优化算法对辨识算法中的未知参数进行寻优.仿真结果验证了算法的有效性，频域分数阶子空间辨识得到的模型能够准确地描述PEMFC的电特性变化过程.