居住街区形态特征与PM2.5 相关性研究
——以北京市中心城区两个居住街区为例
2022-09-17张培浩北京工业大学城建学部建筑与城市规划学院硕士研究生
文/张培浩 北京工业大学城建学部建筑与城市规划学院 硕士研究生
引言
快速的城市化进程使得城市规模剧增,建筑密度加大且建筑高度增加,改变了城市下垫面的形态特征,同时也改变了城市局部地区的气候环境,并对大气污染物迁移扩散产生影响[1]。随着人们生活水平的提高,对于生活空间的环境品质也愈加重视。如何通过合理规划设计城市空间强化大气污染物的传输扩散、改善环境空气质量,成为相关学科关注与探索的焦点。在上述背景下,城市形态学从单一学科研究转向多学科的交叉研究,有关城市形态与空气质量的相关研究逐渐展开。
近年来,随着研究方法的丰富与新型软件的应用,城市形态与空气质量之间的关系被确立起来[2,3],目前有关研究主要关注在城市或区域较大尺度上,研究内容包括典型污染物的动态变化特征、时空演化、来源解析和成分分析等方面[4,5],研究表明,城市空间布局、用地结构对大气污染物的分布与传输有着密切的关系[6,7],进而影响城市区域的空气质量。戴菲等基于武汉市域内18 个常规大气监测点数据的基础上,综合考量了地表覆盖与垂直空间类城市形态参数与大气污染物浓度之间的关系[8]。城市街区是承载居民活动的基本规划单元,P.Edussuriya 等证实了街区尺度上空间形态参数与PM2.5和CO的相关性[9]。近年来,计算流体力学(Computational Fluid Dynamics,CFD)数值模拟技术的兴起为研究中小尺度上城市形态与大气环境质量的相关作用机制提供了技术支撑,并为将绿色健康理念融入城市空间规划设计提供了可行性,有学者利用CFD 模拟典型大气污染物在街区尺度上的空间分布与扩散规律[10,11]。
综上,在街区尺度上对建筑空间布局,特别是加入植被后的城市形态与污染物扩散之间的详细研究鲜有报道,较少有研究利用实地监测与国控站点的多元数据对CFD 模拟进行校核。此外,现有研究对于城市形态指标体系的构建缺乏系统的方法,缺少对非物质形态(包括人口、经济、社会等)指标的考虑。
本研究聚焦于特大城市中的街区尺度,基于对包括植被覆盖率与人口密度等非物质形态指标在内的城市形态参数筛选,通过对北京中心城区某居住街区气象数据和PM2.5 实地监测、包含植被要素的CFD 数值模拟和多源数据校核,研究城市形态对街区空气质量(以PM2.5 为例)的影响,为健康宜居的城市规划设计提供科学依据。
1 研究区域与研究方法
1.1 研究区域
居住类街区是承担人群日常生活最多的城市空间,也是构成城市肌理的基本单元。根据街巷网络、建筑组团布局形态等因素,选取北京市中心城区某中低层住宅街区A 和高层住宅街区B(图1)。其中,街区A 多为中低层围合住宅,属于典型老旧小区布局形式;街区B以板式高层住宅为主,建筑体量较大,分散式布局。上述两个居住街区具有不同的功能定位和空间形态特征,能够代表性地反映北京居住街区尺度上城市形态特征对大气污染物迁移扩散的影响。
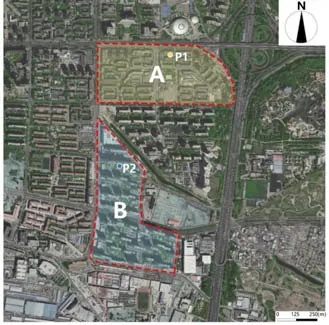
图1 研究区域示意图(图片来源:作者自绘)
1.2 PM2.5 监测与数据分析
PM2.5指大气中粒径d≤2.5μm的细粒子,可以通过呼吸进入人体,对人体健康产生危害,是反映环境空气质量的重要指标之一。
选用XL68 型智能环境监测设备,于2019 年夏秋两季共23 天,在监测点位P1、P2(图1)(高度分别为3m、3m)对街区内部风速(精度:0.1m/s,量程:0 ~60m/s)、风向(精度:0.1°,量程:0 ~360°)、PM2.5 浓度(精度:1μg/m3,量程:0 ~1000μg/m3),全天实地监测。监测结果见图2、图3。
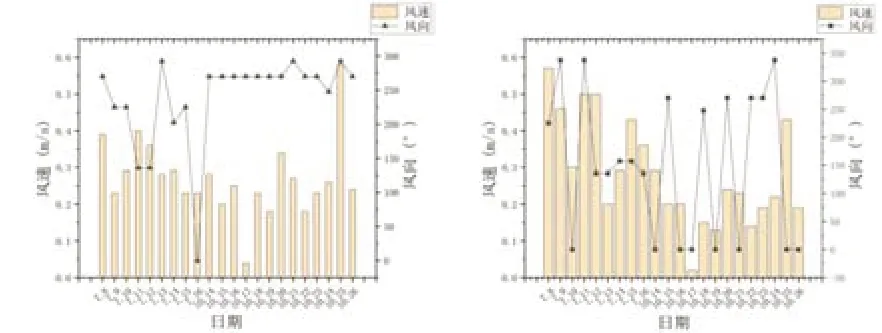
图3 P1(a)监测点与P2(b)监测点风速与风向统计图(0°为正北,90°为正东)(图片来源:作者自绘)
图2 为街区A、街区B 与临近的国控点(相距约7km)PM2.5 浓度数据对比,总体来看,街区内部污染物浓度变化趋势受城市整体背景浓度的影响,但街区A 与街区B 表现出了一定的局部差异性。

图2 PM2.5监测点浓度统计图(图片来源:作者自绘)
1.3CFD 模拟
相较于风洞试验、现场监测等环境空气质量研究方法,CFD 模拟有着快速便捷、数据全面等特点,可以从不同角度分析街区尺度风环境与大气污染物浓度之间的相关作用[12,13]。
1.3.1 控制方程及湍流模型
采用基于有限体积法的ANSYS Fluent 进行CFD 数值模拟[14],主控方程为三维定常雷诺平均Navier-Stokes 方程,湍流模型采用标准K-ε 湍流模型。该湍流模型已广泛应用于室外风环境与污染物浓度的模拟中,且模拟结果与实测数据取得了较好的一致性[15]。
控制方程为雷诺平均Navier-Stokes 方程:
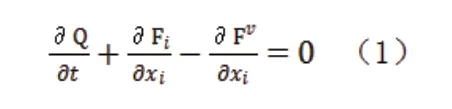
式中,Q——流动守恒变量
Fi——无粘通量
Fv——粘性通量
树木对周围流场有降低风速,增加扰流的作用,根据相关文献[16]对树木的处理方法,采用在动量方程、K 方程、ε 方程分别添加源项的方法来实现树木冠层对流场影响的模拟效果。
1.3.2 计算域与网格生成
将所选两个街区的建筑与树木(6m×6m×3m 长方体)进行比例建模,以街区边缘为中心,半径5H(H 为区域内最大建筑高度)建立水平计算域,垂直距离3H 建立垂直计算域(图4)。采用CFD-ICEM 进行网格划分,为节约计算成本,采用以六面体为主的非结构化的网格划分方法,并对建筑物与树木部分网格做局部加密处理,最终确定街区A 网格总数为2.8×108 个,街区B 网格总数为2.4×108 个。
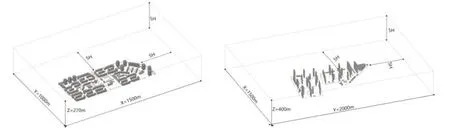
图4 计算域A(a)与计算域B(b)示意图(图片来源:作者自绘)
1.3.3 边界条件与求解设置
平均风速的分布随高度呈指数分布,速度入口边界条件采用对数函数曲线[17]。
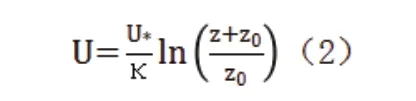
式中,U——高度z(m)处水平风速(m·s-1);U*—— 地 面 摩 擦 速 度(m·s-1);κ——Von·Karman 常数,κ=0.42;z0——地表粗糙度,z0=0.25。
出流边界条件采用零压出流边界条件(pressure oulet),建筑物和地面选用无滑移壁面边界条件(no slip),粗糙度(roughness height)分别取值0.0025m、0.003m,粗糙度常数(roughness constant)取值0.75;计算侧边界与上边界采用对称面(symmetry)边界条件[18]。
此外,由于树木对周围流场的作用,将树冠部分作为多孔介质处理[19]。同时树木对污染物具有吸附沉降的作用,其中沉降速率由风速和污染物浓度决定[20]。
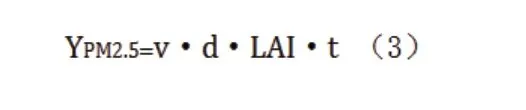
式中,YPM2.5——单位面积的乔木对污染物滞尘量(μg·m-2);v——污染物PM2.5 沉降到叶表面的速率(m·s-1);d——污染物浓度(μg·m-3);LAI——植被叶面积密度(m2·m-3);t——滞尘时间(s)。研究采用在标准K-ε 方程添加源项的方法,通过Simple算法,空间的差分格式为二阶迎风差分格式来模拟空气流动,以组分输运方程求解污染物浓度。
城市街区建设的密集程度反映了各类物质空间在地表上的密集程度,在密度类特征中选取建筑密度(Building density,BD)作为研究参数,建筑密度指建筑基底面积与街区用地面积的比值,反映了区域建筑的密集程度,计算公式如下:
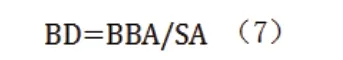
1.4 城市形态参数的选取
本研究基于已有研究的归纳梳理,将城市形态特征分为:规模类特征、功能类特征、密度类特征、结构类特征、形状类特征与非物质形态特征六类,并对不同城市形态特征与污染物水平之间的相关性进行分析。基于街区尺度上、对污染物水平的潜在影响、便于控规及设计阶段实施等原则,结合上述形态特征与环境空气质量的相互作用机制、以及相关文献研究进展,筛选出10项形态参数进行研究。
街区形态的差异首先体现在规模尺度的差异,在规模类特征选取总建筑面积(Total building area,TBA) 与 容 积 率(Floor area ratio,FAR)作为研究参数,总建筑面积指街区所有建筑物面积之和,反映了区域开发建设的规模;容积率(Floor area ratio,FAR)街区建筑面积与街区用地面积的比值,反映了区域的建设强度,计算公式如下:
式中,BBA——建筑占地面积;SA——总用地面积。
街区结构的差异反应在街区的建筑布局形式及开敞空间的结构分布,在结构类参数中选取街区 围 护 度(Average building envelope,ABE)与空间开放度(Space openness,SO)作为研究参数。
建筑平均围护度指街区建筑围护结构周长与街区用地周长的比值,反映了街区空间被建筑的围合的程度,计算公式如下:
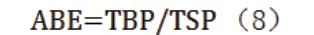
式 中,TBP—— 街 区 围 护 结 构 周 长;TSP——街区总周长。
空间开放度指街区未被开发空间面积与容积率的比值,反映了街区开敞空间的开放程度,计算公式如下:
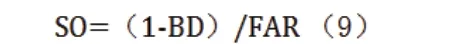

不同功能的用地属性对污染物的传输及扩散具有不同程度的影响[4],在功能类特征中选取植被覆盖率(Greenbelt coverage rate,GCR)作为研究参数,植被覆盖率指街区植被水平投影面积与街区用地面积的比值,计算公式如下:
式中,BD——建筑密度;FAR——容积率。
建筑单体形态的差异表现在建筑体量、建筑结构等方面,在形态类参数中研究选取建筑平均体积(Average building volume,ABV)、建筑平均层数(Average building floors,ABF)与建筑高度标准差(Standard deviation of building height,SDH)作为研究参数。
建筑平均体积指街区内建筑体积的平均值,反映了街区内部建筑的体量的一般水平,计算如下:
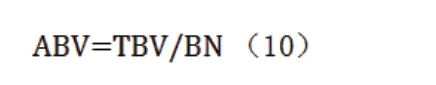
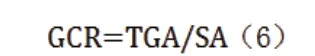
式中,TGA——植被覆盖面积;SA——街区用地面积。
式中,TBV——街区总建筑体积;BN——建筑数量。
建筑平均层数指街区内所有建筑的平均层数,反映了街区内部建筑高度的一般水平,计算如下:
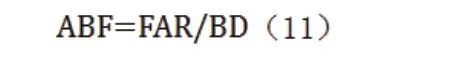
式中,FAR——容积率;BD——建筑密度。
建筑高度标准差指街区内所有建筑高度的标准差,反映了街区内建筑高度差异程度,计算公式如下:
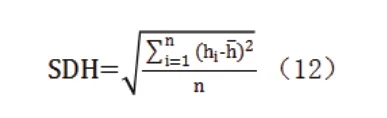
式中,hi——单体建筑高度;h——建筑平均高度;n——建筑数量。
物质空间形态特征是非物质空间形态特征在街区内部上的空间投影,在非物质空间形态特征中选取人口密度(Population density,PD)作为研究参数指街区人口规模与街区用地面积的比值,反映了街区内部的人口密集程度,计算公式如下:

式中,TP——街区总人口;SA——街区用地面积。
2 模拟结果与误差分析
2.1 不同街区数值模拟结果
以不同日期的北京气象站地面观测数据作为模拟的初始条件,选取监测期间具有典型气象特征 的7 月10 日、7 月13 日、10 月14 日、10月26 日建立CFD 数值模型,模拟预测街区A 与街区B 各典型日期的全时空PM2.5 浓度分布与风环境,模拟结果见图5。
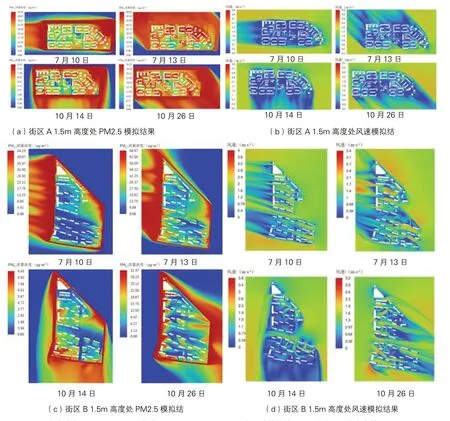
图5 1.5m 高度处街区A(a)、(b)与街区B(c)、(d)PM2.5 与风速模拟结果(图片来源:作者自绘)
从街区A 与街区B 模拟的整体结果来看,街区建筑物对上风向的污染物起到了不同程度的阻隔作用,道路是污染较严重的区域。其次,建筑背风侧容易产生较大面积的静风区域,形成污染物的堆积。对风速与PM2.5 的模拟结果进行对应分析,可发现风速越高的区域,污染物越容易扩散。
2.2 不同街区模拟结果差异性
模拟结果显示,街区A 与街区B 在1.5m 高度处的PM2.5 空间分布存在一定的差异性,街区B 整体PM2.5 扩散效果优于街区A,而街区A 局部区域表现出污染物堆积现象。在同一街区中,形态特征的局部差异也对污染物的扩散产生了一定的影响。因此,探讨相关形态参数与风环境和污染物分布之间的关联性,可为通过空间优化设计改善空气质量提供参考。
2.3 误差分析
使 用IBM SPSS Statistics 24.0 对P1、P2 点的模拟数据与实测数据的平均值进行相关性检验。同时应用配对t 检测,检验监测数据与实测数据之间是否存在显著性差异,结果见表1。在相关性检验中,风速、PM2.5 数据表现出了较高的相关性(R2=0.82,0.77),模拟结果与实测数据具有较好的一致性;在配对t 检验中,模拟风速和PM2.5 浓度与实测数据之间不存在显著性差异。因此,建立的CFD 数值模型能够较为准确地预测街区风场与PM2.5 浓度。

表1 P1、P2 模拟数据与实测数据配对样本检验(表格来源:作者自绘)
3 街区形态特征与PM2.5 的相关性分析
基于各形态参数与风速、PM2.5 的相互作用,将1.5m 高度处(行人高度)的相对风速、PM2.5 相对浓度作为因变量,以所选形态参数作为自变量,通过皮尔森(Pearson)双变量相关分析所选形态参数与PM2.5、风速的相关性。
3.1 街区形态特征要素提取
同一街区具有不同形态特征的街区单元,街区单元划分较小会影响分析的真实性,街区单元划分较大会导致样本点较少。根据典型城市街区尺寸,将街区A 与街区B 划分为200m×200m 的街区单元(图6),共二十个样本单元,在每个街区单元内进行形态参数及污染物浓度的相关计算。

图6 街区网格划分示意图(图片来源:作者自绘)
3.2 相关性分析
根据相关性分析结果(表2),不同街区形态参数对街区内部风速与街区内部污染物浓度的影响不一致,在十个计算变量中,BD、ABE、ABV、ABF、SDH、GCR 对PM2.5 浓度及风速表现出较强的相关性,相关系数在0.4 ~0.8 之间;TBA、FAR、SO、PD 与PM2.5 浓度及风速之间相关性较弱,相关系数低于0.3。相关性较高的形态参数通过对风环境的影响进而影响污染物的传输与扩散,其中BD、ABE 与风速呈现显著的负相关关系,与PM2.5 呈现出一定的正相关性;ABV、ABF、SDH 与风速呈现显著正相关,与PM2.5 呈现出一定负相关性;GCR 与风速、PM2.5 均呈现出明显的负相关关系。
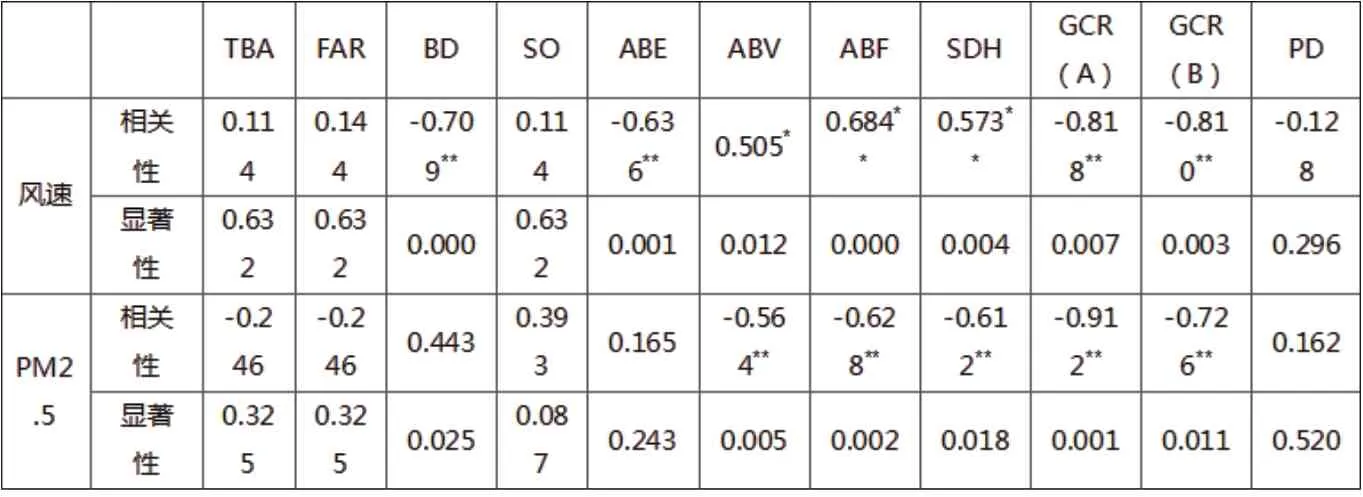
表2 不同街区形态参数与风速、PM2.5 相关性分析(表格来源:作者自绘)
根据相关性系数,随着BD 与ABE 的升高,风速逐渐降低,PM2.5 浓度逐渐上升。以街区A与街区B 局部区域10 月14 日模拟结果为例(图7),相较于街区B,较高的BD 与ABE 降低了街区A 内部的风速,导致街区内外的空气流通受阻,进而影响了污染物的扩散。
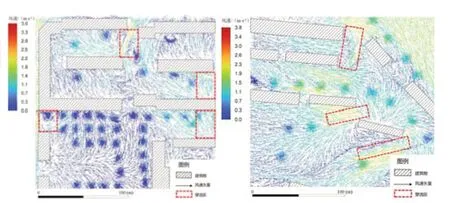
图7 街区A(a)与街区B(b)局部区域风速矢量图(图片来源:作者自绘)
以ABV、ABF 为代表的形态类参数一定程度上反映了建筑的体量,随着ABV 与ABF 的升高,建筑体量增大,间接地增加了街区内部的公共空间占有率,进而增加了街区内同外部空间洁净空气交互的可能性,实现了污染物的快速扩散;SDH 体现了街区内不同建筑之间的高度差,当街区内部建筑高度差达到一定程度时,会在建筑水平方向与垂直空间内形成局部穿流区(来流风与建筑边界交接的区域),局部区域风速增大,加强了污染物向背风侧的扩散。
以GCR 代表的功能类参数主要表现出对风速的削减及PM2.5 的滞尘,植被通过降低冠层以下的风速,将污染物滞留于植物叶片表面(图8),进而降低了区域周围的PM2.5 浓度水平。
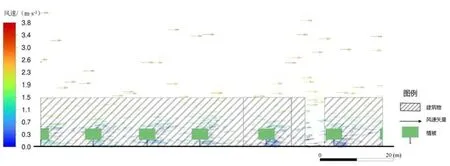
图8 街区A 局部区域XZ 平面风速矢量图(图片来源:作者自绘)
3.3 基于污染物扩散的街区形态优化策略
综上,街区内部形态参数主要通过影响风速间接影响PM2.5 的扩散,即作为街区形态与污染物扩散的中间机制,风环境仍然是影响污染物扩散的主要因素。依据上述分析,研究提出基于污染物扩散的居住街区形态优化策略:(1)通过适当降低建筑密度与平均围合度,以增强街区内外空气流通,促进街区内部污染物扩散;(2)适当增加建筑单体体量,以增加街区内部开敞空间的面积,同时合理控制街区的建筑高度差,形成高低错落的建筑布局形式,降低对来流风的阻碍作用,增强局部地区污染物扩散能力,形成良好的通风廊道;(3)增加街区植被覆盖率,降低局部地区风速,在植被类型选取方面,考虑适宜高度的植被种类,增强PM2.5 的吸附沉降。
结语
基于北京市典型居住街区形态特征及其风场、PM2.5 实地监测,采用CFD 数值模拟方法建立了居住街区风环境和PM2.5 分布预测模型,经模型验证与校核,预测结果与实测数据之间不存在显著性差异,具有较好的一致性,能够用于不同模拟条件下街区风场与PM2.5 浓度预测,为分析街区城市形态与环境空气质量的相关性提供了研究手段。
依据研究街区形态特征及所建立的街区CFD 模型,分析了对空气质量有潜在影响的10项形态参数与风速、PM2.5 的相关性,其中,BD、ABE 等形态参数对街区内部风速与PM2.5浓度表现出了较高的相关性,而TBA、FAR、SO、PD 表现出较差的相关性。
总体来看,在相同用地性质的前提下,不同形态参数主要通过影响风环境间接影响污染物扩散。因此,在未来居住街区规划时,应从防止污染物扩散的角度,将城市规划设计与空气质量管控相结合,以便调控城市空间对城市环境的不利影响。提出如下城市规划设计建议:(1)适当降低街区建筑密度与围护度;(2)适当增加街区内平均建筑体积与平均建筑层数,合理区分不同的建筑高度;(3)增加街区的绿化覆盖率,考虑适宜高度的植被种类。
