一种陶瓷砖破坏强度和断裂模数测量不确定度的评定*
2022-09-17朱礼兵兰书元胡江峰
朱礼兵 龚 明 兰书元 胡江峰 张 鹏
(江西省建筑卫生陶瓷质量监督检验中心 江西 高安 300800)
随着高新技术地迅速发展,对各行业实验室检测、校准结果的可靠性要求越来越高,除了要获得检测或校准结果外,还要求知道检测或校准结果的测量不确定度。国际实验室认可合作组织(简称ILAC)、亚太实验室认可合作组织(简称APLAC)、中国合格评定国家认可委员会(简称CNAS)都对实验室体系运行中检测结果的测量不确定度评定和应用提出了新的要求。大量试验研究表明,为了提高测量不确定度评定的可靠性,对材料不同的检测参数和检测方法应该采用不同的评定方法。对于材料理化检测结果测量不确定度的评定,采用直接评定法无法评定具有一定难度的检测项目,而采用综合评定法能较好地解决材料理化检测结果测量不确定度评定中的许多难点,不仅使检测结果不确定度的评定具有可行性,而且能提高检测结果测量不确定度评定的准确度和可靠性。
笔者结合陶瓷检验检测实验室多年的工作经验,根据国家标准GB/T 3810.4-2006陶瓷砖试验方法第4部分 断裂模数和破坏强度的测定,以适当的速率向陶瓷砖表面施加正压力,通过读取破坏载荷值,测量砖的宽度、厚度,来测定陶瓷砖的破坏强度和断裂模数。同时结合实际测量过程中各个因素对其影响程度,对陶瓷砖破坏强度和断裂模数的不确定度进行了评定。
1 测量过程
测量对象:高级镜面水晶砖(罗夫伦商标),国家标准GB/T 4100-2015陶瓷砖附录K 干压陶瓷砖,吸水率6%<E≤10%BⅡb类。
测量依据:国家标准GB/T 4100-2015陶瓷砖。
测量环境:温度一般为(20±2)℃,本实验工作环境温度为20℃。
测量仪器:数显陶瓷砖抗折试验机(TZS型10000档抗折机(J-15)),宁夏机械研究院;
数显游标卡尺:精度为0.02 mm,成都成量工具集团有限公司;
101电热鼓风干燥箱:温度为(110±5)℃,康恒仪器有限公司。
测量过程:根据标准,采用尺寸偏差、表面质量合格的高级镜面水晶砖中随机抽取7块试样,并用硬刷刷去试样背面松散的粘结颗粒。
将试样放入温度为105℃的干燥箱中,烘干至恒重;然后放入干燥器冷却至室温,3 h后将试样放在抗折机上进行实验,用数显游标卡尺测出试样的宽度以及实验后沿断裂边测得试样断裂面的最小厚度。根据试样长度调节两根支撑棒之间的跨距为480 mm,并以1 N/(mm2·s)的速率均匀地向砖的表面正中心施加压力直至破坏,记录此时的最大破坏荷载F,根据公式S=FL/b算出砖的破坏强度,最后用破坏强度除以沿破坏断裂面的最小厚度的平方,即得到断裂模数[1]。
2 建立数学模型
2.1 破坏强度计算式

式中:S-破坏强度,N;
F——破坏荷载,N;
L——跨距,mm;
b——试样宽度,mm。
2.2 断裂模数计算式
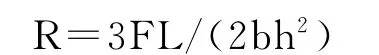
式中:R——断裂模数,MPa;
h——断裂面最小厚度,mm;
其它符号含义同破坏强度计算式。
2.3 合成不确定度计算式[2]

Urel(L)——两根支撑棒之间的跨距L 所引起的不确定度(因为由于跨距值为常数,故此项不确定度分量可视为零);
Urel(b)——试样宽度b 的测量所引起来的不确定度;
Urel(h)——试样破坏断裂面最小厚度h 的测量所引起的不确定度;
Urel(rep)S——重复性实验所引起的破坏强度不确定度;
Urel(rep)R——重复性实验所引起的断裂模数不确定度。
由于Urel(L)不确定度分量为零,故上述合成不确定度可简化为:

3 检验原始数据
(1)检验方法:根据国家标准GB/T 3810.4-2016陶瓷砖试验方法 第4部分:断裂模数和破坏强度的测定;
(2)样品规格:500 mm ×500 mm;
(3)跨距:按标准要求,跨距为480 mm;
(4)具体的实验数据见表1。

表1 实验数据表
4 输入量的标准不确定度分量
4.1 重复性引起的不确定度分量Urel(rep)S、Urel(rep)R
根据贝塞尔公式计算可知:

4.2 最大破坏荷载F引起的不确定度分量Urel(F)
最大破坏荷载F 引起的不确定度主要包括仪器的测量不确定度和仪器校准的不确定度两个方面。
4.2.1 仪器的测量不确定度U1rel(F)
查仪器说明书(合格证书),其示值误差要求值为±1%,且未标明置信概率,故按均匀分布估计不确定度分量,取k=3,因此仪器的测量不确定度:

4.3 试样宽度b引起的不确定度分量U rel(b)
由于测量试样宽度所用的数显游标卡尺精度是0.02 mm,可按照均匀分布估计不确定度分量,取k=3,试样宽度b测定的平均值b=500.13 mm,因此试样宽度b引起的标准不确定度:

4.4 试样破坏断裂面最小厚度h引起的不确定度分量U rel(h)
由于测量试样厚度所用的数显游标卡尺精度是0.02 mm,可按照均匀分布估计不确定度分量,取k=3,试样破坏断裂面最小厚度h 测定的平均值h=6.25 mm,因此试样破坏断裂面的最小厚度h所引起的标准不确定度:

试样破坏断裂面的最小厚度h所引起的相对不确定度:
Urel(b)=U(b)/b=0.012/6.25=0.19%
4.5 不确定度分量核算
由表2可知,最大破坏载荷、断裂面最小厚度和重复性试验所引起的不确定度分量在总的合成不确定度中所占比例较大,需控制其影响因素,因此选购高精度、稳定性好的设备和实验人员严谨细致的操作至关重要。
5 合成相对不确定度和标准不确定度
(1)破坏强度S合成相对不确定度:


6 扩展不确定度
根据国家计量校准规范JJF1059.1-2012测量不确定度评定与表示,取包含因子k=2(置信概率为95%)可知,U=k×UC
(1)破坏强度S扩展不确定度:U(S)=k×UC(S)=2×4.08=8.16 N
(2)断裂模数R 扩展不确定度:U(R)=k×UC(R)=2×0.18=0.36 MPa
7 本中心测量不确定度报告
(1)破坏强度S=(637.27±8.16)N,其中扩展不确定度U(S)=8.16N(k=2),对于正态分布来说有95%的置信概率,完全满足标准和性能要求。
(2)断裂模数R= (24.50±0.36)MPa,其中扩展不确定度U(R)=0.36 MPa(k=2),对于正态分布来说有95%的置信概率,完全满足标准和性能要求。
8 结语
通过对陶瓷砖破坏强度和断裂模数测量不确定度各分量的分析核算可知,最大破坏载荷、断裂面最小厚度和重复性试验影响较大,因此选购高精度、稳定性好的设备和实验人员严谨细致的操作至关重要。
