基于最优化约束和模拟退火算法的钢板切割问题研究

2022-09-17李永圣马景涛甘惠材白博雄

科技与创新 2022年18期

李永圣，马景涛，甘惠材，白博雄

（哈尔滨理工大学，黑龙江哈尔滨 150081）

在钢材厂切割钢板时，先将原材料钢卷放在开卷机上，被送至剪切平台上进行剪切。剪切台上依次有剪切头和圆盘剪[1]。剪切头只能一刀切，如需额外横向切割，只能将材料移至小机器进行切割。生产板料时在切割后直接下料，卷料则需通过卷取机压臂成卷后再入库。原料在切割成品时若有剩余，符合余料标准的回收入库下次使用。对于钢材厂而言，如何提升成材率就是需要考虑的关键因素。本质等同于在固定的立体空间中尽量塞入多的大小不一的箱子，即把某种离散对象按照某种已经确定的约束条件进行安排，当得知符合这种约束条件的特定安排存在时，求解此种特定安排在某个优化准则下的最大解或最小解的离散组合最优化问题。

1 基本模型构建与分析

1.1 整数规划模型构建

将整数规划模型分为几个阶段，根据约束条件分别引入变量。

第一阶段考虑规划问题：

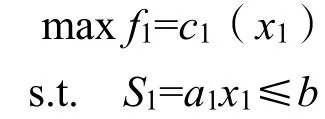
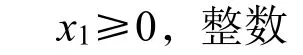
第二阶段考虑规划问题：

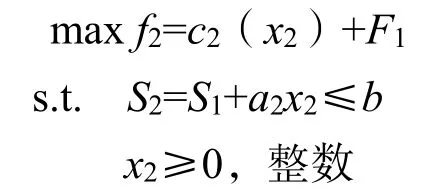
1.2 建立过程

程序变量为不同大小的产品，矩阵中存储着产品的长度y、宽度x，需要加工的产品只有卷材，共5 种，分别是订单1、订单2、订单3、订单4、订单5，这5个订单的Z分别为36、29、42、32、18。在数据库中任意选择一个产品，之后继续任意选择一个产品编号为j，使j产品紧紧挨着产品i放置。由于卷料都特别长，为了避免成材率过低，也减轻程序运算的负担，规定主程序选择的原材料长度都大大长于1—5 号产品，也就是只选择长度在10 万以上的原材料，即只有1、6、8 和9 这4 种原材料被程序选择。将产品逐个编号，范围为1—157。

程序从矩阵中随机抽出一个产品，放置在矩阵右上角。假设该产品编号为i。程序在数据库中任意选择一个产品，将其安放在原材料左上角，之后继续任意选择一个产品编号为j，使j产品紧紧挨着产品i放置，此时原材料被用去的宽度为xi+xj，当小于xi时，就继续添加产品直至产品的总宽度大于等于xi。为了避免重复添加，已经被添加的产品会在存储矩阵中被删除。排列方式如图1所示。

图1 排列方式

假设某一行排列了b个产品（由于排刀上限，b＜6），无法再增加新的产品了，那么在切割完本行产品之后需要重新排刀与进行一刀切，即切头剪。切头剪的位置选取的是这b个产品当中最长的那个，即最大的那个，假设为yp。此时，切刀的位置就是y－yp。之后在新的一行重复产品的选择流程，直到矩阵中存储的产品都选择到。

在剪切过程中原材料因为被剪切而不断变短。如果剩余原材料短于整个存储矩阵中最短的产品，即没有合适的产品能与之匹配，则更换材料。程序在运行过程中必须随时保存中间结果，即统计产品面积，以及选择出符合题目要求的余料，然后根据面积比值计算成材率，作为优化的参考指标。

经过程序运算得到27个排列方案。

2 模拟退火算法的模型优化与改进

2.1 模型优化过程

模拟退火算法来源于金属材料退火过程的模拟，将金属加热到较高温度的过程中，金属内部粒子随温度升高从有序变为无序状，同时粒子内能升高，再让其缓慢冷却，此时粒子逐渐从无序趋于有序，每个温度都达到平衡态，最后在常温时达到基态，此时内能为最小[2]。首先从27个排列方式中随机选择一种排列方式作为最优排列[3-4]，用最优排列对原材料进行普通Kriging 插值预测，计算初始解的均方根误差。计算公式如下所示：

式（1）中：A为均方根误差；n为可行排列方案数；Si为原材料面积；Ci为产品的面积。

而后对最优排列作随机的变动从而得到一组新的排列，即是在余集中随机选择一个材料尺寸替换初始排列中的一个材料尺寸从而产生新的一种排列方案，对新排列方案继续进行普通Kriging 插值预测，计算A1与Δ=A1－A0。如果Δ小于等于0，则接受新排列为此时的最优解排列方案；但如果Δ大于0，则按照Metropolis 准则以概率P来选择新的排列方案，否则保留原排列方案。1—9 排列方案如图2所示。

图2 1—9 排列方案

Metropolis 准则：设从当前排列方案生成新的排列方案，如果新排列方案的排刀数小于原排列方案的排刀数（即A1＜A0），则将新的排列方案作为当前方案；否则，以概率P来选择新的排列方案。概率P的计算公式为：

此方案的最终成材率为71.03%。

2.2 识别算法的提出

卷料与板料长度相差过大，不宜混合生产。因此本文抽取了程序运算的部分中间结果，也就统计出了产品面积并选择出了符合题目要求的余料，然后根据面积比值计算成材率，发现启发式算法前期的搜索模式太过粗陋，因此根据数据演化的定量规律做了调整[5-6]。

尽量减少人工排刀数可以通过尽量扩大n来解决，减小再切割数则要求同一行的产品尽量是同一订单号的产品。尽量减少再切割数需要优先把相同的元素并排放置。

3 改进模拟退火算法

3.1 模型构建

改进以后的模拟退火算法使用随机的选择概率P，用来选择比目前差一些的排列方案，依靠一定的概率跳出局部最优排列方案这一陷阱，从而得到全局最优排列方案。设之前某个排列方案为x（n），算法通过排刀数这一指标，排列方案变为x（n+1），对应地，方案的排刀数由E（n）变为E（n+1），定义由x（n）变为x（n+1）的选择概率P为：

通过上述公式可以说明，当排刀数减小时，排列方案的变化会被选择（此时的概率P为1），当排刀数增加时，意味着此排列方案的变化偏离了全局最优排列方案，但是算法在此时不会放弃该排列方案的变化，而是对此变化进行一定的概率选择：在区间[0，1]中随机选择一个数，当随机选择的数小于P时，说明这种排列方案的变化是被算法接受的，否则拒绝排列方案的变化，进入下一步循环流程。选择概率P的取值不是固定不变的，而是动态变化的，它的大小是由排刀数的变化量决定。

改进后的模拟退火算法流程：①假设B是初始解，设定Bi=B，设定开始退火温度为T，令i=0；②设T=Ti，用参数T及Bi引入Metorpolis 抽样算法中计算，返回状态Ai作为本算法的当前解；③空冷阶段中，令T=Ti+1，式中Ti+1

选择合适的排刀数对本算法影响较大，排刀数越低，搜索性则越强，得到最优解的概率就越大，但程序运算时间会变得很长。本算法选取排刀数经过反复试验获得。本算法中循环链的链长表示为任何一个排列方案，或者为遍历次数，称循环数。如果想尽可能减少人工切刀的数量，解决方法就是优先把相同尺寸的材料并排放置。但这本质上和降低排刀数是部分矛盾的，优先排布相同尺寸材料降低了横向组合产品的自由度，导致降低排刀数的目标受到了阻碍。

因此，需要改进启发式算法，应优先保证排刀数降低，在此基础上尽可能降低人工切刀的数量。

最终切割方案板料的总排刀次数为128 次，再次切割的次数为307 次，卷料的总排刀次数51 次，再切割次数为64 次，板材的成材率为68.34%，卷材的成材率为71.03%。

3.2 算法优化

为了降低运算量，不能每添加一个产品就进行一次浮动放缩，应采取填缝的措施。添加完一行的产品后，以最长的产品为基准，与剩下的短的产品做比较，延长短的产品使其在允许的尺寸浮动范围内到达到最长产品的长度，如果短产品不能达到最长产品的长度，即把短产品延长到最大允许的浮动尺寸。采用这种思路，分别计算了板料和卷料的结果。材料尺寸变化图如图3所示。