一种水下爆炸冲击波压力调控方法*
2022-09-17徐维铮
黄 超,张 磐,曾 繁,徐维铮,王 杰,刘 娜
(1. 中国工程物理研究院高性能数值模拟软件中心,北京 100088;2. 北京应用物理与计算数学研究所,北京 100088;3. 中国工程物理研究院流体物理研究所,四川 绵阳 621999)
舰船抗水下爆炸冲击研究和设计非常重要。水下爆炸会使船体损伤和结构变形,并造成船载设备的损坏(如电子设备短路、断路或断裂、主轴的变形等)。在某些情况下,即使整船仍能保持良好的水密性,但也会因为设备的功能损伤而丧失战斗力。研究设备对水下爆炸冲击的抵抗能力,最有效的研究手段是冲击试验,包括实船爆炸试验、冲击机试验以及浮动平台试验。其中,实船爆炸试验是在战斗环境下验证舰船结构及其系统抗冲击能力的最佳途径,但费用高、对环境影响大、存在安全性风险;冲击机试验是利用撞击模拟设备冲击环境,一般适用于小型设备,且载荷形式较单一;浮动冲击平台是模拟舰船爆炸试验,通常在水池或水库中开展,设备的安装形式可与舰上保持一致,设备适用范围广,但是受水池承受TNT 当量限制(通常TNT 当量为几千克到几十千克),冲击强度较低,较难达到真实的战时冲击环境。
战争环境下的水下爆炸TNT 当量可达吨级,按照水下爆炸实验相似准则,在一次冲击波相似律条件下(相同的/,其中为装药量,为到装药中心的距离),模型实验采用小当量爆炸虽然能够保证入射冲击波的峰值压力与战争环境下的保持一致,但冲击波持续时间却小了约一个量级(图1(a))。而如果按照冲击因子(/)等效,则模型实验冲击波持续时间增加有限,峰值压力也变为战争环境下峰值压力的数倍(图1(b))。更重要的是,要求实验中受冲击的设备完全按照几何缩比也基本不太可能。因此,从实用和高效角度出发,发展能够与真实战争环境水下爆炸冲击波载荷等效的实验方法非常必要。
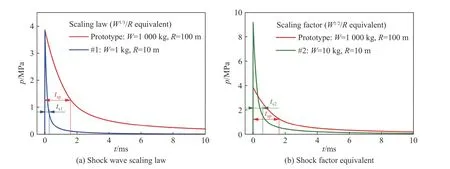
图1 不同相似准则下冲击波压力对比Fig. 1 Comparison of shock wave pressure curves under different similarity criteria
冲击波是爆炸能量输出的主要形式,影响冲击波传播的因素可分为外因和内因,外因是炸药所处的环境,如爆深、介质界面等,内因则是装药本身的性质,如爆轰性能、约束条件、起爆位置和装药形状。在使用环境和炸药类型确定的情况下,最主要的影响因素就是起爆位置和装药形状,这方面已有一些研究。Cole通过实验得到,对于一端起爆的长径比约15 的线形药包,在距离6.1 m 处观测到药包周围的压力-时间曲线存在差异,这种差异性在30.5~150 m 处依然显著。Hammond发现圆柱装药的近场冲击波压力特征与球形装药的有明显区别,主要体现在冲击波压力的幅值和持续时间方面。Sternberg计算验证了圆柱形装药水下爆炸存在非均匀的能量输出结构。赵继波等采用扫描相机测得了柱形装药水中爆炸轴向的近场冲击波压力衰减规律。李金河等通过冲击波压力测量,发现起爆方式对炸药水中爆炸初始及近场冲击波峰值压力的衰减有重要影响。王长利等对聚能装药水下爆炸近区压力分布进行了实验研究,发现水中近场冲击波具有较强的不均匀性,射流对正向冲击波有增强作用。Zhang 等和黄超等采用有限元法与边界元法或光滑粒子流体动力学(smooth particle hydrodynamics,SPH)方法相结合的耦合策略,建立真实装药爆炸模型,研究了初始装药形状和起爆方式对水下爆炸过程的影响,揭示了装药形状对气泡运动的影响机制。Zhang 等采用SPH 方法研究了成形装药水下爆炸冲击波的传输特性,发现装药轴向与径向冲击波的峰值压力存在显著差异。Huang 等基于实验和数值模拟方法,研究了细长装药水下爆炸冲击波传播和气泡运动过程,得到了装药长径比对冲击波方向性和气泡运动的影响规律。徐维铮等建立了锥形长药柱水下爆炸冲击波压力的计算方法,得到了长脉宽冲击波的分布规律。上述研究表明,通过起爆位置和装药形状对水下爆炸冲击波进行调控是可行的。
本文中基于细长装药技术和优化设计,设计一种在小当量装药条件下形成与真实战斗环境等效的水下爆炸冲击波实验方法,然后基于经过实验验证的冲击波模拟软件,对设计的装药方案进行计算验证,并对长药柱的水下爆炸能量输出规律进行分析。
1 冲击波压力调控方法
小当量水下爆炸冲击波与战争环境大当量水下爆炸冲击波的差异,主要在于前者的压力持续时间较后者的短得多,而我们希望通过装药结构的设计,在小当量条件下实现与大当量等效的冲击波压力波形。对细长装药水下爆炸冲击波的研究结果可知,在起爆端一侧冲击波压力的持续时间显著增长,且持续时间的长短主要由装药长度决定。如图2 所示,当装药从一端起爆后,爆轰波沿着装药轴向传播的同时,其后方的高温高压产物迅速膨胀,在水中形成冲击波向四周传播。基于简单波理论,如果将装药离散成不同的分段结构,那么随着爆轰波的传播,不同分段的装药相继被引爆,会在水中形成复杂的冲击波传播特征线,后形成的冲击波将在先形成的冲击波后面传播,由于其波阵面前的水已经处于被压缩的状态,导致这部分冲击波的传播速度更高,对前面的冲击波形成追赶。Cole曾经注意到线形装药的水下爆炸实验中经常看到多峰或多波头的现象,其本质就是不同部位装药爆炸冲击波追赶形成的叠加效果。在这样的机制下,细长装药轴向的冲击波会由于叠加效应被加强,主要表现为冲击波波形的变化和持续时间的增加。
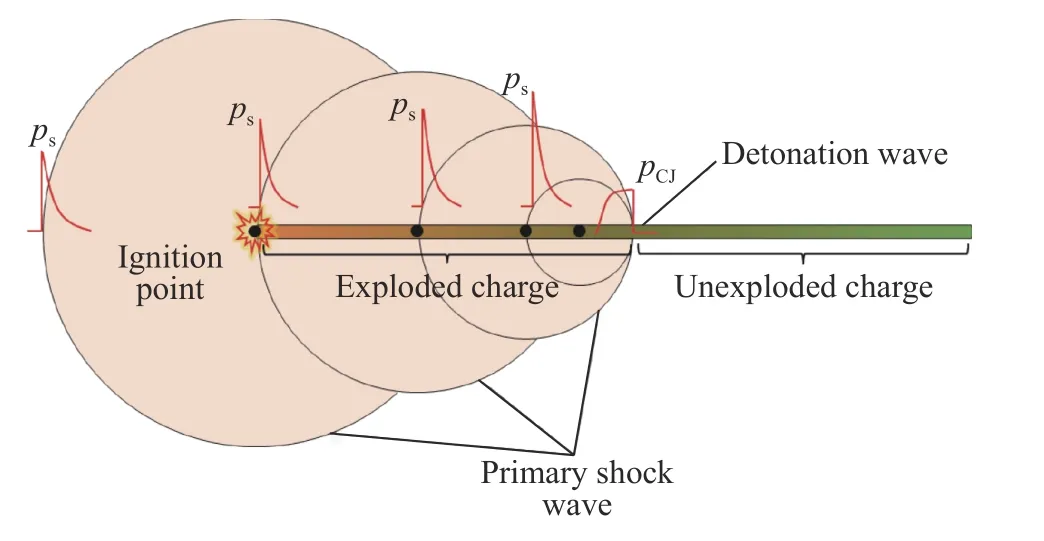
图2 细长装药水下爆炸冲击波的形成过程示意图Fig. 2 Formation of shock waves of slender charge underwater explosion
因此,可以通过调整装药长度,使冲击波的持续时间与战争环境大当量水下爆炸冲击波的持续时间趋于一致。此外,对于细长装药结构,从直径小的一端起爆,在起爆端一侧的冲击波峰值压力是显著降低的,如果改为从装药直径大的一端起爆,可以在不影响冲击波持续时间的基础上,提高起爆端一侧冲击波的压力。这样形成的装药设计方案如图3 所示,考虑加工生产的便利性,选用锥形细长装药结构,采用铸装TNT,在起爆端一侧形成与战争环境大当量水下爆炸等效的冲击波。在装药材料确定的情况下,冲击波压力由4 个参数共同确定:装药长度、直径和、测点距离。
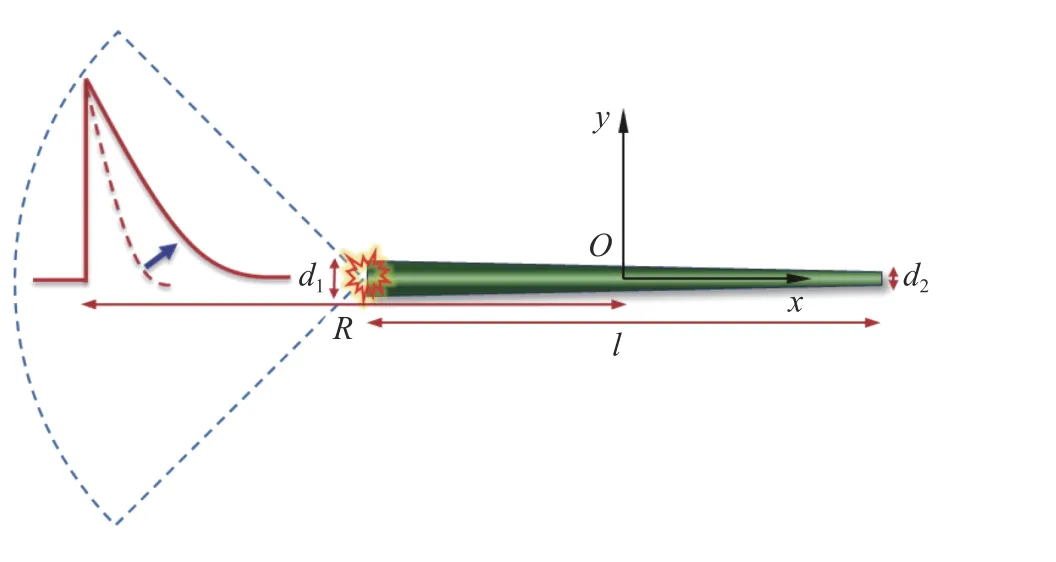
图3 装药设计方案Fig. 3 Design scheme of charge
上述4 个参数中,装药长度可根据冲击波持续时间等效的需求预先选取,其余3 个设计变量的确定可转化为参数优化问题,通过建立最优化设计的数学模型来计算。
首先,采用水下爆炸冲击波经验公式描述战争环境下大当量水下爆炸冲击波的压力-时间曲线,作为目标函数:
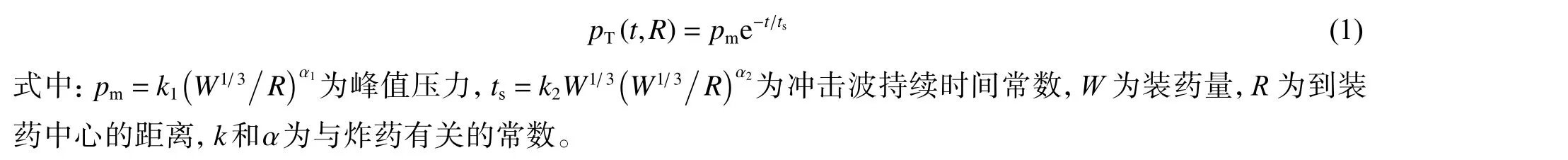
一般炸药爆轰的压力为10 GPa 量级,在水中形成的初始冲击波压力约为吉帕量级,对于这种强度不大的弱冲击波,其穿过介质时黎曼不变量基本保持不变,可采用简单波的连续过渡替代冲击波的不连续过渡。因此,可以采用声学近似(acoustic approximation)方法计算细长装药的水下爆炸冲击波压力:以装药中心为原点,把装药沿着轴向分为小段,每段炸药视为单独的装药,基于Wilkins 燃烧分数模型对细长装药采用时序爆轰模型进行控制,将第1~分段装药的冲击波压力进行叠加,同时对冲击波传播相互作用的非线性效应进行修正,进而计算流场中指定位置处的冲击波压力。这样,得到细长装药水下爆炸冲击波压力的设计变量函数为:
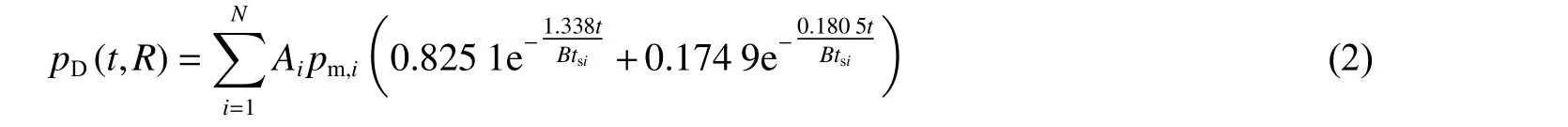
式中:、为第个分段装药的峰值压力和时间常数;A为峰值压力的修正系数,取A= 0.5/t,t为第段装药的冲击波到达测点经历的时间,这样每个修正系数是不同的,主要考虑了测点相对位置的影响,即不同分段装药的冲击波到达叠加点的过程存在差异,第段装药到达测点的冲击波会受到第1~-1 段装药到达测点的冲击波的影响;为时间常数的修正系数,对于文中的装药结构,取0.5。
从形式上看,目标函数式(1)中的自变量为时间和距离,式(2)的设计变量函数中除了时间和距离之外,还有装药的直径和、长度,可以将上述最优化问题转化为约束函数:
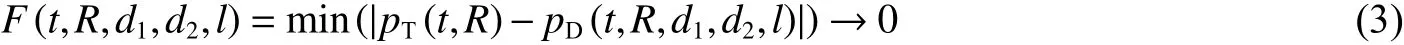
求解式(3)的目标是确定细长装药的几何参数(直径、长度)和冲击波压力测点的位置,从而得到与战争环境大当量水下爆炸冲击波最接近的压力-时间曲线。在采用式(3)进行参数设计时,首先应选取设计冲击波与原型冲击波需要等效的时间范围(如时间常数的1 倍或者更长),这样就可以确定装药的长度,因为细长装药冲击波压力的持续时间可由装药长度确定;然后按照装药爆轰的临界直径给定一个的初始值;最后选定一个合适的距离,采用牛顿法经过几次迭代试算,就能够快速确定参数,而不需要使用复杂的优化算法。
此外,为了减少变量的数量和取值范围,可以进一步加入以下条件约束:

式中:为装药的临界直径,装药直径必须不小于临界直径,才能使爆轰能够定常传播而不失效;为气泡最大半径;为安全系数,可根据经验确定。
与冲击波相比,气泡脉动压力的幅值通常要低1 个量级,气泡脉动主要对结构和设备造成低频冲击响应,而其持续时间则要比冲击波的持续时间高约1 个量级,气泡脉动更容易引起船体的低频振动。王志凯等研究发现,冲击波是影响浮动冲击平台冲击环境的主要因素,由于气泡载荷的低频特性,气泡脉动对浮动冲击平台的直接冲击作用只会小幅度增加浮动冲击平台冲击环境的谱速度值、谱位移值,对谱加速度值几乎无影响。当水下爆炸在结构附近形成气泡时,由于Bjerknes 力的作用可能形成指向结构物的射流。为了不影响实验效果,设置安全系数,以确保实验中气泡坍塌不会形成指向结构物的射流,可根据Blake 准则确定。结构物对气泡作用的强弱以零开尔文冲量线为分界线,在分界线上方Bjerknes 力较弱,不会形成指向结构物的射流:

2 数值模拟
采用数值模拟方法验证上述设计方法的有效性,并结合实验数据验证软件模拟的置信度。
2.1 数值模拟方法
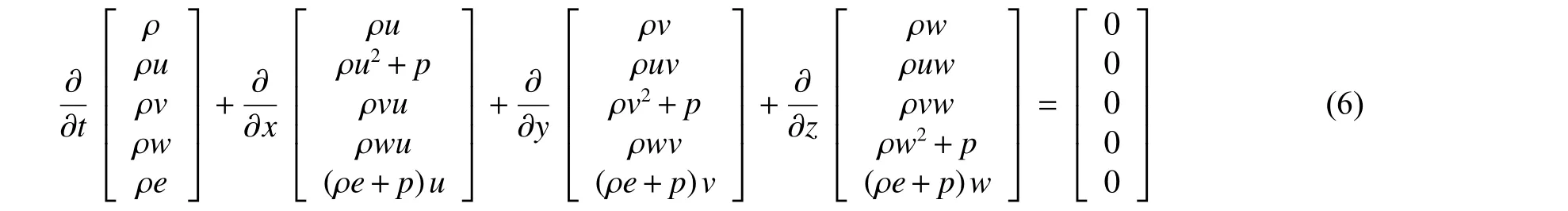
式中:ρ 为密度,、、为、、方向的速度,为压力,为比内能。
水介质的状态方程采用Tait 方程:

式中:γ、和为Tait 状态方程的拟合系数,对于水可取γ = 7.15、= 0.1 MPa、= 331 MPa,ρ为水的密度,下标“0”表示初始状态。
爆轰产物为气体时,使用JWL 状态方程计算产物中的压力:
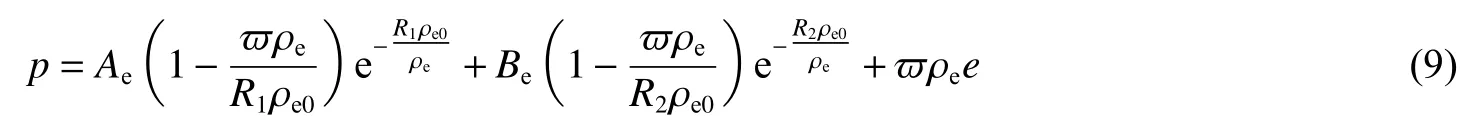
式中:ρ为炸药的密度,、、、和为JWL 状态方程中高、中、低3 段压力分别对应的拟合系数。对于TNT 可取:= 373.8 GPa、= 2.747 GPa、= 4.15、= 0.9、= 0.3、ρ= 1 630 kg/m。
在真实环境中,水中压力呈现非均匀分布,存在着压力梯度分布,假设水的密度不变,采用如下形式给出静水压分布:

式中:、和分别为大气压、重力加速度和水深。
按照N-S(Navier-Stokes)方程构件接口实现方程基本场的初始化,支持2 维和3 维问题模拟。边界条件和离散格式通过输入文件配置,采用有限体积离散格式,MUSCL2 阶重构算法求解,数值通量选取为HLLC。
1.写作兴趣不浓。教育心理学的角度来说,学习兴趣是一个人倾向于认识、研究获得某种知识的心理特征,是可以推动人们求知的一种内在力量。常言道:“兴趣是最好的老师,是入门的向导。”是推动学生写作的一种有效地内在动力,学生如果没有写作兴趣,写不出好的作文,所写之文不过是东平西凑,生拉硬拽。
2.2 置信度验证
通过实验考察软件模拟水中冲击波传输的置信度。实验在直径48 m、深23 m 的大型爆炸水池中开展。采用TNT 装药,锥形圆台结构,装药长2 m,左右两端的直径分别为35.9、71.8 mm,装药质量7.5 kg,密度1 580 kg/m。传爆药柱采用JH-14,TNT 当量24 g,传爆药中心预留雷管安装孔,通过电雷管从端部起爆装药,这样有助于分析起爆位置和装药形状逐渐变化对水下爆炸能量输出规律的影响。采用PCB-138A 压力传感器记录冲击波的压力信号,如图4(a)所示,以装药中心为原点,传感器P1~P5 分别布置在180°、135°、90°、45°和0°方位,距离装药中心4、6 或6.5 m 的位置,记录不同方向上、不同距离处的冲击波压力时间历程。
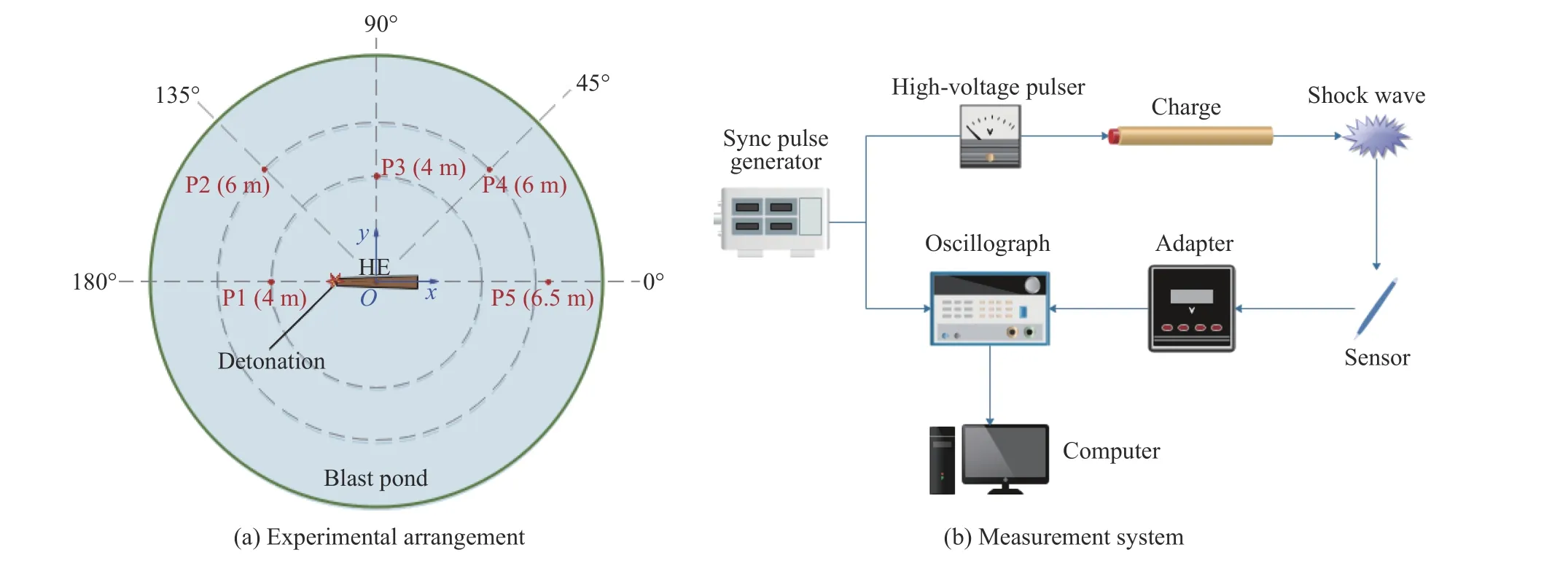
图4 实验布置及测试系统Fig. 4 Experimental arrangement and measurement system
测试系统由起爆台、同步机、示波器、适调仪、压力传感器和终端组成,如图4(b)所示。测试系统由同步机主控,其输出的同步信号同时触发起爆台、记录压力信号的示波器,实验后将示波器测量到的数据保存到终端。
在正式实验前,采用8 kg 标准TNT 药球进行水中爆炸预备实验,动态标定测试系统中压力传感器的灵敏度,预备实验结果表明,测试系统的测试精度控制在5%以内。此外还开展了一发重复性实验,在相同工况下,两发实验测得的冲击波压力曲线基本重合,最大偏差不超过3%,如图5 所示。
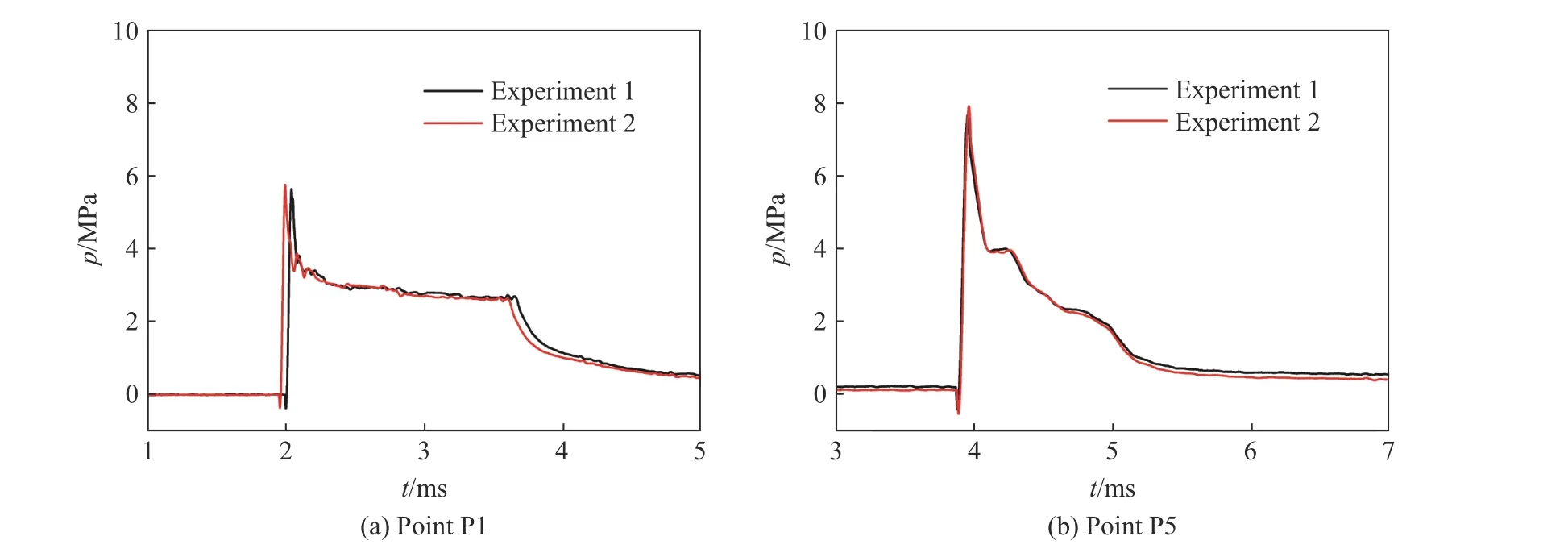
图5 冲击波压力-时间曲线的重复性实验结果对比Fig. 5 Comparison of repetitive experimental results of pressure-time curves
数值模拟的计算模型参照实验的布置建模,考虑到问题的对称性,采用轴对称模型,计算域选为∅8 m×16 m,经网格敏感性和收敛性测试,网格尺寸取10 mm 可兼顾计算的精度和效率。装药置于流场中心,起爆端位于180°方位。数值模拟计算与实验“背靠背”进行,一方面可以为实验测试提供预估,另一方面也确保了软件置信度验证的客观性。
图6 中给出了数值模拟与实验的冲击波压力-时间曲线对比。可以看到,对于长药柱周围不同方位的冲击波压力,数值模拟得到的曲线形状、变化趋势、幅值均与实验测量结果定量可比。个别测点(如P3 和P4)处的冲击波到达时间略有滞后,这应该是由于传感器在水下安装的位置存在一定偏差,相应的冲击波峰值压力较数值模拟结果的略低,这也符合冲击波的传输衰减规律。冲击波到达时间、峰值压力、持续时间和冲量的定量对比见表1,大部分模拟结果与实验结果的绝对误差在10%以下。总体上看,数值模拟结果较好地反映了长药柱水下爆炸周围冲击波的压力分布特征。
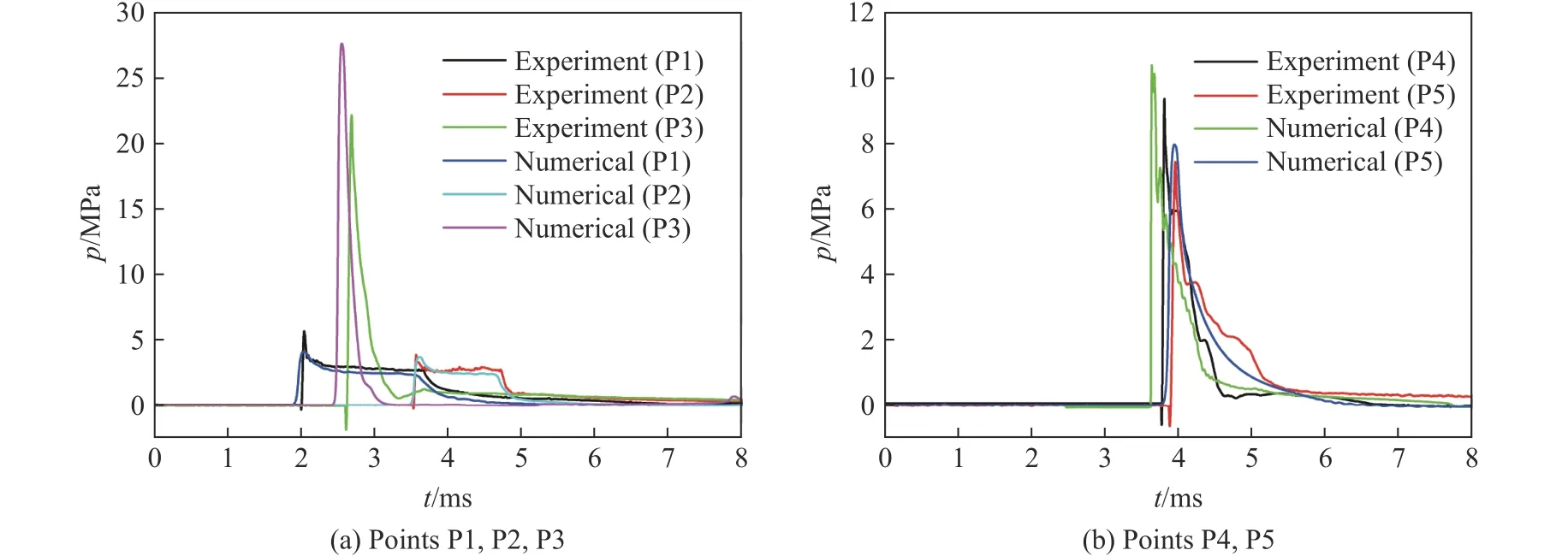
图6 冲击波压力-时间曲线的实验与模拟结果对比Fig. 6 Experimental and numerical pressure-time curves
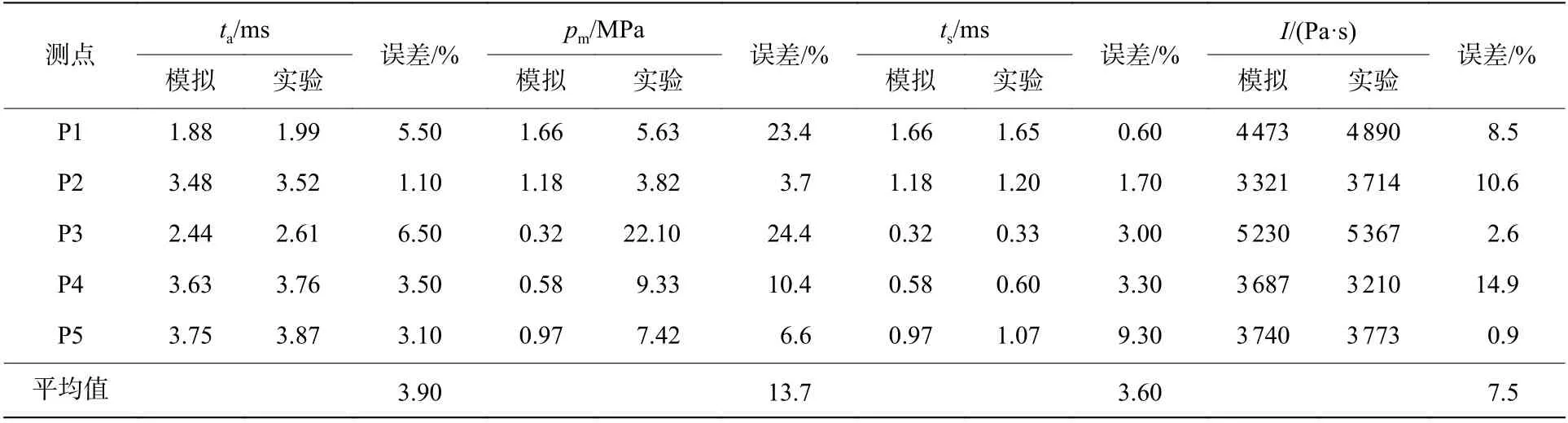
表1 冲击波关键特征量定量对比Table 1 Quantitative comparison of shock wave parameters
此外可以看到,对于长径比很大的装药结构,除了冲击波的超压峰值、持续时间呈现出方向性特征之外,其周围流场中的冲量也具有非均匀性的特点,在装药的侧面最高,其他方位则明显较低。这主要是由于装药完成爆轰的时间已经达到了毫秒量级,不能再按照瞬时爆轰模型进行简化。装药形状和起爆方式对水下爆炸压力分布的影响主要在近场,装药在不同部位的爆轰时间和产生的压力均存在着差异,这种差异性在一端起爆的细长形结构装药上体现得尤为明显。装药周围流场中的任一点的冲击波压力持续时间近似等于最后到达的冲击波与最先到达的冲击波的时间差,即冲击波的脉宽主要与炸药的爆速和冲击波在水中的传播速度有关,冲击波的压力在这段时间内存在多波头叠加效应。随着爆轰波的传播,在水中形成的冲击波将在起爆端一侧已经被压缩的水中传播,这大大增加了问题的复杂性。因此,有必要结合数值模拟结果进一步分析装药形状对水下爆炸能量输出的影响。
2.3 水下爆炸能量输出规律
基于数值模拟结果,并结合实验数据,可以进一步分析细长装药的水下爆炸能量输出规律。图7为长药柱水下爆炸冲击波传输过程中,不同时刻压力分布的数值模拟结果(布局参照图4)。可以看到,在装药两端,冲击波的压力分布有拉宽的现象,即冲击波的持续时间增加,而在装药侧面冲击波的压力区域则较为集中,压力也更高。这些现象表明,起爆位置和装药形状对水下爆炸冲击波的影响是显著的。
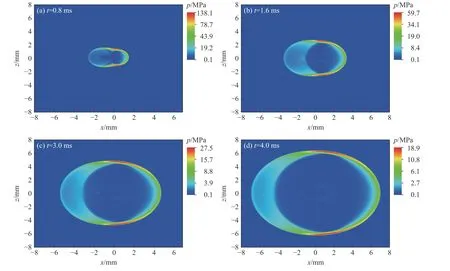
图7 水下爆炸冲击波的压力传播过程Fig. 7 Propagation of underwater explosion shock wave
从数值模拟结果可以看出,水下爆炸能量输出结构与起爆位置和装药形状有关。长药柱从左端起爆后,爆轰波沿着装药轴向以炸药爆速传播,在这个过程中装药各部分被依次引爆并在周围流场中形成冲击波,对于不同方位的测点,装药各部分的爆炸冲击波都将形成叠加效应。进一步分析发现,通过几何近似可以对冲击波压力持续时间进行估算。按照图4 的布局,对流场中的某一固定测点,最先到达冲击波与最后到达冲击波的时间差,近似等于该测点处冲击波的持续时间:

式中:为装药起爆端与测点间的距离,为装药另一端与测点间的距离,为水中冲击波速度,为炸药爆速。
计算的冲击波持续时间与数值模拟和实验结果对比见表2,冲击波持续时间在装药180°方位最长,在90°方位最短,在0°方位介于前两者之间,近似计算的冲击波压力持续时间与实验和数值模拟结果基本一致。因此,在炸药爆速和冲击波速度一定的情况下,冲击波压力的持续时间由测点位置和装药长度两个因素共同决定。
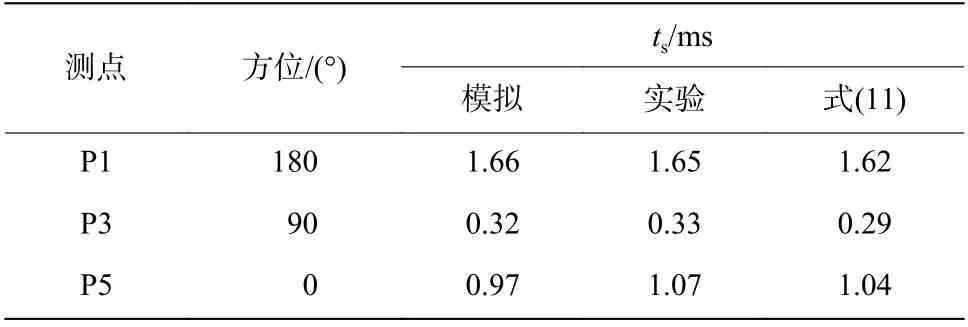
表2 冲击波持续时间对比Table 2 Comparison of shock wave duration
式(11)可作为第1 节中冲击波压力调控方法中约束函数的一个重要约束,用于4 个优化参数中装药长度的确定。当选取好需要等效的冲击波持续时间范围后,即可计算出装药的长度。
3 调控方法的设计验证
以TNT 当量= 1 000 kg、爆距= 100 m 的水下爆炸冲击波压力曲线作为原型,按照第1 节中建立的冲击波压力调控方法,设计与该原型等效的冲击波压力调控方案,然后采用数值模拟对设计的方案进行验证。
针对原型冲击波设计了2 种冲击波压力调控方案,具体参数见表3。冲击波的等效时间取为1.53,3.06 ms,分别对应于原型冲击波持续时间的1 倍和2 倍,用于证明冲击波压力不仅可控,而且可调。

表3 水下爆炸冲击波压力调控方案Table 3 Control design schemes of underwater explosion shock wave pressure
图8 中给出了装药起爆端一侧两种装药方案的冲击波与原型冲击波的压力曲线对比。按照设计的调控方案,只需要几千克TNT 当量的装药,就能在局部方向形成与原型冲击波匹配的压力波形。原型冲击波的持续时间=1.53 ms,根据优化设计的结果,除了峰值压力之外,装药方案1 的冲击波压力在0~范围内与原型冲击波吻合良好,装药方案2 的冲击波压力在0~2范围内与原型冲击波吻合良好。这样就可以通过细长装药起爆方式和装药结构的调控,实现小当量装药冲击波压力与原型大当量水下爆炸冲击波等效的目标。
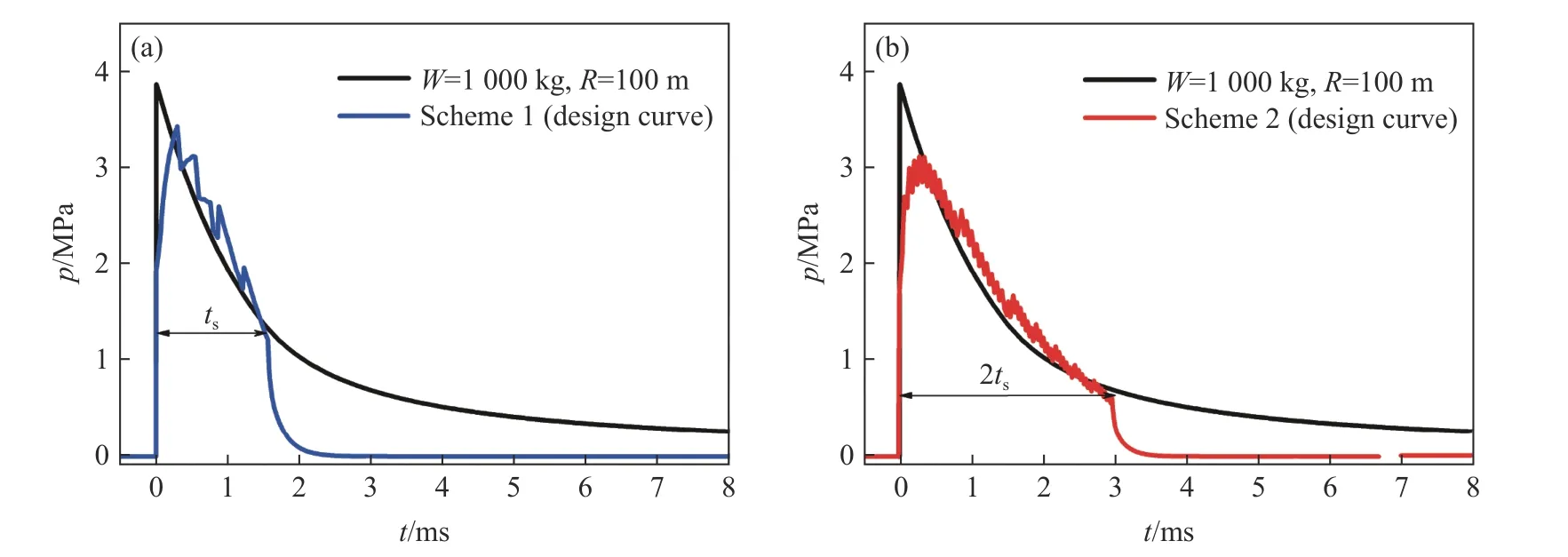
图8 方案1 和方案2 冲击波压力设计结果与原型对比Fig. 8 Comparison of shock wave pressure between the design and prototype curves
采用软件对上述设计方案进行数值模拟验证,计算模型的网格和材料参数与2.2 节中保持一致。图9 中给出了两种装药方案冲击波压力的数值模拟结果与原型冲击波压力曲线的对比。可以看到,根据数值模拟结果,装药方案1 的冲击波压力在0~范围内与原型冲击波基本吻合,装药方案2 的冲击波压力在0~2范围内与原型冲击波基本吻合。这说明本文中建立的水下爆炸冲击波压力调控方法是可行的,依据该方法所设计的装药方案,能够根据需要在一定的时间范围内,实现对大当量水下爆炸冲击波压力的等效。
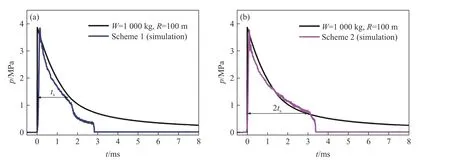
图9 方案1 和方案2 的冲击波压力数值模拟结果与原型对比Fig. 9 Comparison of shock wave pressure between the results of numerical simulation and prototype
4 结 论
建立了一种可用于水下爆炸冲击环境实验的冲击波压力调控方法,并通过了国产自主冲击波数值模拟软件的验证,研究了长药柱水下爆炸能量输出规律,得到以下结论:
(1) 起爆位置和装药形状对水下爆炸冲击波的影响是显著的,在炸药爆速和流体介质一定的条件下,长药柱水下爆炸冲击波压力的持续时间由测点位置和装药长度两个因素共同决定,可通过几何近似计算确定;
(2) 基于细长装药结构建立的水下爆炸冲击波压力调控方法,能够根据需要形成与真实战斗环境等效的水下爆炸冲击波,为舰船结构及设备抗水下爆炸冲击研究提供了一种有效的实验方法;
(3) 本文中建立的水下爆炸冲击波压力调控方法只考虑了对冲击波载荷的等效,没有考虑气泡载荷的等效,因此适用于冲击波占主导的冲击环境问题。
