基于林滋泰德-庞加莱法的达芬系统的求解
2022-09-16莘智侯瑾蓉
莘智,侯瑾蓉
(内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)
1830年,泊松在研究单摆的振动时,提出将非线性系统的解按小参数ε的幂次展开的近似计算方法称为摄动法或小参数法[1]。1892年,林滋泰德为了消除在天文学中利用正规摄动法求近似解时出现的久期项问题,最先提出对正规摄动法进行改进。后来,庞加莱对改进后的方法的合理性进行了证明,故而称为林滋泰德-庞加莱法,它的出现很好地解决了系统共振,即久期项问题。林滋泰德-庞加莱法认为解和系统的激励频率都是ε的未知函数,都要展成ε的幂级数形式,通过确定级数形式中的待定系数,从而求得解析解和频率[2]。本文主要通过林滋泰德-庞加莱法对达芬系统的几种振动求解,得到了精确度较高的近似解析解。
1 达芬系统的自由振动
达芬系统的自由振动动力学方程为[1]

规定初始条件为[2]

此时将该动力学方程的解展开为幂级数的形式

同时,将自由振动的频率ω也展成ε的幂级数形式

将式(4)两边平方,得

将式(3)和式(5)代入式(1),引入新的自变量ψ=ωt,将原来的微分改定义为对ψ的微分,转化为

令等式两边ε相同次幂项的系数相等,可得方程


规定各方程的初始条件为

由零次近似方程(7)和初始条件可以解出

将式(12)的解代入式(8)的右边,可得

为消除方程中出现的久期项,需要令方程右边的cosψ项的系数等于零,于是,可以推导出

这时,在满足此条件的基础上解出x1的值,设

在方程(13)满足初始条件(11)的情况下,可得方程的解为

将式(12)和式(15)代入方程(9)中,整理得

为消除方程中出现的久期项,需要令方程右边cosψ项的系数等于零,导出

此时在满足此条件的基础上,设
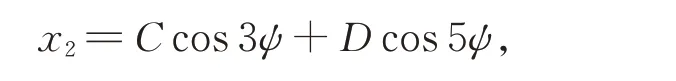
在方程必须满足初始条件情况下,可得方程的解为

将式(12),式(15),式(18)代入方程(10)中并加以整理得

为消除方程中出现的久期项,需要令方程右边的cosψ项的系数等于零,导出

解x3的过程与前面解x1和x2的过程相同,重复操作,可得

由此可得方程(1)的三阶精度的解


以及自由振动频率ω的表达式

2 接近共振的受迫振动
讨论带微弱阻尼的达芬系统接近共振的受迫振动,其动力学方程为

设阻尼项,激励频率以及系统的固有频率均与ε同数量级,令

同样将方程(24)的解设为式(3)的形式,与式(25)一起代入方程(24)中,再令F0=ω20B1,引入新的自变量ψ=ωt,令ε的同次幂项的系数相等,可以导出以下一系列的方程。

由方程(26)可以解出

将此解代入方程(27)中并整理得

为消去共振对系统的影响,需要消除久期项,得到

消去久期项后,可以设方程(30)的解为

把所设方程的解代入方程(30)中,可以解得

将式(32)与式(29)代入式(28)中得

整理得
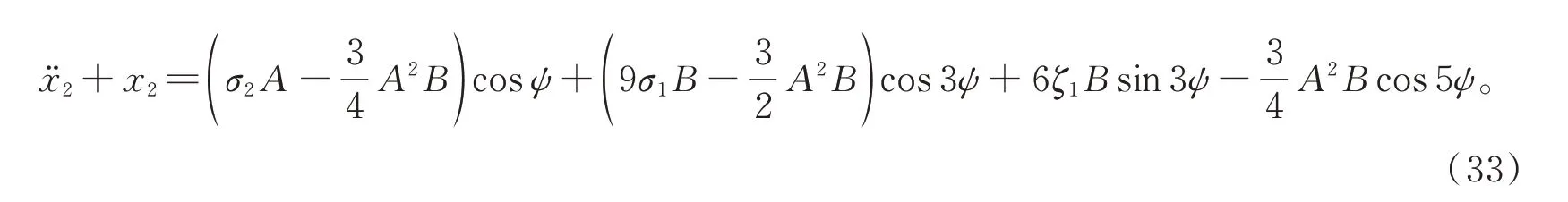
同样地,消去久期项得

设方程(33)的解为

将式(34)代入方程(33),整理后得

由此得

故而方程(24)的二阶近似解便可给出

3 亚谐波共振
讨论亚谐波共振的动力学方程

同样设该方程的解为式(3)的形式,并令

将式(3)与式(39)同时代入方程(38)中,得到

令上式中两边ε的同次幂项的系数分别相等,由此可以推导出一系列的方程。

设方程(41)解的形式为

其中,A13由初始条件决定,将式(44)代入方程(41)中得

将式(44)代入方程(42)中并整理得

为了消除方程中的久期项,得到

或

解出A13的不等于零的解

消去久期项后,设
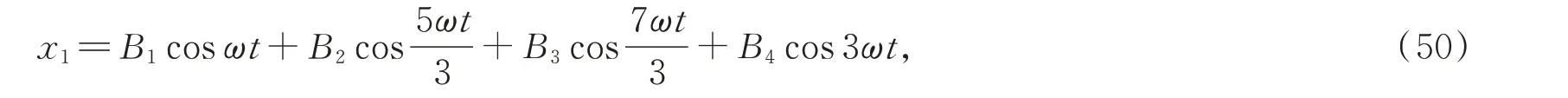
将式(50)代入式(46)中,可以得到
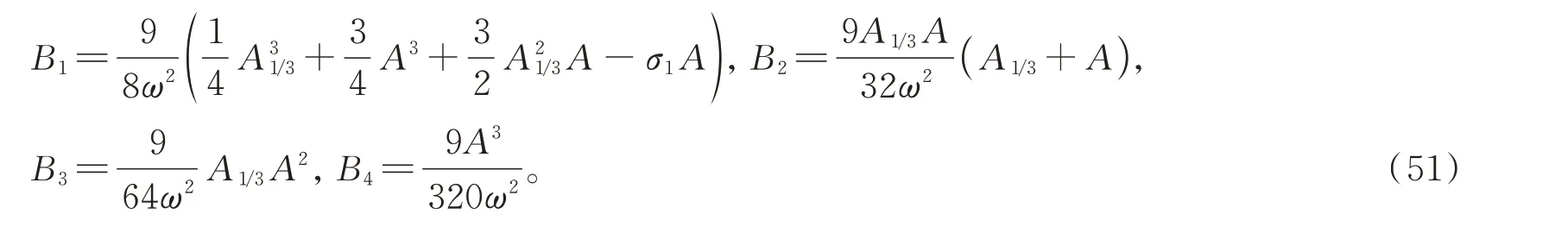
将式(50)和(44)代入方程(43)中,得到

整理后得到

为了消除久期项,得

综上,方程(38)的解可以写成

4 结论
林滋泰德为了消除天文学中的久期项改进正规摄动法,庞加莱为改进的摄动法的合理性进行了数学证明,林滋泰德-庞加莱法和正规摄动法同称为小参数法,也叫PL摄动法。该方法的基本思想是认为非线性系统的固有频率ω并不等于派生系统的固有频率ω0,而应该是小参数ε的未知函数。因此在将基本解展成ε的幂级数的同时,因将频率也写成ε的幂级数,幂级数的待定系数根据周期运动的要求依次确定。本文以达芬系统的自由振动为例,利用林滋泰德-庞加莱法给出了三阶精度的近似解析解,相比较文献[1]从二阶提高到了三阶,进而提高了解的精确程度;讨论了带微弱阻尼的达芬系统接近共振的受迫振动,利用该方法给出了二阶精度的近似解,比文献[1]中的解提高了一阶精度;针对亚谐波共振的情形,将文献[1]中的解的精度由一阶提高到了二阶。利用林滋泰德-庞加莱法对达芬系统的三种不同振动的解求解,实现了非线性振动系统解的精度的提高,进而能够更好地分析非线性系统的运动规律,以及对系统参数和初始条件的依赖关系。但是,得到非线性振动高阶近似解,会增加很大的工作量,因此往往要截断高阶项只保留级数的前面有限项,同时解的最后结果还需要试验来验证。
小参数法是从事理论研究的重要数学工具之一,对于弱非线性问题尤其有作用。理论的研究从实际问题中来,并最终应用到实际问题中,小参数法在基础和应用研究中已被广泛应用于微分方程、轨道力学、非线性振动、固体力学、流体力学等领域[3-6],并且随着科学的不断发展,一定会研究出更多有关小参数的理论,对它的应用也会更加广泛。
