水利设备中二极管钳位型五电平逆变器优化均压算法研究

方 丽

(莒南县岭泉水利服务中心，山东 莒南 276621)

当今世界的能源缺乏与环境污染日益成为人类面临的共同难题。在全球呼吁节能减排的形势下，多电平变换技术已成为高压大功率电力电子技术领域的研究热点[1-2]。多电平逆变器能够以耐压较低的功率器件实现较高电压输出，相对于两电平逆变器具有输出电压等级高、谐波特性好、开关损耗小等优点，因而在高压交流电机调速、分布式发电、静止无功补偿、新型直流输电等领域有良好的应用前景[3]。目前研究得出的多电平逆变器拓扑结构主要有三种：H桥级联型、飞跨电容型和二极管钳位型。其中二极管钳位型多电平逆变器由于无须多个独立直流电源和辅助电路，可靠性较高，相比于其他拓扑结构在应用领域具有更好的发展前景[4]。

由于二极管钳位型的主电路结构和调制算法复杂度随着电平数的增加而急剧上升，目前只对五电平及以下二极管钳位型多电平进行研究[5]。在目前的研究中，二极管钳位型三电平已广泛应用于HVDC、STATCOM、有源滤波等领域。尽管五电平相对于三电平能够输出更高的电压等级以及具备更好的谐波特性，但却存在以下问题：直流侧电容电压不均衡，一个奇数次多电平会逐渐退变为三电平，而偶数次多电平会退变为两电平。目前实现二极管钳位型五电平逆变器均压的主要方法有：为电容分别独立供电；通过外接电路辅助均压；优化SVPWM算法选择合适的冗余矢量均压。相比于前两种方法需要外接设备辅助完成均压，优化算法选择合适的冗余矢量均压的方法更具备经济性，是当前研究的热点。张兴等[6]、赵志宏等[7]分别研究了二极管钳位型五电平逆变器在HVDC和STATCOM中的应用，得出SVPWM算法的均压效果受到逆变器调制比和功率因数的影响，当调制比小于0.5时，可以利用内层较多的冗余矢量实现全功率因数均压，当调制比大于0.5时调制比升高会导致功率因数降低，而当调制比继续升高至1附近时，二极管钳位型五电平逆变器几乎不能输出有功功率。本文将高调制比算法类比于低调制比，完成算法编写，通过仿真验证得出该算法能够实现二极管钳位型五电平逆变器的均压，且具有较好的动态性能。

1 二极管钳位型五电平逆变器拓扑结构

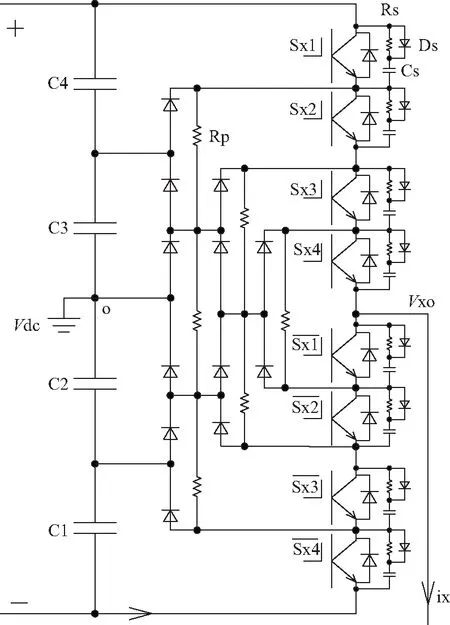
图1 改进二极管钳位型五电平逆变器主电路

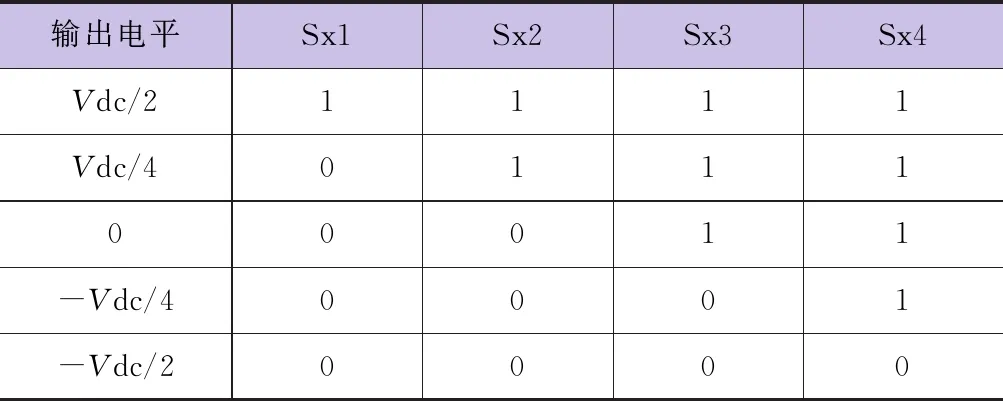
表1 改进二极管钳位型五电平逆变器工作状态

如表1所列，逆变器每相可以输出五种电平(Vdc/2、Vdc/4、0、-Vdc/4、-Vdc/2)，将其定义为编号为0，1，2，3，4五种工作状态，因此三相共有125种工作状态组合，其空间矢量图如图2所示。由图可知，125个开关矢量中61个为有效矢量，剩余的为冗余矢量。

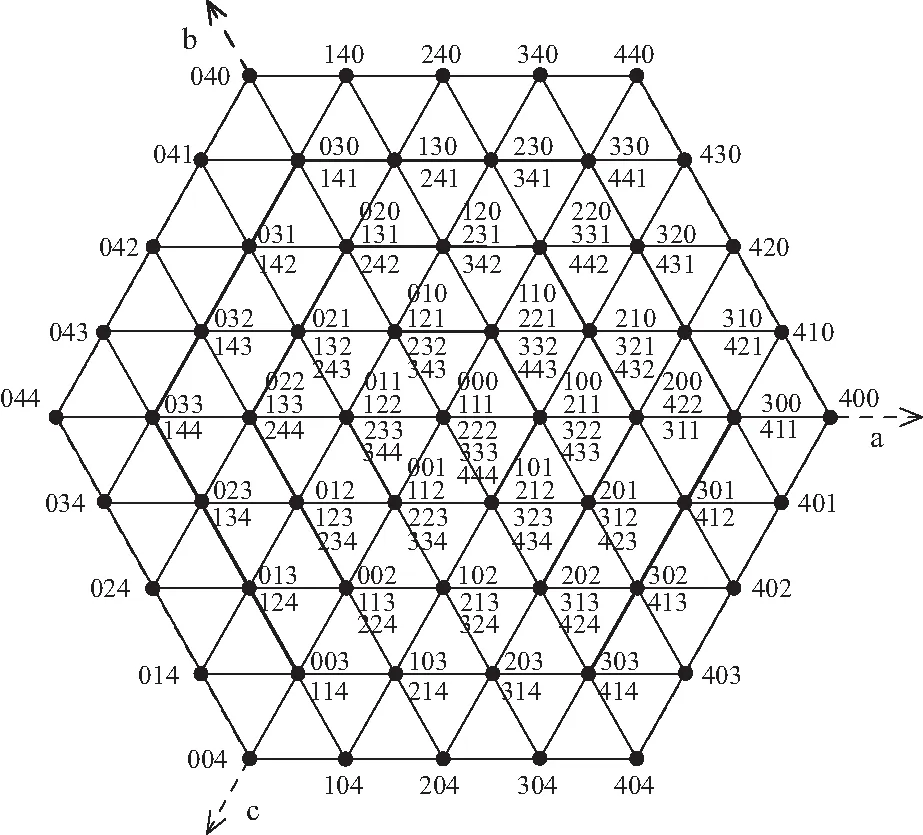
图2 二极管钳位型五电平逆变器空间矢量图

二极管钳位型五电平逆变器空间矢量图由四个正六边形中心嵌套而成，其中绝大部分冗余矢量位于内两层六边形区域内，因此当逆变器调制比较低时，目前大多SVPWM算法均是利用内两层六边形数量众多的冗余矢量进行均压，而随着调制比的增大，冗余矢量个数逐渐减少，其中最外层六边形只有一种状态，冗余矢量个数为零，较少的冗余矢量选择导致直流侧电容均压变得十分困难。

2 二极管钳位型五电平逆变器控制策略

通过观察图2可知，当逆变器的开关序列矢量位于矢量图最内层六边形上时，逆变器仅对一个直流侧电容电压有影响。例如，假设逆变器此时开关矢量为(100)，如图3所示，此时逆变器仅对电容C1进行充放电,控制电流为Ia。当开关矢量位于第二、三、四层六边形上时，逆变器对相邻的2，3，4个直流侧电容电压起调节作用。

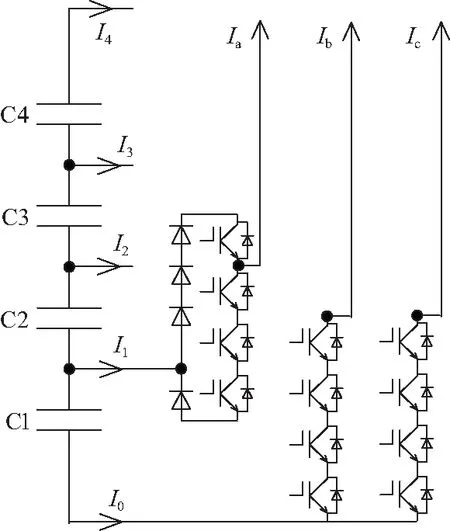
图3 开关矢量(100)主电路工作状态

基于上述原则，本文所采用的SVPWM算法控制将矢量图分为如图4所示两个区域。 内两层六边形即图4深色部分为区域1，本文第三节将介绍区域1部分的相关五电平控制均压算法；外两层六边形为区域2，当参考矢量位于区域2时，此时忽略一些节点将空间矢量图转化成三电平矢量图，即将四个直流侧电容进行成对控制。这样高调制比下的控制关键环节(矢量序列选择，确定最近三矢量)即可采用类比于区域1的三电平SVPWM算法。

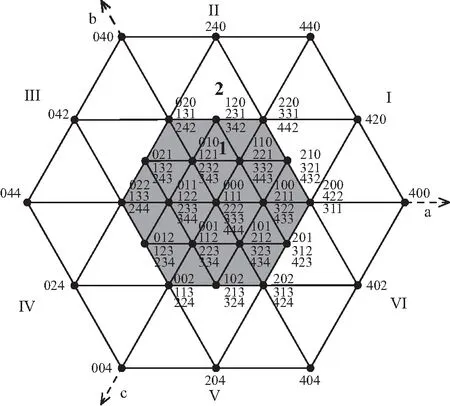
图4 空间矢量图区域划分

3 二极管钳位型五电平SVPWM算法

由于空间矢量图的旋转对称性，我们可以将其分成如图4所示Ⅰ～Ⅵ六个完全相同的扇区。以下有关算法的讨论均以扇区Ⅰ为例，其余扇区的控制均可在算法中通过坐标转换转化为扇区I进行处理。

3.1 区域1部分

扇区I区域1部分由四个三角形组成，将其按如图5所示进行编号。当确定参考矢量Vref所在三角形区域时，该三角形所在的三个顶点即为当前最近三矢量V1、V2、V3。由于三角形在矢量图中的方向不完全相同，当参考矢量位于三角形1，2，4中时，最近三矢量V1、V2、V3如图5(a)所示；当参考矢量位于三角形3中时，最近三矢量V1、V2、V3如图5(b)所示。

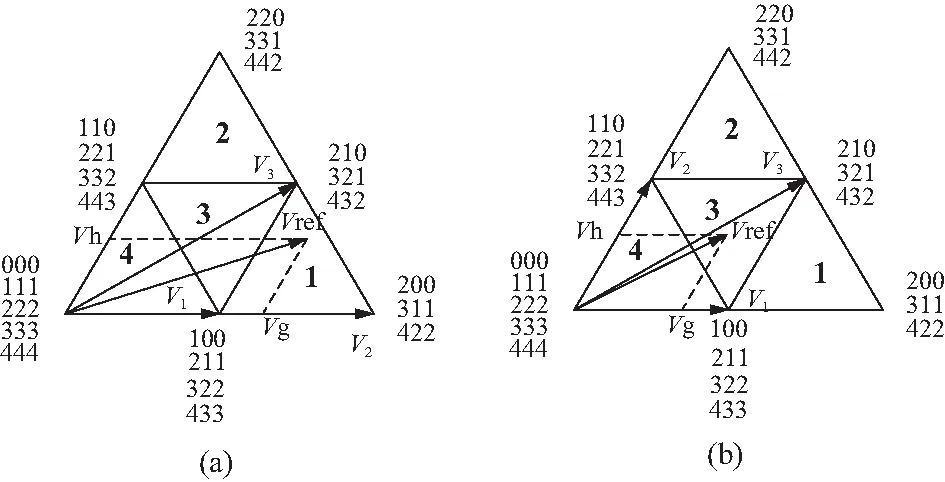
图5 扇区I区域1空间矢量图

由七段式矢量序列规则可知，当参考矢量位于三角形1或2时，矢量序列起始点唯一(100/211/322/433为三角形1起始点，110/221/332/443为三角形2起始点)；当参考矢量位于三角形3或4时，矢量序列起始点有2种选择(100/211/322/433和110/221/332/443均可作为三角形3或4的起始点)。因此按此分类后，我们仅需对三角形1和3进行分析。

3.1.1 三角形1区域

可是林师父自己画风，却要我们画水！他说：“平远细皱，起起伏伏，这是画匠们的画法，你们要学水奔湍巨浪，随石曲折，随物赋形，画出水的神气。画好了水，才画得出风，画得出光。”

在三角形1中，矢量序列起始点共有100、211、322和433四个开关序列，由图3类比可知这四个序列分别对电容C1、C2、C3和C4电压起调节作用。该三角形区域内存在的七段式序列及其控制的电容如表2所列。

表2 三角形1矢量序列

由图3可知，三角形1中的均压控制电流为Ia：当Ia大于0时，此时逆变器对所控制的电容放电；当Ia小于0时，此时逆变器对所控制的电容充电。为了达到电容电压均压的效果，应该利用控制电流的调节作用，对当前电压较低的电容充电或对电压较高的电容放电。另外，表2所列出的七段式矢量序列均同时控制相邻的2个电容。因此，控制算法核心思路总结如下：

a.判断当前控制电流方向，确定此时对电容的调节方式为充电还是放电。

b.确定当前的调节方式为充(放)电后，选择当前电压最低(高)的电容为目标控制电容。

c.判断目标控制电容相邻电容的电压，选择其为第二个控制电容，根据选择的2个控制电容查找表2确定矢量序列。

举例分析，假设当前控制电流Ia大于0，电容电压状态为Vc2>Vc3>Vc4>Vc1，由于此时控制电流对电容电压放电，因此应该选择电压最大的电容C2。此外，C2相邻电容的电压状态为Vc3>Vc1，因此应该选择 C2和C3为控制电容，选择矢量序列为211-311-321-322-321-311-211。

依据以上原则，表3按各电容分类列出了三角形1内所有情况下的矢量序列选择，其中Vc1至Vc4分别代表四个直流侧电容的电压，Vmax为四个直流侧电压的最大值，Vmin为四个直流侧电压的最小值。

表3 三角形1矢量序列选择

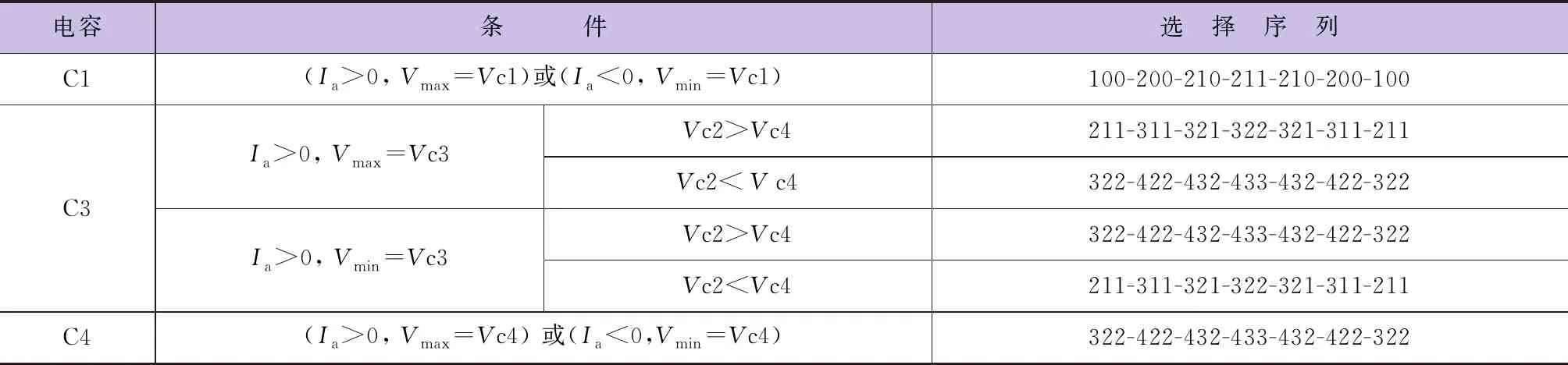
续表

在三角形3中，存在2个矢量序列起始点，其控制电流分别为Ia和-Ic，我们分别定义其为起始点1和起始点2，首先应确定1和2哪个为矢量序列起始点。文献[7]提供了一种判断矢量序列起始点对于电容电压调节作用强弱的方法，具体如下：

设起始点1一个周期内作用时间为t1，起始点2作用时间为t2。如果|Ia×t1|>|Ic×t2|，则起始点1具有更好的电压平衡能力，应选择其为矢量序列起始点，否则应选择起始点2为矢量序列起始点。

起始点确定后，其余步骤与3.1.1中三角形1区域内相同。

3.2 区域2部分

在区域2中，我们将直流侧电容C1和C2，C3和C4进行联合控制，这样区域2中的均压控制就转换为三电平SVPWM控制。此时区域2的空间矢量图如图6所示，共分为三角形1，2，3三个区域，其中三角形1和2中仅有1组矢量序列，三角形3中有2组可选择的矢量序列。

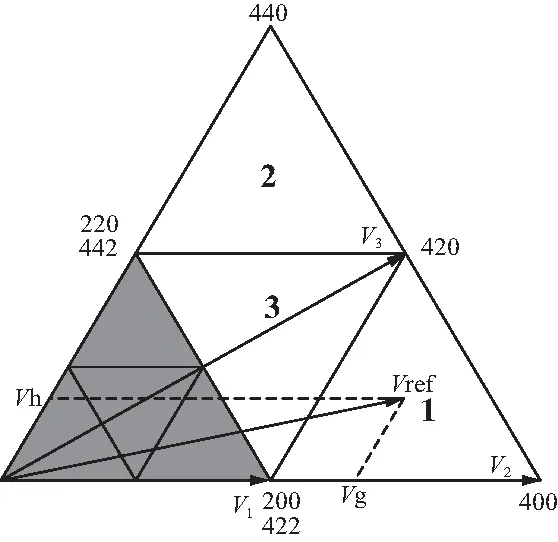
图6 扇区I区域2空间矢量图

在三角形3中，由于存在2组七段式矢量序列：200-220-420-422-420-220-200和220-420-422-442-422-420-220需要进行选择。这里采用与3.1.2中相同的方法：如果|Ia×t1|>|Ic×t2|，则选择200-220-420-422-420-220-200矢量序列，否则应选择220-420-422-442-422-420-220矢量序列。

4 仿真验证

为验证本文所提出的二极管钳位型五电平逆变器改进SVPWM算法的有效性，在Simulink仿真平台下以图1所示电路拓扑为基础进行仿真验证。仿真参数设置如下：直流侧电压400V，开关频率2kHz，电容器C1、C2、C3、C4的电容值均为6800μF，负载电阻10Ω，负载电感20mH。

设置调制比为0.2，此时参考电压位于区域1内，图7为调制比为0.2时的各项仿真参数波形图。可以从图上看出，直流侧电容电压的波动均在99.8～100.2V之内，达到了理想的均压效果。

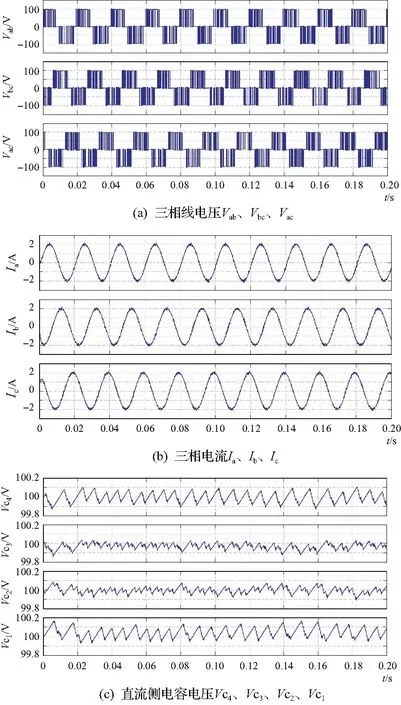
图7 调制比m=0.2仿真波形

设置调制比为0.53，此时参考电压位于区域2内，图8为调制比为0.53时的各项仿真参数波形图。由图可知，直流侧电容电压纹波在1.2V以内，均压效果较为理想。

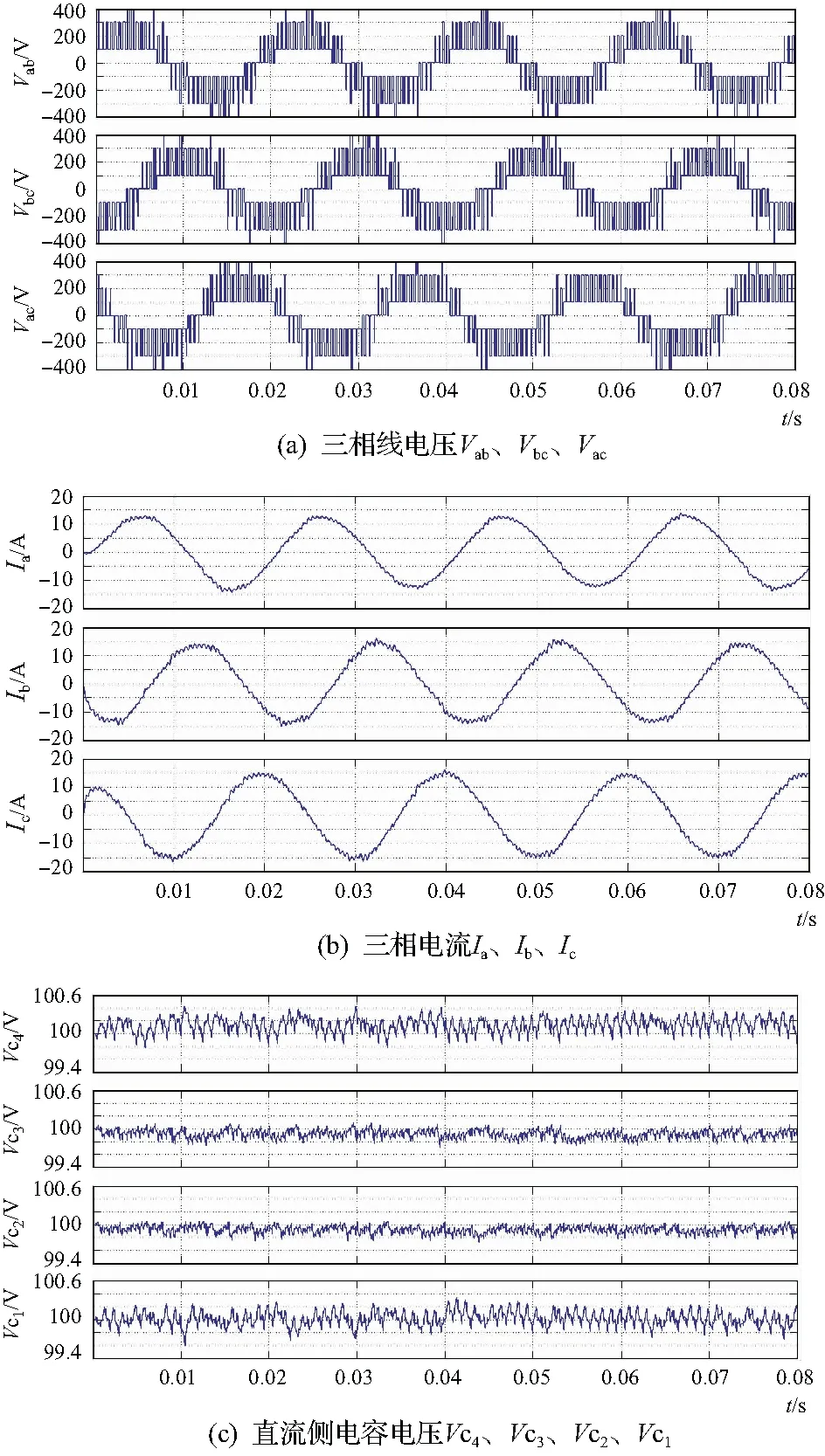
图8 调制比m=0.53仿真波形

5 结 论

随着近年来高压大功率电力电子技术的不断发展与应用，五电平的相关研究已成为电力电子领域的研究重点之一。本文在总结与归纳现有研究成果的基础上，采用一种改进型的SVPWM算法，通过利用七段式矢量序列对于电容电压的调节作用，实现了二极管钳位型五电平逆变器的直流侧均压，最后通过仿真验证了该算法的正确性及有效性。