一维波动方程的计算模拟
2022-09-16斯小琴陈大伟
斯小琴,陈大伟①
(1.安徽建筑大学城市建设学院 基础部,安徽 合肥 238076;2.中国科学技术大学 物理学院,安徽 合肥 230026)
0 引言
波动方程主要描述自然界中的各种波动现象,包括横波和纵波,例如光波、声波和水波.它也是一种重要的二阶线性偏微分方程,是双曲形偏微分方程的典型代表,出现在不同领域,如物理学、流体力学和声学等领域[1-2].历史上许多著名的科学家在波动方程的研究上都做出贡献,如达朗贝尔、欧拉、伯努利和拉格朗日等[3].
在这类波动方程的研究过程中,仅仅有方程还不足以完全确定具体的物理过程,即不能完全确定方程的解.因为任何一个波动过程,在某一时刻的振动状态不仅始终与此刻之前的状态即初始时刻的状态有关,还与两端所受的约束即端点处的物理条件有关,也就是说具体的物理过程与初始条件及边界所受的外界作用均有关[4-7].在实际求解方程时,除一些特殊的情况下,如涉及的物体几何形状比较简单时,可以方便地求出其精确解.其他情况由于实际物理问题的复杂性,往往很难得到其精确解.因此,研究该类方程的数值解就显得比较重要.
求解波动方程数值解的方法很多,常用的求解方法有分离变量法[8]、行波法[9]、格林函数法[10]、积分变换法[11]等,而最常用也较为成熟的数值解法是有限差分法[12-15],其计算快速、精度较高、适用性强、容易在计算机上实现,是使用范围最广的一种数值方法,在数值模拟研究中受到广泛的应用.它的基本思想是将问题的定义域进行网格离散化,将每一网格处的导数由有限差分近似公式代替,从而把求解偏微分方程的问题离散化成差分格式,进而求出数值解.
本文利用有限差分格式,通过基本办公软件EXCEL迭代[16],Origin模拟数据,得到有初始条件和边界条件的混合问题的一维波动方程的波动图,从图像中分析波动的性质,结果直观、形象,方法简单、实用.
1 模型与方法
考察一根长为l拉紧的均匀、柔软而有弹性的弦,弦的左右两端均为自由端,且施加不同频率的外力R1(t)和R2(t),其在平衡位置附近作垂直方向上的微小横振动时,各点的运动规律满足的一维波动方程如下:

其中:u=u(x,t)表示弦上x点在t时刻沿垂直于x方向的位移,a是振动的传播速度,f(x,t)为弦在振动过程中受到的外力,u(0,t)=R1(t),u(l,t)=R2(t)为边界条件,u(x,0)=φ(x)为弦振动时的初始位移,为初始速度,R1(t)、R2(t)、φ(x)、φ(x)均为已知函数.
利用有限差分法解上述一维波动方程的数值解问题.分别取Δx=h,Δt=τ将空间和时间进行离散化(h,τ分别称为沿空间方向和时间方向的步长),即将空间和时间分别分割成m,n等份,可得网格节点坐标如下:

根据有限差分方程的构造方法,可得一维波动方程式(1)的差分格式为

其中ukj=u(xj,tk)表示节点(j,k)处的函数.引入网比,则式(3)变为

由式(4)可知,若求k+1时刻的振动位移可由之前的k和k-1时刻的振动位移直接获得.值得注意的是,s2≤1为该差分格式的稳定和收敛条件,中心阶段误差[13-14]为ο(h2)+ο(τ2).
对式(1)的初始条件用向前差商表示有:

即

2 数值模拟结果及分析
考虑一实际问题,一根长为1 m的弹簧,一端固定,另一端在外力作用下做周期T=1 s的振动,该点的振动方程为u(1,t)=sin 2πt,其振动的传播速度a=1 m/s,在初始时刻t=0时振动的初始位移和初始速度均为0,考察该弹簧上各点在各时刻的振动情况.
由描述可知,该问题为既有边界条件又有初始条件的一维混合问题,即为如下方程:

取τ=0.05 s、h=0.05 m,由式(4)得其差分方程为:

由式(6)得初始条件为

通过所取的时间步长τ=0.05 s和空间步长h=0.05 m可将时空平面分割成21×21个时空节点.在基本办公软件EXCEL中以第1行表示空间节点,1 m的空间长度可表示为0、0.05、0.1、…、0.95、1 m共21个节点;以第1列表示时间节点1 s的时间长度可表示为0,0.05、0.1、…,0.95、1 s共21个节点.在EXCEL第2行和第3行中输入式(9)的初始条件数值,在第2列和最后一列中输入式(7)中的边界条件数值,最后在节点(0.05,0.1)处编写式(8),利用EXCEL中的下拉迭代计算功能,很快得到弹簧上各点在各时刻的振动位移数值.为直观地观察和理解波的振动情况,运用Origin画图软件将数据模拟成图形.图1给出弹簧上所有质点的位移随时间变化图,x轴表示各质点离坐标原点的距离,从图1很容易观测到各质点各时刻的振动位移.因弹簧的一端固定,另一端在外力作用下做周期振动,是由末端的振动慢慢带动前面质点的振动,这种现象在图1中可以看出,开始时的振动位移都是0,即没有振动.

图1 弹簧上所有质点的位移随时间变化图
为更详细地观察各质点的振动情况,可将图1各质点各时刻的振动位移三维图进行分解为振动位移随坐标的二维变化图(图2),即图1沿着x方向的图形和振动位移随时间的二维变化图(图3),即图1沿着t方向的图形.
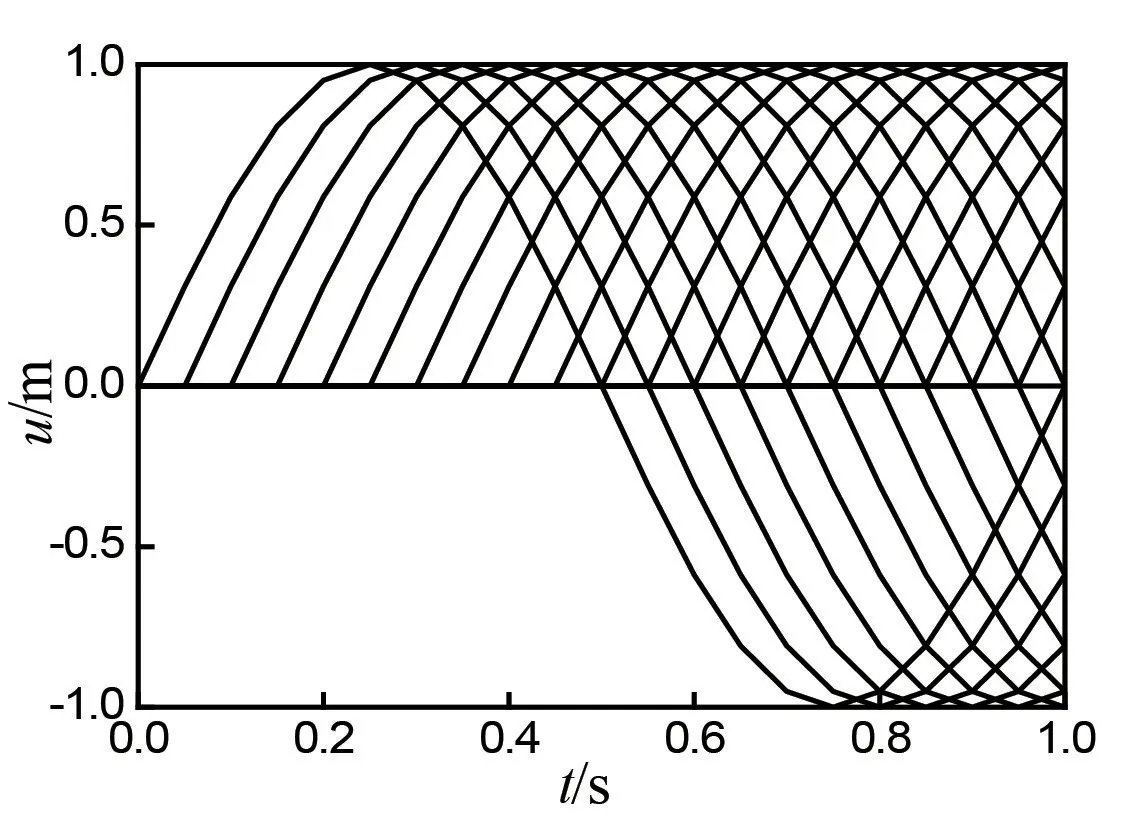
图3 弹簧上空间坐标x每隔0.05 m时各质点的振动位移随时间变化图
图2中分别给出t=0,1/4T,1/2T,3/4T,4/5T和T各时刻对应的振动位移随坐标的动态变化图.从图2看出,开始时各质点都在平衡位置均未振动,随着时间的推进,末端质点由于受外力作用发生周期性的振动,同时带动弹簧上相邻质点的振动,当末端质点完成自己的一个完整的周期振动,弹簧上就有一个完整的正弦波形出现.

图2 弹簧上各点在固定t时刻的振动位移随坐标变化图
图3是空间坐标每隔0.05 m时的振动位移随时间变化图形,开始时为一横轴上的一条线,即起始各点都在平衡位置均未振动,末端振动带动相邻点依次振动.
3 结论
本文利用有限差分法表示波动方程及其初始、边界条件的差分格式,借助基本办公软件EXCEL的下拉迭代计算功能,方便、快速地计算出波动方程的数值解,通过Origin将大量数据绘制成图,直观地得到波动方程各点的振动情况.对于不同初始、边界条件下或有非齐次项(fx,t)时,不同波动方程的求解此方法同样适用.
有限差分法不仅可以解决形式简单的容易求解解析解的波动方程,对于复杂的边界条件不易求解解析解的波动方程,用差分法求数值解更简单方便.而基本办公软件迭代、Origin模拟图形,过程方便、快捷、简单.此方法在解决实际问题中有一定的使用和参考价值.
