信赖域子问题的一种非精确光滑牛顿法

凌文静，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北 235000）

0 引言

信赖域方法最早由Powell［1］提出，因其具有较为理想的全局收敛性和稳定性备受广大学者的青睐.信赖域算法的基本思想是：在给定的信赖域半径内，以当前迭代点为中心做一个闭球区域，在此区域内求解信赖域子问题来确定迭代步dk，产生新的迭代点.也就是说在每次迭代时都需要求解信赖域子问题，所以信赖域方法中信赖域子问题的求解是算法实现的关键.考虑信赖域子问题

其中gk=∇f(xk)，Bk为Hesse矩阵∇2f(xk)的第k次近似，Δk为信赖域半径，‖‖·是Euclidean范数.

常见求解信赖域子问题的方法是折线法［2］、特征值分解法［2］、共轭梯度法［3-5］以及精确光滑牛顿法［6］等，这些方法各有优点和不足，如特征值分解法对于二维或低维子空间问题算法有效，折线法当下降方向不靠近牛顿方向时下降速度较慢，精确光滑牛顿法需要在迭代点靠近最小值时才能保证收敛性等.本文提出一种求解信赖域子问题的非精确光滑牛顿法，当Hesse矩阵∇2f(xk)的第k次近似矩阵Bk为对称正定矩阵时，该方法具有迭代次数少、迭代时间快等特点，还可推广到求解高维子空间的信赖域子问题.受文献［7-8］光滑函数的启发，本文提出一个新的光滑互补函数，在此基础上，应用非精确牛顿法求解信赖域子问题.

1 基础知识

通过下述引理将求解信赖域子问题（1）转化为求解互补问题.

引理1［9］d是子问题（1）的解当且仅当

并且Bk+λI是半定矩阵.

定义1［9］设向量值函数F:Rn→Rm，x∈Rn，若存在Lipschitz常数L＞0，使得对任意的y∈Rn，满足‖F(x)-F(y)‖≤L‖x-y‖，则称F在x处是Lipschitz连续的.若对任意的x,y∈Rn都成立，则称F在Rn内是全局Lipschitz连续的.

定义2［9］满足以下三条性质的函数称为V上的范数‖·‖:V→R

（1）正定性：‖x‖≥0,∀x∈V且‖x‖=0⇔x=0；

（2）正齐次性：‖αx‖=|α|‖x‖,∀α∈R,∀x∈V；

（3）三角不等式：‖x+y‖≤‖x‖+‖y‖,∀x,y∈V.

定义3［8］对于非光滑函数g:Rn→Rm，含有参数μ的函数gμ:Rn→Rm满足下列性质

（1）对于任意的μ＞0，gμ是可微的；

定义4［9］设算法产生的点列{xk}收敛于极小点x*，并且，则称该算法是局部二次收敛的.

定义5［10-11］设H:Rn→Rm是局部Lipschitz连续的，0＜p≤1.如果对∀h→0和D∈∂H(x+h)，有Dh-H′(x;h)=O(‖‖h1+p)，则称H是p-阶半光滑，特别是p=1时称为强半光滑.

引理2［12］假设函数F:Rn→Rm在x处是p-阶半光滑，函数G:Rm→Rn在F(x)处是p-阶半光滑，则复合函数H=G◦F在x处是p-阶半光滑.

2 光滑函数及性质

一个经典的光滑函数是著名的Chen-Harker-Kanzow-Smale（CHKS）光滑函数［13］，即

本文中构造函数φ:R+×R×R→R：

定理1令(μ,a,b)∈R+×R×R，φ(μ,a,b)由式（3）定义，则下述结论成立

（i）φ(μ,a,b)是φ(0,a,b)的一个光滑函数；

（ii）φ是全局Lipschitz连续且当μ＞0时强半光滑，φ在(μ,a,b)∈R+×R×R是连续可微的，且其雅可比矩阵为

证明（i）令，则式（3）可写成φ:=(1+μ)(a+b)-K.对K求偏导有，

则 对 于 任 意μ＞0，K(w)的 偏 导 在 任 意(μ,a,b)∈R+×R×R都 存 在，φ(μ,a,b)的 偏 导 在 任 意(μ,a,b)∈R+×R×R也存在，于是φ(μ,a,b)在定义域内每一点都可微，又，则由定义3可知，φ(μ,a,b)是φ(0,a,b)的一个光滑函数.

（ii）先证明φ是全局Lipschitz连续的.

不妨设a＞b，对任意μ＞0，有

对∀(μ,a1,b1),(μ,a2,b2)∈R+×R×R，结合式（5）～（6）有

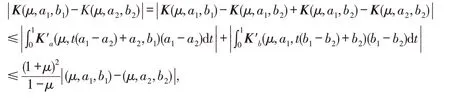
即

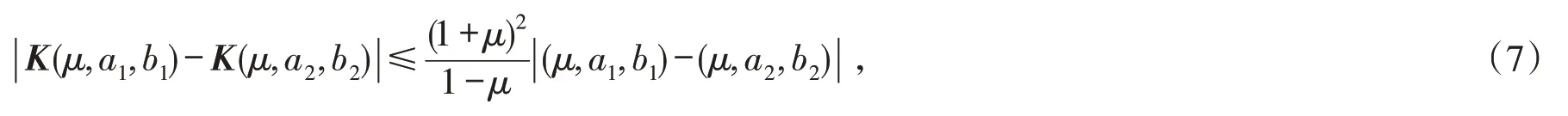
由式（7）有

由（i）知，φ在点(μ,a,b)∈R+×R×R连续可微，注意到φ(μ,a,b)=φCHKS(μ,(1+μ)a,(1+μ)b)，由文献［14］可知，当μ＞0时，φCHKS是强光滑的，又函数(1+μ)a和(1+μ)b也是强半光滑的，由引理2知φ是强半光滑的.

下证式（4）成立.对于任意z=(μ,a,b)∈R+×R×R，通过式（5）及求微分的链式法则可知

即式（4）成立.令z=(μ,λ,d)∈R+×R+×Rn.由引理1可知问题（1）等价于

其中

3 非精确光滑牛顿法及收敛性

基于光滑函数（3），将信赖域子问题的互补模型（2）转化为等价方程组式（8），给出求解信赖域子问题的非精确光滑牛顿法.

算法3.1（非精确光滑牛顿法）

步骤0任取z0=(μ0,λ0,d0)∈R+×R+×Rn，选取常数δ∈(0,1)，σ∈(0,1)，γ∈(0,1)，使得γμ0＜1，另取序列{ηk}满足ηk∈[0,η]，这里为一个常数，k:=0.

步骤1若‖H(zk)‖=0，则终止.

步骤2由下式计算Δzk=(Δμk,Δλk,Δdk)：

这里βk=β(zk):=γ‖H(zk)‖min{1,‖H(zk)‖}，rk∈Rn满足‖rk‖≤ηk‖H(zk)‖.

步骤3让λk为1,δ,δ2,…中使下式成立的最大值：

步骤4令zk+1:=zk+λkΔzk，k:=k+1，返回步骤1.

定理2令若Bk对称正定，则对

任意的z=(μ,λ,d)∈R+×R+×Rn,雅可比矩阵H′(z)是非奇异的，且算法3.1中的步骤2和步骤3是适定的.

证明任取μ＞0，令Δz=(Δμ,Δλ,Δd)∈R+×R+×Rn.假设

只需要证Δz=0.

由式（9）、式（10）可得

于是-(1-θk)(Bk+λI)Δd=2(1+θk)ddTΔd.若Δd≠0，则-(1-θk)ΔdT(Bk+λI)Δd=2(1+θk)(dTΔd)2，由于0＜θk＜1，Bk+λI半正定，等式左边小于0，等式右边大于0，等式两边不相等，矛盾.于是Δd=0，从而Δλ=0，故Δz=(Δμ,Δλ,Δd)=( 0,0,0).即证雅可比矩阵H′(z)是非奇异的.步骤2和步骤3适定性的证明与参考文献［10］中的证明类似，在此不再赘述.

定理3［8］设函数H单调连续可微，且z*=(μ*,x*,y*)是算法3.1所产生的迭代点列{zk}的一个聚点，则

（i）z*=(μ*,x*,y*)是H(zk)=0的一个解；

（ii）如 果 所 有 的V∈∂H(z*)可 逆，且∇HLipschitz连 续，则{zk}局 部 二 阶 收 敛 于z*，即

证明与文献［8］中定理4证明类似.

4 数值实验

针对无约束优化的信赖域子问题（1），本节对不同的信赖域半径，给出算法3.1的数值结果，并与双割线折线法［15］进行数值比较，比较结果列在表1和表2中，其中Δ表示信赖域半径，qk(d)表示函数值，DSD表示双割线折线法，ISN表示非精确光滑牛顿法，qDSD-qISN表示使用双割线折线法与非精确光滑牛顿法得到的最优解的差值，该差值越大，表明非精确光滑牛顿法越好.为进一步观察非精确光滑牛顿法的性能，表3列出部分Δ下迭代次数k与CPU时间（单位：s），其中CPU时间和迭代次数均是多次求解后的平均值.算法中参数取值为：

测试函数均来自于文献［15］，如下：

从表1、表2和表3结果可以看出，本文所设计的算法稳定可靠，且当信赖域半径较小（其中Function1：Δ≤9，Function2：Δ≤4.）时非精确光滑牛顿法（ISN）比双割线折线法（DSD）更接近精确解，所需迭代次数和CPU时间很少，说明文中所设计的算法适合求解信赖域子问题.

表1 Function1与双割线折线法的数值结果

表2 Function2与双割线折线法的数值结果

表3 部分Δ下运行的结果