战术自组网下非平稳信道测量与建模

谢诗昂 张晓瀛 孔凌劲 王 玲 魏急波 刘永胜 林乐科

（1.湖南大学电气与信息工程学院，湖南长沙 410082；2.国防科技大学电子科学学院，湖南长沙 410073；3.中国电波传播研究所，山东青岛 266107）

1 引言

战术自组织网络（tactical mobile ad hoc network，TacMAN）是移动自组织网络（mobile Ad Hoc net⁃work，MANET）在军事通信领域的重要应用，是一种无中心结构、无固定基础设施的无线移动通信网络，具有显著的灵活性、可靠性和便携性，能在复杂紧急的情况下实现快速部署。与传统的蜂窝网络相比，TacMAN 具有如下特点：（1）战场环境的推进和通信节点的移动可能导致信道统计特性呈现时变性；（2）收发天线临时架设，高度受限，导致发射机和接收机可能被复杂的局部散射包围，从而导致较为严重的信道衰落；（3）为实现远距离可靠传输，通信频段多集中在短波和超短波频段。

战术场景下信道传输特性的研究对提高军事通信的质量具有重要意义。传统的信道测量与建模研究中，通常假设信道满足广义平稳（wide-sense sta⁃tionary，WSS）非相关散射（uncorrelated scattering，US）。而TacMAN 场景下，发射机、接收机以及传播环境中的部分反、散射体都可能具有移动性，且发射端和接收端多采用高度相对较低的全向天线，传播环境快速变化，WSSUS假设不再适用，信道特性呈现时变非平稳特性［1］。现有的标准信道模型多为蜂窝信道模型，无法反映TacMAN场景下信道的时变非平稳特性，因此有必要展开针对性的测量建模研究。

反映实际环境影响和真实无线电传播行为的无线信道模型，对战术自组网的构建有着极为重要的影响［2］。目前国内外已有诸多学者和机构针对军事通信场景下的信道测量与建模进行研究。美国陆军工程研究与发展中心对军用低UHF 频段山区与城市场景点对点通信非视距信道进行详细测量，并开发一种地理空间模型用以预测城市信道［3-5］。文献［6］针对日本消防、公安机关通信系统常用频段即VHF 频段190 MHz 频点展开信道传播实验，对接收信号的功率、时延分布和衰落特性展开分析。文献［7］使用抽头延迟线方法，并基于ITU-R M.1225 模型，对战术自组织网络的小尺度特性进行建模。为研究军用UHF 频段下城市环境点对点传播特性，文献［8］就室内固定收发和室内固定发送、室外移动接收两种场景展开信道测量，并给出了功率时延谱（power delay profile，PDP）、衰减率和时延色散特性。这些已有的TacMAN相关场景下的信道模型仍以平稳信道统计性建模为主，缺乏对非平稳特性的探讨。参考MANET 场景下信道探测和建模的已有成果，在对车对车复杂通信网络中，信道可能因为周围散射体的快速变化，呈现明显的非平稳特性，例如文献［9］针对车对车网络复杂场景展开信道测量，并对动态信道进行建模与仿真，对其非平稳特性进行分析。然而，区别于普通MANET，TacMAN使用的军用VHF 频段通常具有更低的链路速率和更长的传播范围，例如美军新一代陆军手持电台Har⁃ris AN/PRC-163 在R/T1 下使用频率范围包含VHF 118～174 MHz，信道带宽包含例如5 kHz、1 MHz 等。因此，MANET 与TacMAN 场景下电磁传播特性存在显著区别，针对普通MANET 的研究不太适用于战术环境［10］，相关数据和模型也无法直接应用于Tac⁃MAN场景。

本文以城市战场环境为背景，模拟TacMAN 场景，展开信道外场测量，基于测量数据提取信道多径结构的动态变化，实现TacMAN非平稳信道建模。首先设计信道测量方案，获取相应场景下信道实测数据，进行数据处理；随后提出非平稳信道建模方法，通过对多径信号的识别与跟踪，获取多径信号生灭模型，并建立基于马尔可夫链的改进型非平稳TDL 模型；最后给出非平稳信道建模结果，对模型参数进行特征提取和分析，包括多径存在概率、时延和幅度分布，并使用所建立的信道模型与测量数据进行比较验证，证实了构建模型的准确性。

2 信道测量

2.1 测量方案

本实验测量系统示意图如图1所示。测量频段选择TacMAN 通信常用的超短波150 MHz。在邻近频段均被密集占用的情况下，为限制干扰，将探测序列的码片速率限制在1 Mcps［11］。发送端由矢量信号发生器NI 5673E循环发送中心频率为150 MHz、帧长为4096的伪随机序列恒包络零自相关（Constant Am⁃plitude Zero Auto-Correlation，CAZAC）序列，接收端经低噪放大器，由矢量信号分析仪NI 5663E 采集接收数据。为提高多径分辨率，接收端以5倍速率进行过采样。多径时延分辨率经过采样后达到0.2 μs，多径距离分辨率为60 m。收发两端均采用柱状全向天线，并配备GPS接收机用于提供同步与定位信息。测量系统更多细节及其余前期工作参考文献［11-12］。

本次测量地点为位于中国南方某地城区，发射端天线固定于一运输车顶部，距离地面高度约5.5 m。如图2所示，接收端天线搭载于测量实验车辆顶部，距离地面约2 m，车速约为30～50 km/h。在城区典型场景设计多个环形测量行驶路线，共在93个测量点获得约23000 个有效的信道冲激响应（channel impulse response，CIR）。

2.2 测量数据处理

本文基于滑动相关法开展宽带信道探测。接收端对接收数据与本地序列进行相关处理，从而获得CIR 快照。此时滑动相关输出信号含有CIR 信息，但也包含大量噪声，难以直接获取可分辨多径信号及参数，需要进行去噪处理。采用基于恒虚警率的噪声门限法［11］，假设噪声幅度服从Rayleigh 分布，根据Rayleigh 分布的概率密度函数和噪声中位值估计噪声标准差，从而设置噪声门限。低于该门限时，认为所测得的脉冲均由噪声引起，进而动态滤除每个快照中的噪声成分，保留有效多径分量。利用空间交替广义期望最大化（space-alternating general⁃ized expectation-maximization，SAGE）算法，从经过滤噪处理后的CIR 中提取多径信道参数，包括多径时延、多径功率信息。

3 TacMAN非平稳信道建模方法

由于战场环境的不可预测性，如部队的迅速推进或撤离，都可能导致传输环境的快速变化和通信节点的快速移动。由此产生的反散射体随机出现或消失的现象，可能会导致反散射路径突然消失或出现，最终使得信道呈现多径信号生灭交替的时变非平稳现象，需对TacMAN信道建立非平稳模型。

本章探讨TacMAN 下非平稳信道建模方法。首先介绍非平稳信道模型，包括CIR表达式及模型参数构成。其次，基于实测数据，提出一种多径识别与跟踪算法，基于马尔可夫链构建多径信号生灭模型。最后，根据多径识别与跟踪结果，获得建立非平稳信道模型所需要的模型参数，包括多径存在概率、多径时延和幅度分布。非平稳信道建模流程如图3所示。

3.1 非平稳信道模型

本文采用改进的非平稳TDL 模型来表征Tac⁃MAN场景下的单输入单输出（Single Input Single Out⁃put，SISO）无线信道，表征多径信号的动态演进过程。与传统的TDL 模型相比，多径信号的生灭状态作为一项新增的开关系数，被考虑到改进的信道冲激响应的表达中，基于多径生灭概率来控制每一条径的状态［1］。其信道冲激响应表达式如下：

其中al(t)、φl(t)和τl(t)分别表示t时刻第l条径的幅度、相位和时延，L(t)表示t时刻多径数量。新增的开关系数zl(t)表示t时刻第l条径的生灭状态。z=0表示开关打开，多径处于灭状态，z=1 表示开关闭合，多径处于生状态。模型示意图如图4所示。

3.2 多径识别与跟踪

基于2.2 小节处理后的测量数据，通过设置低于每一测量点处的主径功率的25 dB 为阈值［13］，将相应测量点处强度高于该阈值的多径信号视为处于“生”状态，低于该阈值的视为“灭”状态，滤除处于灭状态的多径分量。最终得到的实测信道多径信号在时延-时间平面的分布如图5 所示，测量期间多径信号时延随时间变化呈现较为杂乱的变化规律。为捕捉多径信号在时间尺度上的动态变化，基于多径分量距离（Multi-path Component Distance，MCD）提出一种时延域多径信号识别与跟踪算法。

MCD 最早在文献［14］中被提出，用以量化多参数域中多径间的距离，度量了多径间的相似性，如文献［15］基于MCD提出一种自动分簇和跟踪算法。本实验中信号带宽受限，多径数量并不丰富，对此提出一种“多径质心”的迭代更新计算方法，通过MCD 度量多径信号与多径质心间的相似性，实现多径信号识别与跟踪。

为避免混淆，首先定义下文“多径信号”与“多径质心”。“多径信号”指观测区间内由实测数据提取得到的、具有各自额外时延的若干多径分量；“多径质心”指多径的时延域质心，首个区间的多径质心时延初始值由该区间多径信号的时延直接赋值，后续区间的多径质心时延为当前区间相应多径信号时延与上一区间相应多径质心时延的加权和。因此多径质心能够动态反映区间内多径的时延在时域的变化，可以辅助识别下一区间的多径信号。

假设k-1和k为两个连续的观测区间，C为多径质心的集合，Q为多径信号的集合。假设在第k-1区间已得到M个经上一区间更新得到的多径质心，包含各自的时延τ、功率P和编号ID：

在第k区间，通过TDL 模型得到N个多径信号，包含各自的时延和功率：

计算第k区间的第i个多径信号与第k-1 区间的M个多径质心之间的时延域MCD，对该多径信号与各个多径质心之间的相似性进行评估。MCDτ表达式如下：

其中τstd为区间k、k-1 内所有多径时延的标准差，。MCDτ越小，则多径间的相似度越高。设置门限ε，当MCDτ≤ε时，可认为多径符合相似度要求。

假设该多径信号与第j个多径质心最相似，即

则该多径信号及多径质心之间存在以下两种情况：

①若MCDτ，ij≤ε，则可认为该多径信号与第j个多径质心足够相似，即第k区间内的该多径是由第k-1 或其之前区间相应多径延续得到，该多径信号继承第j个多径质心的ID。第k区间的该多径质心需进行更新，更新后的时延由相应多径信号和多径质心各自的时延根据功率加权得到，以避免低功率的多径分量与高功率的多径分量产生相近的影响。表达式如下：

其中系数μ为第k-1 区间多径质心的影响因子，用于在必要时赋予其更多的比重。本实验中该值取值为9。

②若MCDτ，ij>ε，则该多径信号不属于任一多径，可以认为一条新径出现，该多径信号即为新的多径质心的初始状态。

对第k区间的全部N个多径信号完成上述步骤，则完成了第k个区间的多径识别与跟踪，且得到动态更新后的V个多径质心的集合Ck：

对全部区间重复上述行为，最终实现全部观测区间内多径信号的识别与跟踪。假设最后一个区间的多径质心数量为Vmax，则表示该算法经识别和跟踪后得到的多径种类的数量为Vmax。

在上述过程中，门限ε的取值极大程度上决定了识别与跟踪的准确性。经相关性计算，各区间内多径信号与其对应多径质心之间的时延误差的总和与门限ε之间的线性相关系数为0.87，成正相关，即降低ε的值将减小时延误差。而算法最终分辨得到的多径种类的数量Vmax与门限ε之间的线性相关系数为-0.89，为负相关，即降低ε的值将提高多径区分能力，使得识别到的多径种类的数量增加。为实现较小的时延误差和合理的多径种类数量之间的平衡，通过初步仿真和数据分析，选取ε=0.032作为本实验的门限。

3.3 马尔可夫生灭模型

根据上一节得到的多径识别与跟踪结果，对多径信号的生灭过程进行建模。采用简单的一阶二状态马尔可夫链描述多径生灭状态的持续和跳转。如图6 所示，其中“0”表示多径信号消失即“灭”状态；“1”表示多径信号出现即“生”状态。

马尔可夫链可由状态转移矩阵和稳态向量描述，表达式分别如下：

其中条件概率Puv=Pr{Sn+1=v|Sn=u}，表示多径信号的生灭状态由u跳转到v的概率；S0、S1分别表示当系统进入稳态后，生、灭状态各自的稳态概率。式（1）中多径的存在概率zl(t)由稳态向量得到，即Pr{zl=0}=S0表示多径消失概率，Pr{zl=1}=S1表示多径存在概率。

3.4 小尺度衰落建模方法

在对多径小尺度衰落幅度分布建模时，使用AIC 准则选取最优拟合分布。AIC 表示候选分布与实测样本间的近似无偏估计量，AIC 越小表明拟合越佳。第j个候选分布的AIC由下式给出［16］：

其中N为样本x的数量，为分布参数的最大似然估计，表示该参数下该候选分布的概率密度函数，U表示该分布的维度。为便于比较各候选分布的拟合效果，引入AIC偏差［16］：

4 TacMAN非平稳信道建模结果

为描述上述非平稳模型，需对模型参数进行提取，包括存在概率、多径时延和多径幅度分布。

4.1 多径时延与存在概率

根据3.2节所述方法对城区测量数据完成的多径识别与跟踪结果如图7 所示，对93 个观测样本的约23000 个有效CIR 进行处理，各区间内根据TDL模型提取得到的多径由图中散点表示。共识别得到6 条多径，以不同线型区分多径种类。其中灰色实线表示多径质心的跟踪结果，显示了其在时间域上的动态演进过程。可以发现部分径十分密集，在整个观测时间内都存在，而另一些径较为稀疏，出现了明显的生灭现象。

为体现多径时延为在所有测量区间累计影响下的最终结果，由多径质心在最后一个测量区间的时延描述相应多径时延，如下文表3所示。

采用一阶二状态马尔可夫链对上述6条径的生灭过程进行建模，以第6径为例，当多径出现时标记为1，消失即低于主径25 dB时标记为0，其状态转移矩阵TS6=[0.81 0.19；0.75 0.25]，稳态向量为SS6=[0.79 0.21]。

6 条多径的马尔可夫模型参数如表1 所示。从整体上看，随着时延的增加，多径的存在概率S1总体呈下降趋势，多径保持灭状态和由保持生状态的概率P00、P11分别呈上升和下降趋势，说明多径时延越大多径越不稳定的规律。

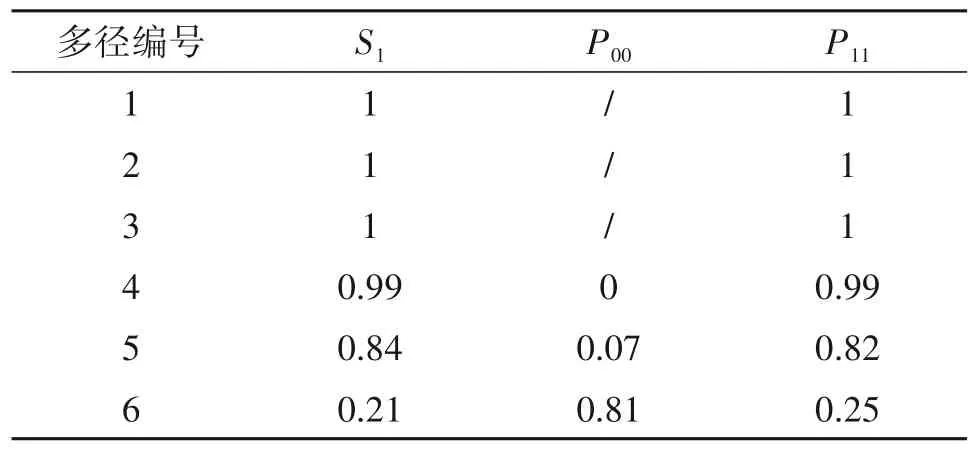
表1 马尔可夫模型参数Tab.1 Markov model parameters

4.2 幅度分布

最初采用常用的Rayleigh、Ricean、Nakagami 和Weibull分布作为小尺度衰落幅度分布的候选分布。四者的概率密度函数如下：

其中I0(·)和Γ(·)分别表示零阶贝塞尔函数和Gamma函数。

处理时发现第1 径的幅度分布呈现出特殊现象，如图8中直方图所示，信道幅度的一部分集中在小值区，另一部分集中在拖尾区。如图8（a）所示，这种特定的幅度分布使得常见的Rayleigh、Ricean、Nakagami 和Weibull 分布均难以实现良好的拟合。这里由于65%的样本分布在零值附近，使得LOS 分量的估计功率为0，导致Rayleigh 和Ricean 的拟合曲线彼此吻合。较大的拟合误差最终将会导致建模结果失真。为此，引入自由度更高的BGMD 作为候选分布之一。BGMD概率密度函数如下：

其中ω为混合系数。BGMD 拟合效果如图8（b）所示，可以直观地看出BGMD 对较小幅度处的峰值及较大幅度处的拖尾均能实现较好的拟合效果。

表2、表3 分别显示了各条径在各候选分布下的AIC权重估计值及相应最优分布的拟合参数。可以看出，BGMD最适合第1径。第1径幅度分布为两个高斯分量的混合，其中弱分量权重为0.65，均值为0.02，方差为0.01，强分量均值为0.23，方差为0.12。认为弱高斯分量为在最强径即第2径之前到达接收端的来自NLOS 区的散射和反射路径，这是由于测量环境包含作为散射体和障碍物的大面积大型建筑物。而权重较小的强高斯分量可能来自于被植被覆盖的零星LOS 区。该地区的收发路径存在灌木丛、围栏和其他轻微障碍物。由于发射端和接收端天线高度仅为5.5 m 和2 m，LOS 分量的概率相应降低。因此，BGMD 适用于描述复杂城市TacMAN场景中第1径的统计分布。

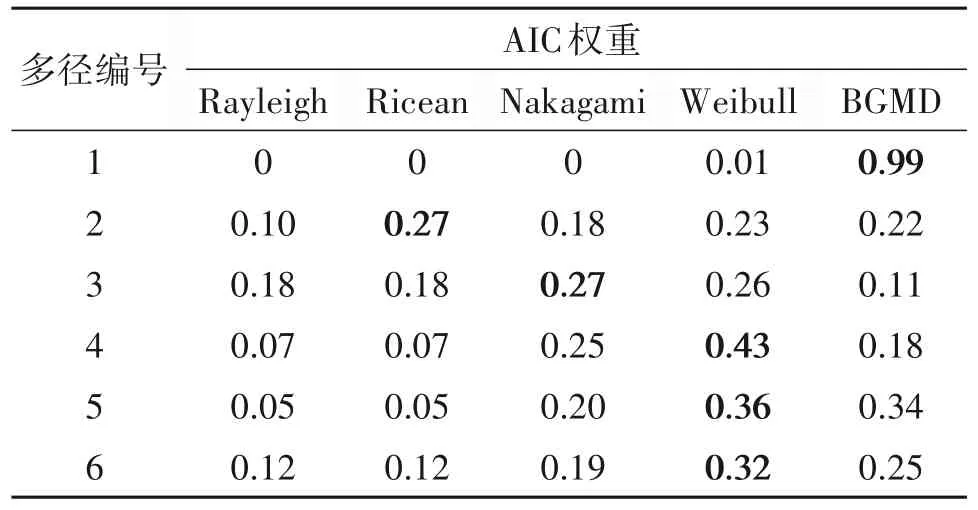
表2 候选分布AIC权重Tab.2 AIC weights of the candidate distributions

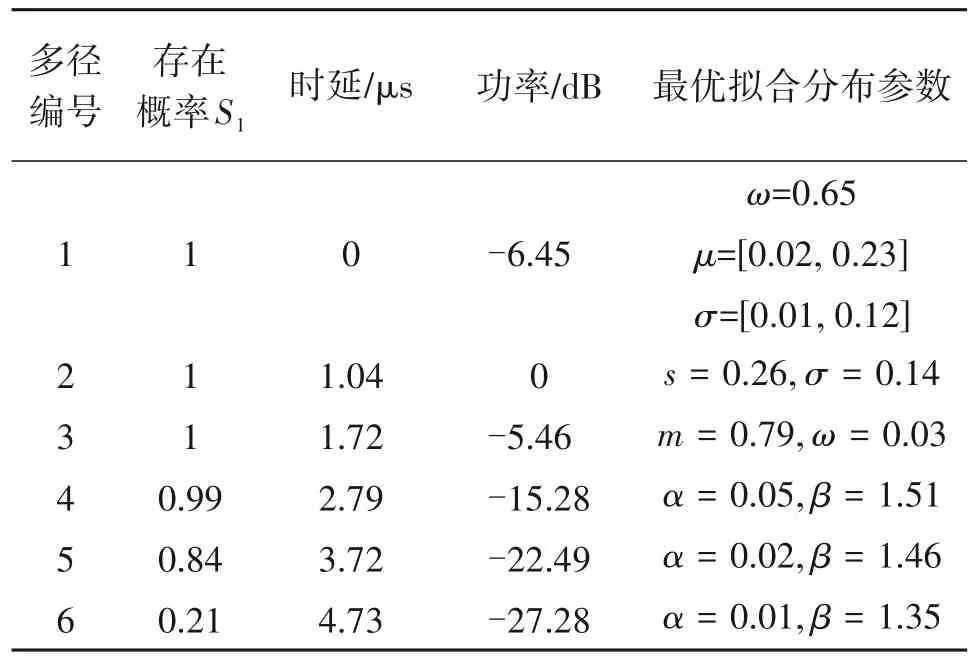
表3 测量城区MANET信道TDL模型Tab.3 The TDL model of measured urban MANET channel

此外，本次测量数据中第2径为最强径，其幅度分布如图9所示。该径由Ricean分布实现优势不显著的最优拟合，且主信号幅度峰值为0.26，认为测量环境中存在一定概率的LOS传播。除第2径外，其余各径Rayleigh 分布与Ricean 分布AIC 权重值近似相等，此时Ricean 分布主信号幅度峰值近似为0，接近Rayleigh 分布，说明由于城区测量场景环境复杂，通信覆盖范围较大，反散射体随机分布，LOS传播阻碍严重。Weibull分布对大部分径实现最优拟合，证明Weibull分布良好的灵活性，且Weibull形状参数β均小于2，说明本测量场景下信道衰落普遍严重。

4.3 模型验证

表3给出了由上述建模方法及数据及数据分析得到的非平稳信道建模结果，包括多径存在概率S1、多径时延及幅度分布。

根据表3 中给出的信道模型及多径参数，对所测非平稳信道模型进行仿真验证。采用式（1）所示的CIR表达式，根据公式（5）、（6）获得的多径稳态向量SS、状态转移概率TS，随机生成仿真多径信号在时域维度的生灭状态z(t)。根据表3 给出的多径时延与AIC 准则下最优幅度分布及参数，生成仿真多径信号的时延和幅度信息。最终得到的多径结构仿真结果如图10 中深色脉冲所示。浅色部分为实测信道冲激响应。图中定性且直观地显示了仿真数据能够较好地反映实测数据的特性，说明了本文所提取的信道参数和特性具有良好的准确性。

此外，使用均方根时延扩展（Root-Mean-Square Delay Spread，RMS-DS）对模型统计特性进行进一步验证。RMS-DS 为PDP 二阶矩平方根。根据式（1），其表达式为：

其中，平均时延μτ=。

图11 为实测数据与仿真数据下RMS-DS 的累积分布函数（Cumulative Distribution Function，CDF）曲线。仿真曲线对实测曲线的吻合程度进一步证明了本文所建立的非平稳信道模型能够较好地描述实测环境下通信信道的传输特性。

5 结论

本文基于城市战场环境下超短波频段测量数据，研究模拟TacMAN通信信道的非平稳特性，建立包含多径生灭信息的统计非平稳信道模型。分析和建模结果表明，TacMAN 场景下多径信号存在不可忽视的非平稳生灭现象，且多径时延越大，存在概率越低，多径信号越不稳定。城区复杂TacMAN通信中，当信道首径由强路径分量和弱路径分量组成时，BGMD 呈现出对该径幅度分布的拟合优势。最强径以Ricean 为最优分布。其余各径大都以形状参数小于2的Weibull分布实现最优拟合，说明本次测量环境下信道衰落普遍严重。与传统的平稳信道模型相比，本文建立的非平稳信道模型提供了更细致的信道描述，为TacMAN 场景下的信道研究提供了建模方法，并为相关军事通信系统的设计与优化提供参考。未来的工作包括对TacMAN电磁环境特性进行更深入的挖掘和建模等。