基于核心素养的数学命题策略初探

文／陈雪云

引 言

考试是检验学生学习效果的有效方式之一。在小学数学教学中，教师对试题进行合理命制，能够及时了解学生的学习情况。在核心素养背景下，教师要改变命题方式，让试题更贴近学生的生活，通过试题帮助学生巩固知识，培养学生数学学科核心素养。基于以上思考，笔者在小学数学试卷命题的实践中做了以下几点尝试。

一、联系生活，设计能够培养数学抽象能力的题目

数学命题必须取材于学生的现实生活，即在不改变数学本质的前提下，将命题融入学生的生活实际，把纯粹的“解数学题”变成日常的社会活动，让学生在活动中运用所学的数学知识解决实际问题或解释生活现象，同时让解题本身成为一种学习过程，在这一过程中挖掘学生的学习潜能[1]。

例题：晶晶和同学约好一起去金马影院看电影（电影播放信息如图1），电影院提前5 分钟停止检票，晶晶和同学必须在下午（ ）前去检票。如果他们看完电影马上回家，途中共需要15 分钟，他们可以在（ ）到家。

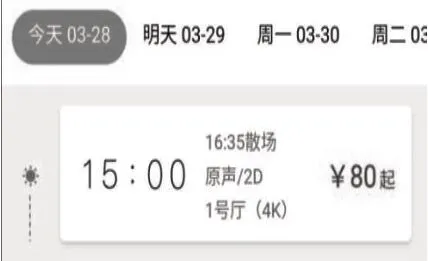
图1

A.14:55 B.2:55 C.16:50 D.4:50

这道题打破传统的命题模式，把对24 小时计时法和求简单经过时间的知识点考查融入学生熟悉的看电影的活动，取材于学生的现实生活。电影票上的信息丰富，学生必须根据实际的需要，选择有效的信息来解决问题。这是对学生提取信息并进行分析推理的能力及认真审题良好习惯的全面考验。在解决问题的过程中，学生运用了年、月、日的相关知识，解决了看电影中的数学问题，深刻地体会到数学与生活的紧密联系，产生了“数学有用”的情感体验，并学会将生活中的数学现象抽象成数学问题并用相关知识加以解决，培养了数学抽象能力。

二、设计“非常规问题”，培养数学推理能力

核心素养导向下的数学命题应尽量避免考查对具体知识的记忆和模仿，应侧重对能力的测试和培养。命题时，教师应关注学生的“最近发展区”，设计一些“非常规”问题，但要保证学生可以基于以往积累的数学活动经验和知识储备综合处理新问题，发展数学推理能力和综合运用知识解决问题的能力。

例题：图2是用6 个边长为1 厘米的小正方形拼成的，那么这个图形的周长是（ ），面积是（ ）。

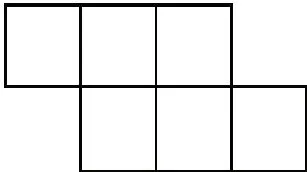
图2

A.24 厘米，24 平方厘米

B.12 厘米，6 平方厘米

C.20 厘米，8 平方厘米

D.12 厘米，8 平方厘米

周长和面积的知识是小学数学空间与图形领域的核心知识，这题考查学生能否掌握周长和面积的定义，而不是让学生按照周长与面积的计算公式直接求出周长和面积。学生要解决这道题必须知道什么是图形的周长和面积，以及怎样去计算一个不规则图形的周长和面积，也就是理清周长和面积这两个概念之间的区别，运用转化等策略顺利解决问题。这样的命题避免了学生直接套用公式和机械模仿，考核学生的高阶思维能力、数学推理能力和综合运用知识解决问题的能力，能促进学生核心素养的发展。

三、关注个性差异，设计培养数学建模能力的问题

学生作为独立的个体，存在鲜明的个性差异。《义务教育数学课程标准（2022年版）》指出，评价要充分关注学生的个性差异。这就要求教师在命题时设计一些灵活开放且富有弹性的题目，让不同层次的学生可以根据自己的需要选择问题。这既能保护学困生的自尊心和学好数学的信心，又能激发学优生积极挑战自我的热情，使所有学生都能得到发展。

例如，在教学完“解决问题的策略——从问题出发”后，笔者设计了试题：“请根据图3中的信息，自己提一个问题，并解答”。

图3

这道题目的信息量非常丰富，问题的要求也颇有层次性和开放性。学生可以根据自己的需要提出问题，既可以提一步计算的问题，也可以提两步或多步解答的问题，再根据问题的需要，选择两个或多个相关联的条件进行解答，充分发挥求异思维，培养学生的创新意识和问题意识。在此过程中，学生能够主动建构“从问题出发→找相关联条件→分析解答”的解决问题策略的数学模型，提高数学建模能力。

又如，在苏教版四年级（上册）“统计与可能性”单元中，结合学生熟悉的永辉超市“双12”抽奖促销活动，笔者设计了“我会策划”题目：“新永辉超市的电器部想要设计一个有创意的抽奖方案，你能按照获奖要求（如图4），帮商家设计规则吗？”

图4

在这道题中，学生可以充分将可能性的有关知识应用于生活，既可以根据自己的兴趣选择不同的材料（如骰子、转盘等）进行设计，也可以根据自己的能力水平进行难易不同的规则设计。这样的题目设计既关注差异性，又充分激发了学生的创造性，培养了学生的创新意识和创新能力。

四、关注学习过程，设计促进数学思考的问题

比知识本身更重要的是以知识为载体的基本数学思想和思维能力及数学活动经验。拥有这些数学素养和能力才能在学习中做到触类旁通、举一反三[2]。因此，在数学命题过程中，教师要重视对学生学习过程的考查，使命题再现知识的形成过程和思维过程，促进学生进行数学思考，使命题起到反馈教学、诊断教学、促进教学的作用，使学生在解决问题的过程中提升数学能力，发展核心素养。

例如，在学生学完两位数乘一位数的乘法后，笔者尝试设计了题图5和图6。

图5

图6

如果教师让学生列竖式计算52×15 或16×4，通过模仿、记忆和强化训练，绝大部分学生能够掌握算法，但对其中的算理却一知半解，似懂非懂。这种“重算法，轻算理”的考核，忽略了知识形成的过程，限制了学生思维能力的发展。图5联系实际情境考查学生对算式意义的理解，而图6用数形结合的方式，巧用小棒图，通过多元辩证的方法，让学生通过直观加动作的表征转化为符号的表征，理清进位“2”的含义。这两题都从算法→意义→算理三个层次考查学生对两位数乘法的掌握程度，让学生通过答题充分展示自己的思维过程。教师可以将学生的典型答案进行归因、分析，及时调整教学策略，帮助学生在理清算理的基础上进一步巩固算法，做到“知其然，知其所以然”，培养学生几何直观能力和数形结合的数学思想。

五、留有探索的空间，设计能够培养学生探究意识和探究能力的问题

在命题时，教师应对知识进行整合，在知识的交汇处命题，留给学生一定的探索空间，培养学生探究意识、探究能力和综合运用知识解决问题的能力。

例如，在教学三年级（下册）“混合运算”单元后，笔者设计了以下题目。

把1 厘米的小棒按下面的规律拼一拼（如图7），你知道第9 个图形需要多少根小棒吗？第99 个呢？可以用拼一拼，也可以用画图、计算或列表比较等方法做出解释，最后完成表1。

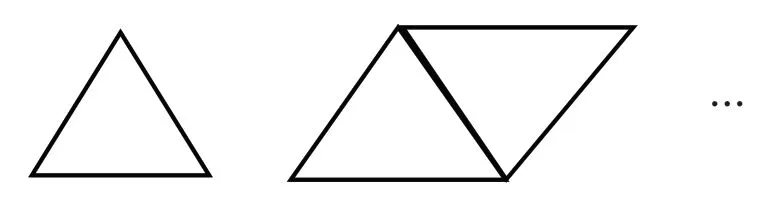
图7

表1

这道题让学生自由选择直观操作、计算、画图或列表比较的方式建构答案，探索拼三角形所需小棒数量变化的规律，可以让学生感受混合运算的广泛应用价值。命题既要关注对数学问题进行数学抽象，也要关注对数学模型的自主建构，更要关注对数学模型的实际运用，从多角度考查学生的思维品质，做到过程与结果并重，知识再现与探索发现并行，引领学生去探索、发现、经历知识形成的全过程，培养学生的探究意识和探究能力。

又如，在教学苏教版“平行与垂直”单元时，笔者设计了下题。

（1）比较图8中∠1和∠2的度数，你有什么发现？

图8

（2）在两张长方形纸的宽重叠后，继续绕A 点旋转（如图9），从图a 到图n 的变化过程中，你能发现∠1 和∠2 的度数有什么关系吗？

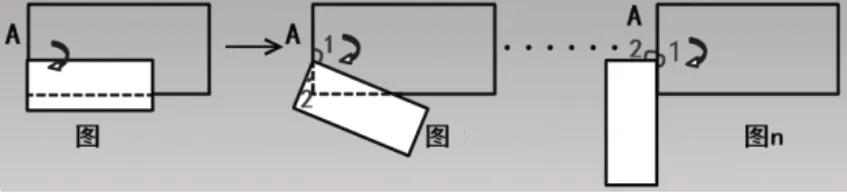
图9

本题通过图引导学生探究：在一个长方形绕中心点运动过程中，∠1 和∠2 的度数之间存在的关系。在解题中，学生经历了观察想象、举例验证、发现规律、应用规律的探究过程，发现了在图形运动过程中变与不变的关系，自主建构“一个平角中减去一个直角，剩下两个角的和一定等于90 度”这个规律，以及探究规律的一般方法。第（2）小题继续探究当上一个图形旋转到下一个图形之外时，∠1 和∠2 度数之间的关系。此题化静为动，凸显知识本质，留给学生充分的探索空间，能够培养学生的探究意识，发展学生的空间想象、分析、推理和综合运用知识解决问题的能力。

课堂的时间和空间是有限的，但学生思维的空间却是无限的，只有激发学生的探究意识，培养探究的能力，才能为他们的思维插上翅膀，让学习走向远方。

结 语

总之，核心素养评价下的数学命题要把知识、能力、态度整合，做到知识与过程并重，能力与发展并行，情感、态度、价值观共举。在此基础上，教师要通过考试评价，引导学生在掌握“四基”的基础上，学会数学抽象、数学推理和数学建模，提升核心素养，促进教、学、评一体化。