基于DDPG算法的可再生能源系统竞标策略

冯伊豪，黄 超，王 龙，罗 熊

(1.北京科技大学 计算机与通信工程学院，北京 100083;2.北京科技大学 顺德研究生院，广东 佛山 528399)

0 引 言

近年来，中国可再生能源发展迅速。截至2020年底，全国风电装机容量达2.81亿千瓦、光伏装机容量达2.53亿千瓦，占全部电力装机的24.3%[1]。受气候等环境因素的影响，可再生能源出力具有很大的不确定性，弃风、弃光问题严重，这给电力现货市场带来了巨大的挑战[2]。随着可再生能源装机容量的快速增长和电力现货市场建设步伐的不断加快，可再生能源参与电力市场竞标策略研究对提升电厂的经济效益愈发重要[3-4]。如何对可再生能源出力与电价的不确定性进行适当建模和求解是值得研究的重要问题。

可再生能源参与电力市场竞标优化建模大多基于可再生能源发电功率概率分布模型来应对功率的不确定性。Pinson等[5]在风力发电概率预测方法的基础上，提出了一种风力发电项目竞标的通用方法。基于随机规划[6]、鲁棒优化[7]、机会约束规划[8]的不确定性规划模型常用于电力市场竞标优化建模。与随机规划模型和鲁棒优化模型相比，机会约束规划模型的显著特点是可方便建立风险可控的优化模型。可再生能源系统还可以通过储能系统、电动汽车等设施增加系统的灵活性，减少可再生能源的不确定性对竞标策略的影响。

深度强化学习(Deep Reinforcement Learning，DRL)采用深度神经网络进行特征提取和函数逼近，已在游戏、机器人控制、参数优化、机器视觉等领域得到了广泛的应用[9]。可再生能源的竞标和调度优化这类时序控制问题也可用强化学习进行求解。

Rahimiyan等[10]引入Q-learning[11]算法解决传统发电公司的投标决策问题。Boukas等[12]将日内市场交易的顺序决策问题建模为马尔可夫决策过程，提出一种基于深度Q网络[13](Deep Q Network，DQN)算法的解决方法。Cao等[14]提出利用异步的优势行动者评论家[15](Asynchronous Advantage Actor-Critic，A3C)算法为风力发电商制定现货电力市场和储备市场的智能竞标策略，以对冲由于风能调控价格的不确定性造成的利润损失风险。

刘国静等[16]通过引入Q-learning算法解决了如何将不确定性的风电与储能系统有机结合、提高效能的问题。刘俊峰等[17]提出利用DQN算法对基于能源总线模型的微能源网进行能量管理与优化策略研究。张自东等[18]构造了包含蓄电池和储氢装置的微电网复合储能模型，采用DQN算法对微电网系统的能量调度进行决策优化。

该文以最大化风-光-储可再生能源系统的经济效益为目标，提出了一种基于深度确定性策略梯度(DDPG)算法的日前电力市场竞标和日内实时能量调度结合的方法，利用神经网络从历史数据中学习制定竞标策略和调度策略。可再生能源参与电力现货市场竞标的难点在于如何应对发电功率与电价的不确定性。预测是解决这一难点的常用方法。但电价受电厂发电量、用电行为、厂商竞标策略等影响，日前预测精度不高。与传统日前竞标策略不同，该文建立的基于DDPG的日前竞标策略无需日前电价预测信息。面向日内实时平衡市场，该文利用SARIMA模型对不平衡电价进行超短期预测以制定基于DDPG的日内能量调度策略。为验证算法的有效性，基于实际数据开展算例研究，实验结果表明提出的基于DDPG算法的日前竞标策略与实时能量调度策略可较大程度地提升系统的经济效益。

1 可再生能源系统电力现货市场竞标优化模型

1.1 风-光-储可再生能源系统

风-光-储可再生能源系统由风力发电、光伏发电以及蓄电池储能系统三个模块构成，其结构如图1所示。其中，风力发电模块和光伏发电模块将风能和太阳能转换为电能供给公共电网或储能系统。

图1 风-光-储可再生能源系统结构

蓄电池储能提升了可再生能源系统的灵活性。一方面，蓄电池储能系统可通过在低电时价储能高电时价放电提高系统收入。另一方面，可通过调节储能系统的充放电减少实际发电量和竞标电量的偏差，帮助系统克服可再生能源发电功率和电价的不确定性对竞标策略的影响。

1.2 蓄电池储能系统

储能系统的能量状态满足公式(1)：

EB,t+1=EB,t+PB,tΔt

(1)

其中，EB,t和EB,t+1分别表示储能系统在t时段和t+1时段初始时刻的电量状态。PB,t表示t时段储能系统的充放电功率，PB,t>0表示储能系统充电，PB,t<0表示储能系统放电，PB,t=0表示储能系统闲置，既不充电也不放电。蓄电池储能系统满足以下运行约束条件。

(1)充放电功率需满足式(2)：

PB,min≤PB,t≤PB,max

(2)

其中，PB,max和PB,min分别为储能系统的最大、最小充/放电功率。

(2)储能系统电量需满足式(3)：

EB,min≤EB,t≤EB,max

(3)

其中，EB,max和EB,min分别为储能系统的最大、最小储量。

(3)一个交易日的始末电量需满足式(4)：

EB,open=EB,end

(4)

其中，EB,open和EB,end分别为一个交易日始/末时刻的储能系统储电量。

1.3 电力现货市场竞标优化模型

北欧现货市场[19]由日前市场、日内市场和实时平衡市场3个部分构成，其交易标的均为电能。日前市场和日内市场均由北欧电力交易所负责组织。日前市场于日前12：00闭市，在13：00向市场公布出清结果。日内市场是日前市场的补充，于日前14：30开始，持续滚动出清直到实时运行前一个小时。平衡市场由各国TSO(Transmission System Operator)分别组织，各国TSO将依据市场成员的调整报价信息，以再调度成本最低为原则对电网进行平衡调度，最终形成上调/下调边际价格。

该文只考虑北欧电力现货市场的日前市场和平衡市场，不参与日内市场，且可再生能源系统为价格接受者，其收益如下：

(5)

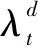
收益还可以写为：

(6)

其中：

(7)

(8)

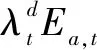
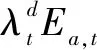
目标函数为：

(9)

即在满足蓄电池储能系统的约束条件下，求解{Ebid,t,ΔEB,t}使得可再生能源系统收益最大。如何处理可再生能源出力和电价的不确定性是求解该优化问题最大的难点。

2 基于DDPG算法的竞标策略

2.1 马尔可夫决策过程

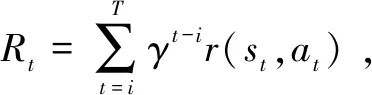
强化学习中使用值函数来评估策略π，分为状态值函数Vπ和动作值函数Qπ两种，其中，Vπ(s)表示在状态s由策略π得到的累计期望奖励，Qπ(s,a)表示状态动作对(s,a)由策略π得到的累计期望奖励。动作值函数如式(10)：

Qπ(s,a)=r(s,a)+

(10)

式(10)也被称为Bellman公式。强化学习是为了获得最大化累计奖赏的最优策略π*，对应的Q*(s,a)为：

Q*(s,a)=r(s,a)+

(11)

式(11)被称为最优Bellman公式。

2.2 深度确定性策略梯度算法

深度确定性策略梯度[20](Deep Deterministic Policy Gradient，DDPG)算法以行动者-评论家(Actor-Critic)框架为基础，同时结合了DQN算法以及确定性策略梯度[21](Deterministic Policy Gradient，DPG)算法的优点，可用于解决连续动作空间上的强化学习问题。DPG算法的策略梯度如式(12)所示：

(12)

DDPG算法在行动者部分引入确定策略梯度，利用式(12)更新策略网络参数，而在评论家部分利用式(13)对网络参数进行更新。

L(θQ)=E[(Q(st,at|θQ)-yt)2]

(13)

其中，

yt=r(st,at)+γQ(st+1,at+1|θQ)

(14)

为了减少网络震荡带来的问题，DDPG算法采用“soft”方式更新目标网络中的参数，可有效提升算法的稳定性，即创建新的评论家和行动者网络(Q'(s,a|θQ')和μ'(s|θμ'))，其更新规则为：

θμ'←αθμ+(1-α)θμ'

(15)

θQ'←αθQ+(1-α)θQ'

(16)

式(15)和(16)中，α远小于1。此外，DDPG算法通过引入经验回放机制打破样本的关联性，从而提高参数更新的有效性。

针对DPG算法缺少对环境的探索的缺点，DDPG算法通过添加随机噪声N，使动作的选择具有一定的随机性，以完成策略探索，公式如下：

(17)

2.3 储能系统惩罚函数设置

对于蓄电池储能系统运行约束条件(2)，可通过限制神经网络输出来解决。为了使储能系统满足其他约束，定义蓄电池储能系统惩罚函数：

(18)

(19)

(20)

2.4 日前竞标策略马尔可夫决策模型

可再生能源系统参与日前电力市场竞标需于日前12：00提交交易日各小时竞标电量，可概括为一个MDP过程。该文提出了日前竞标策略马尔可夫决策模型可基于可再生能源发电功率预测信息，以可再生能源系统收益最大化为目标制定日前市场竞标计划和日前储能系统调度计划。日前储能系统调度计划为交易日各小时储能系统的充放电计划，可于实时运行前进行修改，而日前市场竞标计划提交后日内不再更改。

日前电力市场竞标模型状态空间

其状态特征如表1所示。

表1 日前电力市场竞标模型状态描述

如式(21)所示,奖励函数的构造需要结合目标函数(9)和储能系统惩罚函数(18)。强化学习的目的是使奖励函数最大化，因此需要在惩罚函数前加上负号。经过一段时间的训练，惩罚函数值基本趋近于0，即储能系统在满足约束条件下正常工作。

(21)

其中，PW,t和PPV,t分别为t时段的实际风力发电功率和实际光伏发电功率。

一个回合的总奖励为：

(22)

2.5 实时能量调度马尔可夫决策模型

基于日前竞标策略马尔可夫决策模型，该文提出了实时能量调度马尔可夫决策模型，可根据日前竞标计划和超短期预测信息于储能系统实时运行前调整日前储能系统调度计划以提高可再生能源系统的收益。

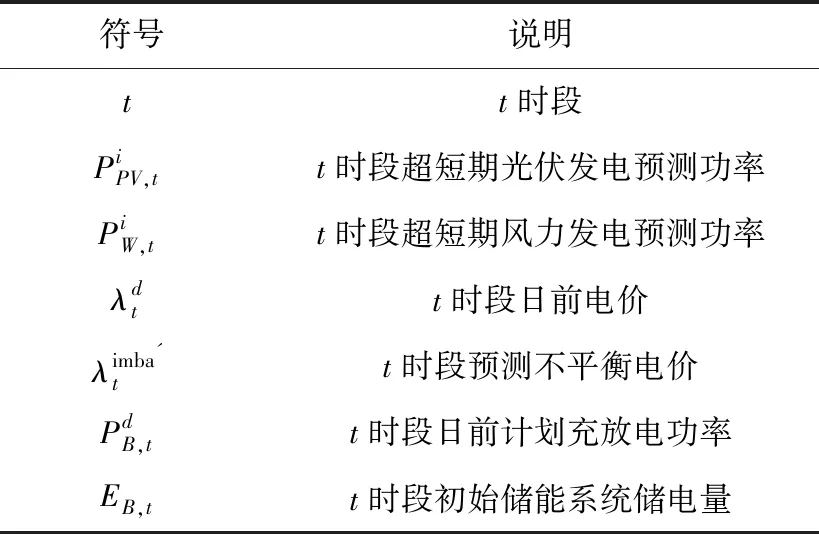
表2 实时能量调度模型状态描述

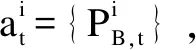
奖励函数如式(23)所示：

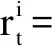
(23)

一个回合的总奖励为：

(24)

3 实验和性能

3.1 实验设置

该文模拟的可再生能源系统由风力发电装置、光伏发电装置和储能系统构成。风力发电装置、光伏发电装置标称功率均为100 MW，储能系统设置如表3所示。

表3 储能系统参数设置

风能数据和太阳能数据来源于Global Energy Forecasting Competition 2014(GEFCom2014)中一个澳大利亚风电场和光伏电场2012年4月1日至2013年11月29日的发电数据。电价数据来源于北欧电力市场(www.nordpoolspot.com)2018年4月1日至2019年11月29日日前电价和不平衡电价数据。风能数据、光能数据、电价数据均为608天，数据分为两组：前425天数据为训练集，用于训练模型；后183天数据为测试集，用于测试训练完成的模型的性能。测试集部分发电数据和电价数据如图2、图3所示。

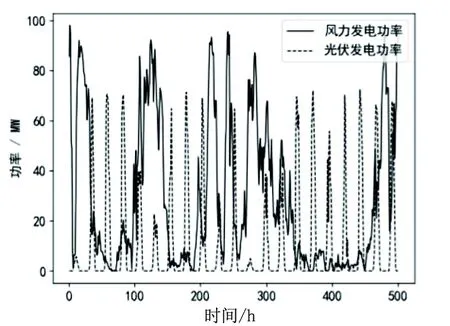
图2 测试集部分发电数据

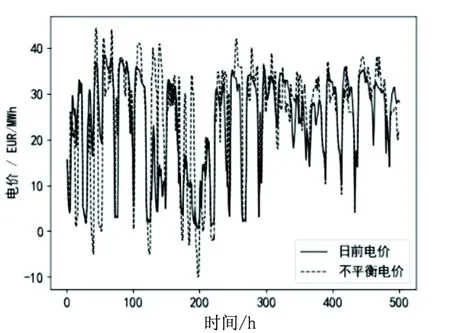
图3 测试集部分电价数据

通过向实际风电功率和光电功率引入高斯噪声的方式模拟风电预测功率和光伏预测功率。风机发电功率与光伏发电功率日前预测标准差均为10%，日内预测标准差均为5%[22]。采用SARIMA模型[23]对日内超短期不平衡电价进行预测，在测试数据上的平均绝对百分比误差为12.29%。

数据预处理模块对缺失值进行均值填充处理，并将风力发电功率与光伏发电功率归一化到0～1之间。由于电价数据波动幅度较大，对每日日前电价进行归一化处理，不平衡电价也做相应映射处理。

日前电力市场竞标DDPG模型的神经网络设置：行动者网络隐层两层，分别由200和100个神经元组成；评论家网络隐层两层，分别由200和150个神经元组成。日内实时能量调度DDPG模型的神经网络设置：行动者网络隐层两层，分别由200和100个神经元组成；评论家网络隐层两层，分别由300和200个神经元组成。实验的硬件环境为 Intel Core i5-7200 CPU，主频2.5 GHz，8 GB内存。软件环境为Windows 10操作系统，Python 3.7开发平台，tensorflow深度学习框架。超参数设置如表4所示。

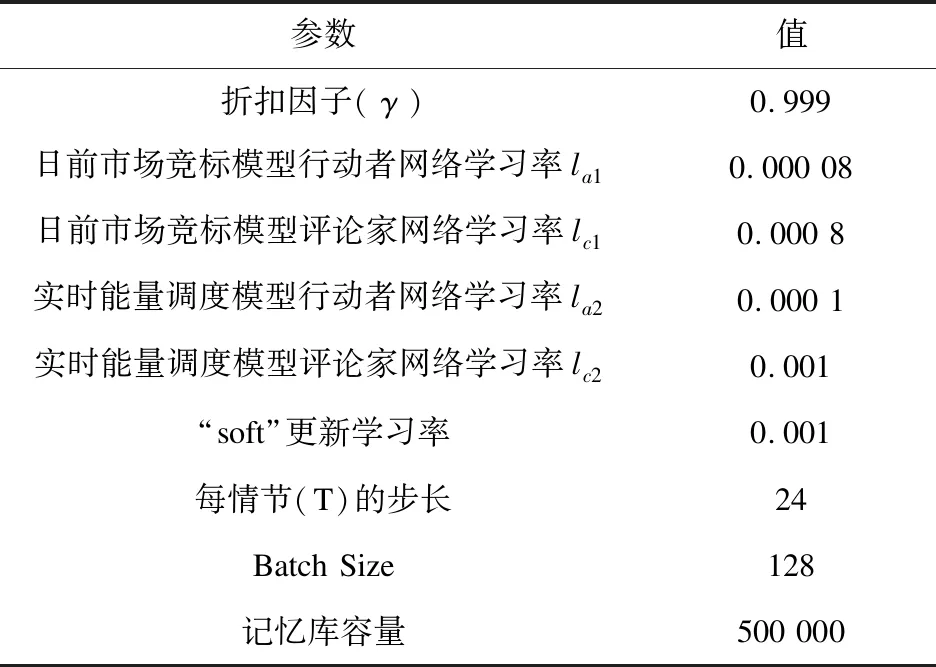
表4 DDPG模型超参数设置

3.2 实验结果

使用训练集进行训练时，先训练日前市场竞标DDPG模型，训练回合数为150 000，其奖励R1的变化如图4所示。基于日前竞标策略，训练日内实时调度DDPG模型，训练回合数为100 000，其奖励R2的变化如图5所示。

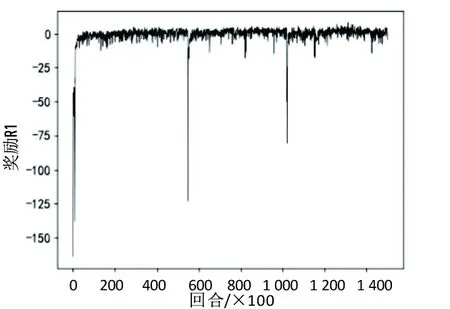
图4 日前市场竞标模型训练过程

图5 日内实时能量调度DDPG模型训练过程

为验证所提出的基于DDPG算法的模型的有效性，选取一个发电日进行案例分析，日前电价和不平衡电价如图6所示。

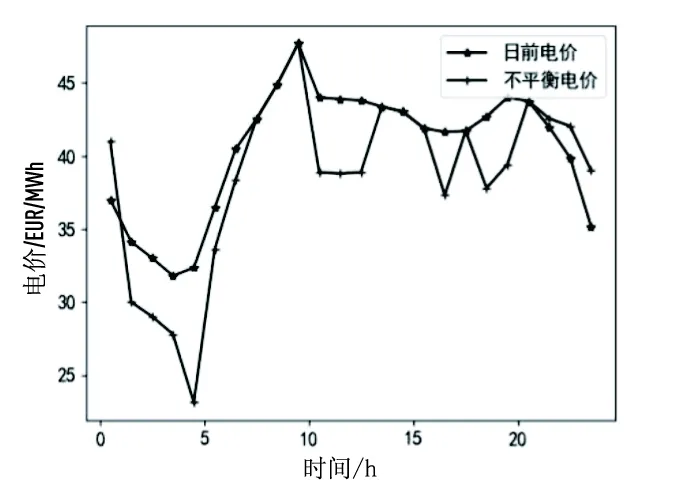
图6 某发电日电价

储能系统日前计划充放电功率和日内实际充放电功率如图7所示。可再生能源系统电能出力(风力发电和光伏发电)每小时日前短期预测值、日内超短期预测值、实际值和竞标电量如图8所示。

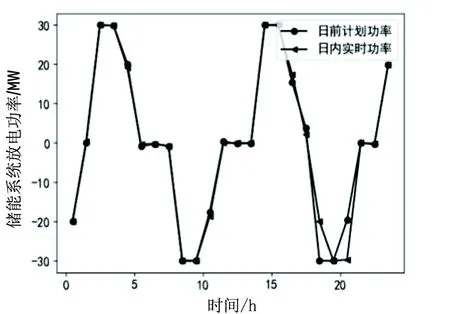
图7 储能系统日前计划功率与日内实时功率

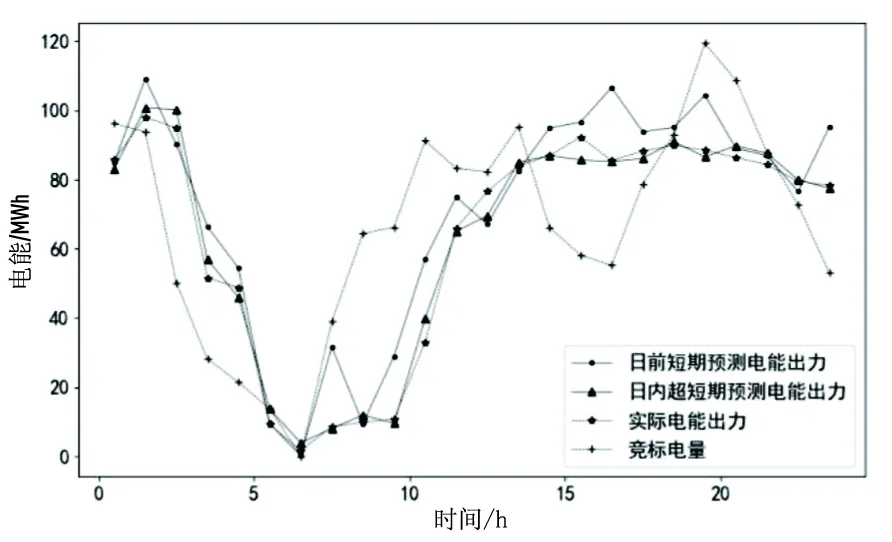
图8 系统电能出力日前预测值、日内预测值、实际值以及竞标电能

日前竞标策略中，2-5时、14-17时和23-24时电价较低，储能系统将一部分电能储存起来；0-1时、8-11时和18-21时电价较高，储能系统放电。可再生能源系统总电能出力为风力发电、光伏发电和储能系统出力之和。由图7可看出，在2-5时和14-18时，竞标电量显著低于系统总电能出力；在8-11时和19-20时，竞标电量显著高于系统总电能出力。这是模型经过大量训练学得的竞标策略，很大程度上降低了因可再生能源出力不确定性而造成的利润损失。

日内实时调度策略得到的储能系统发电计划大部分与日前发电计划相同，但在18-19时，此时不平衡电价为下调电价，系统实际总电能出力大于竞标电量。因此实时调度策略会根据超短期不平衡电价预测值减少储能系统放电量，并在20-21时再放出。

3.3 结果分析

为进一步分析验证所提策略的有效性，在此设置四种策略进行对比分析。

策略1：只考虑日前市场竞标，日前市场竞标值为日前风力发电和光伏发电预测值之和，储能系统不参与日前市场竞标，日内也不进行充放电。

策略2：日前市场竞标值为日前风力发电和光伏发电预测值之和。日内根据超短期风力发电和光伏发电预测值进行储能系统充放电，平衡风电和光电误差。

策略3：只采用该文提出的DDPG算法进行日前市场竞标，不考虑实时能量调度。储能系统参与日前市场竞标，日内储能系统按日前计划进行充放电，即储能系统在低电价时将部分电能储存起来在高电价时卖出。

策略4：采用该文提出的日前竞标策略和日内实时能量调度策略。

若日前市场竞标值为日前风力发电和光伏发电实际值之和，系统每日平均收入为44 527.13欧元。由表5数据可知策略1平均每日因风能和光能预测误差造成的损失为777.57欧元。根据每日超短期风能和光能预测结果，策略2可通过储能系统充放电来减少系统出力实际值与竞标值的误差，系统每日平均收入为43 995.14欧元。策略3每日平均利润为44 802.35欧元。这部分利润可分为两部分，一部分是储能系统在低电价时将部分电能储存起来在高电价时卖出获得的奖励，另一部分是通过竞标获得。

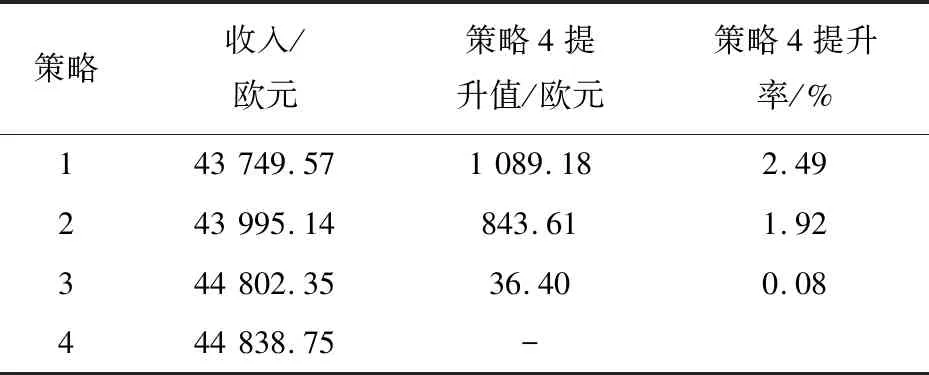
表5 不同策略的收入和策略4的利润提升

策略4每日平均利润为44 838.75欧元。与策略1和策略2相比，策略4平均每日分别增加了1 089.18欧元、843.61欧元的利润，利润提升率分别为2.49%、1.92%。策略4与策略3相比平均每日增加了36.40欧元的利润，提升率为0.08%，日内实时能量调度为系统带来的提升幅度较小。实时能量调度是对储能系统日前发电计划进行调整以减少因系统出力的不确定性而造成的损失，同样地也会造成一部分利润(日前计划储能系统在低电价时存储电能并在高电价时卖出所获得的利润)的减少。因此超短期不平衡电价的预测显得尤为重要。该文采用SARIMA模型对超短期不平衡电价进行预测，平均绝对百分比误差为12.29%，误差较大，因此导致实时能量调度策略带来的利润增幅较小。通过以上对比分析，验证了所提策略能够通过合理调度储能系统充放电过程提升系统的收入。

4 结束语

针对风-光-储可再生能源系统，提出了基于强化学习DDPG算法的日前电力市场竞标-日内实时能量调度策略，并通过实验验证了该策略的有效性。

选取澳大利亚风电场和光伏电场与北欧电力市场608天发电功率数据和电价数据进行模型的训练和验证。经训练得到的智能体能够充分利用蓄电池的灵活性，低电价时充电高电价时放电，同时能够减少不平衡功率，有效降低损失。实验结果显示，与竞标量为电能预测值的简单策略相比，提出的日前市场竞标-日内实时调度策略可提高2.49%的系统收入。

不足之处是日内实时调度策略效果较差，利润提升较少，其原因是不平衡电价的预测不够准确。面向日内平衡市场，若蓄电池的实时调度策略不能有效减少因发电偏差带来的损失，反而会使可再生能源系统获得的利润减少。因此，在后续的研究中将采取更合理的算法对电价进行预测并增加新的强化学习技术来提高日内实时调度模型学习策略的能力。