基于无监督的非对称度量学习优化行人再识别
2022-09-16江雨燕
江雨燕,吕 魏,李 平,邵 金
(1.安徽工业大学 管理科学与工程学院,安徽 马鞍山 243032;2.南京邮电大学 计算机学院,江苏 南京 210023)
0 引 言
行人再识别[1]在于行人从一个相机消失到另一个相机再次出现的时候对其进行再识别。目的是为了判别同一个人出现在两个视图中的相似性。通过度量学习的方法来计算两个视图特征的距离来判断其相似性。在行人再识别算法上也有关于度量学习[2]和深度学习[3]被提出,基于无监督学习的科学技术研究方法通过伪标签的形式进行特征学习可以有效深度学习中改善全局特征不容易轻松识别的问题并能够产生良好的效果。
基于无监督学习的研究方法在面对同样的行人出现在不同摄像机里会因为外在因素,例如光线、姿势以及障碍物等造成两者的相似度降低[4];同时两者也存在衣服、肤色等外在特征相似的地方。但是需要对每个摄像机视图构建映射来提高相似性,并且难以区分共享视图和特定视图,无法准确地建立摄像机视图之间的共同性质和特异性质。因此通过跨视图非对称的方法[2,4-6]把视图特征区分为共享视图特征和特定于视图特征,引入共享映射来探索共享特征,提取特定的视图特征投影到公共子空间中使得两视图之间的差异尽可能缩小,然后通过无监督学习进行聚类[2-3,7]。但是,在特定于视图特征的相似度区分上还需要进一步提高,通过Bregman散度[8]方法来衡量特定于视图之间特征的差异,减少对共享视图特征区分的重复性,提高聚类效果,增强视图之间的相似度,从而提高视图之间相似的精确度。
对不断更新增长的数据进行标签是一项艰难而又复杂的工作,Martin Köstinger等人[9]提出了一种通过等价约束来指定标签,并通过马氏距离度量的可扩展性和需要的监督程度来进行学习,明显优于现有的结果。Husheng Dong等人[10]提出了一种新的基于重叠条纹的描述子与从密集块中提取的局部最大发生率(LOMO)相融合的增强局部最大发生率的方法,把精细的细节和表面的粗糙有效结合起来,充分利用其互补性,结合马氏距离和双线性相似性学习广义相似性。Giuseppe Lisanti等人[11]提出了基于正则化相关分析的跨视图匹配的学习技术,在不相交的视图中提取描述子空间的特征投影到公共子空间进行学习,在重新识别的技术上有明显的效果。Yachuang Feng等人[3]基于度量学习将行人的特征投影到公共子空间中,在公共子空间中将行人的特征提取出来分为共同特征和特定视图特征,并通过无监督跨视图的度量学习方法来计算相似性,通过最大均值差异(MMD)来计算不同样本的均值,常作为最后损失函数的优化,在迁移学习中使用频率相对较高且计算强度低,通常用来衡量两个分布之间的距离,属于一种核学习方法。为缩减样本之间的差异性,该文采用Bregman散度中的KL散度,KL散度在视图中满足非对称特性,增加一个样本的协方差,这样能够在一定程度上提高样本之间的精确度。
1 相关工作
1.1 跨视图非对称度量学习
传统的度量学习是学习一个通用的变换矩阵,并将样本投影到一个公共子空间,一对样本xi和xj的距离为:
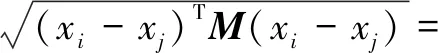
‖Wxi-Wxj‖2
(1)
其中,M=WTW,W是投影矩阵,xi和xj是相机视图中获取的不同样本。由于所有视图中的样本都在(1)中处理相同的W,只从不同的视图中提取共享特征。根据跨视图非对称度量学习,为了处理摄像机视图之间的不相似性,其形式如下:
(2)
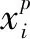
(3)
其中,U0表示共享视图投影,用于提取共同特征,Uv表示特定于视图的投影,把Up和Uq投影到子空间来消除视图之间的特异性。并让Uvxv与U0xv正交,让提取的视图专有特征与普通特征互补。
目标模型:

(4)
这里Wv=U0+Uv,重写目标函数:

(5)
其中,∑v=XvXvT/Nv,I表示单位矩阵。
共享信息为U0,特定于视图信息为Uv。Uv被分为Up和Uq,为了保证Up和Uq学到不同的信息,部分信息不被划分到共享信息里面,这里保持Uv和U0尽量正交,又因为两者属于不同的样本,直接正交没有意义,故使得Uvxv与U0xv正交,这里引入Bregman divergence,通过Bregman divergence来衡量Up和Uq之间的差异。
1.2 Bregman散度
Bregman散度是损失函数或者失真函数,假设视图p是视图q的近似样本,p是增加了障碍物或者光线的影响而形成的q,所以Bregman散度就是用来衡量p和q的之间的差异性。定义F是在凸集Ω上可微的严格凸函数,在函数F生成的Bregman散度的形式是[7]:
DF(p‖q)=F(p)-[F(q)+
(6)
其中,DF(p,q)表示样本p与q之间的距离,用来衡量p与q之间的差异,F(q)表示在q的梯度,
假设来自不同视图的样本是从类似场景中捕获,因此它们的概率分布被视为相同。但在原始特征空间中的分布通常是不同的,因为它们是从不同的相机、不同的场景中捕获的,直接计算它们的距离可能是不准确的。为此,尽可能地提高它们在变换后的子空间中的概率分布的相似性,选择不同的函数F,采用KL散度来衡量样本分布之间的差异性。KL散度能够有效解决样本之间非对称的问题,并且在衡量样本之间差异性的时候,能够有效衡量样本的近似分布与真实分布之间的匹配程度,主要通过计算两个样本之间的高斯分布来表示KL散度。这里计算Up和Uq之间的距离形式为:
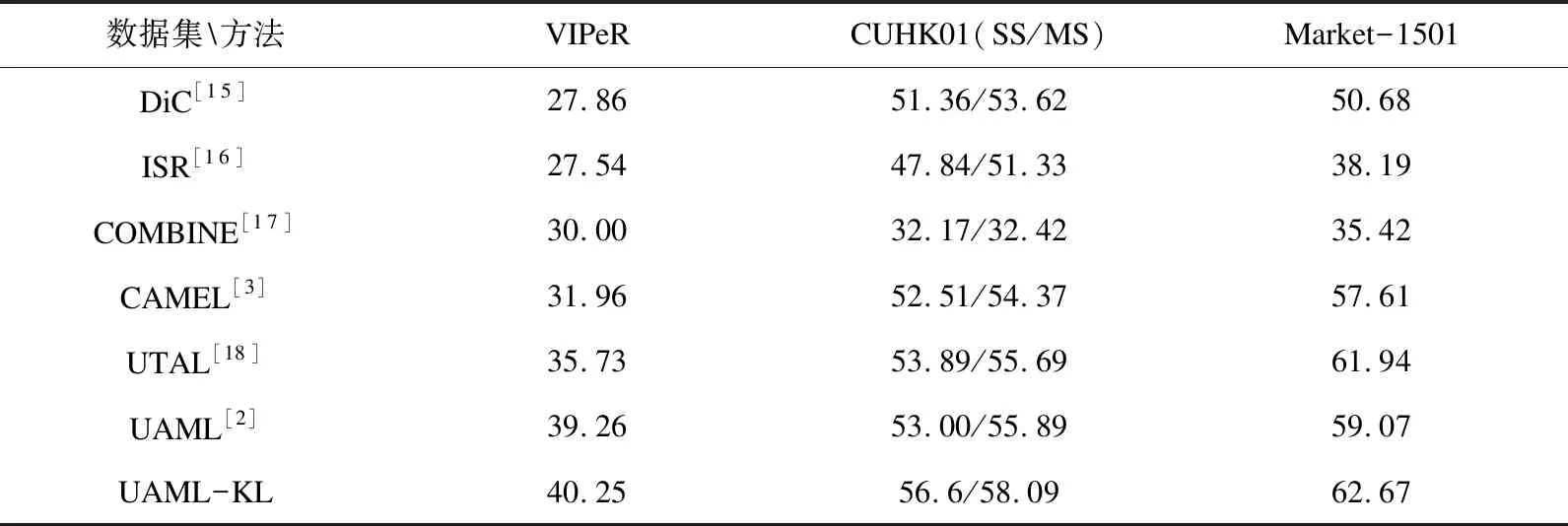
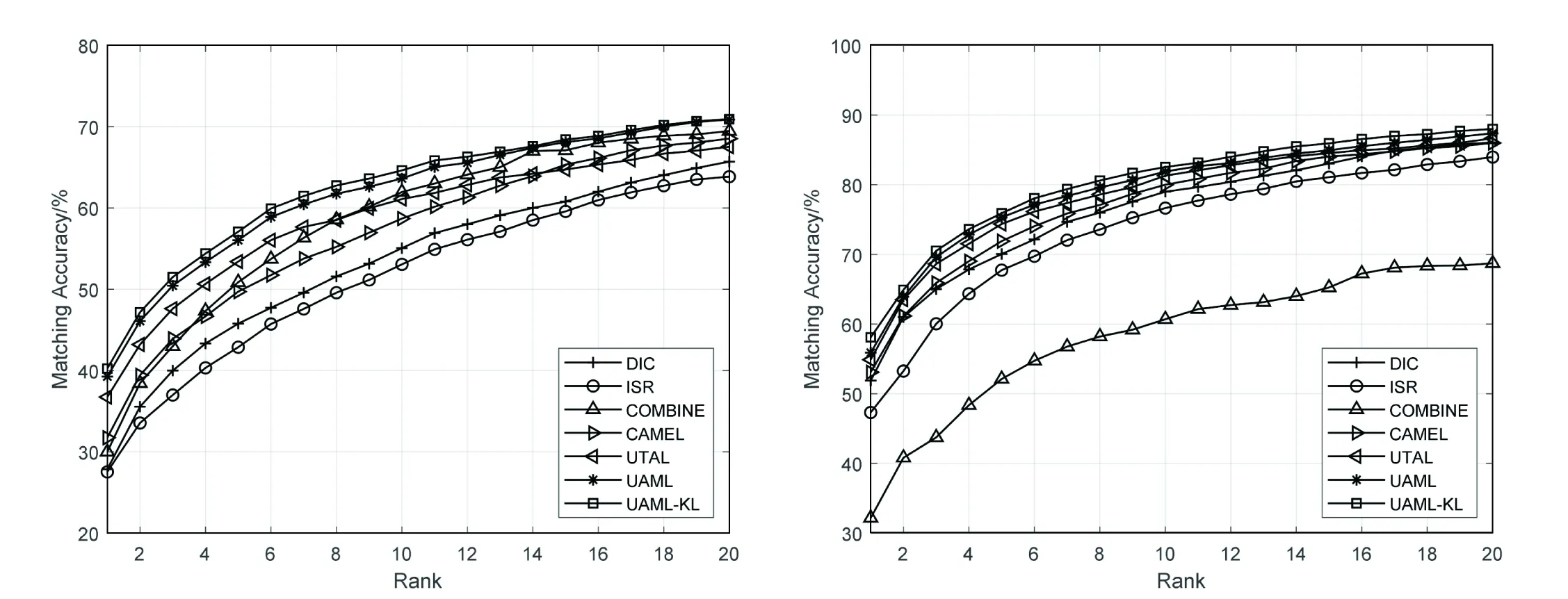
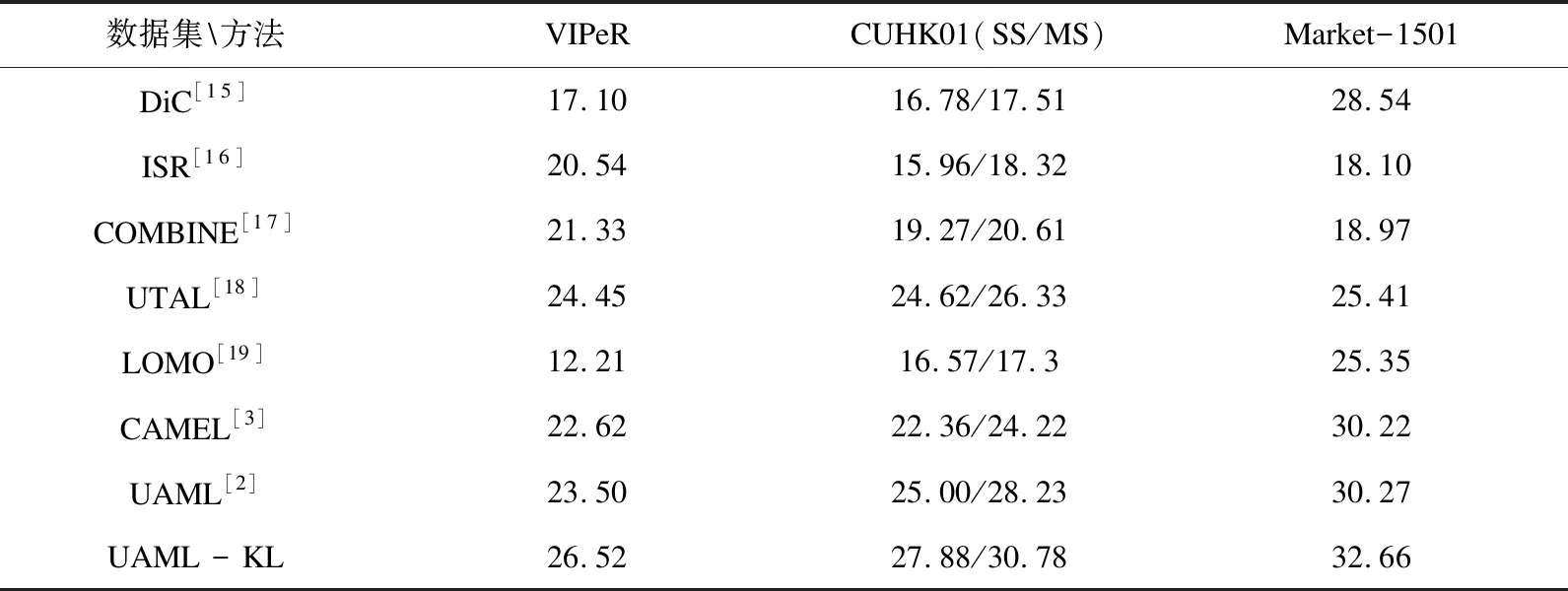
DF(Up‖Uq)=F(Up)-[F(Uq)+ Up-Uq>] (7) KL散度的形式为KL(p(hp)‖p(hq)),其中p(hv)~N(μv,Hv),p(Uv)是服从均值为μv,协方差为Hv的多元高斯分布,Up和Uq的多元高斯分布p(hv)表示为: (hv-μv)T(Hv)-1(hv-μv)] minO(U0,…,Uv)= (UvT∑vUv=I),V=1,2,…,v (8) 算法:跨视图非对称度量学习的行人重识别 1.通过K均值使用原始训练数据X来初始化D 3.重复: 6.直到收敛或迭代结束 (9) 对两个高斯分布p(hp)~N(μp,Hp),p(hq)~N(μq,Hq)计算KL散度KL(p(hp)‖p(hq))为:KL(p(hp)‖p(hq))=Epl(lnp(hp)-lnp(hq))即: (10) Bregman散度中的KL散度计算样本均值,还计算了样本的协方差,因此与最大均值误差(MMD)方法进行比较,这两种方法均可以对不同的分布进行判断,并且满足不同分布的距离不对称性。 放宽约束条件: (11) minO(U0,…,UV)= (13) 对C进行k-means聚类优化,然后再计算D。 (14) (15) 其中K的形式为: (16) 这里A、B、L分别表示如下: (17) (18) L=(μqT+μpT)Hq-1AHq-1μp+(μpT- (19) (20) (21) 取所有等式右侧函数的平方和为目标函数,计算这个函数关于自变量UV以和乘子Ψ、φ偏导数,再对关于自变量及乘子的偏导数进行迭代求解。 通过数据样本来训练该方法的有效性,使用Cumulative Match Characteristic (CMC) Curve累计匹配曲线能够综合反映分类器的性能,Rank-1精度通过百分比的形式,计算每百张的平均精确度对文中方法和其他方法进行比较。 VIPeR[12]数据集(见图1)通过随机将其分为两半,316张图像用于训练,316张图像用于测试。重复这个过程十次,并报告每个算法的平均性能进行比较。 图1 VIPeR数据集部分行人样本 CUHK01[13](见图2)是通过两个不重叠的摄像机捕捉的971个行人身份视图,每视图有4个图像,共有3 884个图像。训练集随机选择485人,测试集为其余486对行人。通过十次重复来评估并同时进行单镜头(SS)和多镜头(MS)实验。 图2 CUHK01数据集部分行人样本 Market-1501[14](见图3)与其他的数据集不同,只能在多镜头上进行实验。选择751人作为训练集,共12 936张图像,其余750人用于测试。 图3 Market-1501数据集部分行人样本 这里主要是与稀疏字典学习模型(简称Dic)[15]、稀疏表示学习模型(ISR)[16]、视跨图非对称度量学习(CAMEL)[3]、组合度量(COMBINE)[17]、无监督轨迹(UTAL)[18]、无监督的跨视图度量学习(UAML)[2]进行比较,如表1所示,并画出CMC曲线,如图4所示。 表1 用秩-1精度(%)和MAP(%)测量三个数据集的无监督方法的比较结果 UAML - KL通过学习每个摄像机视图的投影矩阵,不仅把投影矩阵划分成了共享投影和特定于视图的投影去学习特征,在计算样本的分布差异过程中引入了KL散度,通过计算两者的多元高斯分布来表示分布的KL散度,进一步去加强再识别的精度值,探索共同的特性并降低视图之间的不一致之外,还更加细化每个摄像机视图的特定视图的特征。 (a)VIPeR (b)CUHK01(SS) 3.3.1 共享映射和特定视图映射分析 共享映射和特定视图映射的作用主要是对摄像机视图之间的共性与不一致性进行建模来获得比较全面的、具有区分性的行人特征。为了使得该方法具有一定的性能,通过控制共享特征和特定于视图的特征,只保留U0或UV来进行对比验证,如表2所示。 表2 非对称度量学习验证 KL散度的非对称性质能够很好地与非对称度量学习相契合,通过均值和协方差,在衡量样本分布的时候,能够与真实样本分布进行匹配,匹配程度越高,则样本分布愈接近真实的样本分布,进一步改善相机视图之间的分布差异。除了特定于视图的映射可以为共享的特性提供互补的信息之外,还构建了全面的和有区别的表示。 3.3.2 聚类分析 在三个数据集上验证K对行人再识别性能的影响实验。结果如表3所示,K在200到1 600之间变化,时间间隔为200。CUHK01的性能变化较大,这是因为CUHK01与Market相对较小的集群。过多或过少的集群可能会阻碍对行人的样本之间关系的准确探索。 表3 不同聚类中心数量结果 3.3.3 特征分析 为了适应不同特征的能力,为证明不仅在采用基于深度学习的JSTL特性时也很有效,还采用了LOMO特征,先进行PCA进行降维,得到512维LOMO特征,如表4所示。在所有模型中,Dic和ISR的结果最具可比性(Dic和ISR位居第二)。所以为了清晰起见,只把该方法和其他特征提取方法比较,LOMO特征作为基线。 表4 使用LOMO特征的比较结果 无监督的行人再识别度量学习方法的基本思想是每个摄像机视图中的行人样本分别是从两个分布中提取的:一个提取的是摄像机视图之间的共同特征,另一个提取的是特定于视图的特征。引入一个共享映射来探索共享特征,并构造特定于视图的映射与视图相关的特征提取投影到一个公共子空间中。这样不仅降低相机视图之间的不一致性,还更加细化了特定视图的特征,能够更加精确地对行人进行再识别。此外,为了实现精确的相似性测量,还减少变换空间中摄像机视图之间的分布差异,在投影空间中对样本进行聚类,通过无监督的方式进行优化。实验结果表明,与其他算法相比,该方法具有较好的性能。2 模型与优化
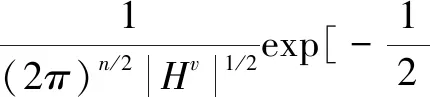

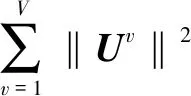


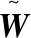

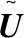

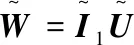
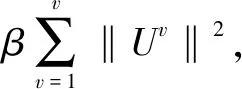

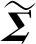




3 实 验
3.1 数据集介绍



3.2 参数设置

3.3 结果分析


4 结束语
